动态规划
dp
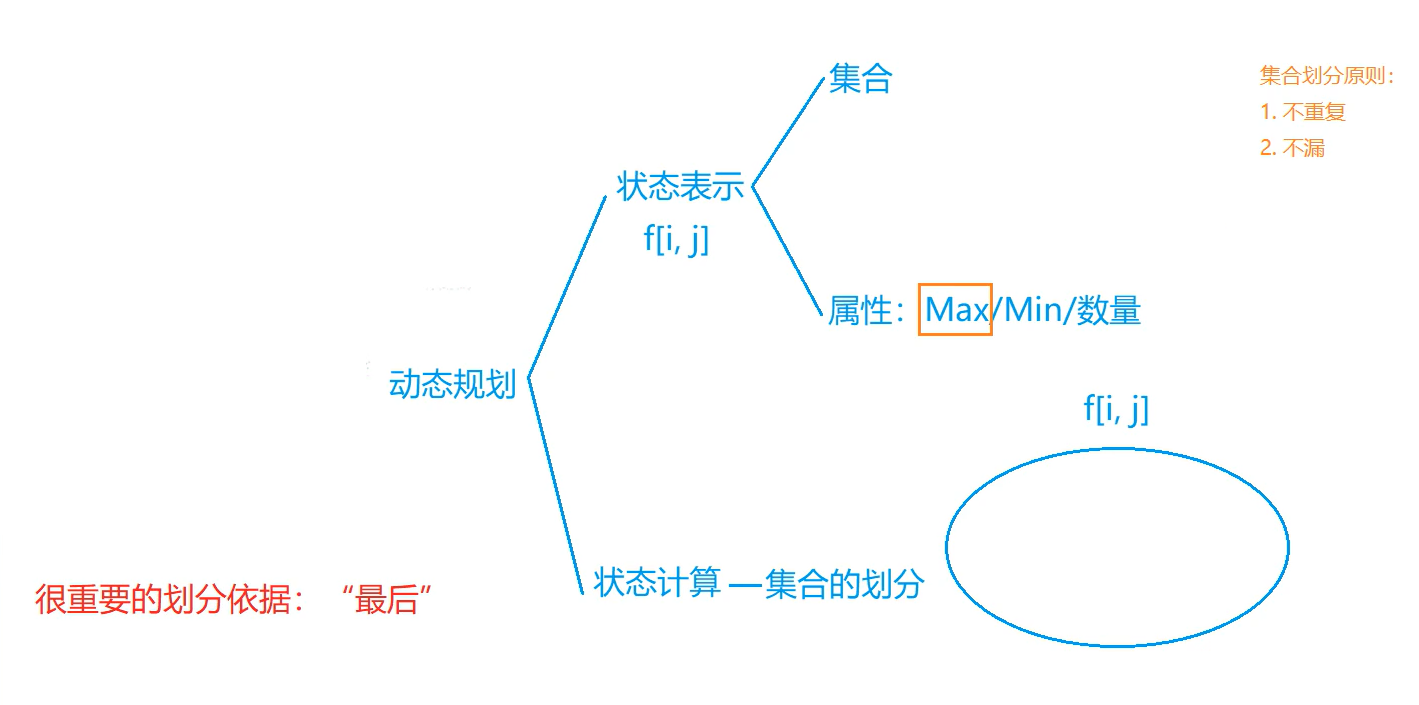
数字三角形
例题1:
题意:
从(1,1)到(r,c)摘花生,不可走回头路,最多可以摘多少
思路:
f[i, j]:(1,1)到(i,j)的最大摘花生数
核心代码:
for(int i = 1; i <= r; i++) { for(int j = 1; j <= c; j++) { f[i][j] = max(f[i - 1][j], f[i][j - 1]) + a[i][j]; } } cout << f[r][c] <<'\n';
例题2
题意:
从(1,1)到(n,n)在每一个方格中取数,方格中数被取后数变成0,可走两次,问可取最大数为几
思路:
用两次dp无法确定是否是最优解
用f[i1][j1][i2][j2]表示从(1,1)开始同时走分别走到(i1,j1)(i2,j2)的最大取数
i1+j1=i2+j2时才是同时走的
设k = i1+j1
用三维dp,f[k][i1][i2]求解(横纵坐标和为k时,纵坐标走的i1,i2的时候,最大取数)
核心代码:
for (int k = 2; k <= n + n; k ++ ) for (int i1 = 1; i1 <= n; i1 ++ ) for (int i2 = 1; i2 <= n; i2 ++ ) { int j1 = k - i1, j2 = k - i2; if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n) { int t = w[i1][j1]; if (i1 != i2) t += w[i2][j2]; int &x = f[k][i1][i2]; x = max(x, f[k - 1][i1 - 1][i2 - 1] + t); x = max(x, f[k - 1][i1 - 1][i2] + t); x = max(x, f[k - 1][i1][i2 - 1] + t); x = max(x, f[k - 1][i1][i2] + t); } } printf("%d\n", f[n + n][n][n]);
最长上升子序列(LIS)
例题1
f[i] :所有以a[i]结尾的单调上升子序列长度最大值
核心代码:
for(int i = 1; i <= n; i++) { f[i] = 1; for(int j = 1; j < i; j++) { if(a[i] > a[j]) f[i] = max(f[i], f[j] + 1); } } int ans = 0; for(int i = 1; i <= n; i++) { ans = max(ans, f[i]); } printf("%d", ans);
例题2
题意:
输入一个长度为n的序列,可以从1~n任意位置做起点,可以向左或向右走,求最长子序列长度(向左走求最长上升子序列长度 eg:12345,向右走求最长下降子序列长度 eg: 54321)
思路:
两个数组分别存向左/向右的长度,求Max
核心代码:
for(int i = 1; i <= n; i++) { rf[i] = 1; for(int j = 1; j < i; j++) { if(a[i] < a[j]) rf[i] = max(rf[i] , rf[j] + 1); } } for(int i = n; i >= 1; i--) { lf[i] = 1; for(int j = n; j > i; j--) { if(a[i] < a[j]) lf[i] = max(lf[i] , lf[j] + 1); } } for(int i = 1; i <= n; i++) ans = max(rf[i], max(ans, lf[i])); cout << ans << '\n';
例题3
题意:
给定景点编号,进行观光,要求:按照顺序给定顺序递增浏览,相邻两个景点不能相同,一旦开始下降了就不能上升了
思路:
求出如上题的rf[i], lf[i],将第i位上的rf[i] 与 lf[i]相加,求Max
核心代码:
for(int i = 1; i <= n; i++) { f[i] = 1; for(int j = 1; j < i; j++) { if(a[j] < a[i]) f[i] = max(f[i], f[j] + 1); } } for(int i = n; i >= 1; i--) { g[i] = 1; for(int j = n; j > i; j--) { if(a[j] < a[i]) g[i] = max(g[i], g[j] + 1); } } for(int i = 1; i <= n; i++) ans = max(ans, f[i] + g[i] - 1);
例题4
题意:
河对岸各有一些城市,给两岸的城市建桥,问最多可以建多少桥?
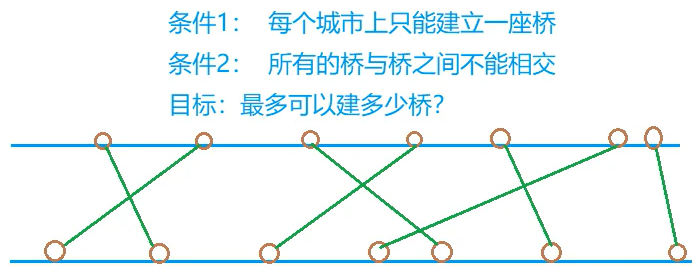
思路:
排序后求LIS
核心代码:
for(int i = 1; i <= n; i++) cin >> town[i].a >> town[i].b; sort(town+1, town+n+1, cmp); for(int i = 1; i <= n; i++) { f[i] = 1; for(int j = 1; j < i; j++) { if(town[j].b < town[i].b) f[i] = max(f[i], f[j] + 1); } } for(int i = 1; i <= n; i++) ans = max(f[i], ans); cout << ans;
例题5
题意:
有一系列导弹,现在要用导弹系统拦截,每套导弹系统拦截导弹高度只能不断向下
第一问:每套导弹拦截系统拦截导弹高度为下降子序列,求最长的就好了
第二问:求导弹拦截系统的个数可以转化为求最长上升子序列长度
思路:
第一问:参考例题1,上升变为下降
第二问:用不同序列来存贮导弹高度,满足以下条件
1.如果现有子序列结尾小于当前数,创建新子序列
2.当前的数放到大于等于他的最小的子序列后面
序列数为答案
核心代码
for(int i = 0; i < n; i++) { f[i] = 1; for(int j = 0; j < i; j++) { if(a[j] >= a[i]) f[i] = max(f[i], f[j] + 1); } res = max(res, f[i]); } cout << res << '\n'; int cnt = 0; for(int i = 0; i < n; i++) { int k = 0; while(k < cnt && g[k] < a[i]) k++; g[k] = a[i];//g[k]存贮每一序列的最后一个数 if(k >= cnt) cnt++;//开启新序列 } cout << cnt << '\n';
例题6
题意:
题目给定一个长度为 n 的数组 w[n] ,要求我们用最少的上升子序列和下降子序列完全覆盖该数组
求该方案的上升子序列和下降子序列的总个数
思路:
最核心的思想在于能否将一个元素加入到序列中,只与这个序列目前的最后一个元素有关
这道题就用了这个关键的思想。
用up[k]和down[k]记录第k套上升(下降)系统目前所拦截的最后一个导弹
dfs(u,v,t)意味着已有u个上升,v个下降,正在处理第t个数
是例题5的扩展
代码:
#include<iostream> using namespace std; const int N = 60; int n; int h[N]; int ans; int up[N], down[N]; void dfs(int u, int su, int sd)//当前导弹编号 ,上升序列个数 ,下降序列个数 { if(su+sd >= ans)//无法出现更优解减枝 return; if(u == n){ if(su + sd < ans)ans = su + sd;//出现更优解,更新 return; } int k = 0; //上升子序列 while(k < su && up[k] >= h[u]) k++; if(k < su)//放入一个已有子序列中 { int tem = up[k]; up[k] = h[u]; dfs(u+1, su, sd); up[k] = tem; }else{//开一个新序列 up[k] = h[u]; dfs(u+1, su+1, sd); } //下降子序列 k = 0; while(k < sd && down[k] <= h[u]) k++; if(k < sd) { int tem = down[k]; down[k] = h[u]; dfs(u+1, su, sd); down[k] = tem; }else{ down[k] = h[u]; dfs(u+1, su, sd+1); } } int main() { while(cin >> n, n) { for(int i = 0; i < n; i++) scanf("%d", &h[i]); ans = n; dfs(0 ,0 ,0); cout << ans << '\n'; } return 0; }
例题7
题面:
求最长公共上升子序列长度
思路:
f[i,j]分为两种:
1.所有不包含a[i]的公共上升子序列f[i,j] =
2.所有包含a[i]的公共上升子序列,根据a[i]与b中哪一个数相同来计算
有f[i,k]+1
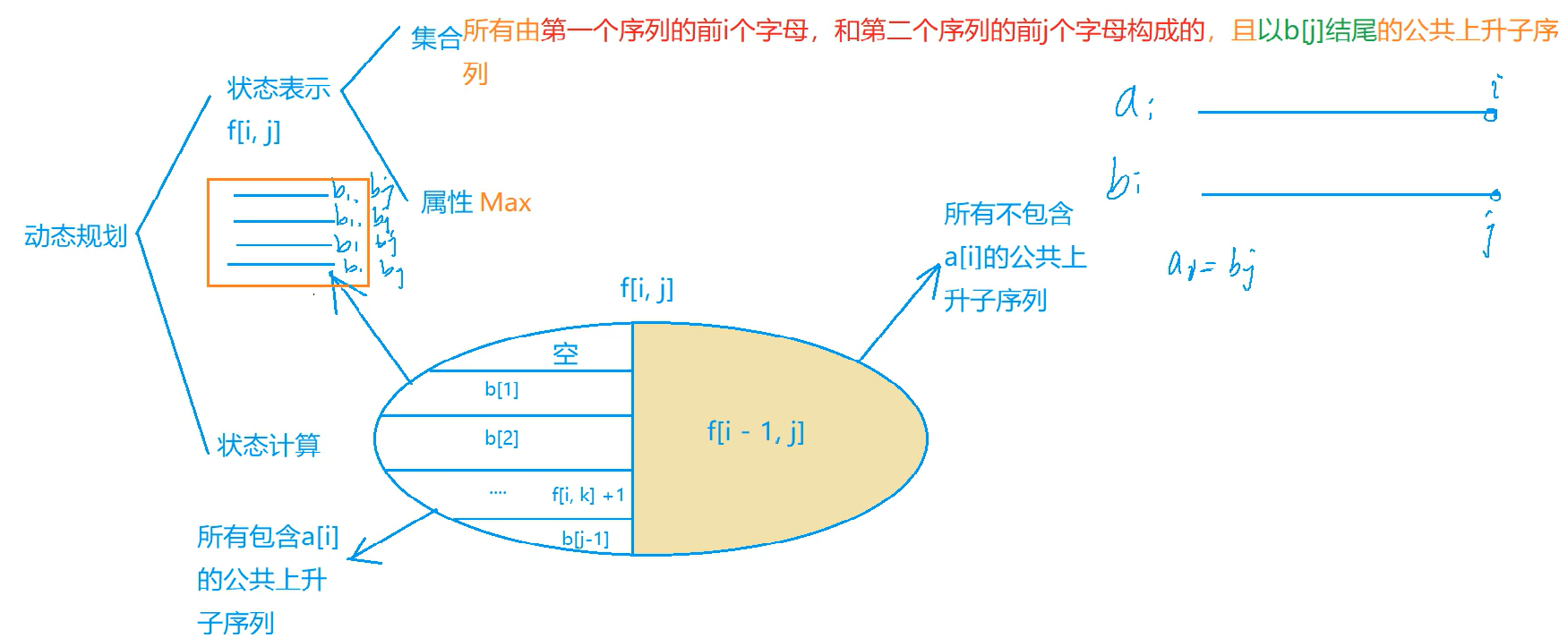
代码:
for (int i = 1; i <= n; ++ i) { for (int j = 1; j <= n; ++ j) { f[i][j] = f[i - 1][j];//先考虑右边情况 if (a[i] == b[j])//考虑左边情况 { for (int k = 0; k < j; ++ k) { if (b[j] > b[k]) { f[i][j] = max(f[i][j], f[i - 1][k] + 1); } } } } } int res = 0; for (int i = 0; i <= n; ++ i) res = max(res, f[n][i]); cout << res << '\n';
代码优化:
for (int i = 1; i <= n; ++ i) { int maxv = 1; for (int j = 1; j <= n; ++ j) { f[i][j] = f[i - 1][j]; if (b[j] == a[i]) f[i][j] = max(f[i][j], maxv); if (b[j] < a[i]) maxv = max(maxv, f[i][j] + 1); } }
背包问题
01背包:
每个物品个数为1,对于他只有选与不选两种状态

f[i, j]表示只从前i个物品里面选,总体积小于等于j的方案数
二维代码:
#include <iostream> #include<cmath> using namespace std; int f[1010][1010]; int v[1010]; int w[1010]; int main() { int n, m; cin >> n >> m; for(int i = 1; i <= n; i++) { cin >> v[i] >> w[i]; } for (int i = 1; i <= n; i++)//枚举所有物体 { for (int j = 0; j <= m; j++)//枚举所有体积 { f[i][j] = f[i - 1][j];//上一个物品不选这个方案一定是可以存在的 if (j >= v[i]) //这一步目为了取上一次选与不选中的最大值 { //max()内的f[i][j]相当于f[i-1][j] f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); } } } printf("%d", f[n][m]); return 0; }
代码优化:
通过观察状态转移方程:f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
我们可以发现 f 的第一维只有 i 与 i-1, 没有 i-2 ,i-3 .....可以考虑使用滚动数组
我们尝试去掉 f 的第一维
优化思路
for (int i = 1; i <= n; i++) { for (int j = v[i]; j <= m; j++) { //f[j] = [j];一个等式省略不写 //if (j >= v[i]) //可以放在for循环条件内 //{
// j-v[i] < j 所以 j 遍历的时候,这一层的 j-v[i]必定已经被遍历过,此时的 f[j - v[i]] 表示的是 f[i][j - v[i]]]
//所以对j的枚举要从大到小
f[i] = max(f[j], f[j - v[i]] + w[i]);
//f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); //} } }
优化后代码:
for (int i = 1; i <= n; i++) { for (int j = m; j >= v[i]; j--) { f[j] = max(f[j], f[j]-v[i]] + w[i]); } }
二维01背包
题目:
代码:
#include <iostream> #include <algorithm> using namespace std; const int N = 1010, M = 110; int f[N][N]; int v[N]; int g[N]; int w[N]; int main() { int n ,V, m; cin >> n >> V >> m; for(int i = 1; i <= n; i++) { cin >> v[i] >> g[i] >> w[i]; } for(int i = 1; i <= n; i++)//个数 { for(int j = m; j >= g[i]; j--)//重量 { for(int h = V; h >= v[i]; h--)//体积 { f[j][h] = max(f[j][h], f[j-g[i]][h-v[i]]+w[i]); } } } cout << f[m][V]; return 0; }
完全背包
每个物品有 k 个
f[i, j] 表示只考虑前i个物品(物品可选0~k个)且体积不大于 j 的选法
对于 f[i, j] 我们选取 f[i-1][] 层时,我们对选 0~k 个物品选取其中最大值
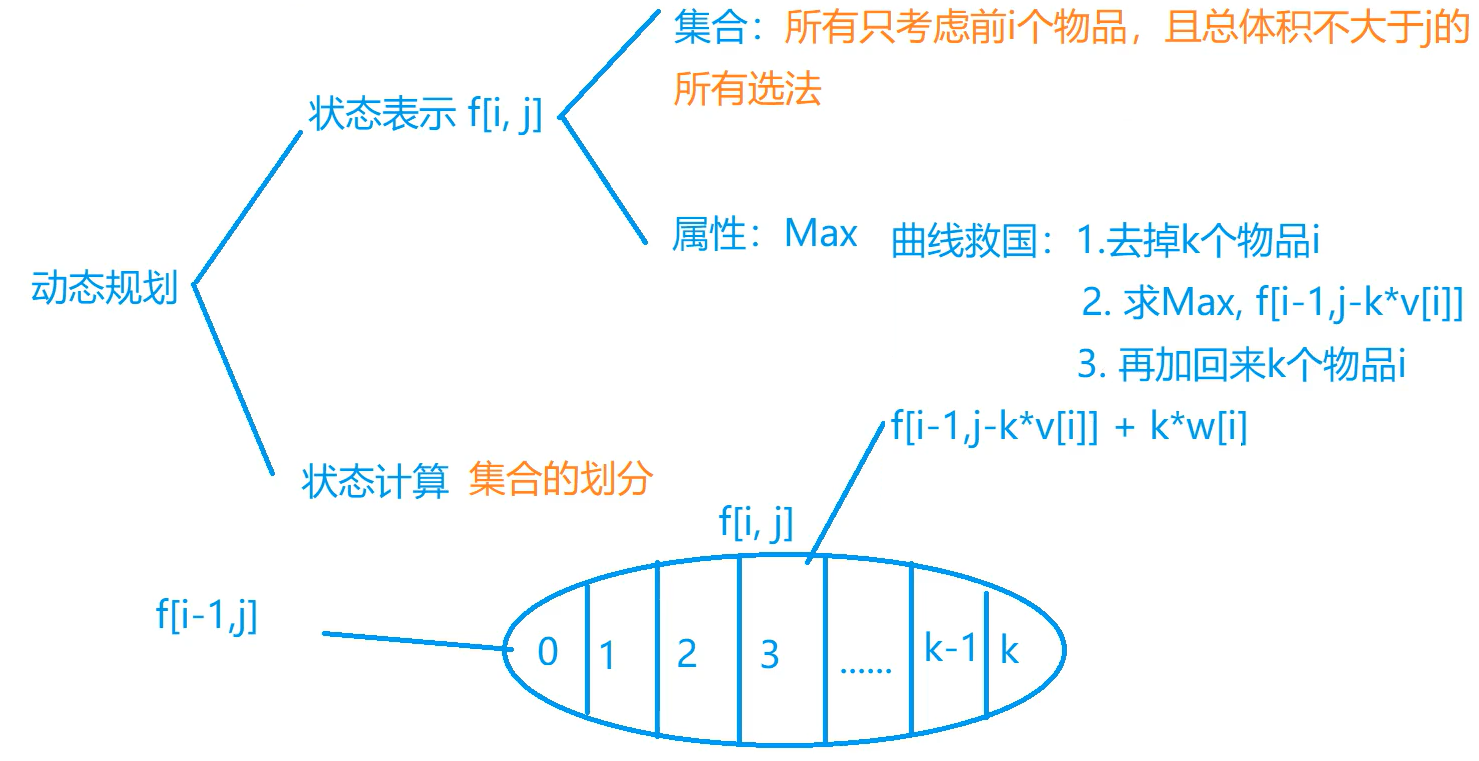
朴素写法
for (int i = 1; i <= n; i++) { for (int j = 0; j <= m; j++) { for (int k = 0; k * v[i] <= j; k++) f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]); } }
优化思路
f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....) f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....)
发现
f[i, j] = max(f[i-1,j], f[i , j-v]+W);
由此发现可以去掉循环中的 k
优化后代码:
for (int i = 1; i <= n; i++) { for (int j = 0; j <= m; j++) { f[i][j] = f[i - 1][j]; if (j - v[i] >= 0) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]); } }
01背包与完全背包区别
![]()
多重背包
对于每个物品个数有 Si 限制
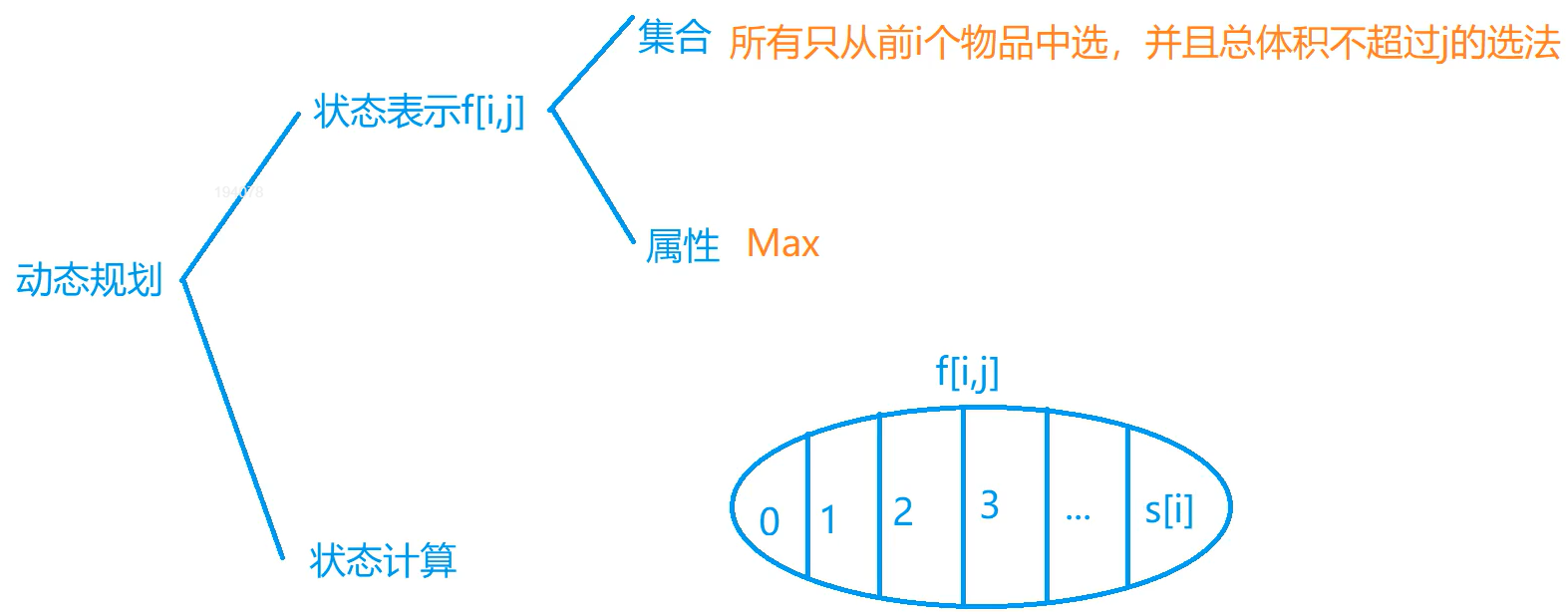
朴素版本与完全背包问题类似
for(int i = 1; i <= n; i ++){//枚举背包 for(int j = 1; j <= m; j ++){//枚举体积 for(int k = 0; k <= s[i]; k ++){ if(j >= k * v[i]){ f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]); } } } }
二进制优化:
对于任意一个十进制,我们都可以用几个二进制数来表示,所以对于某一个数。我们可以优化为一些二进制数的选与不选(01背包问题)
代码:
//将每种物品根据物件个数进行打包 int cnt = 0; for(int i = 1; i <= n; i ++){ int a, b, s; cin >> a >> b >> s;//体积、价值和数量 int k = 1;//用来表示2的几次方 while(k <= s){ cnt ++; v[cnt] = k * a; w[cnt] = k * b; s -= k; k *= 2; } if(s > 0){ cnt ++; v[cnt] = s * a; w[cnt] = s * b; } } //多重背包转化为01背包问题 for(int i = 1; i <= cnt; i ++){ for(int j = m; j >= v[i]; j --){ f[j] = max(f[j], f[j - v[i]] + w[i]); } } cout << f[m] << '\n';
分组背包:
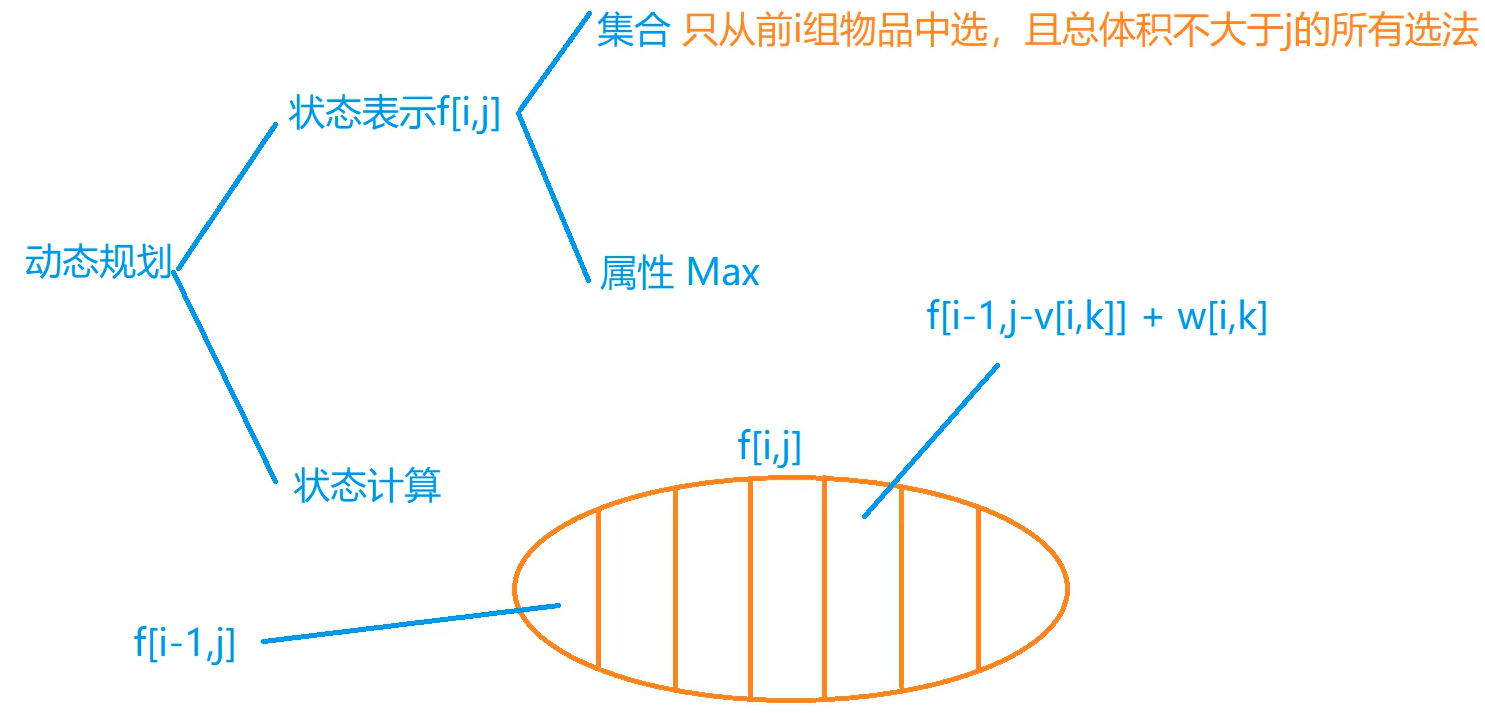
对于只选前 i 组物品,且体积不超过 j 的方案数
v[i, k] 第 i 组物品的第 k 个物品
int n, m; //输入物品组数与背包容量 scanf("%d%d", &n, &m); for (int i = 1; i <= n; i++) { int s; scanf("%d", &s); //输入第i个物品组的物品数量 for (int j = 1; j <= s; j++) scanf("%d%d", &v[j], &w[j]); //输入每个物品的体积和价值 //接下来是处理过程 for (int j = m + 1; j >= 1; j--) //枚举所有体积 for (int k = 1; k <= s; k++) //枚举所有选择 if (j >= v[k]) //必须要满足,否则下面的下标减出来是负数 f[j] = max(f[j] /*不选*/, f[j - v[k]] + w[k] /*选*/); } printf("%d", f[m]);
状态机:
找到入口出口,状态转移情况
例题1:
思路:
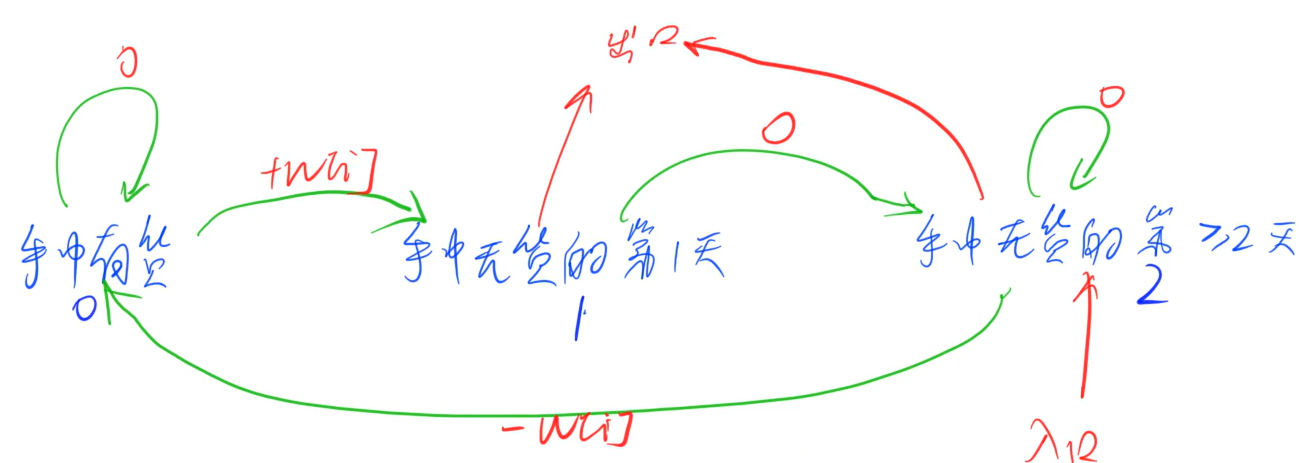
代码:
#include <cstring> #include <iostream> #include <algorithm> using namespace std; const int N = 100010, INF = 0x3f3f3f3f; int n; int w[N]; int f[N][3]; int main() { scanf("%d", &n); for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]); f[0][0] = f[0][1] = -INF, f[0][2] = 0; for (int i = 1; i <= n; i ++ ) { f[i][0] = max(f[i - 1][0], f[i - 1][2] - w[i]); f[i][1] = f[i - 1][0] + w[i]; f[i][2] = max(f[i - 1][2], f[i - 1][1]); } printf("%d\n", max(f[n][1], f[n][2])); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号