树状数组与线段树

树状数组

判断是否用树状数组方法： 是不是只有以下两种操作：

1.修改某一个数字（在某个位置上加一个数来实现）（logn）

2.求前缀和（logn）（区间查询）

求[L,R], 用[1,R]-[1, L-1] c[x] 层数如何定义？

看x的二进制表示最后有k个0

核心代码：

int lowbit(int x)
{
    return x&-x;
}

void add(int idx, int v)//修改
{
    for(int i = idx; i <= n; i += lowbit(i))
        tr[i] += v;
}

int quary(int x)//查询
{
    int res = 0;
    for(int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

 例题：

Acwing.1265

天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。

如果一个星星的左下方（包含正左和正下）有 k 颗星星，就说这颗星星是 kk 级的。

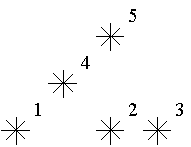
例如，上图中星星 5 是 3 级的（1,2,4 在它左下），星星 2,4 是 1 级的。

例图中有 1 个 0 级，2 个 1 级，1 个 2 级，1 个 3 级的星星。

给定星星的位置，输出各级星星的数目。

换句话说，给定 N 个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

代码：

#include<cstdio>
using namespace std;
const int N = 32000 + 10;
int n, m;
int tr[N];
int level[N];
int lowbit(int x)
{
    return x&-x;
}

void add(int idx)
{
    for(int i = idx; i < N; i += lowbit(i))
        tr[i] ++;
}

int quary(int x)
{
    int res = 0;
    for(int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}
int main()
{
    scanf("%d", &n);

    for(int i = 1; i <= n; i++)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        x++;//为了防止出现0的情况，给它全体横坐标加上 1 就好了。
        level[quary(x)]++;//先查询，在加入当前的点，否则会把当前点也算入
        add(x);
        
    }
    
    for(int i = 0; i < n; i++)
        printf("%d\n", level[i]);

    return 0;
}

 

线段树：

求和：

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 100000+10;

int w[N];
struct node{
    int l, r;
    int sum;
}tr[4*N];

void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void build(int u, int l, int r)
{
    if(l == r){
        tr[u] = {l, r, w[l]};//这一点得值为当前叶子结点得值
    }else{
        tr[u] = {l, r};
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid+1, r);
        pushup(u);
    }

}

void modify(int u, int x, int v)
{
    if(tr[u].l == tr[u].r) tr[u].sum += v;
    else{
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v); 
        pushup(u);
    }
   
}

int quary(int u, int a, int b)
{
    if(a <= tr[u].l && tr[u].r <= b) return tr[u].sum;
    else{
        int sum = 0;
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(a <= mid) sum = quary(u << 1, a, b);//有一段所求在左子树上
        if(mid < b) sum += quary(u << 1 | 1, a, b);//注意后两个空写a，b
        return sum;
    }
}

int main()
{
    int n, m;
    cin >> n >> m;

    for(int i = 1; i <= n; i++) cin >> w[i];

    build(1, 1, n);

    while(m--)
    {
        int k, a, b;
        cin >> k >> a >> b;

        if(k){
            modify(1, a, b);

        }else{
            cout << quary(1, a, b) << '\n';
        }
    }

    return 0;
}