图论
最小生成树
朴素prim
dist[i] 赋值 INF
for(i = 0; i < n; i++)
{
每次找到集合外距离最近的点 t,用 t 更新其他点到集合的距离
st[ t ] = true
}
#include <iostream> #include <cstring> #include <algorithm> using namespace std; const int N = 500+10, INF = 0x3f3f3f3f; int n, m; int g[N][N]; int dist[N]; bool st[N]; int prim() { int ans = 0; memset(dist, 0x3f, sizeof dist); for(int i = 0; i < n; i++) { int t = -1; for(int j = 1; j <= n; j++) { if(!st[j] && (t == -1 || dist[t] > dist[j])) { t = j; } } if(i && (dist[t] == INF)) return INF; if(i) ans += dist[t]; st[t] = true; for(int j = 1; j <= n; j++) dist[j] = min(dist[j], g[t][j]); } return ans; } int main() { memset(g, 0x3f, sizeof g); cin >> n >> m; while(m--) { int a, b, c; cin >> a >> b >> c; g[a][b] = g[b][a] = min(g[a][b], c); } int ans = prim(); if(ans == INF) cout << "impossible\n"; else cout << ans << '\n'; return 0; }
克鲁斯卡尔
1.将所有边按权重从小到大排序 O(mlog(m))
2.枚举每一条边 a , b 与权重 c O(m)
如果 a , b 不连通
将这条边加入集合中去
做部分也是正确的
#include <iostream> #include <cstring> #include <algorithm> using namespace std; const int N = 1e5+10, INF = 0x3f3f3f3f; int n, m; int dist[N]; int p[N]; bool st[N]; struct node { int a, b; int w; }g[2*N]; bool cmp(node x, node y) { return x.w < y.w; } int find(int x) { if(x != p[x]) p[x] = find(p[x]); return p[x]; } int kru() { int cnt = 0, ans = 0; for(int i = 1; i <= m; i++) { int a = g[i].a, b = g[i].b; int fa = find(a), fb = find(b); if(fa != fb) { ans += g[i].w; p[fa] = fb; cnt++; } } if(cnt < n-1) return INF; return ans; } int main() { cin >> n >> m; for(int i = 1; i <= n; i++) p[i] = i; for(int i = 1; i <= m; i++) cin >> g[i].a >> g[i].b >> g[i].w; sort(g+1, g+1+m, cmp); int ans = kru(); if(ans == INF) cout << "impossible\n"; else cout << ans << '\n'; return 0; }
最短路算法
最短路算法分为两大类:
1.单源最短路,常用算法有:
(1) dijkstra,只有所有边的权值为正时才可以使用。在稠密图上的时间复杂度是 O(n2),稀疏图上的时间复杂度是 O(mlogn)。
(2) spfa,不论边权是正的还是负的,都可以做。算法平均时间复杂度是 O(km),k 是常数。 强烈推荐该算法。
2.多源最短路,一般用floyd算法。代码很短,三重循环,时间复杂度是 O(n3)。
算法模板
我们以 poj2387 Til the Cows Come Home 题目为例,给出上述所有算法的模板。
题目大意
给一张无向图,n 个点 m 条边,求从1号点到 n 号点的最短路径。
输入中可能包含重边。
dijkstra算法
时间复杂度O(n2)
基于贪心
最裸的dijkstra算法,不用堆优化。每次暴力循环找距离最近的点。
只能处理边权为正数的问题。
图用邻接矩阵存储。
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int N = 1010, M = 2000010, INF = 1000000000; int n, m; int g[N][N], dist[N]; // g[][]存储图的邻接矩阵, dist[]表示每个点到起点的距离 bool st[N]; // 存储每个点的最短距离是否已确定 void dijkstra() { for (int i = 1; i <= n; i++) dist[i] = INF; dist[1] = 0; for (int i = 0; i < n; i++) { int id, mind = INF; for (int j = 1; j <= n; j++) if (!st[j] && dist[j] < mind) { mind = dist[j]; id = j; } st[id] = 1; for (int j = 1; j <= n; j++) dist[j] = min(dist[j], dist[id] + g[id][j]); } } int main() { cin >> m >> n; for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) g[i][j] = INF; for (int i = 0; i < m; i++) { int a, b, c; cin >> a >> b >> c; g[a][b] = g[b][a] = min(g[a][b], c); } dijkstra(); cout << dist[n] << endl; return 0; }
dijkstra+heap优化 O(mlogn)
用堆维护所有点到起点的距离。时间复杂度是 O(mlogn)。
这里我们可以手写堆,可以支持对堆中元素的修改操作,堆中元素个数不会超过 n。也可以直接使用STL中的priority_queue,但不能支持对堆中元素的修改,不过我们可以将所有修改过的点直接插入堆中,堆中会有重复元素,但堆中元素总数不会大于 m。
只能处理边权为正数的问题。
图用邻接表存储。
typedef pair<int, int> PII; int n; // 点的数量 int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边 int dist[N]; // 存储所有点到1号点的距离 bool st[N]; // 存储每个点的最短距离是否已确定 // 求1号点到n号点的最短距离,如果不存在,则返回-1 int dijkstra() { memset(dist, 0x3f, sizeof dist); dist[1] = 0; priority_queue<PII, vector<PII>, greater<PII>> heap; heap.push({0, 1}); // first存储距离,second存储节点编号 while (heap.size()) { auto t = heap.top(); heap.pop(); int ver = t.second, distance = t.first; if (st[ver]) continue; st[ver] = true; for (int i = h[ver]; i != -1; i = ne[i]) { int j = e[i]; if (dist[j] > distance + w[i]) { dist[j] = distance + w[i]; heap.push({dist[j], j}); } } } if (dist[n] == 0x3f3f3f3f) return -1; return dist[n]; }
spfa算法
时间复杂度O(km)
基于dp
bellman-ford算法的优化版本,可以处理存在负边权的最短路问题。
最坏情况下的时间复杂度是 O(nm),但实践证明spfa算法的运行效率非常高,期望运行时间是 O(km),其中 k 是常数。
但需要注意的是,在网格图中,spfa算法的效率比较低,如果边权为正,则尽量使用 dijkstra 算法。如果说dijkstra是步步回头找最小,那么SPFA就是一点一圈扩散去。每到一个点,就直接枚举和它相连的所有边和点,如果走这条路可以更近,那么就更新那个点的dist。如果那个点不在即将更新的队列里,那就放进去。也就是十分类似于BFS的一种做法。在这种做法下,每个点可能被放进队列多次,但是都是带着更新前面的点的dist 的可能进去的。
图采用邻接表存储。
队列为手写的循环队列。
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <queue> using namespace std; const int N = 1010, M = 2000010, INF = 1000000000; int n, m; int dist[N], q[N]; // dist表示每个点到起点的距离, q 是队列 int h[N], e[M], v[M], ne[M], idx; // 邻接表 bool st[N]; // 存储每个点是否在队列中 void add(int a, int b, int c) { e[idx] = b, v[idx] = c, ne[idx] = h[a], h[a] = idx++; } void spfa() { int hh = 0, tt = 0; for (int i = 1; i <= n; i++) dist[i] = INF; dist[1] = 0; q[tt++] = 1, st[1] = 1; while (hh != tt) { int t = q[hh++]; st[t] = 0; if (hh == n) hh = 0; for (int i = h[t]; i != -1; i = ne[i]) if (dist[e[i]] > dist[t] + v[i]) { dist[e[i]] = dist[t] + v[i]; if (!st[e[i]]) { st[e[i]] = 1; q[tt++] = e[i]; if (tt == n) tt = 0; } } } } int main() { memset(h, -1, sizeof h); cin >> m >> n; for (int i = 0; i < m; i++) { int a, b, c; cin >> a >> b >> c; add(a, b, c); add(b, a, c); } spfa(); cout << dist[n] << endl; return 0; }
(1)统计每个点入队的次数,如果某个点入队n次说明存在负环(等价于bellman,入队 n 次说明更新 n 次)
(2)统计当前每个点的最短路中所包含的边数,如果某点的最短路所包含的边数大于等于n也说明存在负环(只有 n 个点,正常应为 n-1 条边,大于等于 n 说明有负环多次被加入最短路中)
bool spfa()//返回true有负环 { queue<int> q; for(int i = 1; i <= n; i++) { q.push(i); fl[i] = 1; } while(q.size()) { int t = q.front(); q.pop(); fl[t] = 0; for(int i = h[t]; i != -1; i = ne[i]) { int j = e[i]; if(dist[j] > dist[t] + w[i])//dist数组值为0只有遇到负数才会更新 { dist[j] = dist[t] + w[i]; cnt[j] = cnt[t] + 1; if(cnt[j] >= n) return true; if(!fl[j]) { fl[j] = 1; q.push(j); } } } } return false; }
dijkstra与SPFA这两种算法的核心都是找到另一条路来更新当前的最短路,但是实现方法不大一样。某种程度上说,dijkstra因为即使是堆优化,优先队列的常数也是很大的,而SPFA在稀疏图下步步发散就可以跑得很快,所以有时SPFA可以比Dijkstra快很多,算法的复杂度可以达到O(km)【k为常数】的级别。但是如果是稠密图的话,SPFA也可以退化到O(nm)。所以两种算法也是各有优势,才能一起存活下来。当然,SPFA也是可以用优先队列优化队列的,实现方法最后就和Dijkstra一样了。
floyd算法 O(n3)
标准弗洛伊德算法,三重循环。循环结束之后 d[i][j] 存储的就是点 i 到点 j 的最短距离。
需要注意循环顺序不能变:第一层枚举中间点,第二层和第三层枚举起点和终点。
由于这道题目的数据范围较大,点数最多有1000个,因此floyd算法会超时。
但我们的目的是给出算法模板哦~
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <queue> using namespace std; const int N = 1010, M = 2000010, INF = 1000000000; int n, m; int d[N][N]; // 存储两点之间的最短距离 int main() { cin >> m >> n; for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) d[i][j] = i == j ? 0 : INF; for (int i = 0; i < m; i++) { int a, b, c; cin >> a >> b >> c; d[a][b] = d[b][a] = min(c, d[a][b]); } // floyd 算法核心 for (int k = 1; k <= n; k++) for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) d[i][j] = min(d[i][j], d[i][k] + d[k][j]); cout << d[1][n] << endl; return 0; }
最近公共祖先
向上标记法:
一个点向上走,直到根节点,走的途中标记布尔数组
第二个点向上走,走到第一个被标记的布尔数组,就是最近公共祖先
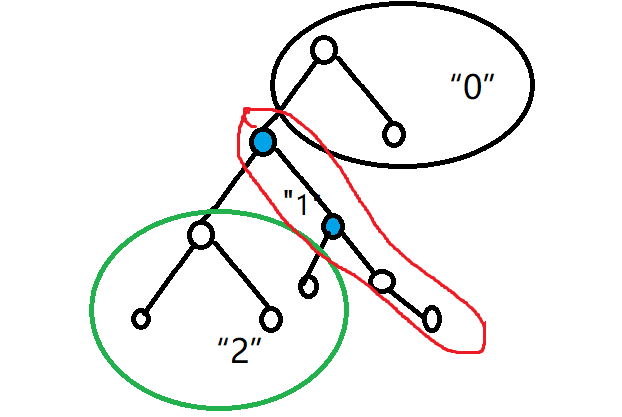
tarjan算法:
O(n+m)
对于向上标记法的优化,离线做法
基于dfs将所有结点分为三类 (1) 已经遍历过,且回溯的——"2" (2) 已经遍历,正在搜索的分支——"1" (3) 还未搜索过的点——"0"
对于每一次:
若现在有结点 x 在 (2) 上,另一个点 y 在 (1) ,则可以将 x 所在子树并入 (2)中如涂蓝色点
给出 n 个点的一棵树,多次询问两点之间的最短距离。
注意:边是无向的。所有节点的编号是 1,2,…,n。
输入格式
第一行为两个整数 n 和 m。n 表示点数,m 表示询问次数;
下来 n−1 行,每行三个整数 x,y,k,表示点 x 和点 y 之间存在一条边长度为 k;
再接下来 m 行,每行两个整数 x,y,表示询问点 x 到点 y 的最短距离。
树中结点编号从 1 到 n。
输出格式
共 m 行,对于每次询问,输出一行询问结果。
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <vector> using namespace std; typedef pair<int, int> PII; const int N = 10010, M = N * 2; int n, m; int h[N], e[M], w[M], ne[M], idx; int dist[N]; int p[N]; int res[M]; int st[N]; vector<PII> query[N]; // first存查询的另外一个点,second存查询编号 void add(int a, int b, int c) { e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ; } void dfs(int u, int fa) { for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (j == fa) continue; dist[j] = dist[u] + w[i]; dfs(j, u); } } int find(int x) { if (p[x] != x) p[x] = find(p[x]); return p[x]; } void tarjan(int u) { st[u] = 1; for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (!st[j]) { tarjan(j); p[j] = u; } } for (auto item : query[u]) { int y = item.first, id = item.second; if (st[y] == 2) { int anc = find(y); res[id] = dist[u] + dist[y] - dist[anc] * 2; } } st[u] = 2; } int main() { scanf("%d%d", &n, &m); memset(h, -1, sizeof h); for (int i = 0; i < n - 1; i ++ ) { int a, b, c; scanf("%d%d%d", &a, &b, &c); add(a, b, c), add(b, a, c); } for (int i = 0; i < m; i ++ ) { int a, b; scanf("%d%d", &a, &b); if (a != b) { query[a].push_back({b, i}); query[b].push_back({a, i}); } } for (int i = 1; i <= n; i ++ ) p[i] = i; dfs(1, -1); tarjan(1); for (int i = 0; i < m; i ++ ) printf("%d\n", res[i]); return 0; }
//倍增法解法 #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int N = 40010, M = N * 2; int n, m; int h[N], ne[M], e[M], w[M], idx; int depth[N]; int fa[N][16];//从 i 结点开始往上走 2^j 个结点的位置 int q[N]; int dist[N]; void add(int a, int b, int c) { ne[idx] = h[a], e[idx] = b ,w[idx] = c, h[a] = idx++; } void bfs(int root) { depth[0] = 0; depth[root] = 1; int tt = 0, hh = 0; q[0] = root; while(hh <= tt) { int t = q[hh++]; for(int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if(depth[j]) continue; depth[j] = depth[t]+1; dist[j] = dist[t] + w[i]; q[++tt] = j; fa[j][0] = t; for (int k = 1; k <= 15; k++ ) { int mid = fa[j][k - 1];//j^k与j^(k-1)的中点的结点 fa[j][k] = fa[mid][k - 1]; } } } } int lca(int a, int b) { if(depth[a] < depth[b]) swap(a, b); for(int k = 15; k >= 0; k--)//底层跳 { int nex = fa[a][k];//a将跳到的结点 if(depth[nex] >= depth[b]) { a = nex; } } if(a == b) return a; for(int k = 15; k >= 0; k--)//一起跳 { if(fa[a][k] != fa[b][k]) { a = fa[a][k]; b = fa[b][k]; } } return fa[a][0]; } int main() { memset(h, -1, sizeof h); scanf("%d%d", &n, &m); for(int i = 0; i < n-1; i++) { int a, b, c; scanf("%d%d%d", &a, &b, &c); add(a, b, c), add(b, a, c); } bfs(1); while(m--) { int a, b; scanf("%d%d", &a, &b); int p = lca(a, b); int ans = dist[a] + dist[b] - dist[p] * 2; printf("%d\n", ans); } return 0; }
倍增法:
预处理:O(nlogn)
查询:O(logn)
fa[i, j]表示从 i 向上走 2^j 所能走到的结点
先用递推预处理:
j = 0, f(i, j) = i 的父结点
j > 0, f(i, j) = f(f(i, j-1), j-1)
depth[i] 表示深度(根节点距离+1)
x 到 y 距离为 d(x) + d(y) - 2d(p)
步骤:
哨兵从 i 开始跳, 若跳过根节点之后,fa[i, j] = 0, depth[0] = 0
1.先将深的跳到和浅的一层(基于二进制拼凑思想)
depth[f(x, k)] >= depth[y] 时
可以跳
2.让两个一起向上跳,一直跳到最近公共先祖的下一层
给定一棵包含 n 个节点的有根无向树,节点编号互不相同,但不一定是 1∼n。
有 m 个询问,每个询问给出了一对节点的编号 x 和 y,询问 x 与 y 的祖孙关系。
输入格式
输入第一行包括一个整数 表示节点个数;
接下来 n 行每行一对整数 a 和 b,表示 a 和 b 之间有一条无向边。如果 b 是 −1,那么 a 就是树的根;
第 n+2 行是一个整数 m 表示询问个数;
接下来 m 行,每行两个不同的正整数 x 和 y,表示一个询问。
输出格式
对于每一个询问,若 x 是 y 的祖先则输出 1,若 y 是 x 的祖先则输出 2,否则输出 0。
思路:
p 为 lca(x, y), d(x) 为 x 到根结点距离
代码:
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int N = 40010, M = N * 2; int n, m; int h[N], ne[M], e[M], w[M], idx; int depth[N]; int fa[N][16];//从 i 结点开始往上走 2^j 个结点的位置 int q[N]; void add(int a, int b) { ne[idx] = h[a], e[idx] = b ,h[a] = idx++; } void bfs(int root) { memset(depth, 0x3f, sizeof depth); depth[0] = 0; depth[root] = 1; int tt = 0, hh = 0; q[0] = root; while(hh <= tt) { int t = q[hh++]; for(int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if(depth[j] > depth[t]+1)//未被遍历过 { depth[j] = depth[t]+1; q[++tt] = j; fa[j][0] = t; for (int k = 1; k <= 15; k++ ) { int mid = fa[j][k - 1];//j^k与j^(k-1)的中点的结点 fa[j][k] = fa[mid][k - 1]; } } } } } int lca(int a, int b) { if(depth[a] < depth[b]) swap(a, b); for(int k = 15; k >= 0; k--)//底层跳 { int nex = fa[a][k];//a将跳到的结点 if(depth[nex] >= depth[b]) { a = nex; } } if(a == b) return a; for(int k = 15; k >= 0; k--)//一起跳 { if(fa[a][k] != fa[b][k]) { a = fa[a][k]; b = fa[b][k]; } } return fa[a][0]; } int main() { memset(h, -1, sizeof h); scanf("%d", &n); int root = 0; for(int i = 0; i < n; i++) { int a, b; scanf("%d%d", &a, &b); if(b == -1) root = a; else add(a, b), add(b, a); } bfs(root); scanf("%d", &m); while(m--) { int a, b; scanf("%d%d", &a, &b); int p = lca(a, b); if (p == a) printf("1\n"); else if (p == b) printf("2\n"); else printf("0\n"); } return 0; }
基于RMQ做法:
首先按照 dfs 遍历根节点,得到一串 dfs遍历结点序 ,x 结点与 y 结点构成的区间中最小的数为 lca
拓扑排序
有向无环图(拓扑图),从前面指向后面。
宽搜做法:
计算所有点的入度 d ,将入度为0的点入队
每次取出队头元素t,
依次遍历t的所有出边 j
d[j]--
若d[j] == 0时,将 j 点放入队列中
深搜做法:
dfs( u )
{
for( u 的所有邻点)
u 加入序列sq中
}
sq为拓扑排序的逆序
二分图
二分环当且仅当图中不含有奇数环(一个环边数为奇数)
染色法
将一个顶点染为1,与它相连且没有染过的点染为-1,若与它相连的点且为1则不是二分图
#include<iostream> #include<algorithm> #include<cstring> using namespace std; const int N = 100010, M = 200010; int n, m; int colur[N]; int h[N], ne[M], e[M], idx; void add(int a, int b){ ne[idx] = h[a]; e[idx] = b; h[a] = idx++; } bool dfs(int v, int c) { colur[v] = c; for(int i = h[v]; i != -1; i = ne[i]) { int j = e[i]; if(colur[j]==c) return false; if(!colur[j] && !dfs(j, -c)) return false; } return true; } bool solve() { for(int i = 1; i <= n; i++) { if(!colur[i]) { if(!dfs(i, 1)) return false; } } return true; } int main() { memset(h, -1, sizeof h); scanf("%d%d", &n, &m); while(m--) { int a, b; scanf("%d%d", &a, &b); add(a, b); add(b, a); } if(solve()) printf("Yes\n"); else printf("No\n"); return 0; }
匈牙利算法
匈牙利算法×(挖墙脚算法)√
我们可以转换找对象问题
遍历每一个男生,如果他有好感的女生没有对象或有对象但是她对象有其他好感女生时,我们可以将当前男生与他有好感的女生撮合成一对
求出最大配对数
#include<iostream> #include<algorithm> #include<cstring> using namespace std; const int N = 510, M = 100010; int n1, n2, m; int colur[N]; int h[N], ne[M], e[M], idx; int match[N]; bool vis[N]; void add(int a, int b){ ne[idx] = h[a]; e[idx] = b; h[a] = idx++; } bool find(int x)//寻找配对 { for(int i = h[x]; i != -1; i = ne[i]) { int j = e[i]; if(!vis[j]) { vis[j] = true; if(match[j] == 0||find(match[j]))//j无配对或j的配对可与其他人配对 { match[j] = x; return true; } } } return false; } int main() { int ans = 0; memset(h, -1, sizeof h); scanf("%d%d%d", &n1, &n2, &m); while(m--) { int a, b; scanf("%d%d", &a, &b); add(a, b); } for(int i = 1; i <= n1; i++) { memset(vis, false, sizeof vis);//赋初值 if(find(i)) ans++; } printf("%d",ans); return 0; }
floyd
基于dp
原理:
d[i, j] = INF
d[i, i] = 0
for( k 1~n )
for( i 1~n )
for( j 1~n)
d[i, j] = min(d[i, j], d[i, k]+d[k, j])
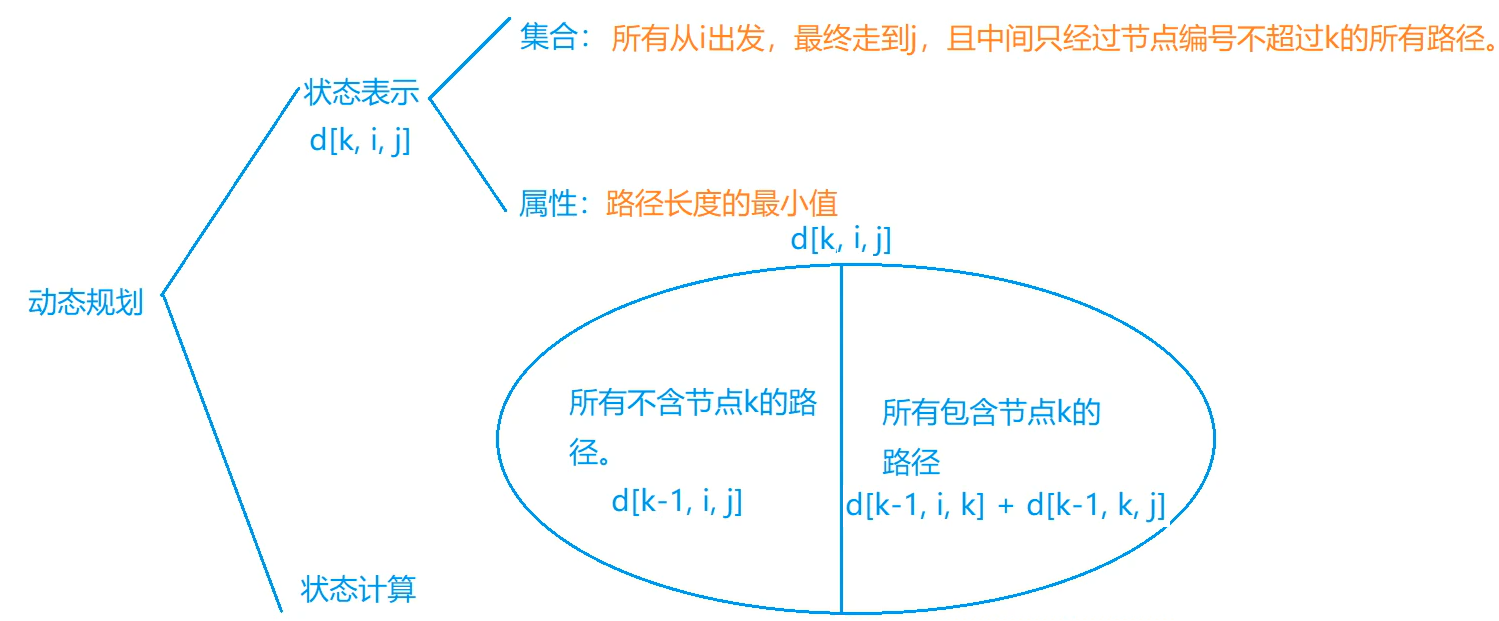
最短路
传递闭包
如果 a 可以到 b ,b 可以到 c 那么我们就认为 a 可以间接的到 c
floyd用邻接阶矩阵存可在 O(n^3) 求出传递闭包
方法:
1.初始化 d[i, j] = g[i, j] (g[i, j] = 1 i, j 相通;g[i, j] = 0, i,j不通)
边权值为1
2.
for(1~K)
for(1~i)
for(1~j)
if( d[i, k] && d[k, j] )// i 可以到 k ,k 可以到 j
d[i, j] = 1;
对于位置如何进行排序:
法1:用一个位置数组来存当前数组的位置,为在它前面的数的个数+1。
法2:将所有点按照 能到达的点数 从小到大排序。然后依次输出编号。
最小环
求小环问题一定不包括重复结点
根据flyod性质
代码模板:
恰好经过k条边的最短路
倍增
联通分量
对于有向图,联通分量:对于分量中任意u,v,必然可以从u走到v,从v走到u
强连通分量:极大连通分量
作用:通过缩点,将任意有向图变成有向无环图(拓扑图)
缩点:将所有联通分量缩为一个点
树枝边,前向边,后向边,横插边
Tarjan:求强连通分量(scc)
对于每个结点 u 有如下定义
dfn[u]表示遍历到 u 的时间戳
low[u]表示从 u 开始走,所能遍历到的最小时间戳是什么
u 是 所在强连通分量的最高点 等价于dfn[u] == low[u],(说明他走不到上面)
时间复杂度 O(n+m)
代码:
void tarjan(int u) { low[u] = dfn[u] = ++timestap; stk[++top] = u, in_stk[u] = true; for(int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if(!dfn[j]){ tarjan(j); low[u] = min(low[u], low[j]); }else if(in_stk[j])//在栈中说明这个点还在某个强连通分量中还没有被遍历 { low[u] = min(low[u], dfn[j]);//求low[u]与当前点的最小值 } if(dfn[u]==low[u])//u自己是它所能遍历的最小点 { int y; ++cnt_scc; do{ y = stk[top--]; in_stk[y] = false; }while(y != u)//y==u时说明我们已经将这个点所在的所有强连通分量处理完 } } }
缩点:
for(1~n)
for( i 的所有邻边)
if(i , j 不在同一个联通块里)
从 i 所在联通分量 到 j 所在联通分量 连一条边
//缩点之后联通分量递减一定是拓扑序
思路:
用tarjan缩点,将所有出度为0的点所在联通块记录
若出度为0的联通块个数大于1输出0
否则输出联通块内点数和
代码:
#include <bits/stdc++.h> using namespace std; const int N = 1e4+10, M = 1e5+10; int h[N], ne[M], e[M], idx; int scc_size[N], scc_cnt;//i号强连通分量大小,强连通分量总数 int low[N] ,dfn[N], timelasp; int stk[N] ,top; bool in_stk[N];int id[N];//i属于的强联通分量编号 int dout[N];//出度 void add(int a, int b) { ne[idx] = h[a],e[idx] = b, h[a] = idx++; } void tarjan(int u) { low[u] = dfn[u] = ++timelasp; stk[++top] = u, in_stk[u] = true; for(int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if(!dfn[j]) { tarjan(j); low[u] = min(low[u], low[j]); }else if(in_stk[j]){ low[u] = min(low[u], dfn[j]); } } if(low[u] == dfn[u]){ int y; ++scc_cnt; do{ y = stk[top--]; in_stk[y] = false; id[y] = scc_cnt; scc_size[scc_cnt]++; }while(y != u); } } int main() { int n, m; scanf("%d%d", &n, &m); memset(h, -1, sizeof h); while(m--) { int a, b; scanf("%d%d", &a, &b); add(a, b); } for(int i = 1; i <= n; i++) if(!dfn[i]) tarjan(i); for(int i = 1; i <= n; i++) { for(int j = h[i]; ~j; j = ne[j]) { int k = e[j]; if(id[i] != id[k]){ dout[id[i]] ++; } } } int sum = 0, root = 0; for(int i = 1; i <= scc_cnt; i++) { if(!dout[i]){ root++; sum += scc_size[i]; if(root > 1) { sum = 0; break; } } } printf("%d", sum); return 0; }
若一个有向图内有 p 个起点 (入度为0点), q 个终点(出度为0点),则加至少加 max(p, q) 条边一定可以将此图变为强联通分量
证明:
1.设|p| <= |Q|
(1)若|p| == 1时
只有一个起点,每一个点都可以到达他的前驱
对于终点,无法到达他的后继,我们加 |Q| 条边使得终点到达起点
此时,对于某一个点,他必然可以到达他的前驱。想要到达其他点,他可以先到终点,从终点到起点,之后可以到达任意点
加 |Q| 条边
(2)若|P| > 1
必然有|Q| >= |p| >= 2
对于任意 Pi 都可以到达某一起点 Qi
我们将某一 Qi 与 Pi+1 连线,将Pi,Qi从P,Q 集合中除掉
|Q'| = |Q| - 1,|P '| = |p| - 1
共重复上述操作|p|-1次
此时|Q''| = |Q| - |P| -1
|p''| = 1
此时形如(1)
得出加 |Q| - (|P| -1)+|P| -1 = |Q|
双联通分量(重联通分量)
桥:无向图中若删掉一个边,这个图变得不联通
割点:在联通图中,若删掉某个点及其相连的边,这个图变得不联通
每个割点都至少属于两个联通分量
两个割点之间的边不一定是桥,桥的两边不一定是割点
(1)边双联通分量e-DCC:极大的,不包含桥的联通块
推出
性质1.边双联通分量中,不管删掉那一条边,这个图还是联通的
性质2.边双联通分量中,任意两点都包含两条不相交(无公共边)的路径
(2)点双联通分量v-DCC:极大的,不包含割点的联通块
求边双联通分量
时间戳
dfn(x)
low(x)
如何找到桥?
若由 x 搜到 y ,y 达到不了 x 的祖先结点,y最高只能到达 y 自己,x,y之间连线为桥
桥<=>dfn(x) < dfn(y)
如何找到边双连通分量?
(1)删掉所有桥,剩下的每一个联通块都是边联通分量
(2)可以用栈
dfn(x) == low(x), 从 x 出发走不到 x 的上面
当前 x 子树的点在栈中的点,是边双连通分量
无向图中至少加 (cnt+1)/2 条可以让此图变为边双联通分量(缩完点之后度数是1的个数)
题目
为了从 F 个草场中的一个走到另一个,奶牛们有时不得不路过一些她们讨厌的可怕的树。
奶牛们已经厌倦了被迫走某一条路,所以她们想建一些新路,使每一对草场之间都会至少有两条相互分离的路径,这样她们就有多一些选择。
每对草场之间已经有至少一条路径。
给出所有 R 条双向路的描述,每条路连接了两个不同的草场,请计算最少的新建道路的数量,路径由若干道路首尾相连而成。
两条路径相互分离,是指两条路径没有一条重合的道路。
但是,两条分离的路径上可以有一些相同的草场。
对于同一对草场之间,可能已经有两条不同的道路,你也可以在它们之间再建一条道路,作为另一条不同的道路。
输入格式
第 1 行输入 F 和 R。
接下来 R 行,每行输入两个整数,表示两个草场,它们之间有一条道路。
输出格式
输出一个整数,表示最少的需要新建的道路数。
代码:
#include <cstring> #include <iostream> #include <algorithm> using namespace std; const int N = 5010, M = 20010; int n, m; int h[N], e[M], ne[M], idx; int dfn[N], low[N], timestamp; int stk[N], top; int id[N], dcc_cnt; bool is_bridge[M]; int d[N]; void add(int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ; } void tarjan(int u, int from) { dfn[u] = low[u] = ++ timestamp; stk[ ++ top] = u; for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (!dfn[j]) { tarjan(j, i); low[u] = min(low[u], low[j]); if (dfn[u] < low[j]) is_bridge[i] = is_bridge[i ^ 1] = true; } else if (i != (from ^ 1)) low[u] = min(low[u], dfn[j]); } if (dfn[u] == low[u]) { ++ dcc_cnt; int y; do { y = stk[top -- ]; id[y] = dcc_cnt; } while (y != u); } } int main() { cin >> n >> m; memset(h, -1, sizeof h); while (m -- ) { int a, b; cin >> a >> b; add(a, b), add(b, a); } tarjan(1, -1); for (int i = 0; i < idx; i ++ ) if (is_bridge[i]) d[id[e[i]]] ++ ; int cnt = 0; for (int i = 1; i <= dcc_cnt; i ++ ) if (d[i] == 1) cnt ++ ; printf("%d\n", (cnt + 1) / 2); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号