OO第一单元总结
程序结构分析：
- 第一次作业：
总体思路：
采用递归下降的方法，对输入表达式进行逐项分析，进行分为式子，项，因子三个层次的提取和运算。其中，以“+”“-”判断式子之间的运算；在提取式子时“*”判断项之间的运算；在提取项时，区分num和x两种因子，以及，“**”判断指数项。对于“(”,“)”则递归进入提取式子的操作，返回值式子作为项。
存储方式：
由于只有常数项和幂指数项，存储容器采用HashMap<Integer,BigInteger>更便于储存和运算以及化简，其中，Integer代表指数的幂次，BigInteger代表系数。
UML类图：
、
类的复杂度分析：
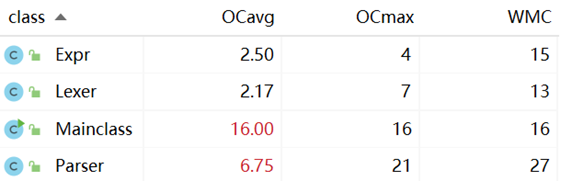
方法的复杂度分析：
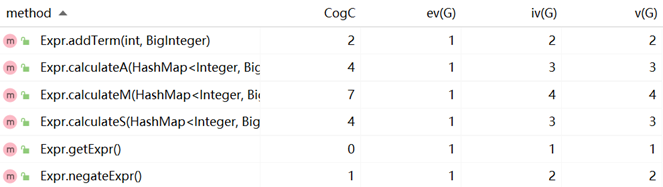
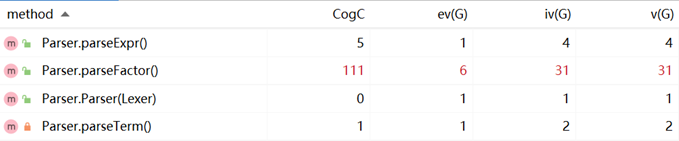
优缺点分析：
优点：
1.可以把表达式当作因子去分析，递归下降更方便接下来的作业的迭代和拓展新功能。
2.没有因子和项这两类，把因子和项也都当作式子，统一定义式子间的加减乘运算，运算的方法复用率高。
缺点：
1.第一次作业表达式只允许一层括号，如果使用正则表达式的话，可以更加简洁并且高效的生成表达式二叉树。
2.没有因子和项这两类，面向对象的特征被削弱，表示起来没那么直观。
- 第二次作业：
总体思路：
仍然采用递归下降的方法，分析式子的总体步骤与第一次作业相同，不同的是在提取因子时除了因子类型常数项和变量又补充了求和函数，自定义函数和三角函数。对于自定义函数，在Parser类中存储了自定义函数，同时把函数项作为参数递归分析以自定义函数为表达式的式子，返回值为以式子为元素的因子。对于求和函数，根据相应格式，提取上下界，之后把i作为参数，进入for循环，循环相加对应参数i下的式子的结果。
存储方式：
由于三角函数的存在，此次作业的项的存储不能只用一个HashMap处理，我采用的存储方式如图1， 每个式子是一个以x的指数为key，以一个ArrayList为value的HashMap，ArrayList的元素是三角函数乘积项，代表着所有幂指数为Key的乘积项的加和，其中，每个乘积项由系数和四个HashMap组成，系数即代表此项的系数，四个HashMap则分别为以乘积项中函数内部的元素为key，以外部指数为value表示一个项中所有乘积项的sin和cos函数因子。
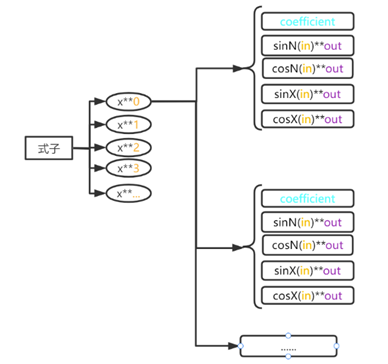【存储结构示意图】
UML类图：
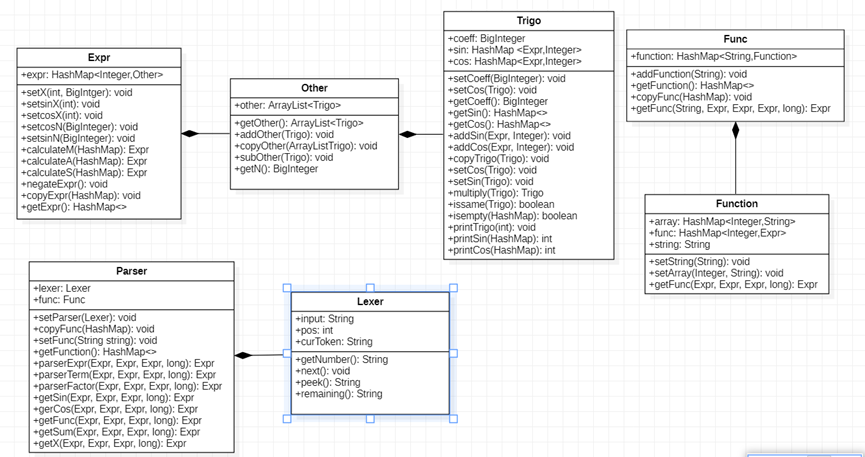
类的复杂度：
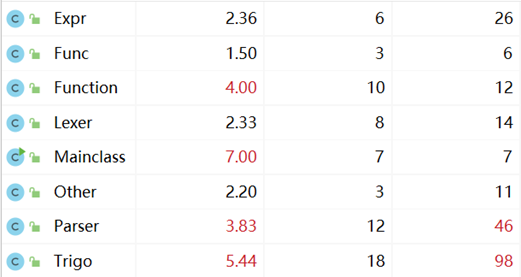
方法的复杂度：
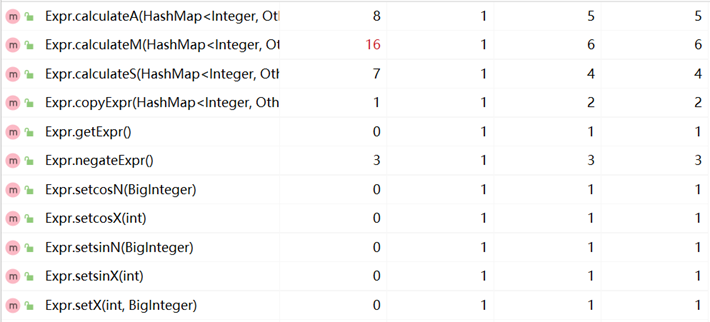
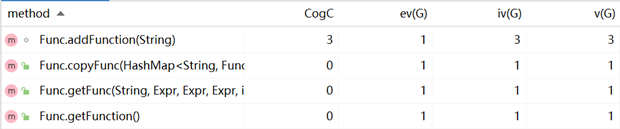
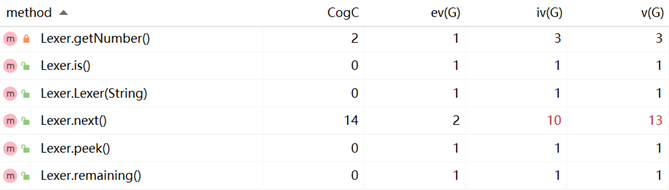
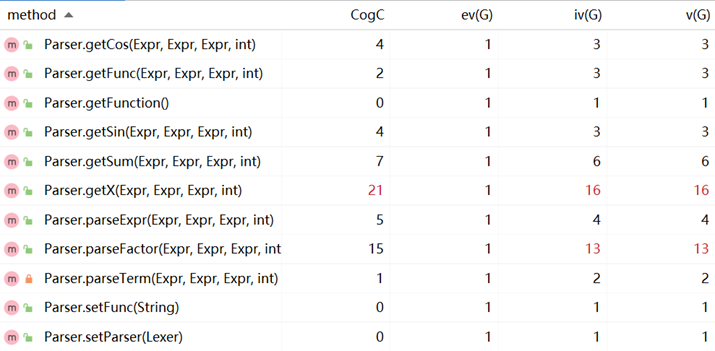
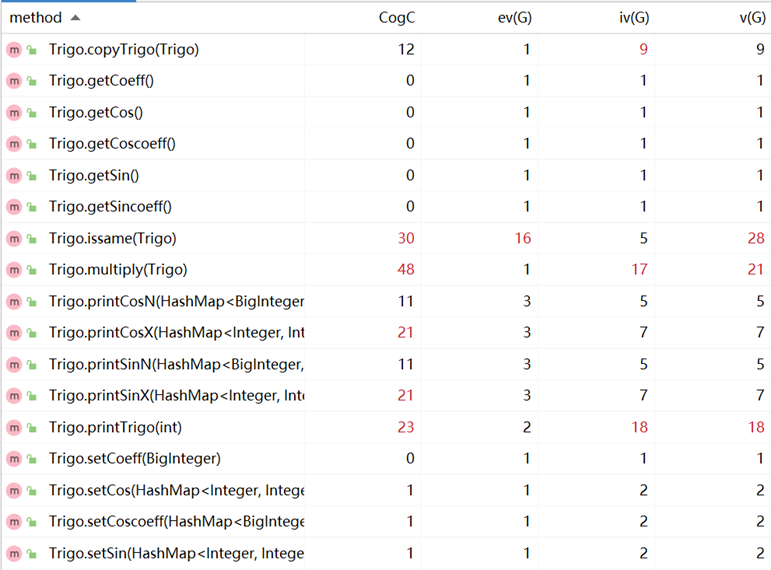
优缺点分析：
优点：
1.较大程度的保留了第一次作业的结构，
2.在处理此次作业拓展的自定义函数和求和函数时，采用了把自定义函数的参数和求和函数的i的赋值作为参数递归进入下一层函数去分析，可拓展性好，便于迭代。
3.所有因子和项都作为式子去处理运算，并且不同函数之间耦合度低，再添加新的运算或者函数类型时，只需要增加新的方法就好，便于拓展。
4.以x的指数为式子的第一层HashMap的key值的存储结构，以乘积项作为因子，方便式子的合并同类项。
缺点：
1.传递参数再分析需要的内存大且效率慢，不如直接字符串替换高效。
2.由于把所有因子也当作式子去运算，面向对象的概念相对较弱，当需要拓展三角函数、qiu和函数和自定义函数时，不是增添新的因子类，或运算类，而是增加了运算和提取因子的方法，不符合我们这门课的核心理念。
3.采用较多HashMap存储结构，效率较低。
- 第三次作业
总体思路：
本次作业要求相较于第二次作业变化不太大，允许了函数嵌套。在提取和运算方面，此次作业与第二次作业逻辑上几乎一致。不过存储结构变化较大。由于是以式子为三角函数的HashMap的key值，需要写一个比较判断是不是相同项的函数。
存储结构：
如图所示，对于每个x的指数对应的ArrayList的元素均是一个系数和两个HashMap的结构，其中，HashMap以一个乘积项中三角函数因子的内部式子为key值，以该因子的指数为value。
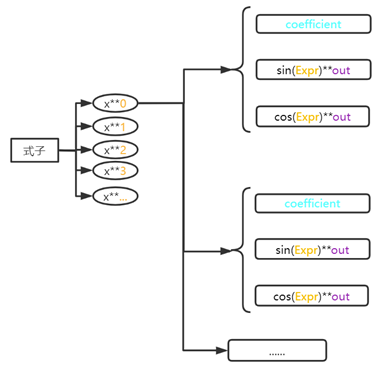
【第三次作业存储结构示意图】
UML类图：
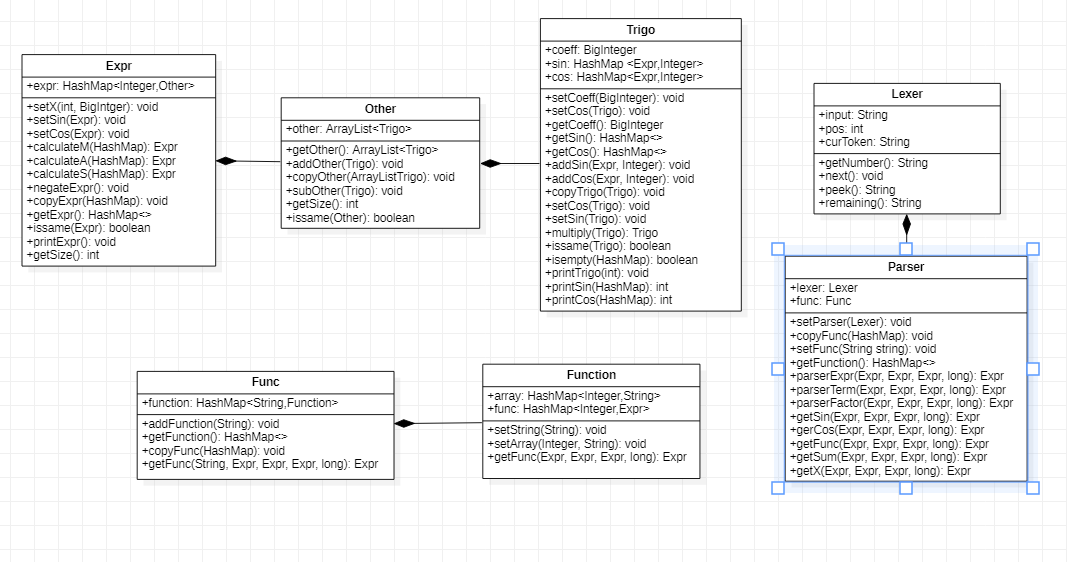
类复杂度分析：
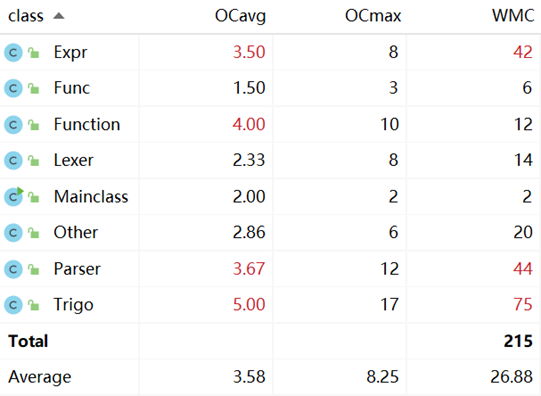
方法复杂度分析：
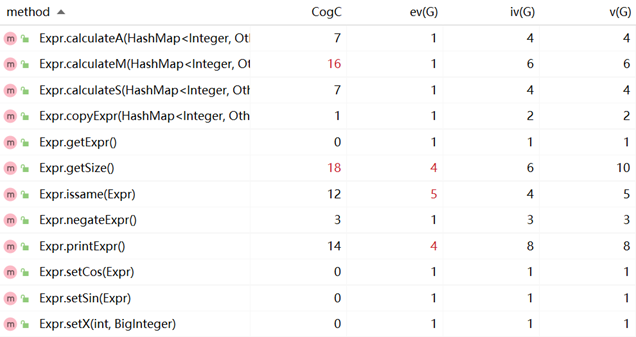
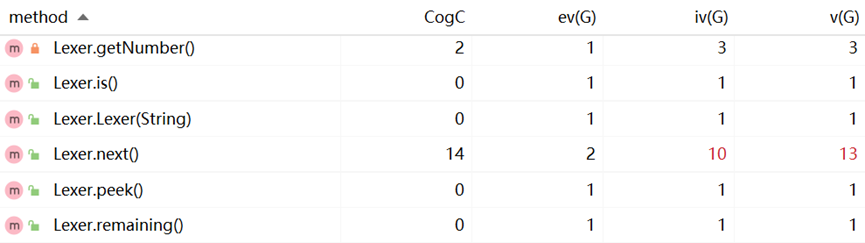
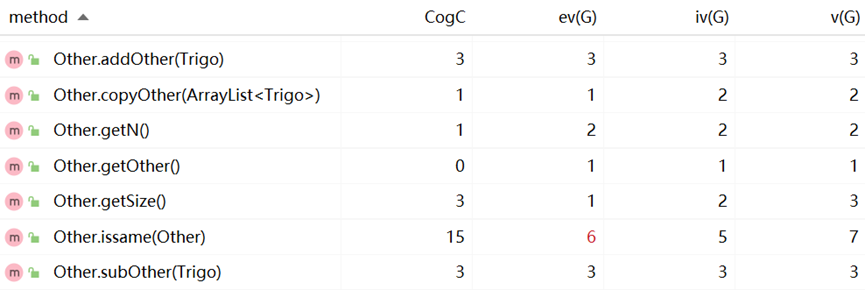
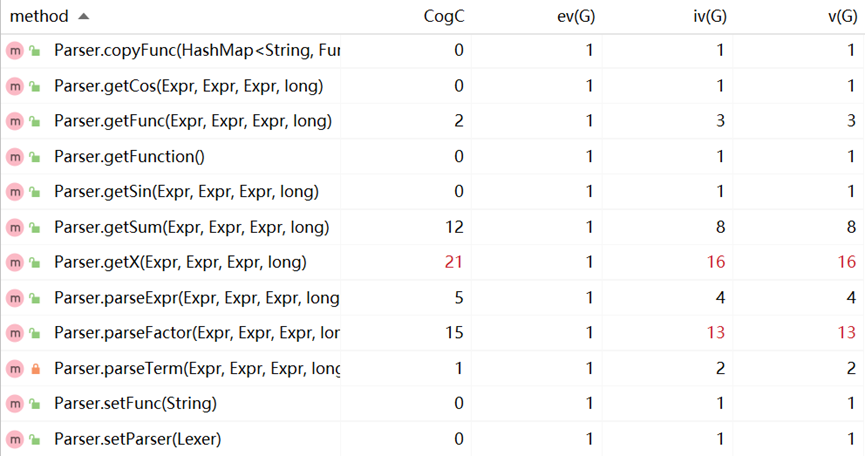
优缺点分析：
优点：此次作业采取的存储结构方便合并同类项的化简及运算。
缺点：
1.一个乘积项中三角函数因子是用以Expr为key值得HashMap来表示的，在运算合并时，需要用编写的比较函数对一个HashMap的全部key遍历比较是否相同，效率低
2.递归时的参数传递需要深克隆及new一个一模一样的新的对象作为参数传递进下一层函数中，内存消耗大。
3.由于嵌套层数较多，且每一层是以式子为对象，三角函数的“属性”不容易比较，对于三角函数的化简则较为困难。
BUG分析：
① 在类Func中的方法addFunction中，添加函数时忽略了对空白符的判断。在处理表达式中的“\s”和“\t”时都是采用String.replace(“”,“”)在读入后就预处理的方式，但是却忘记预处理读入的自定义函数中的“\s”和“\t”，导致强测出现RE错误。
② 类Parser，的方法getSum中，忘记处理上下界中出现的+符号，导致RE的错误；
③ 类Parser的方法getSum中，忘记考虑第一个参数可以大于第二个参数的情况，出现逻辑错误
④ 类Parser的方法getSum中，用int存储上下界，但是题目中可能出现的情况最大的值是long型来表示。
上述中的三个bug的出现其实与代码行和圈复杂度都无关，主要是在迭代过程中忽略了上次作业的既有要求！空白符、“+”、int都是在第一次作业中需要重点处理的因素，但是在第二次和第三次迭代中就忽略掉了，导致在添加新的方法和类的时候出现了bug。对于第三个bug，则也是忽略题目具体说明所导致的。
架构设计体验：
三次作业的分析思路均是受training中所提供的代码思路启发，采用递归下降的方法，对每一层的式子进行项的分析，对每一层的项进行对因子的分析，其中，因子又分为原子因子和递归进入下一层式子的分析所得到的式子因子，依次循环递归分析整个表达式，是这三次作业统一采用的分析结构。每一次作业我们首先要根据作业的要求及实现途径确定我们所选择的对象，我在这三次作业中，把所有的运算对象均抽象为表达式这一类，即因子、项、式子均抽象成表达式这一类，其出发点是所有的他们都可以具有相同的属性，同时可以利用一套相同的规则进行两个元素之间的运算，在确定好对象之后，就完成了最初步的结构设计。具体的，由于所实现的结构不同，每次作业所选择的对象均为表达式，我们需要为对象确定具体的合理的可实现的属性以及方法，就如上文中所说的存储结构，针对每次作业的对象的具体实现的要求不同所确定的不同的存储结构。表达式中所有的函数或者运算均可以通过传递参数和加减乘除实现，所以，每次主要是根据对象的属性确定标准的加减乘除运算。由第一次作业向第二次作业迭代时，增加了三角函数和自定义函数，这两个函数的增加，对象以及运算方法在根本上仍旧是不变的，但是我们需要添加函数类来满足自定义函数；由第二次作业向第三次作业迭代时，由于多层函数的嵌套，我们需要重新写比较函数和克隆函数。不难发现，只要在第一次作业中确定比较合适的架构，每次作业的迭代均是增加新的功能来实现。我的第一次作业采用的“递归”和以“表达式”为对象为每次作业的可拓展性打下了一定的基础。当然，在添加方法时，不仅是为了满足新的要求与目的，还要记得之前已经提出的既有的要求。
总之，每次作业的架构设计，都是先根据作业要求抽象总结出统一的对象，再根据作业要求的实现步骤，确定对象的属性以及合适的存储结构，最后由属性的变化方式确定修改相应的方法。
发现别人BUG的思路：
hack时，我一般采用的是试比较特殊的数据。对于和0，1和爆int的值有关的很多数据，大家普遍情况下或是为了化简或是输出的要求，通常情况下，这些特殊数据的输出是需要特判的，比如指数为0或1的项或者因子，最终结果为0或1，或者sin的因子是2次幂的式子。所以，每次找bug时都会格外注意这些特殊的数据。此外，还是试一些函数组合或者函数之间的嵌套，还会注意函数作为开头元素、中间元素和末尾元素以及函数与函数加减乘除关系，而且，尤其需要注意0作为因子或者指数的情况。
心得体会：
第一单元的作业使我迅速提高了Java的使用能力，练习了继承和接口的用法，同时通过作业，体会面向对象的思想，体会对象的“属性”以及“改变属性”的概念。具体的还有比较细节的深入的理解和使用递归和深克隆。
但是，每次迭代需要修改大量代码，不符合工程化“添加代码”的要求，代码的灵活性以及可拓展性不高，最根本原因是在最一开始写代码的时候没有设计好一个更容易拓展的架构，出发点只是实现此次作业的目的，没有思考自己代码的架构究竟是否合适。
此外，值得反思的是以后除了关注自己代码的整体架构和逻辑之外，更要注意题目细节，比如本单元中“\s” “\t”的处理和数据的范围，题干都有具体的要求，但是由于忽略掉这些细节因素，即使逻辑再对，也还是会有大量bug......QAQ
