loj#10013 曲线(三分)

题目

#10013. 「一本通 1.2 例 3」曲线

解析

首先这个题保证了所有的二次函数都是下凸的， \(F(x)=max\{s_i(x)\}i=1...n\)在每一个x上对应的最大的y，我们最后得到的还是一个凸函数

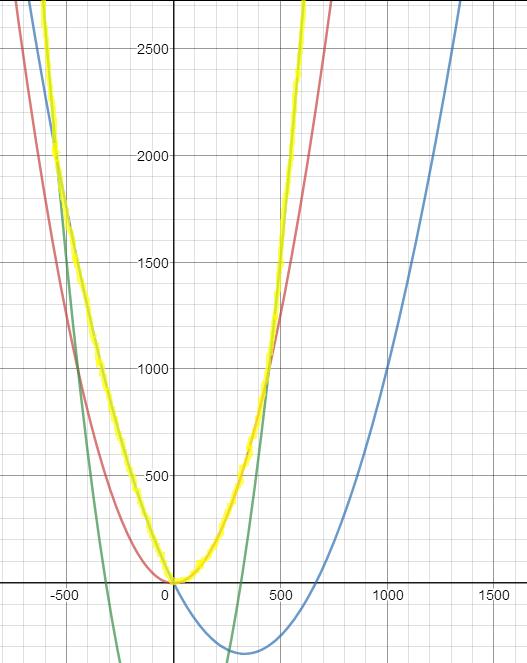
这个题比较特殊的一点是函数可能退化为一次，但退化为一次后的函数还是凸函数

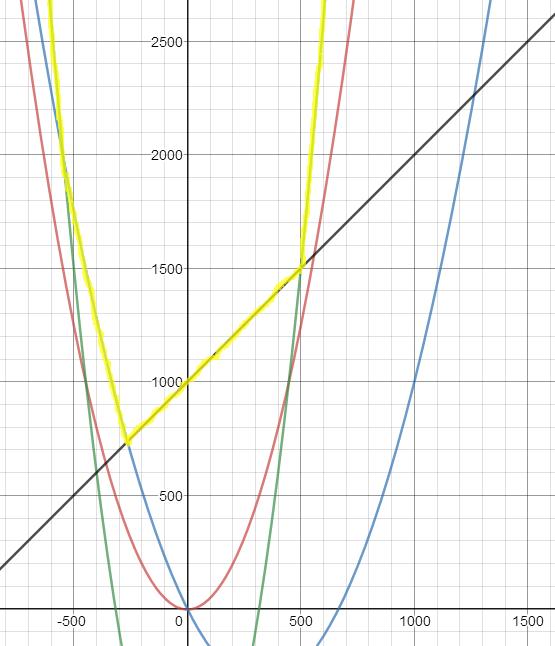
代码

然后就可以愉快的三分了

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;
const double EPS = 0.000000001;

int t, n;

double a[N], b[N], c[N];
double l, r, lm, rm;
double data[N];

double f(double x) {
	double ret = -0x3f3f3f3f;
	for (int i = 1; i <= n; ++i) ret = max(ret, a[i] * x * x + b[i] * x + c[i]);
	return ret;
}

int main() {
	cin >> t;
	while (t--) {
		cin >> n;
		for (int i = 1; i <= n; ++i)
			cin >> a[i] >> b[i] >> c[i];
		l = 0.0, r = 1000.0;
		while (r - l > EPS) {
			lm = l + (r - l) / 3, rm = r - (r - l) / 3;
			if (f(lm) > f(rm)) l = lm;
			else r = rm;
		}
		printf("%.4lf\n", f(l));
	}
}