CF1004D Sonya and Matrix

思维，构造

题解

已知一个无限大的矩阵，其中每个格子的值表示其距离矩阵中心的曼哈顿距离。

如图是矩阵的一部分：

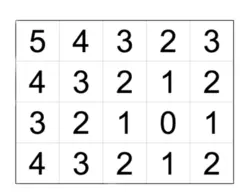
现在另一个矩阵，已知矩阵中全部的 \(t\) 个数，试在无限大的矩阵中截取出 \(n\times m =t\) 大小的矩阵，使得其出现的数与给定的相同。

输出矩阵大小以及 \(0\) 出现的位置。

\(1\leq t\leq 10^6\), \(0\leq a_i< t\)

题解

规定矩阵大小为 \(n\times m\)，\(0\) 的坐标为 \((x,y)\)。

很明显可以枚举 \(t\) 的因数求出 \(n,m\)。

考虑如何确定 \(x,y\)。显然，对于第一个没有出现 \(4x\) 次的 \(x\)，一定是因为被框起来了，可以据此判断出 \(x\)。（为了方便，规定 \((x,y)\) 在矩阵的左上部分）

\(y\) 也很好求，矩阵右下角的数是固定的，即所有数字的最大值 \(mx\)。那么 \(y=n+m-mx-x\)。

对于每一组 \(n,m,x,y\) 暴力检验即可。

代码

#include<bits/stdc++.h>
// #define int long long
using namespace std;
const int Maxn=1e6+10;
int f[Maxn],g[Maxn];
int n,m,x,y,mx;
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int T; cin>>T;
    for(int i=1;i<=T;i++) {int x; cin>>x; f[x]++; mx=max(mx,x);}
    if(T==1)
    {
        if(f[0]==1) cout<<"1 1"<<endl<<"1 1"<<endl;
        else cout<<-1<<endl;
        return 0;
    }
    else if(f[0]>1) return (cout<<-1<<endl,0);
    for(int i=1;i<=mx;i++) if(f[i]<4*i) {x=i;break;}
    for(int k=1;k<=T;k++) if(T%k==0)
    {
        n=k,m=T/k;
        y=n+m-mx-x;
        memset(g,0,sizeof(g));
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                g[abs(x-i)+abs(y-j)]++;
        bool flag=1;
        for(int i=1;i<=mx && flag;i++) if(f[i]!=g[i]) flag=0;
        if(flag) return (cout<<n<<" "<<m<<endl<<x<<" "<<y<<endl,0);
    }
    cout<<-1<<endl;
    return 0;
}