matlab协方差矩阵计算函数
一、协方差矩阵的定义及其计算公式
协方差矩阵在机器学习中经常用到,查看wiki:http://zh.wikipedia.org/wiki/%E5%8D%8F%E6%96%B9%E5%B7%AE%E7%9F%A9%E9%98%B5 可知协方差矩阵的具体计算公式如下:
在统计学与概率论中,协方差矩阵是一个矩阵,其每个元素是各个向量元素之间的协方差。这是从标量随机变量到高维度随机向量的自然推广。
假设 是以
是以 个标量随机变量组成的列向量,
个标量随机变量组成的列向量,
并且 是其第i个元素的期望值,即,
是其第i个元素的期望值,即, 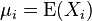 。协方差矩阵被定义的第i,j项是如下:
。协方差矩阵被定义的第i,j项是如下:
即:
矩阵中的第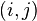 个元素是
个元素是 与
与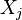 的协方差。这个概念是对于标量随机变量方差的一般化推广。
的协方差。这个概念是对于标量随机变量方差的一般化推广。
二、理解的关键
1、理解的关键是两个随机变量x1,x2的协方差如何计算,有cov(x1,x2) = E{[(x1-E(x1)][x2-E(x2)]},对于离散的随机变量x1,x2,协方差矩阵描述的x1,x2相互联系的偏差,所以两个随机变量是一一对应的,即假设有m个样本值,则分别为(x11,x21),(x12,x22),(x13,x23),...(x1m,x2m),这便可以写成一个2*m的矩阵的形式。则x1,x2协方差表示的是两个随机变量对应的样本值分别都减去各自均值后的乘积的均值(因为无偏性估计的缘故,除以的不是m而是m-1);
2、所以对于一个n*m的样本矩阵,得出的协方差矩阵C是n*n的矩阵,协方差矩阵每个元素Cij表示的随机变量xi,xj的协方差。所以协方差矩阵是一个对称矩阵,且对角线上元素为每个随机变量的方差(如果是信号的话可以看成是能量);如果各个变量相关性很小的话,互相的协方差接近0,即协方差矩阵基本上为对角阵;
3、可以证明,协方差矩阵是非负定矩阵,这可以有非负定矩阵的定义得到;(参考北京大学出版社《多元统计分析》)
4、同样地,为了表示各个随机变量相关性到底有多大,可以引入相关性矩阵。
三、matlab计算公式:
matlab中有一个计算协方差矩阵的函数cov,从其help中可知,该函数的输入为一个m*n的矩阵X,其定义和wiki上的定义相反,每一行表示一个随机向量,即有n个随机变量。如果将一个随机向量看成一个模式的特征向量的话,那么该矩阵表示该模式的一个特征向量用n个特征表示,共有m个特征向量,即有m个样本。
根据matlab中的help文档的cov函数介绍写一个类似的函数:
1 function cov = covariance(X) 2 % 由随机变量样本矩阵计算协方差矩阵 3 %---- 输入: 4 % X: M*N的样本矩阵,其中一行表示一个随机向量样本 5 % 共有M个随机样本 6 %---- 输出: 7 % cov: N*N的协方差矩阵,表示各个随机变量的协方差 8 %---- 计算方法 9 % 随机变量均值用样本均值统计量估计:X_mean = 1/N*ΣXi; 10 % 随机变量方差用样本方差统计量估计:S = 1/(N-1)*Σ(Xi-X_mean)^2 11 % 随机变量协方差可以用如下统计量估计:C = 1/(N-1)*Σ(Xi-X_mean)(Yi-Y_mean) 12 13 % 各个样本减去其平均值 14 % X = bsxfun(@minus,X,mean(X)); 15 %或者: 16 %X = X-repmat(mean(X),size(X,1),1); 17 cov = 1/(size(X,1)-1)*X'*X;



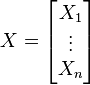

![\Sigma=\mathrm{E}
\left[
\left(
\textbf{X} - \mathrm{E}[\textbf{X}]
\right)
\left(
\textbf{X} - \mathrm{E}[\textbf{X}]
\right)^\top
\right]](http://upload.wikimedia.org/math/1/8/1/1811f942680a72974597be42c28d31d2.png)
![=
\begin{bmatrix}
\mathrm{E}[(X_1 - \mu_1)(X_1 - \mu_1)] & \mathrm{E}[(X_1 - \mu_1)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_1 - \mu_1)(X_n - \mu_n)] \\ \\
\mathrm{E}[(X_2 - \mu_2)(X_1 - \mu_1)] & \mathrm{E}[(X_2 - \mu_2)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_2 - \mu_2)(X_n - \mu_n)] \\ \\
\vdots & \vdots & \ddots & \vdots \\ \\
\mathrm{E}[(X_n - \mu_n)(X_1 - \mu_1)] & \mathrm{E}[(X_n - \mu_n)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_n - \mu_n)(X_n - \mu_n)]
\end{bmatrix}](http://upload.wikimedia.org/math/a/1/2/a12a573ecd1d853abd8c01fab9fccfbe.png)

 浙公网安备 33010602011771号
浙公网安备 33010602011771号