Gym100851K King's Inspection（哈密尔顿回路）

Description

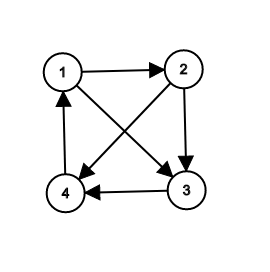
给你一张 $n$ 个点 $m$ 条边的有向图，求这张图 $1\to 1$ 的汉密尔顿回路。

$1\le n\le 10^5,1\le m\le n+20$

Solution

哈密尔顿回路是一个 NP 完全问题，复杂度是指数级的，但是 $1\le m\le n+20$，这代表图中有许多的出度为 $1$ 的点，出度为 $1$ 的点是不用跑的，所以将出度为 $1$ 的点在图中标记为已经访问。那么坏的情况是每个点的出度为 $2$，图中有许多三角形拼接起来，那么最多有 $20$ 个这样的点，$2^{20}$ 也不慌。

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
inline int read() {
	int x = 0, f = 0; char ch = 0;
	while (!isdigit(ch)) f |= ch == '-', ch = getchar();
	while (isdigit(ch)) x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
	return f ? -x : x;
}
struct edge{
    int to, nxt;
}e[N];
int head[N], tot;
void addedge(int x, int y){
    e[++tot].to = y, e[tot].nxt = head[x], head[x] = tot;
}
int n, m, deg[N], vis[N], mark[N], nxt[N];
vector <int> cur;
bool check() {
	memset(mark, 0, sizeof(mark));
	for (int i = 1, x = 1; i <= n; i++, x = nxt[x]) {
		if (mark[x]) return 0;
		mark[x] = 1;
	}
	return 1;
}
void dfs(int t){
    if (t == cur.size()){
    	if (check()) {
    		for (int i = 1, x = 1; i <= n; i++, x = nxt[x]) printf("%d ", x);
   			puts("1"); exit(0);
    	}
   		return ;
    }
    int x = cur[t];
    for (int i = head[x]; i; i = e[i].nxt) {
    	int y = e[i].to;
    	if (!vis[y]) {
    		nxt[x] = y;
    		vis[y] = 1; 
			dfs(t + 1); 
			vis[y] = 0;
    	}
    }
}
int main() {
	//freopen("king.in", "r", stdin);
	//freopen("king.out", "w", stdout);
	n = read(), m = read();
	for (int i = 1; i <= m; i++) {
		int x = read(), y = read();
		addedge(x, y); deg[x]++;
	}
	for (int i = 1; i <= n; i++) {
		if (deg[i] >= 2) cur.push_back(i);
		else if (deg[i] == 0) {
			puts("There is no route, Karl!"); 
			return 0;
		} else {
			if (vis[e[head[i]].to]) { 
				puts("There is no route, Karl!");
				return 0;
			}
			vis[e[head[i]].to] = 1;
		}
		nxt[i] = e[head[i]].to;
	}
	dfs(0);
	puts("There is no route, Karl!");
	return 0;
}