20SD夏令营高级班 简单的网络流和费用流

模板

网络最大流

P2756 飞行员配对方案问题

求二分图最大匹配，并输出方案。

建模比较简单，对于可以匹配的连一条有向边，容量设为 $1$。再让 $S$ 和 $T$ 分别与两个点集相连，容量设为 $1$ 或 $\infty$ 即可。

while (~scanf("%d%d", &x, &y) && ~x && ~y){
	addedge(x, y, 1); addedge(y, x, 0);
}
for (int i = 1; i <= n; i++) {
	addedge(s, i, 1); addedge(i, s, 0);
}
for (int i = n + 1; i <= m; i++) {
	addedge(i, t, 1); addedge(t, i, 0);
}

考虑如何打印方案。如果一条边选择了，那么它的反向边容量一定非 $0$，跑完网络流判断一下即可。

for (int x = 1; x <= n; x++) {
    for(int i = head[x]; i; i = e[i].nxt) {
        int y = e[i].to, z = e[i].z;
        if(y != s && !z && e[i ^ 1].z == 1) 
			printf("%d %d\n", x, y);
    }
}

POJ3281 Dining

有 $f$ 种食物和 $d$ 种饮料，每种食物或饮料只能供一头牛享用，且每头牛只能享用一种食物和饮料。 现在有 $n$ 头牛，每头牛都有自己喜欢的食物种类列表和饮料种类列表，问最多能使多少头牛同时享用到自己喜欢的食物和饮料。

$1\le n,f,d\le 100$

把一头牛看成一条边，连接饮料和食物，跑二分图最大匹配即可。

SDOI 2015 星际战争

有 $n$ 个武器和 $m$ 个敌人，敌人血量为 $a_1\sim a_n$。每个武器可以攻击若干指定的敌人，第 $i$ 个武器可以每秒打击一个敌人的 $b_i$ 点血量，武器的攻击是连续的，你可以把一秒的打击时间分给任意个敌人。所有武器可以同时攻击，求最少需要多长时间才能干掉全部敌人。精度误差允许范围为 $10^{-3}$。

$1\le n,m\le 50$。

要求最大时间最小，先二分 $t$，那么看看 $t$ 时间内能不能打击完全部敌人。不考虑精度误差，可以这样建模

因为精度误差允许范围为 $10^{-3}$，所以先让容量 $\times 10^{-3}$，最后再除掉即可。

HNOI 2007 紧急疏散

Description

又是而分体的套路。因为要求最后一个撤离的人撤离的尽可能早，所以二分 $t$。那么对于每个门，把它拆成 $t$ 个点，那么在时间 $i\in [1,t]$ 只允许通过一个人。然后 bfs 预处理每个人到每扇门所需要的时间，对时间的后缀连边。

但因为边数太多，会炸掉。我们用一个对后缀建模优化的小 trick 就行。

POJ 1336 The K-League

有 $n$ 支队伍进行比赛，每支队伍需要打的比赛数目相同。每场比赛恰好一支队伍胜，另一支败。给出每支队伍目前胜的场数和败的场数，以及每两个队伍还剩下的比赛场数，确定所有可能得冠军的球队。夺冠即为获胜场数最多，可以并列。

$1\le n\le 25$。

先枚举谁胜，让它能赢的全赢，再它他排除了。现在要判断其它队伍能不能通过合理的分配使得没有一个队伍的分比它高。那么也是用到了两两比赛的建模技巧，把一场比赛看作一个点，分别连向两个人获胜的状态即可。

---

最小费用最大流

ZJOI 2010 网络扩容

给定一张有向图，每条边都有一个容量 $c$ 和一个扩容费用 $w$。这里扩容费用是指将容量扩大 $1$ 所需的费用。求

• 在不扩容的情况下，$1$ 到 $n$ 的最大流;
• 将 $1$ 到 $n$ 的最大流增加 $k$ 所需的最小扩容费用。

第一个就是最大流模板了。第二个我们在残余网络上建模。为了正好增加 $k$，从源点连一条容量为 $k$ 的边到虚拟点即可。

HAOI 2010 订货

Description

考虑对每个月的仓库建一个点，月与月间的限制为 $m$。再用一个点当作商品，连向每个月的仓库，流量为 $\infty$，花费为单价 $d_i$，再把每个仓库连向汇点。其实这是用的分层图思想，在建模中比较常见。

JSOI 2009 球队收益

在一个篮球联赛里, 有 $n$ 支球队。第 $i$ 支球队的赛季总支出是 $c_i\times x^2+d_i\times y^2(D_i\le C_i)$。其中 $x,y$ 分别表示这只球队本赛季的胜负场次。现在赛季进行到了一半，每只球队分别取得了 $a_i$ 场胜利和 $b_i$ 场失利。而接下来还有 $m$ 场比赛要进行。问联盟球队的最小总支出是多少。

$2\le n\le 5000,0\le m\le 1000,0\le d_i\le c_i\le 10,0\le a_i,b_i\le 50$

这个式子同时考虑了赢场和输场，比较难受，直接让所有队伍都输。那么对于每场比赛，两个队伍中有一个要赢，这个建模的套路上文提到过了，不再赘述。那么考虑每次增广，可能让好几个队伍获胜了，那么有个平方比较难受，直接写一下式子，看看能不能把平方消掉

$$\begin{array}{c}{c}_i(x+1{)}^2+d_i(y-1{)}^2-c_i{x}^2-d_i{y}^2\\ =c_i+d_i+2c_{i}x-2d_{i}y\end{array}$$

可以发现，这个式子是单调递增的，要让递增的最小，是最小费用最大流。那么接下来就神仙起来了，我们把边拆成了 $S$ 条，$S$ 为一个人的比赛场数。挂一下建模的伪代码

枚举胜者
	j 从 1 到 S
		add(胜者, 汇点, 费用为 c[j] + d[j] + 2 * c[j] * x - 2 * d[j] * y, 容量为 1);
		x++, y--;

---

最小割

Trick & Tip

• 最小割的建模的意义大多为，将一部分点分到 $S$ 集合，将令一部分点分到 $T$ 集合。

• 最小割建模中有许多无向边，需要警惕。

• 众所周知，选的边代价应尽可能小。那么把一个点与 $S$ 相连的代价为 $a$，与 $T$ 相连的代价为 $b$。那么建模时要把代价倒过来，女少口β可

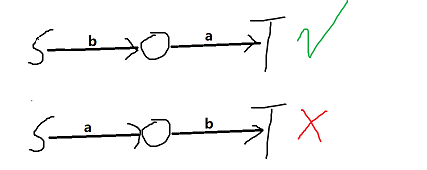
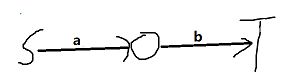
• 那么选的边价值尽可能大怎么办？这个直观一点，先把所有边都选了，然后正常建模跑最小割。其实就是取了个补集。
  

ZJOI2009 狼和羊的故事

给定一个地图，有的格子有狼，有的格子有羊，有的是公共领域。开始地图边缘有一圈篱笆，你要围最少的篱笆，满足狼不能吃到羊。

$1\le n,m\le 100$

明显的最小割了，把地图相邻两个位置用无向边连起来，容量都为 $1$。用 $S$ 连向所有的羊，用 $T$ 连向所有的狼。跑最小割即可。

不需要图吧.jpg

SHOI2007 善意的投票

有 $n$ 个小朋友进行投票决定睡觉还是不睡觉。每个人都有自己的主见，但他们还想考虑朋友的想法。定义冲突值为好朋友间的冲突和与自己的主见冲突的人数，求最小的冲突值。

$2\le n\le 300$

把同意的人分给 $S$，不同意的人分给 $T$，再给朋友连无向边，容量都为 $1$。

不需要图吧.png

BZOJ 1976 能量魔方

Description

一道神仙题。

先考虑在二维平面上的问题，扩展到三维是相似的。

先考虑相邻格子水晶相同才会产生能量的情况。

要让价值最大，那么求个补集，再用最小割求最小的损失。那么让 $S$ 和 $T$ 代表两个不同的水晶类型。在相邻的格子之间，连容量为 $1$ 的无向边。

• 如果一个格子已经钦定为正水晶，那么连一条 $S$ 到它的，容量为 $\infty$ 的边。
• 如果一个格子已经钦定为负水晶，那么连一条它到 $T$ 的，容量为 $\infty$ 的边。

这样我们巧妙的强制一些点选什么水晶。

那么再考虑相邻格子水晶不同才会产生能量的情况，这就用到了网格中常用的黑白染色。

我们让相邻的格子连向 $S$ 和 $T$ 所表示的意义不同。具体的，如果两个点相邻，那么它们的横纵坐标之和奇偶性不同。所以将偶数的 $S$ 通往正水晶，$T$ 通往负水晶，奇数的反过来即可。

大概可能也许不需要图吧.jepg

---