2025“钉耙编程”中国大学生算法设计暑期联赛(3)02/07/08/12
个人做题顺序/大致难度排序
1. 1002 小抹爱锻炼
知识点:注意力
只要根据题意计算出训练次数的下限和上限,判断 \(M\) 是否在上下限区间中即可
下限:因为训练次数要保证单调不降,所以下限 \(b[i]\) 必须是 \(b\) 数组的前缀最大值
上限:因为训练次数要保证单调不降,所以上限 \(c[i]\) 必须是 \(c\) 数组的前缀最小值
对 \(c\) 和 \(b\) 数组分别求和即为训练次数的最大最小值。
#include<bits/stdc++.h>
#define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e18;
const int mod = 998244353;
void solve(){
int n,m;
cin>>n>>m;
vector<int> c(n+1),b(n+1);
int mn=0;
for(int i=1;i<=n;i++){
cin>>b[i];
b[i]=max(b[i],b[i-1]);
mn+=b[i];
}
for(int i=1;i<=n;i++){
cin>>c[i];
}
int mx=c[n];
for(int i=n-1;i >= 1;i--) {
c[i]=min(c[i],c[i+1]);
mx+=c[i];
}
for(int i=1;i<=n;i++){
if(c[i]<b[i]){
cout<<"NO\n";
return;
}
}
if(m>=mn && m<=mx){
cout<<"YES\n";
}
else cout<<"NO\n";
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}
2. 性质不同的数字
知识点:离散化,哈希,异或哈希,随机数,阅读理解
首先要看明白题目在问什么,本题难点在于读明白题
对于两个数,如果两个数所处的位置,被完全相同的一些线段覆盖,则性质相同,反之性质不同
对于样例一,在 \([1,6]\) 区间中可以选一个数,在其他地方可以选一个数,这两个数性质不同。
对于样例二,最多选出 \(6\) 个数: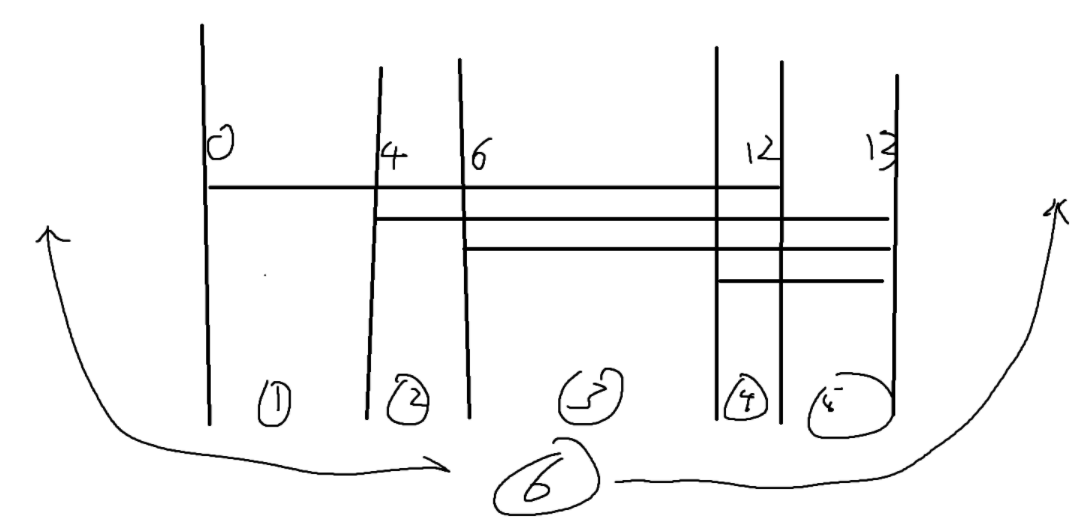
所以我们只要让不同组合的区间拥有不同的值,统计值的种类数量即可
在样例二中,不同组合的区间有五个,分别是:\([0,3],[4,5],[6,11],[12,12],[13,13]\),再加上两侧没有被覆盖的地方,一共六种组合
如何让每个组合有不同的值?
可以给所有的线段一个随机值,让每个点的值等于所有覆盖这个点的线段的随机值异或和,类似于哈希的思想。
最后统计不同值的数量即可
注意需要离散化
#include<bits/stdc++.h>
#define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e18;
const int mod = 998244353;
void solve(){
int n;
cin>>n;
if(n==0){
cout<<1<<endl;
return;
}
vector<pii> seg(n+1);
vector<int> a;
for(int i=1;i<=n;i++){
int l,r;
cin>>l>>r;
a.push_back(l);
a.push_back(r+1);
seg[i]={l,r};
}
sort(a.begin(),a.end());
a.erase(unique(a.begin(),a.end()),a.end());
map<int,int> pos;
for(int i=0;i<a.size();i++){
pos[a[i]]=i+1;
}
vector<ull> d(n*2+10);
std::mt19937_64 rng(std::random_device{}());
std::uniform_int_distribution<uint64_t> dist(0, std::numeric_limits<uint64_t>::max());
for(int i=1;i<=n;i++){
int l=pos[seg[i].first];
int r=pos[seg[i].second+1];
ull rdm=dist(rng);
d[l]^=rdm;
d[r]^=rdm;
}
for(int i=1;i<d.size();i++){
d[i]^=d[i-1];
}
set<ull> set;
for(auto val:d){
set.insert(val);
}
cout<<set.size()<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}
3. 1008 01环
对于合法的序列 \(t\),可以认为是 \(010101\) 这样的
对于 \(s\) ,\(f[i]=(s[i]==t[i])\)
换句话说,\(f\) 数组记录的是每个位置的数是否正确
如果 \(f\) 数组是全 1 或全 0,则答案分别为 0 和 n/2
否则,需要把 \(f\) 中所有的 \(0\) 变成 \(1\),最优方式是,对于每一段长度为 \(x\) 连续的 \(0\),花费 \((x+1)/2\) 次变化
#include<bits/stdc++.h>
// #define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e9;
const int mod = 998244353;
void solve(){
int n;
cin>>n;
string s;
cin>>s;
int ans=inf;
vector<int> a(n);
for(int i=0;i<n;i++){
a[i]=(s[i]=='1');
}
auto work=[&]()->void {
int tmp=0;
vector<int> tar(n);
for(int i=0;i<n;i++){
if(i&1) tar[i]=1;
}
int sum=0;
for(int i=0;i<n;i++){
tar[i]=(tar[i]==a[i]);
sum+=tar[i];
}
if(sum==n){
ans=0;
return;
}
if(sum==0){
ans=min(ans,(n+1)/2);
return;
}
int start=0;
while(!tar[start]) start++;
int cnt=0;
for(int i=0;i<n;i++){
int pos=(i+start)%n;
if(tar[pos]==0){
cnt++;
}
else if(tar[pos]==1){
tmp+=(cnt+1)/2;
cnt=0;
}
}
tmp+=(cnt+1)/2;
ans=min(tmp,ans);
};
work();
for(int i=0;i<n;i++){
a[i]=(s[i]=='0');
}
work();
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}
4. 1012 核心共振
知识点:切比雪夫距离,曼哈顿距离等距离的转化
定义新坐标系:
\(u_i=x_i+y_i,~v_i=x_i-y_i\)
又因为:
\(max(|a|,|b|)=1/2 * (|a+b| +|a-b|)\) (核心公式,可以手算一下正确性)
所以:
\(max(∣x_i−x_j∣,∣y_i−y_j∣)=1/2 * (∣u_i−u_j∣+∣v_i−v_j∣)\)
带入得到:
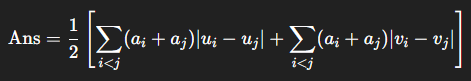
定义:
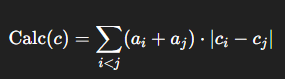
则:
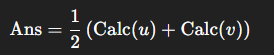
对于计算 \(Calc(c)\),对每个点按照 \(c\) 值排序,得到:
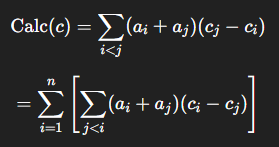
拆分后得到:
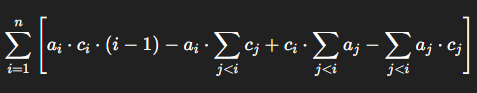
分别维护 \(c_i,a_i,c_i*a_i\)的前缀和,计算每个点对答案的贡献即可
#include<bits/stdc++.h>
#define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e18;
const int mod = 1e9+7;
const int inv2=(mod+1)/2;
void solve(){
int n;
cin>>n;
vector<pii> a(n+1),b(n+1);
for(int i=1;i<=n;i++){
int x,y,val;
cin>>x>>y>>val;
a[i]={x+y,val};
b[i]={x-y,val};
}
auto work=[&](vector<pii> &t)-> int {
sort(t.begin()+1,t.end());
vector<int> su(n+1),sval(n+1),suval(n+1);
int res=0;
for(int i=1;i<=n;i++){
su[i]=su[i-1]+t[i].first;
sval[i]=sval[i-1]+t[i].second;
suval[i]=suval[i-1]+t[i].first*t[i].second;
su[i]=(su[i]%mod+mod)%mod;
sval[i]=(sval[i]%mod+mod)%mod;
suval[i]=(suval[i]%mod+mod)%mod;
}
for(int i=1;i<=n;i++){
res+=t[i].first*t[i].second%mod*(i-1);
res=(res%mod+mod)%mod;
res-=t[i].second*su[i-1];
res=(res%mod+mod)%mod;
res+=t[i].first*sval[i-1];
res=(res%mod+mod)%mod;
res-=suval[i-1];
res=(res%mod+mod)%mod;
}
return res*inv2%mod;
};
int ans=0;
ans+=work(a);
ans+=work(b);
ans%=mod;
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号