2025“钉耙编程”中国大学生算法设计暑期联赛(1)01/03/05/06/07/09/10
难度排序
1. 1010 中位数
知识点:优化枚举,动态维护中位数
两种做法
- 枚举区间中点+动态维护中位数,复杂度 n^2*logn(正常来说会TLE)
- 枚举每个数作为中位数时的贡献,复杂度 n^2
第一种做法
复杂度2000 * 2000 * 20 * log2000,大概 8e8 的复杂度,如果使用大常数的数据结构,例如多重集和优先队列动态维护中位数,会TLE
但因为树状数组天生的超级小常数,导致使用树状数组维护中位数的速度飞快,具体来说:
树状数组写法就比较无脑,每次我们枚举区间的终点 mid
则 [mid-1, mid+1], [mid-2, mid+2], ...... , [mid-k, mid+k]都是一个以 mid 为中点的序列
在序列每次变大时,将新加进来的数放入树状数组,查询中位数,累加答案即可
注意如果在树状数组上朴素的查询中位数,复杂度是 log*log 的,但是有方法可以在单 log 的时间下,在树状数组上查询第k大值
注意这个做法不是正解,只是被优秀的卡常技巧卡过去了
第二种做法(正解)
枚举每个数作为中位数时的答案:
当 a[i] 作为中位数时,枚举 j :从 i 到 n
设数组p,含义是:如果 a[j] > a[i] 则 p[j] = 1, a[j] < a[i] 则 p[j] = -1
求得 i~n 的p数组后,对 p[i~n] 做前缀和,设前缀和数组为pre[j]。
步骤1:则此时 pre[j] 表示:区间 i ~ j 还需要 pre[j] 个比 a[i] 小的数才能使得 a[i] 为区间中位数,假设 t=pre[i]
步骤2:我们用相同的方法,在区间 1~i 上,找到满足 j :1~i,a[j] ~ a[i] 恰好需要 t 个比 a[i] 大的数。
此时,这步骤1,2的两个 j ,正好是一个以 a[i] 作为中位数的合法区间。累加答案即可
代码非常简单好写,甚至不用创建新数组
正解代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e18;
const int mod = 998244353;
void solve(){
int n;
cin>>n;
vector<int> a(n+1);
for(int i=1;i<=n;i++){
cin>>a[i];
}
int ans=0;
for(int i=1;i<=n;i++){
//枚举a[i]做为中位数
vector<int> cnt(n+2010);
int now=0;
for(int j=i;j<=n;j++){
if(a[j]>a[i]) now++;
else if(a[j]<a[i]) now--;
cnt[now+2000]+=j;
}
now=0;
for(int j=i;j>=1;j--){
if(a[j]<a[i]) now++;
else if(a[j]>a[i]) now--;
ans+=j*cnt[now+2000]*a[i];
}
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}
树状数组代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e18;
const int mod = 998244353;
struct TreeArray {
int n;
vector<ll> tr;
TreeArray(int _n) { init(_n); }
TreeArray() {}
// 初始化,开辟大小为 n+1 的数组,下标从 1 开始使用
void init(int _n) {
n = _n;
tr.assign(n + 1, 0);
}
// lowbit 函数,获取最低位的 1
inline int lowbit(int x) {
return x & -x;
}
// 在下标 x 增加值 c
void insert(int x, ll c) {
for (int i = x; i <= n; i += lowbit(i)) {
tr[i] += c;
}
}
// 获取前缀和 [1..x]
ll sum(int x) {
ll ans = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
ans += tr[i];
}
return ans;
}
ll query(int l,int r){
return sum(r)-sum(l-1);
}
// 二分查找:返回最大的 x,使得 sum(x) <= k
// 如果所有前缀和都大于 k,则返回 0
int select(ll k) const {
int x = 0;
ll cur = 0;
// i 从最高 2^⌊lg n⌋ 开始
for (int i = 1 << (31 - __builtin_clz(n)); i > 0; i >>= 1) {
if (x + i <= n && cur + tr[x + i] <= k) {
x += i;
cur += tr[x];
}
}
return x;
}
int kth(int k) const {
int pos = 0, bit = 1<<11;
// 2^11 = 2048 > 2000,上界可稍微放大
for (; bit; bit >>= 1) {
int np = pos + bit;
if (np <= n && tr[np] < k) {
k -= tr[np];
pos = np;
}
}
return pos + 1;
}
};
void solve(){
int n;
cin>>n;
vector<int>a(n+1);
for(int i=1;i<=n;i++){
cin>>a[i];
}
ll ans=0;
for(int mid=1;mid<=n;mid++){
TreeArray tr(2000);
tr.insert(a[mid],1);
int med=a[mid];
vector<int> cnt(n+1);
cnt[med]=1;
int l=0,r=0;
ans+=mid*mid*med;
int maxk=min(mid-1,n-mid);
for(int k=1;k<=maxk;k++){
tr.insert(a[mid-k],1);
tr.insert(a[mid+k],1);
med=tr.kth(k+1);
ans+=med*(mid-k)*(mid+k);
}
}
cout<<ans<<"\n";
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}
2. 1005 传送门
知识点:图论,最短路,建图,虚点
重点是如何建立可以直接跑最短路的图模型
如果你做过类似的题目,就会很快的发现,做法大概是要建立额外的点,辅助进行最短路
回顾题意,对于连续且所属同一协会的路径,只需要交一次钱即可
假设路径u~v,协会是c
则对点u,建立两个虚点,分别表示:状态{u,c} (id1),状态{v,c} (id2)
连接:
u 到 id1 的路径,边权为1,id1 到 u 的路径,权值为0
v 到 id2 的路径,边权为1,id2 到 v 的路径,权值为0
id1 到 id2 的双向路径,权值为0
建立图后,你会发现,刚好满足题意,对于连续且所属同一协会的路径,只需要交一次钱
而我们建立的虚点,等价于:在一段连续且协会相同的路径上,只需要一次缴费,即可走到由我们自定义的状态表示的点上
而这些点,可以免费到达连续且协会相同的其他状态点,也可以免费下到原图上的点
同时因为是01图,不需要 dijkstra,跑 01BFS 即可
#include<bits/stdc++.h>
#define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e18;
const int mod = 998244353;
struct edge{
int u,v,c;
};
void solve(){
int n,m;
cin>>n>>m;
int tar=n;
vector<vector<pii>> g(2*(n+m+10));
map<pii,int> id;
vector<edge> e;
for(int i=1;i<=m;i++){
int u,v,c;
cin>>u>>v>>c;
if(!id[{u,c}]) id[{u,c}]=++n;
if(!id[{v,c}]) id[{v,c}]=++n;
e.push_back({u,v,c});
}
for(auto [u,v,c]:e){
int id1=id[{u,c}];
int id2=id[{v,c}];
g[u].push_back({id1,1});
g[v].push_back({id2,1});
g[id1].push_back({id2,0});
g[id2].push_back({id1,0});
g[id1].push_back({u,0});
g[id2].push_back({v,0});
}
deque<int> dq;
vector<int> dist(n+1,inf);
dist[1]=0;
dq.push_back(1);
while(!dq.empty()){
int u=dq.front();
dq.pop_front();
for(auto[v,w]:g[u]) {
if(dist[v]>dist[u]+w) {
dist[v]=dist[u]+w;
if(w==0) dq.push_front(v);
else dq.push_back(v);
}
}
}
cout<<dist[tar]<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}
3. 1009 子序列
知识点:优化枚举
从 n 到 1,枚举两端点值中的最小值m。(或者说枚举可选子序列的最大值m,这个是更符合下面说法的)
同时维护所有大于等于m的值的集合p
枚举到m时,将m加入到集合p中,此时两端点一定从p中选,因为不从p中选,则两端点最小值小于m,不符合我们的枚举方式
而如果从p中选,则因为此时最小值是m,所以中间可选的所有值一定小于m,所以一定不会选到集合中的值
所以,最优选法一定是,两端点分别为集合中最靠左的数(位置是l)和最靠右的数(位置是r),子序列长度是:
(r-l+1)- p.size + 2
r-l+1 是区间长度,减去 p.size 是因为这些数都不可选,+2是两端点
#include<bits/stdc++.h>
#define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e18;
const int mod = 998244353;
void solve(){
int n;
cin>>n;
vector<int> a(n+1),pos(n+1);
for(int i=1;i<=n;i++){
cin>>a[i];
pos[a[i]]=i;
}
if(n==1){
cout<<1<<endl;
return;
}
int ans=1;
int r=0,l=n+1;
int cnt=0;
for(int i=n;i>=1;i--){
//枚举两个端点的最小值为i的情况
cnt++;
r=max(r,pos[i]);
l=min(l,pos[i]);
if(cnt>=2){
ans=max(ans,(r-l+1)-cnt+2);
}
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}
4. 1006 景区建设
知识点:好像没啥知识点,硬要说的话能沾上点最小生成树
首先对于每一个“山峰”和(1,1),必须要建立传送器。同时因为建立传送器的代价很大,所以一定是要最小化建立传送器的数量。
所以传送器的数量可以确定,就是山峰的数量,同时还需要包含(1,1)
然后就是在这些传送器之间,建立路径(最小生成树),使得传送器全联通。
路径的代价是:
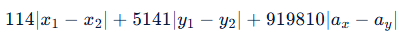
即使 x1 和 x2的差值加上 y1 和 y2 的差值拉到最大,也不大与919810,所以影响建立路径的唯一因素是高度差。
所以对所有传送器按照高度排序,相邻的传送器之间建立路径即可
#include<bits/stdc++.h>
#define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e18;
const int mod = 998244353;
struct node{
int x,y,h;
};
void solve(){
int n,m;
cin>>n>>m;
vector<vector<int>> g(n+1,vector<int>(m+1));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>g[i][j];
}
}
vector<node> t;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
bool f=1;
if(i>1 && g[i][j]<g[i-1][j]) f=0;
if(i<n && g[i][j]<g[i+1][j]) f=0;
if(j>1 && g[i][j]<g[i][j-1]) f=0;
if(j<m && g[i][j]<g[i][j+1]) f=0;
if(i==1 && j==1) f=1;
if(f){
t.push_back({i,j,g[i][j]});
}
}
}
int ans=(1ll<<34)*(t.size()-1);
sort(t.begin(),t.end(),[&](node t1,node t2){
return t1.h<t2.h;
});
for(int i=1;i<t.size();i++){
ans+=abs(t[i].h-t[i -1].h)*919810;
ans+=abs(t[i].y-t[i-1].y)*5141;
ans+=abs(t[i].x-t[i-1].x)*114;
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}
5. 1007 树上LCM
知识点:SOSDP,分解质因数,LCM
题解1:
首先对于 X,可以分解成很多个质因数的几次方相乘的形式,例如 504 = 2^3 * 3^2 * 7^1
而对于 X 的数据范围,最多大概是7~8种不同的质因数相乘,设 X 不同的质因数个数为 k
把每个节点的值压缩成 k 位二进制形式:
假设 X 的第 i 个质因子的值为 val,出现次数为 cnt,则可以表示为:val^cnt 的形式
对于 a[u],如果也存在因子 val,且出现次数恰好等于 cnt,则 a[u] 对应的二进制值的第 i 位为 1
如果 a[u] 存在因子 val 但出现次数大于 cnt,或者 a[u] 有 X 中不存在的因子,则直接给 a[u] 的二进制值改成 -1,表示 a[u] 不能出现在任何一条路径中
(因为在这两种情况下,任何数与 a[u] 的 LCM 不可能等于 X)
将每个数转换为二进制掩码后,开始计算路径数量
对于节点 u,子节点为 v1, v2, v3, ... vi
可能的路径一共有三种:
- 以 u 为上端点,另一端点在子节点的子树内部
- 两端点都在子节点的子树内部,且路径会跨越 u
- u->u 的一条路径 (节点自身)
设 f[u] [mask] 表示:以u为一个端点,另一个端点在子树内部,路径的掩码或起来为 mask 的路径数量
对于一条合法的路径,等价于路径的 mask 或值 == (1<<k)-1
对子节点 vi,计算 u 的第2种路径时,分为两步:
- 先枚举 vi 子树内的所有以 vi 为一个端点的路径掩码 mask1,我们要找到其他子树 v1 到 v(i-1) 连接到 u 后(情况 1 的路径),路径掩码 mask2 与 mask1 或起来为(1<<k)-1的路径数量。
我们可以计算出 mask2 的值,mask2 为 (mask1 ^ (1<<k)-1) 的超集。所以对于 f[vi][mask1],符合条件的可连接路径情况2数量为:f[u] 中((mask1 ^ (1<<k)-1)的所有超集之和,这一步可用 sosdp 计算 - 计算完情况2的路径后,再将 f[v1] [mask] 合并到 u上,更新 f[u] [mask],统计情况1路径的同时为下一个子节点 v(i+1) 的情况2路径统计做准备
整个过程用 DFS 维护即可,单点复杂度:k *(2^k),总体复杂度n * k *(2^k)
题解2:
对 \(x\) 分解质因数,可以分解为最多不超过 8 个质因数相乘。
我们设 \(x\) 的质因子个数为 \(k\) 个,然后把每个节点 \(a_i\) 的值状压成一个二进制数:
如果 \(a_i\) 的某个质因子 \(t\) 出现次数与 \(x\) 的 \(t\) 出现次数相等,则将这一位修改为 \(1\)
若 \(a_i\) 的某个质因子 \(t\) 出现次数小于 \(x\) 的 \(t\) 出现次数,则将这一位修改为 \(0\)
若 \(a_i\) 的某个质因子 \(t\) 出现次数大于 \(x\) 的 \(t\) 出现次数,则将这一位修改为 \(-1\),\(-1\) 代表这个点不能在 \(LCM\) 路径上,因为不可能 LCM 出 \(X\)
若 \(a_i\) 的某个质因子 \(t\) 在 \(x\) 中没有出现过,则将这一位修改为 \(-1\)
然后 \(dfs\) 整棵树
设 \(f[u][j]\) 表示:以 \(u\) 为一个端点,另一个端点在子树内部,路径的掩码或起来为 \(j\) 的路径数量
\(dfs\) 节点 \(u\)时,找到所有子节点 \(v\) 内部的 \(f[v][mask]\)
再把 \(f[v][mask]\) 合并到 \(u\) 上
合并时,假设子树 \(v\) 内有个掩码为 \(mask\) 的路径
则这个路径可以和 \([(mask~~xor~~((1<<k)-1))]\) 这个掩码 \(|\) 来得到 \([1<<k-1]\)
\([(mask~~xor~~((1<<k)-1))]\) 表示 \(mask\) 对 \(full mask~~((1<<k)-1)\) 的补集
同时,还可以和 \((mask~~xor~~((1<<k)-1))\) 的所有超集,\(|\) 得到 \([1<<k-1\)]
所以这里可以使用超集和DP(SOSDP的变形)来得到超集之和
统计完子树 \(v\) 的答案后再将 \(f[v]\) 合并到 \(f[u]\) 中
#include<bits/stdc++.h>
#define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e18;
const int mod = 998244353;
int lcm(int a,int b){
return a*b/__gcd(a,b);
}
//先处理出x的质因数和个数
//dfs每个点u,找到所有v内部的f[mask]
//再把fv[mask]合并到u上
//合并时,假设子树v内有个掩码为mask的路径
//则这个路径可以和: (mask^((1<<k)-1)) 这个掩码|起来得到1<<k-1
//但同时,还可以和(mask^((1<<k)-1))的所有超集,|得到1<<k-1
//所以可以使用高维前缀和,sosdp
void solve(){
int n,x;
cin>>n>>x;
vector<vector<int>> g(n+1);
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
vector<int> a(n+1);
for(int i=1;i<=n;i++){
cin>>a[i];
}
map<int,int> cnt;//统计x的质因数对应的个数
//统计cnt
int nx=x;
for(int i=2;i<=nx;i++){
int tmp=0;
while(nx%i==0){
nx/=i;
tmp++;
}
if(tmp) cnt[i]=tmp;
}
if(nx>1){
cnt[nx]=1;
}
int k=cnt.size();//质因数种类数
auto get=[&](int val)-> int {
if(lcm(x,val)!=x) return -1;
int pos=0,res=0;
for(auto [v,c]:cnt){
int now=0;
while(val%v==0){
now++;
val/=v;
}
if(now==c) res|=(1<<pos);
pos++;
}
return res;
};
for(int i=1;i<=n;i++){
a[i]=get(a[i]);// 将a[i]转换为与x的质因数对应的掩码
}
int ans=0;
//以u为一个端点,另一个端点在子树内部,路径的掩码或起来为j的路径数量
vector<vector<int>> f(n+1,vector<int>(1<<k));
auto dfs=[&](auto dfs,int u,int pre)->void {
for(auto v:g[u]){
if(v==pre) continue;
dfs(dfs,v,u);
}
if(a[u]==-1) return;
f[u][a[u]]=1;
for(auto v:g[u]){
if(v==pre) continue;
//计算超集和
auto s=f[u];
for(int j=0;j<k;j++){
for(int i=0;i<(1<<k);i++){
if(!(i>>j&1)){
s[i]+=s[i^(1<<j)];
}
}
}
for(int i=0;i<(1<<k);i++){
int val=i|a[u];
ans+=s[val^((1<<k)-1)]*f[v][i];
f[u][val]+=f[v][i];
}
}
//之前只统计了,从子树v连接上去的路径,没有统计单个节点的
if(a[u]==(1<<k)-1) ans++;
};
dfs(dfs,1,0);
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}
6. 1003 奸商
知识点:二进制枚举,SOSDP
所有长度为奇数的字符串一定优秀
若所有长度为 \(n\) 且 \(n\) 为偶数的子串优秀,则所有长度大于 \(n\) 且是偶数的子串优秀
所以只要保证所有最短的偶数子串优秀即可
最短的长度是 \(len\),若 \(len\) 是奇数,则 \(len++\)
将所有长度为 \(len\) 的子串,幻视需求表达为一个 \(17\) 位二进制数,若将 \('a'+i\) 幻视后,子串可以变优秀,则第 \(i\) 位修改为 \(1\),否则为 \(0\)
我们需要找到一个方案,让所有的需求,至少有一个被改为 \(1\) 的位进行幻视
暴力做法:
枚举 \(0 ~到~ (1<<17-1)\) 的所有方案,若某个方案可以满足所有需求,则这个方案可以作为备选,复杂度 \(n * (1<<17) == 4e8\)
SOSDP做法:
设需求 \(m\) 对于全集的补集 \(t\)
如果修改方案为 \(t\) 或 \(t\) 的子集,则需求 \(m\) 不能被修改到,所以方案 \(t\) 和 \(t\) 的子集不能做为备选方案
所以对每个需求 \(m\),可以找到一个 \(t\),将 \(t\) 标记为 \(false\),再使用超集和DP,将 \(t\) 的所有子集也标记为 \(false\),其他没被标记的集合可作为备选
复杂度\(17 * (1<<17)\)
#include<bits/stdc++.h>
#define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e18;
const int mod = 998244353;
void solve(){
int n;
cin>>n;
string s;
cin>>s;
s=" "+s;
vector<int> w(200);
for(int i=0;i<17;i++){
int val;
cin>>val;
w['a'+i]=val;
}
int len;
cin>>len;
if(len&1) len++;
vector<int> nd;
for(int i=1;i<=n-len+1;i++){
int mask=0;
for(int l=i,r=i+len-1;l<r;l++,r--){
if(s[l]==s[r]){
mask=0;
break;
}
else{
int k=l;
if(s[r]<s[l]) k=r;
mask|=1<<(min(s[l]-'a',s[r]-'a'));
}
}
if(mask){
nd.push_back(mask);
}
}
//到这里开始,sosdp或暴力
//要从0~(1<<17)中找一个方案,使得方案|上任何一个nd的结果都不为0
//暴力做法复杂度nd.size()(==3000) * (1<<17) == 4e8
int ans=inf;
if(nd.size()==0) ans=0;
// for(int i=0;i<(1<<17);i++){
// int cost=0,f=1;
// for(auto m:nd){
// if(!(i&m)){
// f=0;
// break;
// }
// }
// if(f){
// for(int k=0;k<17;k++){
// if(i>>k&1) cost+=w['a'+k];
// }
// ans=min(ans,cost);
// }
// }
// cout<<ans<<endl;
//sosdp做法,对于所有nd的补集t,标记为false
//然后做超集和dp,剔除掉所有t的子集
vector<int> f(1<<17,1);
for(auto m:nd){
f[m^((1<<17)-1)]=0;
}
for(int j=0;j<17;j++){
for (int mask=0;mask<(1<<17);mask++){
if(!(mask>>j&1)){
f[mask]&=f[mask^(1<<j)];
}
}
}
for(int mask=0;mask <(1<<17);mask++){
if(!f[mask]) continue;
int cost=0;
for(int k=0; k<17;k++){
if(mask & (1<<k)) cost+=w['a'+k];
}
ans=min(ans,cost);
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}
7. 1001 博弈
知识点:博弈论,nim游戏,反nim游戏,组合数学
(前置知识是 \(nim\) 和 \(anti-nim\) 的结论以及组合数学)
每个房间可以看成是一个 \(nim\) 游戏或一个反 \(nim\) 游戏
称先手为 \(A\),后手为 $B
看成 \(nim\) 游戏时:
异或和非零:则 \(A\) 可以让下一个房间B先手
异或和为零:则 \(B\) 可以让下一个房间A先手
看成反 \(nim\) 游戏时:
若所有堆都是 \(1\),且堆的数量是偶数,则下一个房间 \(A\) 先手
若至少一堆大于 \(1\),且异或和非零,则 \(A\) 可以让下一个房间 \(A\) 先手
其余情况,\(B\) 可以让下一个房间B先手
\(nim\) 和 \(anti-nim\) 的结果是确定的
所以每个房间都是以下四种结果之一:
- \(A\) 可以让下个房间B先手,\(A\) 可以让下个房间自己先手
- \(B\) 可以让下个房间A先手,\(B\) 可以让下个房间自己先手
- \(A\) 可以让下个房间B先手,\(B\) 可以让下个房间自己先手
- \(A\) 可以让下个房间自己先手,\(B\) 可以让下个房间自己先手
对于结果1,2
结果1:如果到这个房间,则 \(A\) 必胜
结果2:如果到这个房间,则 \(B\) 必胜
结果3:到这个房间,一定会交换下一个房间的先后手顺序
结果4:一定不会交换下一个房间的先后手顺序
总结归纳房间类型:
a:先手可以决定下一个房间的先后手
b:后手可以决定下一个房间的先后手
c:先后手交换顺序
d:先后手顺序不变
排列组合 \(Alice\) 赢的情况:
一.\(a\) 或 \(b\) 不为0的情况
- 前面有偶数个 \(c\),然后放一个 \(a\),剩下的 \(a,b\) 随便放( \(d\) 先不考虑,因为 \(d\) 对答案完全没影响)
- 前面有奇数个 \(c\) ,然后放一个 \(b\) ,剩下的 \(a,b\) 随便放
- 累加这两种情况,再乘上 \(C(n,d)*d!\)
二.\(a\) 和 \(b\) 都为 \(0\) 的情况
\(c\) 是偶数时答案为 \(n!\) ,否则答案为 \(0\)
#include<bits/stdc++.h>
#define int long long
using namespace std;
using pii=pair<int,int>;
using ll = long long;
using ull = unsigned long long;
//using i128 = __int128_t;
const ll inf = 1e18;
const int mod = 1e9+7;
const int N=1e6;
int fact[N+1],infact[N+1];
int qmi(int a,int b,int p){
int res=1;
while(b){
if(b&1) res=res*a%p;
b>>=1;
a=a*a%p;
}
return res;
}
// 组合数计算 C(n, k)
ll C(int a,int b){
if(a<0 || b<0 || b>a) return 0;
return fact[a]*infact[b]%mod*infact[a-b]%mod;
}
void init(){
fact[0]=1;
infact[0]=1;
for (int i=1;i<=N;i++){
fact[i]=fact[i-1]*i%mod;
}
infact[N]=qmi(fact[N],mod-2,mod);
for(int i=N-1;i>=1;i--){
infact[i]=infact[i+1]*(i+1)%mod;
}
}
void solve(){
int n;
cin>>n;
int a=0,b=0,c=0,d=0;
for(int i=1;i<=n;i++){
int k,val,sum=0;
cin>>k;
bool f=1;//是否全0
for(int j=1;j<=k;j++){
cin>>val;
sum^=val;
if(val!=1) f=0;
}
bool A=0;
if(f && !(k&1)) A=1;
else if(!f && sum) A=1;
if(sum && A) a++;
else if(!sum && !A) b++;
else if(sum && !A) c++;
else d++;
}
int ans=0;
if (a==0 && b==0){
if(c&1) cout<<fact[n]<<endl;
else cout<<0<<endl;
return;
}
/*
1. 前面有偶数个c,然后放一个a,剩下的ab随便放(d先不考虑,因为d对答案完全没影响)
2. 前面有奇数个c,然后放一个b,剩下的ab随便放
累加这两种情况,再乘上C(n,d)*d!
*/
for(int i=0;i<=c;i+=2){
ans+=C(c,i)*fact[i]%mod*a%mod*fact[n-d-1-i]%mod;
ans%=mod;
}
for(int i=1;i<=c;i+=2){
ans+=C(c,i)*fact[i]%mod*b%mod*fact[n-d-1-i]%mod;
ans%=mod;
}
ans*=C(n,d)*fact[d]%mod;
ans%=mod;
cout<<ans%mod<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
init();
int ct=1;
cin>>ct;
while(ct--){
solve();
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号