莫队学习笔记

莫队

略过不讲

带修莫队

适用情况:

  • 带修改的区间查询，修改可做到\(O(1)\)

算法概要

在莫队基础上加上一位记录当前的时间(即当前询问之前进行了几次修改),查询的过程中前后调整即可

例题

树上莫队

适用情况:

  • 在树上的区间查询
  • 支持修改

算法概要(1)

通过括号序或者欧拉序将树压成一个序列，转而进行莫队。

实现(1)

先预处理括号序，记录两个数组\(in,out\),分别存储\(u\)靠前的和靠后的括号序
对于当前询问\(x,y(in_x<in_y)\),分类讨论

  • \(lca=x\),将询问转化为\([in_x,in_y]\)
  • \(lca!=x\),将询问转化为\([out_x,in_y]\)加上\(lca\)的贡献

下面讲一下上述方案的正确性
我们可以发现\(1-in_u\)代表\(1-u\)这条链上的全部取了,\(u\)子树上的点都没碰过。
同样\(1-out_u\)代表的也是\(1-u\)这条链上的贡献，但是\(u\)子树上的点都统计了两次，贡献抵消了。
结合前缀和的想法，\([in_x,in_y]\)可以看做从\(x\)这个点往下一直取到\(y\)的贡献之和。
而对于第二种情况，如果我们仍然适用\(in_x\)的话,就会把x子树中的点给算进去，所以应用\(out_u\)。
看图理解(黄色表示括号序,红色表示计算了一次的点，绿色表示计算了两次的点，蓝色表示没访问过的点，当前询问区间为1至5)。

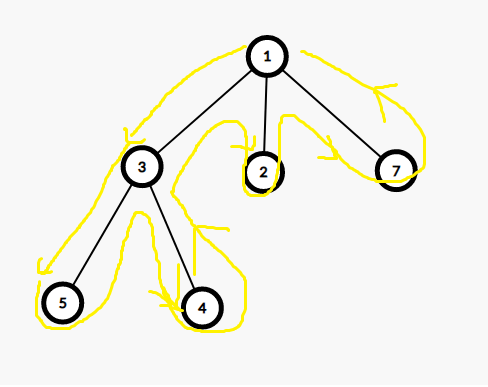
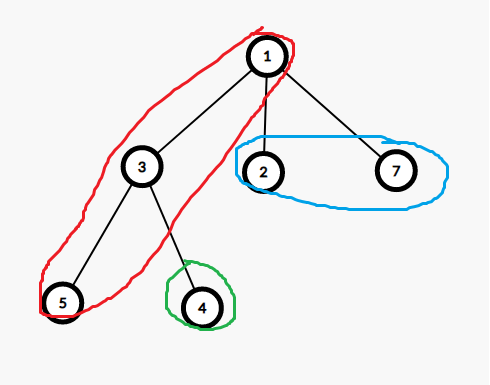
算法概要(2)

可以注意到上面的莫队似乎只是把树变成序列，下面讲一下直接在树上分块的树上莫队

实现(2)

参考[SCOI2005] 王室联邦
本题虽然并非莫队问题，但是提供了一种树上分块的思路、

例题

二次离线莫队

适用情况:

  • 可离线区间查询（即可莫队）
  • 单点更新无法做到 \(O(1)\)

算法概要

简单来说，莫莫就是通过将无法 \(O(1)\) 实现的修改再次离线，通过扫描线实现复杂度的优化（\(O(nk\sqrt{n})\) ->\(O(nk+n\sqrt{n})\)）

实现

具体实现过程中我们讨论端点变化对答案的影响，以右端点右移为例，即\([l,r]\)变为\([l,r+k]\)
令\(f(x,[l,r])\)表示\(x\)对于区间\([l,r]\)的贡献，可以注意到\(f(x,[l,r])=f(x,[1,r])-f(x,[1,l])\)
可以形式化为

$\forall x\in(r+1,r+k)$

求

$f(x,[l,x-1])$
已经可以开始扫描线了
注意到这样的保存下来的询问空间复杂度可以达到\(O(n\sqrt{n})\),是我们无法接受的
我们先根据前文的差分式子对于题意化简\(f(x,[l,x-1])=f(x,[1,x-1])-f(x,[1,l])\)
单变量项\(f(x,[1,x-1])\)显然可以预处理，之后我们要做的就是将\((r+1,r+k)\)放到\(l\)这个点里，在扫描线的过程中进行处理
结合代码理解

for(int i=1,l=1,r=0;i<=m;i++){
    if(l>q[i].l) v[r].emplace_back(q[i].l,l-1,i,1);
    while(l>q[i].l) --l,q[i].ans-=p[l];
    if(r<q[i].r) v[l-1].emplace_back(r+1,q[i].r,i,-1);
    while(r<q[i].r) ++r,q[i].ans+=p[r];
    if(l<q[i].l) v[r].emplace_back(l,q[i].l-1,i,-1);
    while(l<q[i].l) q[i].ans+=p[l],++l;
    if(r>q[i].r) v[l-1].emplace_back(q[i].r+1,r,i,1);
    while(r>q[i].r) q[i].ans-=p[r],--r;
}

例题(后续补题解)

二维莫队(多维莫队)

适用情况

  • 多维区间查询

算法概要

本质就是把莫队的单点修改改为整条链修改

回滚莫队

适用情况

  • 添加易而删除难

算法概要

不删除

实现

实际上就是取缔删除操作,从莫队的分块性质去想，如果我们一次查询只计算所有位于同一个块的\(l\),那么我们就算用暴力,也只会修改\(\sqrt{n}\)次，整体的复杂度也不过是\(O(n)\),完全可以接受，那么方法就出来了。我们每次对左端点所在块相同的点莫一下，然后暴力扫一遍左端点所处块即可

例题

posted @ 2025-06-06 21:58  黑昼白夜  阅读(9)  评论(0)    收藏  举报