[思维题] AT_agc007_f [AGC007F] Shik and Copying String

AT_agc007_f [AGC007F] Shik and Copying String

题意简述

有一个长度为 \(N\) 的字符串 \(S_0\) 。一次操作是形如以下的过程：

• 将 \(S_i\) 变换为 \(S_{i+1}\)，其中 \(S_{i+1,1} = S_{i,1}\), \(\forall\ j \in [2,N], S_{i+1,j} = S_{i,j}\) 或 \(S_{i+1,j-1}\)。

求出最少需要多少次操作可以使得 \(S_0\) 变成目标串 \(T\)。

分析

典型的AGC风格的思维题。第一步首先需要观察，不难看出操作的本质相当于用 \(S_0\) 当中的一个字符去对应地覆盖 \(T\) 当中的一个区间。然后注意到这样的覆盖会使得原串的一些位置丢失掉它们本来的字符，所以如果 \(S\) 串中有两个字符 \(c_1, c_2\) （其中 \(c_1\) 位置在前）都需要去覆盖，且 \(c_1\) 所要覆盖的区间的下标范围包含 \(c_2\) 所在位置，那么 \(c_2\) 的覆盖就必须在 \(c_1\) 前面。如果设 \(f_i\) 表示从后往前，一直到完成 \(i\) 的覆盖所需的最小次数，那么 \(f_i = max_{j \in [i,R_i]} \ f_j\)。那么很自然地可以想到从后往前模拟这一过程，于是就，做完了？

假穿了！！！考虑以下情况（图搬自 command_block 题解，隔空感谢）

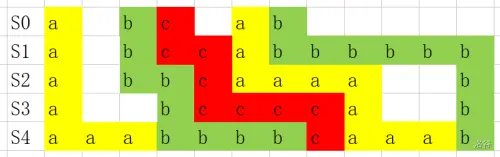
图上 \(S_0\) 中位置 \(1\) 的 \(a\) 字符所覆盖的区间包含位置 \(3\) 的 \(b\) 字符，但是 \(a\) 并不需要在 \(b\) 之后去覆盖！那么就必须从其他角度来分析该如何做这个贪心：

不难发现点对于区间的覆盖相当于在一个二维平面上走一条路径，最优的做法是使得每条路径尽量靠右走（给它左边的路径留空间）直到当前所在横坐标与最后要覆盖的区间左端点相等，然后直到最后一行再横着涂过去覆盖。

接下来考虑维护这一过程。发现图中关键位置是每一次往右走的拐点（这条路径左下方一格就是它左边那条路径经过这个位置的拐点。那么对于要经过一个横坐标值的所有路径，它们的拐点每次都往左下移一格，而纵坐标的意义恰好就是操作的次数，这样就可以计算答案了！于是可以考虑用队列维护这一过程，具体见代码（结合图示多想一想应该可以理解）：

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n;
string s,t;

signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>s>>t;
    if(s.size()!=t.size()){
        cout<<"-1"<<endl; return 0;
    }
    if(s==t){
        cout<<0<<endl; return 0;
    }
    s=" "+s,t=" "+t;
    queue<int> q; int ans=0;
    for(int i=n,pos=n;i>=1;i--){
        while(i-1>=1&&t[i]==t[i-1]) i--;
        while(pos>=1&&(pos>i||s[pos]!=t[i])) pos--;
        if(!pos){
            cout<<"-1"<<endl; return 0;
        }
        while(!q.empty()&&q.front()-q.size()>=i) q.pop(); //队列维护的关键就在这一行！
        if(pos!=i) q.push(pos);
        ans=max(ans,(int)q.size()+1);
    }
    cout<<ans<<endl;
    return 0;
}

总结

本题最重要的一点是把覆盖操作转化为走二维平面上的路径，然后通过路径的向右拐点直观地体现出这一贪心的过程以及路径之间的影响关系（因为不同覆盖可以同时进行，不一定要等后面的覆盖完了再覆盖前面的），再次体现了直观的力量。