第十周作业
20182313 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结
教材学习内容总结
- 图(结点和结点之间的连接构成)
- 顶点：结点
- 边：结点之间的连接
- 邻接：两个结点之间有一条连通边，则两个结点是邻接的，有时邻接顶点称为邻居。
- 自循环(环)：连通一个顶点及其自身的边
- 环路：一种首顶点和末顶点相同且没有重边的路径，没有环路的图称为无环的。
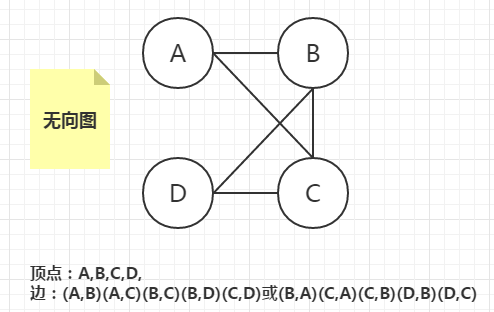
- 无向图
- 无向图是一种边为无序结点对的图。在无向图中，(A,B)(B,A)指的是一条边，表示A与B之间有一条两个方向都连通的边。
- 完全：一个无向图是完全的，说明对于有n个顶点的无向图，图中有n(n-1)/2条边。
- 连通：如果无向图中的任何两个顶点之间都存在一条路径，则认为该无向图是连通的。
- 同时连通还分为强连通和弱连通（非强连通），强连通图中，任何两个顶点之间都是连通的，就是说任何两个顶点之间都至少有一条路径。
- 完全图一定是连通图，连通图不一定是完全图。
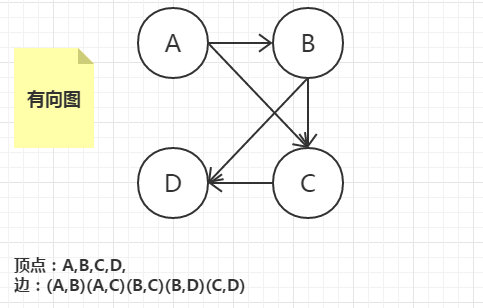
- 有向图
- 有向图/双向图是一种边为有序顶点对的图。在无向图中，(A,B)(B,A)指的不是一条边，(A,B)表示从A到B有一条连通的边，但B到A没有
- 如果有向图中没有环路，且有一条从A到B的边，则可以把顶点A安排在顶点B之前，这种排列得到的顶点次序称为拓扑序
- 有向树：其中一个元素被指定为树根的有向图称为有向树。
- 图的算法
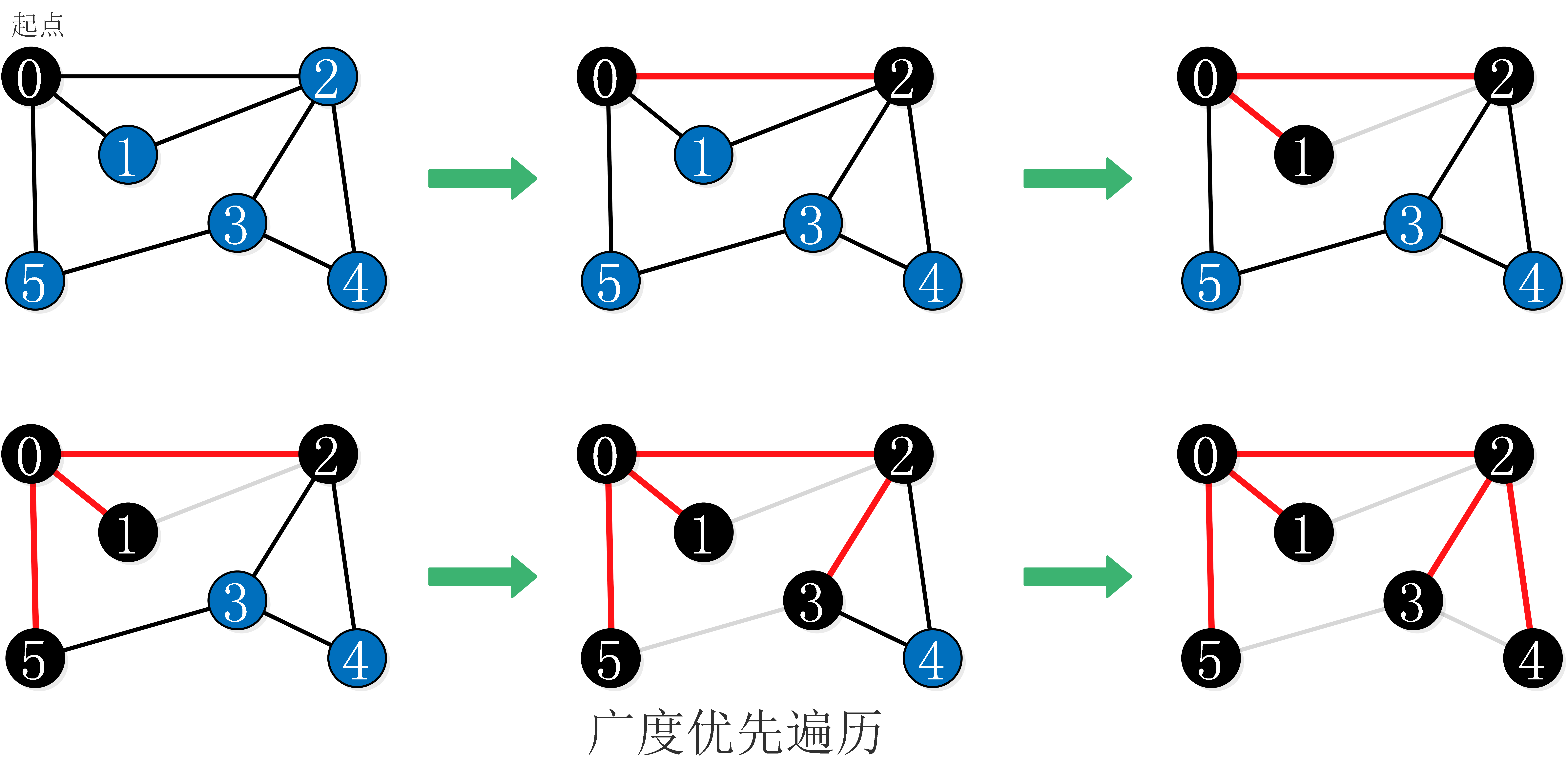
- 图的遍历分为两种：广度优先遍历（简称BFS，与树中的层序遍历类似）深度优先遍历（简称DFS，与树中的前序遍历类似）。
- 广度优先遍历——使用一个队列和一个无序列表来实现，队列用于管理遍历，无序列表用于存储遍历结果。
- 第一步：起始顶点进入队列，标记为已访问。
- 第二步：从队列中取出起始顶点加入无序列表的末端，让与该顶点相连的还未被标记为已访问的顶点加入队列中，把它们都标记为已访问。
- 第三步：重复第二步的操作，每次取出队列中的首个顶点加入无序列表，直至队列为空。
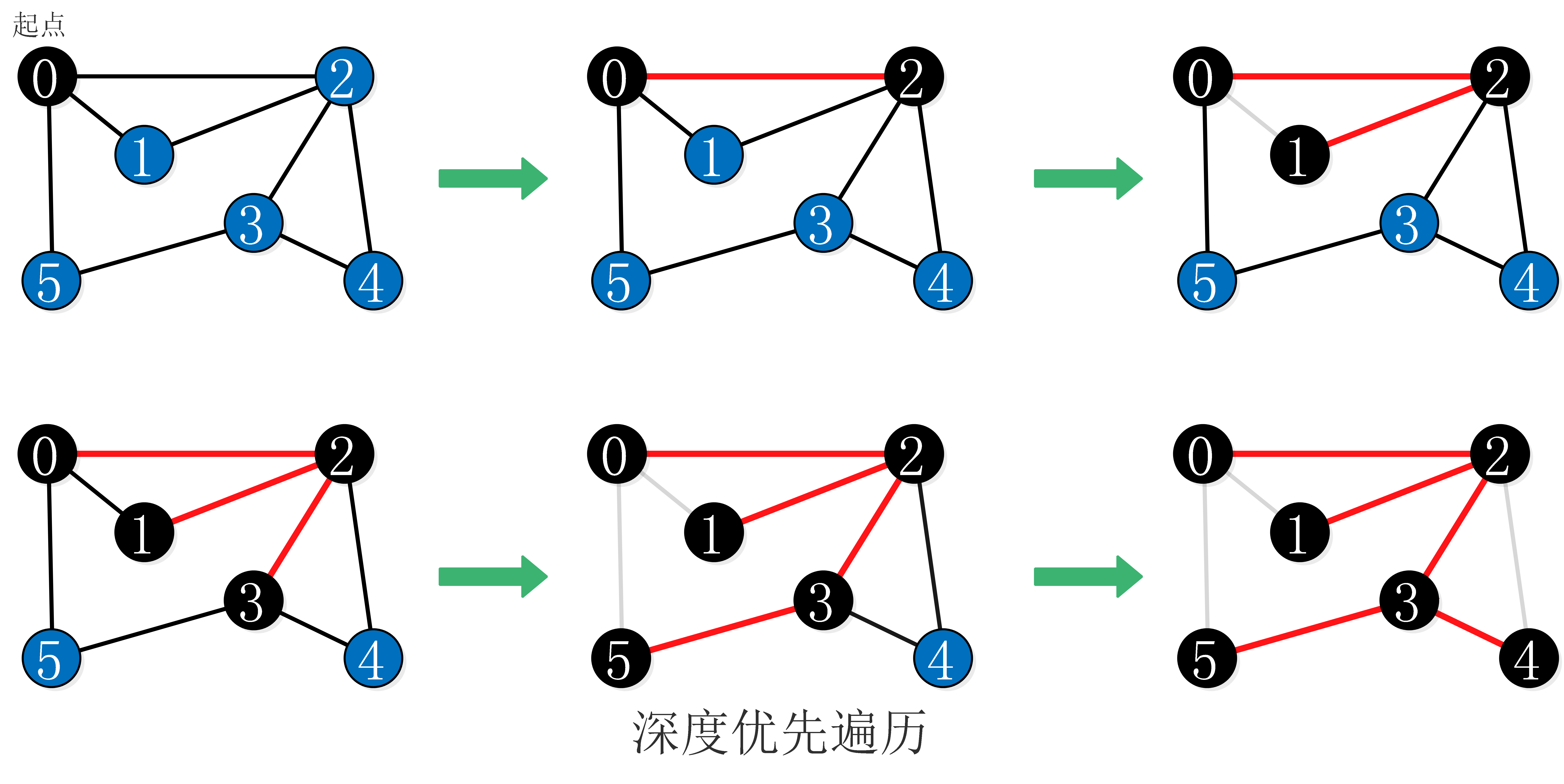
- 深度优先遍历——使用一个栈和一个无序列表来实现，栈的作用与广度优先遍历中队列的作用相同。
- 第一步：起始顶点进入栈。
- 第二步：从栈中取出起始顶点加入无序列表的末端，标记为已访问，让与该顶点相连的顶点加入栈中。
- 第三步：重复第二步的操作，每次取出栈顶元素加入无序列表，把顶点标记为已访问，直至栈为空。
- 图的实现策略
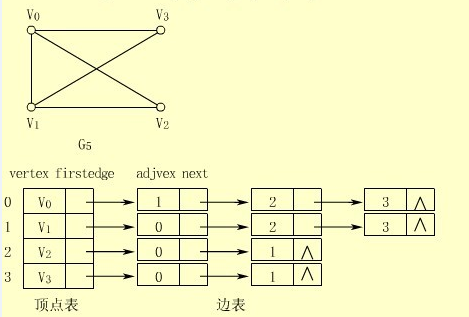
- 邻接列表是一种特殊的链表，它的图样类似于哈希排序中的链地址法，顶点存储在一个列表中，每个顶点又拥有一个边列表。对于无向图而言，一条边会同时出现在边两边的两个顶点的邻接列表中。对于加权图而言，每条边还会存储一个值代表该边的权重。
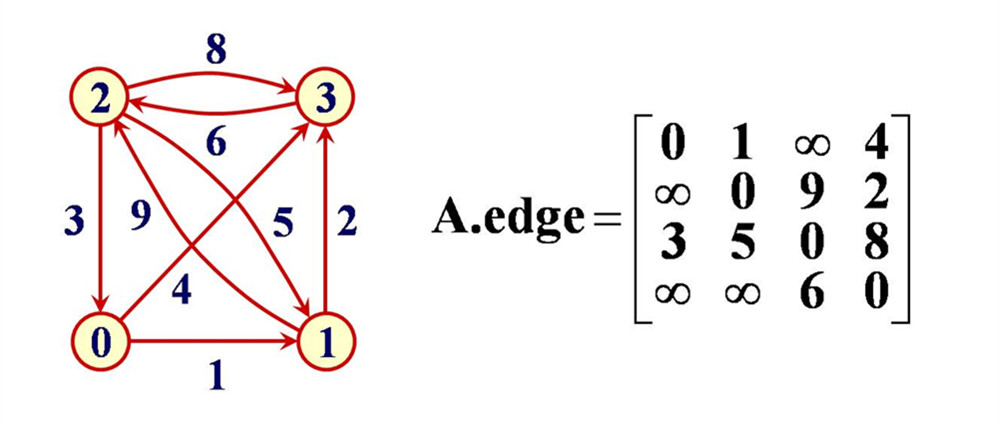
- 邻接矩阵是表示图形中顶点之间相邻关系的矩阵，对于n个顶点的图而言，该图的邻接矩阵有n行n列，每一个(行，列）或(列，行)代表了两个顶点之间的一条边。对于无向图，如果A1和A2之间有一条边，那么在二维矩阵中，matrix[A1,A2]和matrix[A2,A1]处的值为1。对于有向图，如果A1和A2之间有一条A1指向A2的边，那么matrix[A1,A2]处的值为1，matrix[A2,A1]处的值为0。对于加权图，把相应位置的1换成权值即可。
教材学习中的问题和解决过程
- 问题一：用邻接列表实现无向图的代码实现
- 问题一解决方案：邻接列表实现无向图相比用邻接矩阵实现我觉得其实要简单许多，主要体现在添加/删除边上，因为用邻接列表实现不需要通过循环来找到连接边的两个顶点的位置。
- 问题二：最先看到书上的邻接列表时比较懵逼，而且书上所述非常简单，不知道邻接列表的结构如何
- 问题二解决过程：先在网上查阅了部分资料后还是不太明白，仅仅是发现它的结构跟链地址法有些类似，但是如何实现的边不清楚，随后向王志强老师求助，王老师说的确跟链地址法比较类似，但是还有一个更加生动的例子就是糖葫芦串，每个顶点把与自己相接的顶点列在自己的后面就可以啦
代码调试过程中的问题和解决过程
-
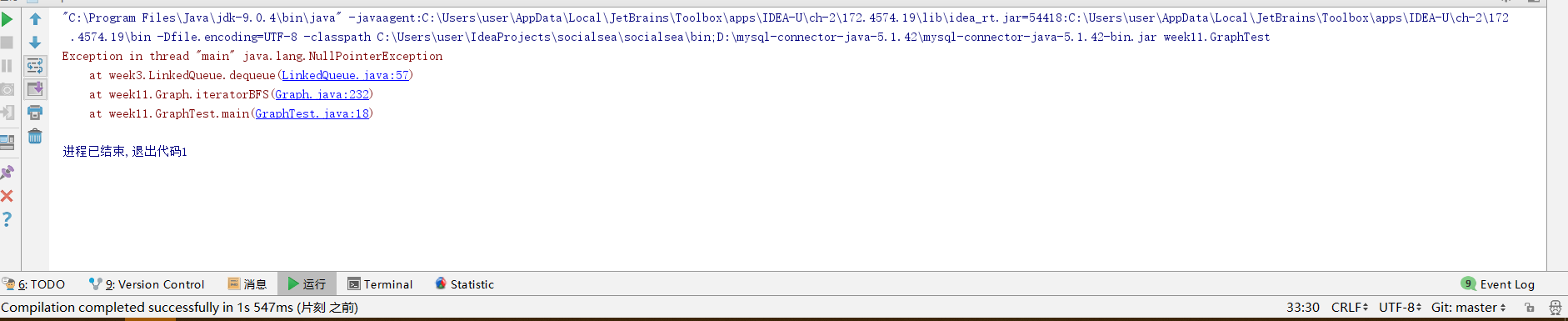
问题一：运行代码时出现下图错误：
-
问题一解决过程：是之前的链式队列的enqueue方法有问题，在else情况里增加一句
tail.setNext(node)就解决问题了
代码托管
上周考试课题总结
无考试
点评过的同学博客和代码
- 本周结对学习情况
20182306
学习进度条
| 代码行数（新增/累积） | 博客量（新增/累积） | 学习时间（新增/累积） | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 171/171 | 2/2 | 20/20 | |
| 第二三周 | 415/586 | 3/5 | 42/62 | |
| 第四周 | 587/1173 | 2/7 | 22/84 | |
| 第五周 | 1706/2879 | 2/9 | 19/103 | |
| 第六周 | 1706/2879 | 2/9 | 19/103 | |
| 第七周 | 3969/6848 | 2/11 | 21/124 | |
| 第八周 | 1217/8065 | 2/13 | 24/148 | |
| 第九周 | 2396/10461 | 2/15 | 22/170 | |
| 第十周 | 1826/12287 | 2/17 | 17/187 |
