最近公共祖先(LCA)详解
一、简介
对于有根树(不一定是二叉树) \(T\) 的两个结点 \(p、q\),最近公共祖先 \(LCA(T,p,q)\) 表示一个结点 \(x\),满足 \(x\) 是 \(p\) 和 \(q\) 的祖先且 \(x\) 的深度尽可能大。在这里,一个节点也可以是它自己的祖先。—— 百度百科
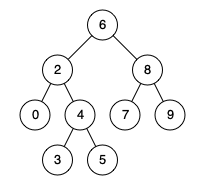
如图,节点 \(0\) 和 \(7\) 的 \(LCA\) 为 \(6\);节点 \(0\) 和 \(5\) 的 \(LCA\) 为 \(2\);节点 \(2\) 和 \(5\) 的 \(LCA\) 为 \(2\)。
二、解决方法
1、标记法(暴力)
解题思路
- 从根节点一直走到节点 \(p\),将路线上的节点进行记录为 \(path1\) 数组;
- 从根节点一直走到节点 \(q\),将路线上的节点进行记录 \(path2\) 数组;
- 同时遍历两个数组,返回最后一个相同的节点。
代码
class Solution {
public:
int lca(int root, int p, int q) {
vector<int> path1, path2, tmp;
function<void(int, int, int, int)> dfs = [&](int u, int fa, int p, int q) -> void {
tmp.push_back(u);
if (u == p) path1 = tmp;
if (u == q) path2 = tmp;
for (auto &v : adj[u]) {
if (v != fa)
dfs(v, u, p, q);
}
tmp.pop_back();
};
dfs(root, root, p, q);
int i = 0, n = min(path1.size(), path2.size());
while (i < n && path1[i] == path2[i]) i ++ ;
return path1[i - 1];
}
int lowestCommonAncestor(int root, int p, int q) {
return lca(root, p, q);
}
};
复杂度分析
时间复杂度:\(O(n)\);
空间复杂度:\(O(n)\)。
注意:当有 \(m\) 个询问时,需要对每对询问 \(dfs()\) 一次获取 \(path\) 数组,然后再遍历,时间复杂度为 \(O(mn)\)。
2、树上倍增法(朴素)
解题思路
- 选择 \(u\) 和 \(y\) 中深度较大的点,向上跳直到两者深度相同,然后两者同时向上跳直到两者第一次相遇,此时两者所在即是最近公共祖先。
- 使用 \(dfs\) 处理每个节点的深度;
- 模拟上述过程。
代码
class Solution {
private:
vector<int> fa(maxn, -1), depth(maxn, -1);
public:
int lca(int p, int q) {
if (depth[p] < depth[q]) swap(p, q);
while (depth[p] != depth[p]) p = fa[p]; // 同一深度
while (p != q) {
p = fa[p];
q = fa[q];
}
return p;
}
int lowestCommonAncestor(int root, int p, int q) {
function<void(int, int)> dfs = [&](int u, int father) -> void {
fa[u] = father; depth[u] = depth[father] + 1;
for (auto &v : adj[u]) {
if (v != father)
dfs(v, u);
}
};
dfs(root, root);
return lca(p, q);
}
};
复杂度分析
时间复杂度:\(O(n)\);
空间复杂度:\(O(n)\)。
注意:当有 \(m\) 个询问时,只需要 \(dfs()\) 一次获取每个节点的深度,然后再对每个询问找寻 \(LCA\),时间复杂度为 \(O(mn)\)。
3、树上倍增法(优化)
上述的朴素算法每次倍增为1,速度太慢。
- 按 \(2\) 的倍数来增大,也就是跳 $1, 2, 4, 8, 16, 32, …… $ 不过在这我们不是按从小到大跳,而是从大向小跳,即按 \(……, 32, 16, 8, 4, 2, 1\) 来跳,如果大的跳的超过了,再把它调小;
- 首先我们要记录各个点的深度和他们上 \(2^i\) 层的的祖先,用数组 \(depth\) 表示每个节点的深度,\(fa[i][j]\) 表示节点 \(i\) 的上 \(2^j\) 层祖先;
- 然后倍增 \(LCA\) 了,我们先把两个点提到同一高度,再统一开始跳;
- 但我们在跳的时候不能直接跳到它们的 \(LCA\),因为这可能会误判,所以我们要跳到它们 \(LCA\) 的下面一层。
// 预处理
void getdepth(int u,int father) {
depth[u] = depth[father]+1;
fa[u][0] = father;
for(int i = 1; (1 << i) <= depth[u]; i ++ )
fa[u][i] = fa[fa[u][i-1]][i-1]; // 这个转移可以说是算法的核心之一
// 意思是f的2^i祖先等于f的2^(i-1)祖先的2^(i-1)祖先
// 2^i=2^(i-1)+2^(i-1)
for(auto &v : adj[u]) {
if(v != father)
getdepth(v, u);
}
}
depth[root] = -1;
getdepth(root, root);
log2n = log(n) / log(2) + 0.5;
int lca(int u,int v) {
int depu = depth[u], depv = depth[v];
if(depu != depv) { //先跳到同一深度
if(depth[u] < depth[v]) {
swap(u,v);
swap(depu,depv);
}
int d = depu - depv;
for(int i = 0; i <= log2n; i ++ )
if((1 << i) & d)
u = fa[u][i];
}
if(u == v) return u;
for(int i = log2n; i >= 0; i -- ) {
if(depth[fa[u][i]] <= 0) continue;
if(fa[u][i] == fa[v][i]) continue;
else u = fa[u][i], v = fa[v][i]; // 因为我们要跳到它们LCA的下面一层,所以它们肯定不相等,如果不相等就跳过去。
}
return fa[u][0];
}
复杂度分析
时间复杂度:预处理:\(O(nlogn)\),每次 \(lca\) :\(O(logn)\);
空间复杂度:\(O(n)\)。
注意:当有 \(m\) 个询问时,只需要 \(getdepth()\) 一次预处理,然后再对每个询问找寻 \(LCA\),时间复杂度为 \(O(mlogn)\)。
4、Tarjan(离线)算法
待续...



 浙公网安备 33010602011771号
浙公网安备 33010602011771号