Games101___Transformation变换
Transformation
2D Transformation
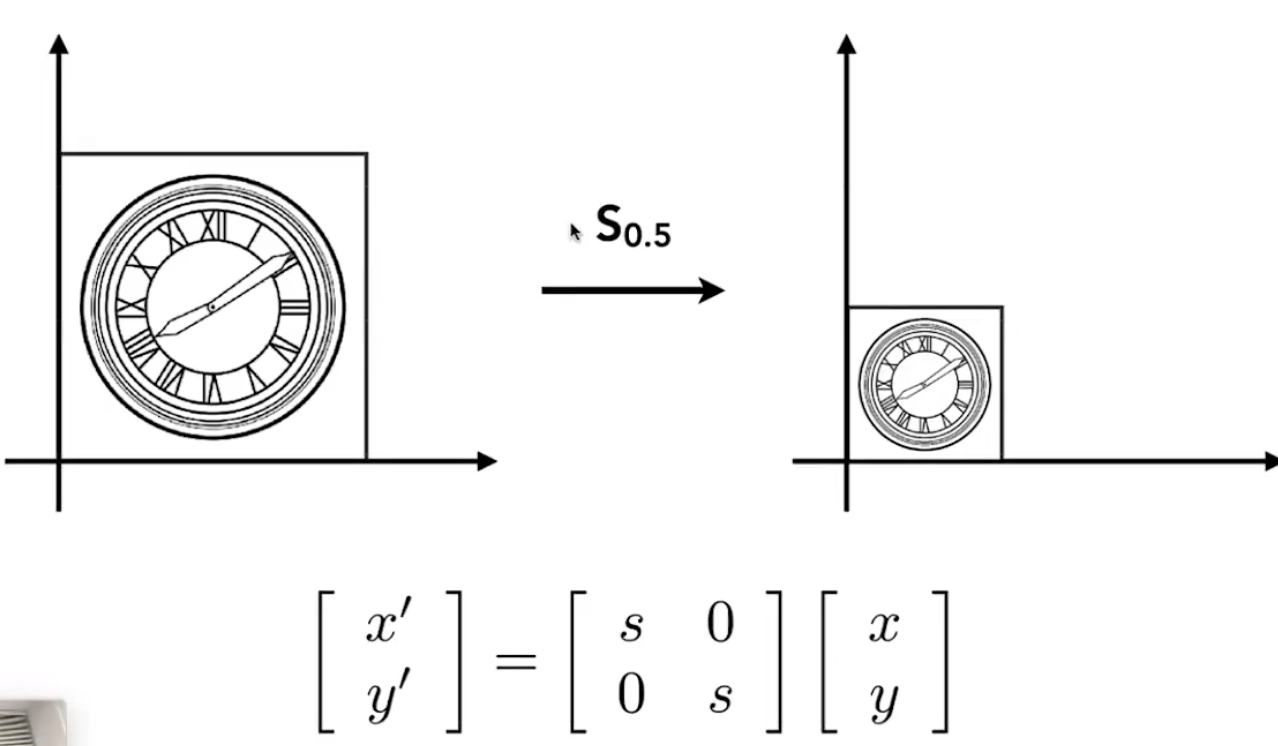
Scale
Scale Matrix
缩放矩阵
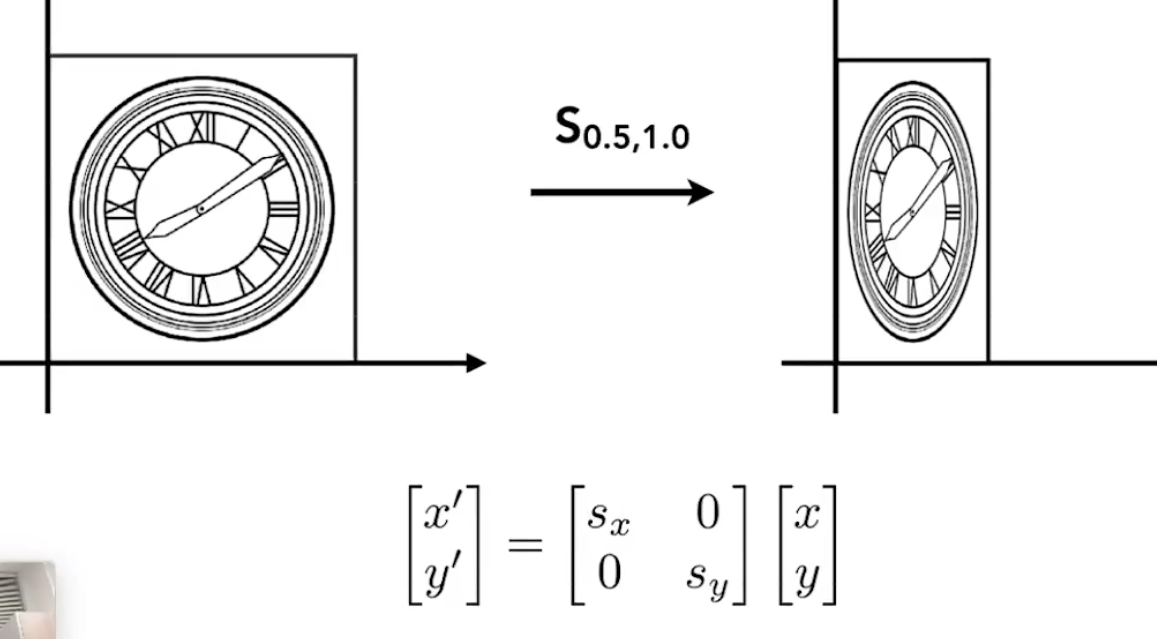
非均匀缩放
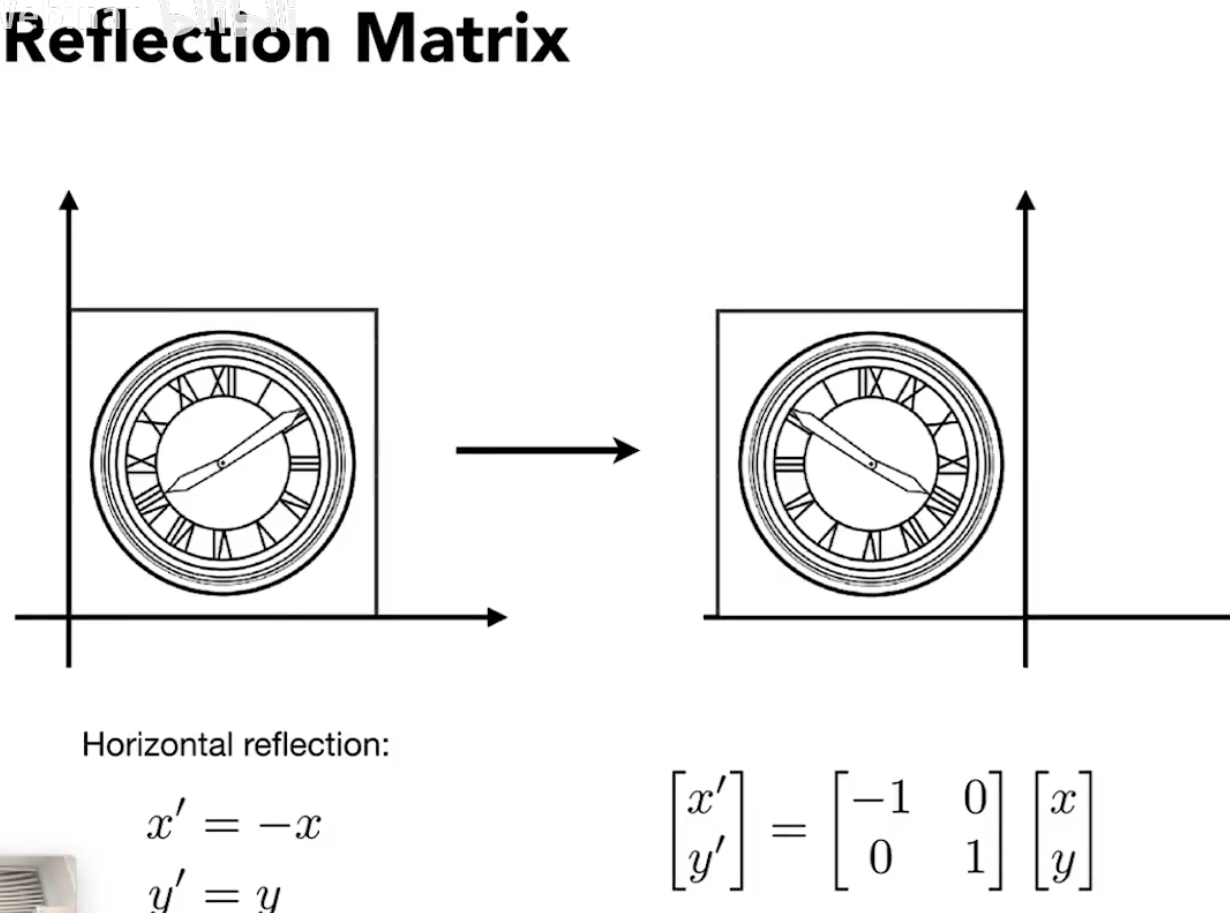
Reflection Matrix 反转
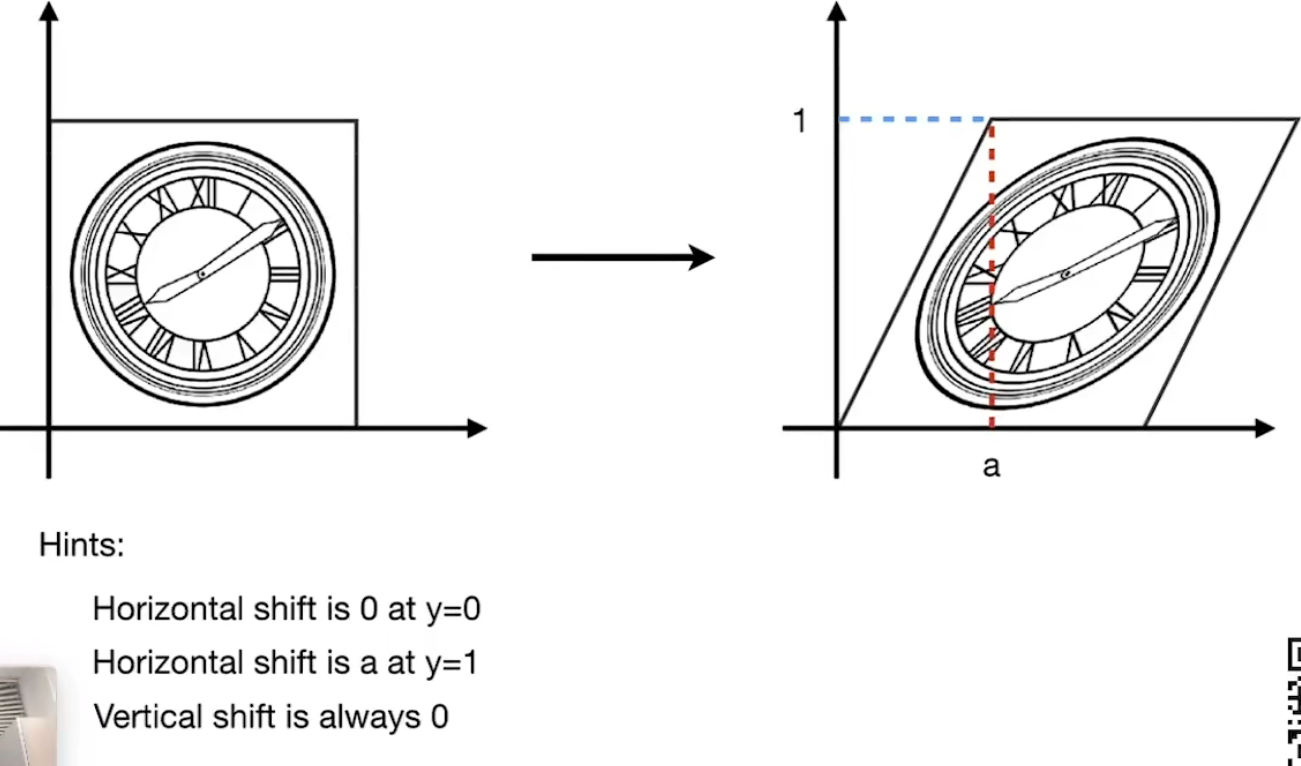
Shear Matrix 切变
horizontal shift 水平位移
Vertical shift 垂直位移
水平方向移动都是 a*y
比如:原先是(0,1)=> (a,1) , (0,0.5) => (0.5*a,0.5)
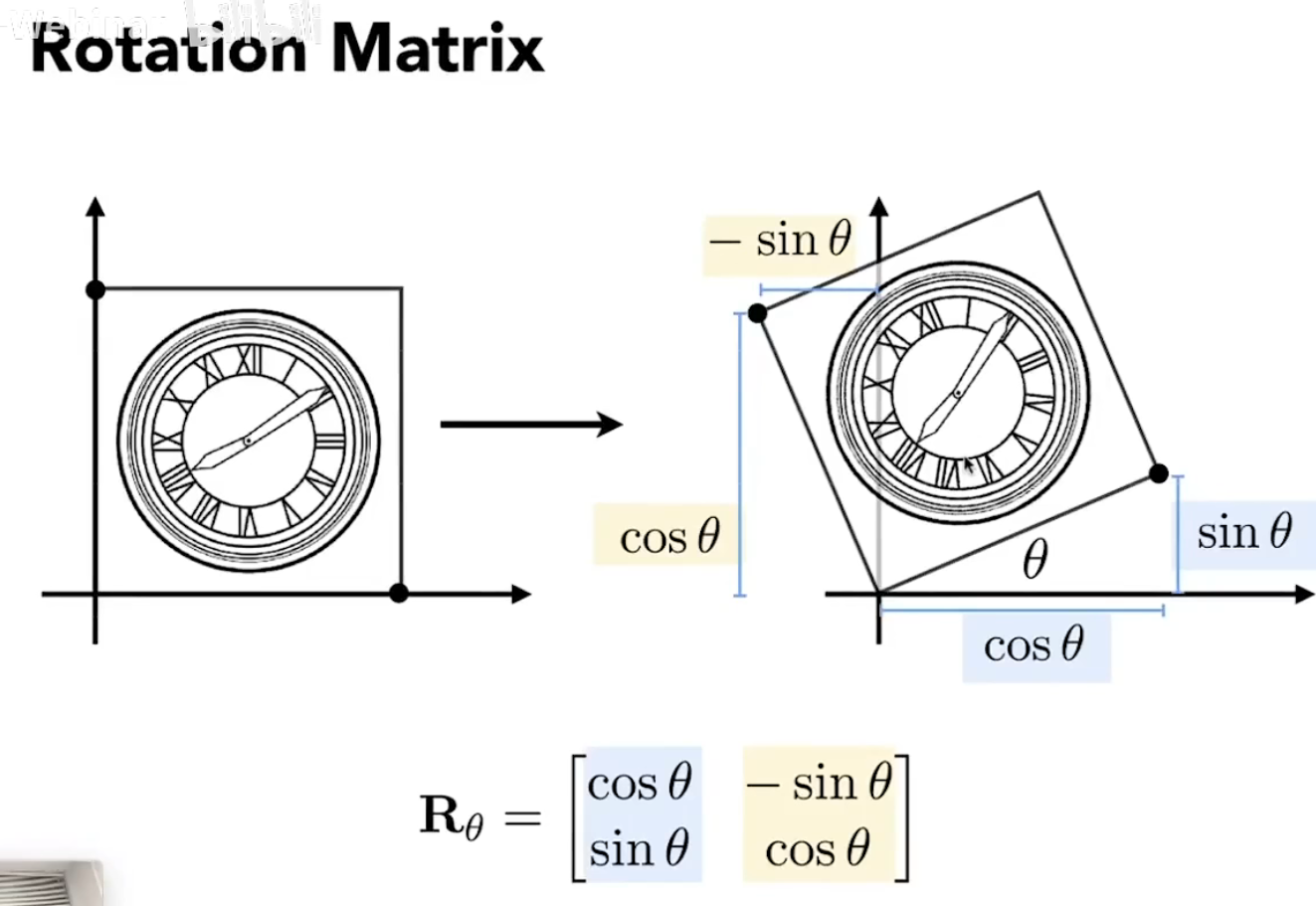
Rotate(about the origin(0,0),CCW by default)
没说方向就是逆时针,默认原点旋转
简单的证明方法:
可以带入两个点(0,1),(1,0),以及对应变化后的两个点 \((cos(θ),sin(θ)) ,(-sin(θ),cos(θ))\)
带入矩阵计算即可得到
Same dimension
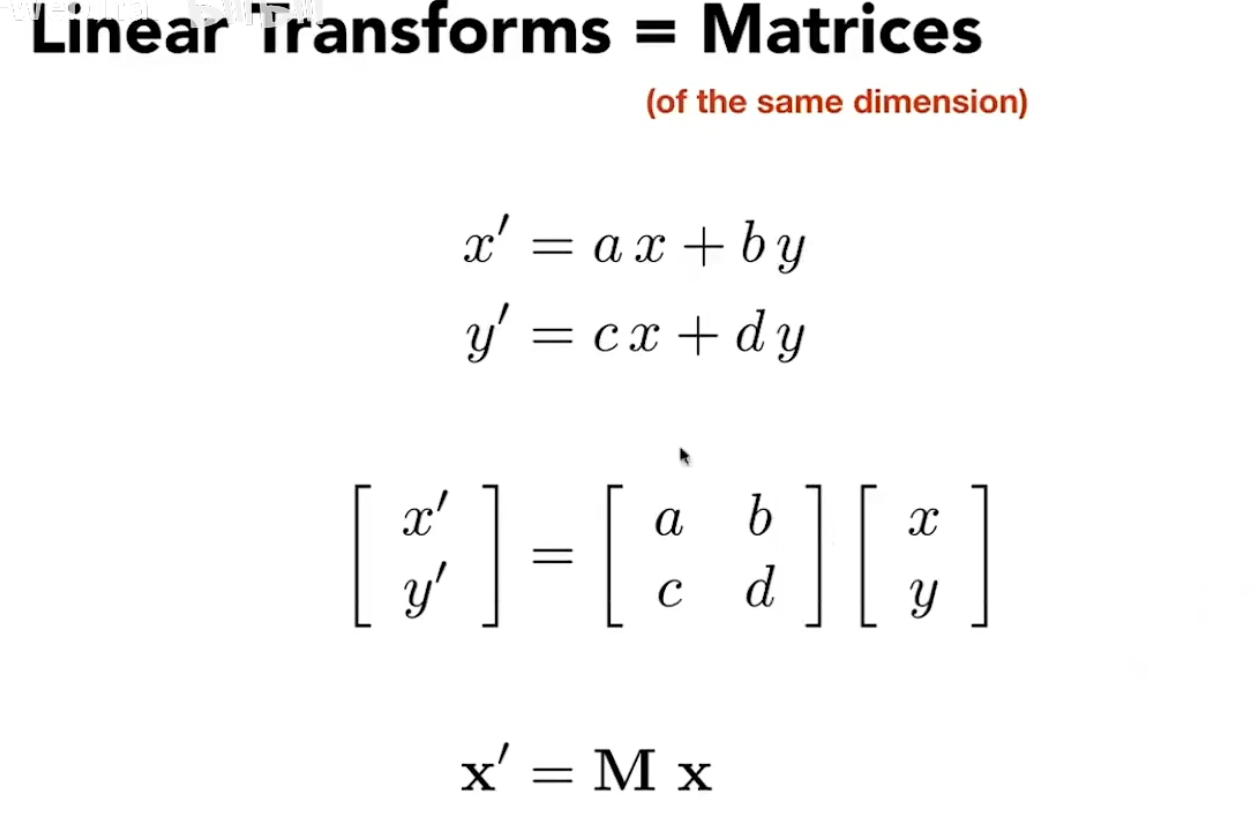
Homogeneous coordinates 齐次坐标
Translation 平移
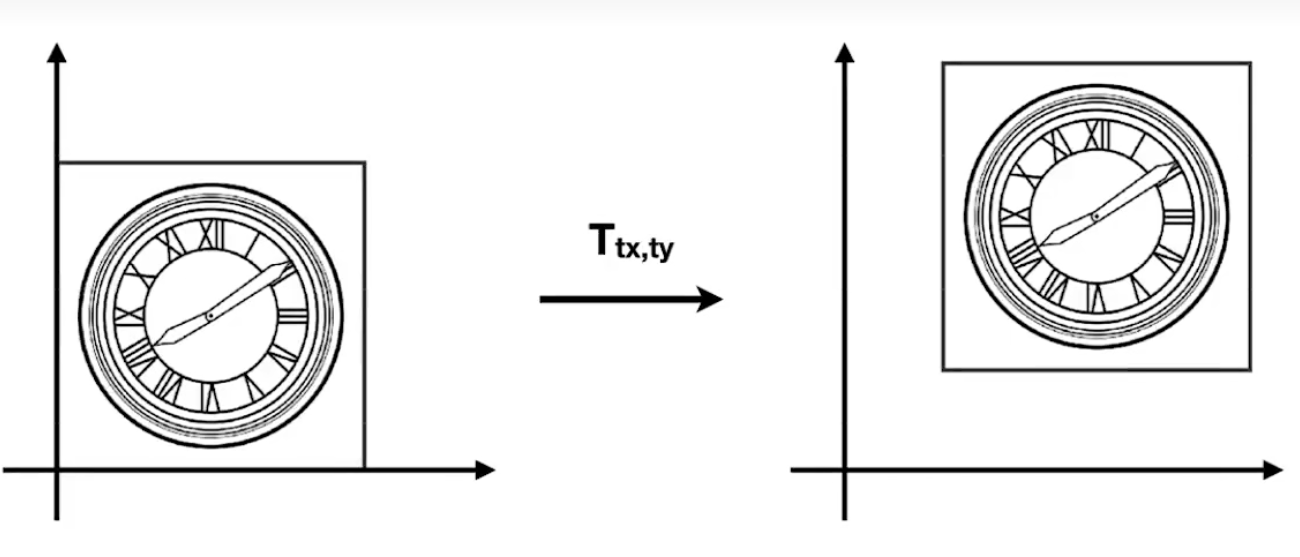
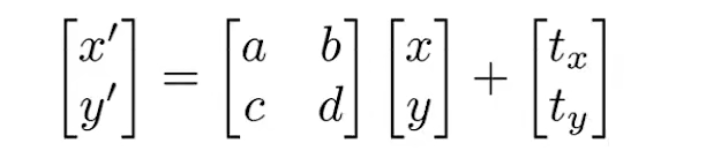
trade off 权衡
solution: Homogenous Coordinates

弊端:原点坐标不为(0,0,0)

两个point 相加为 中点

Affine Transformations 仿射变换
所有仿射变换都可以用齐次坐标表示
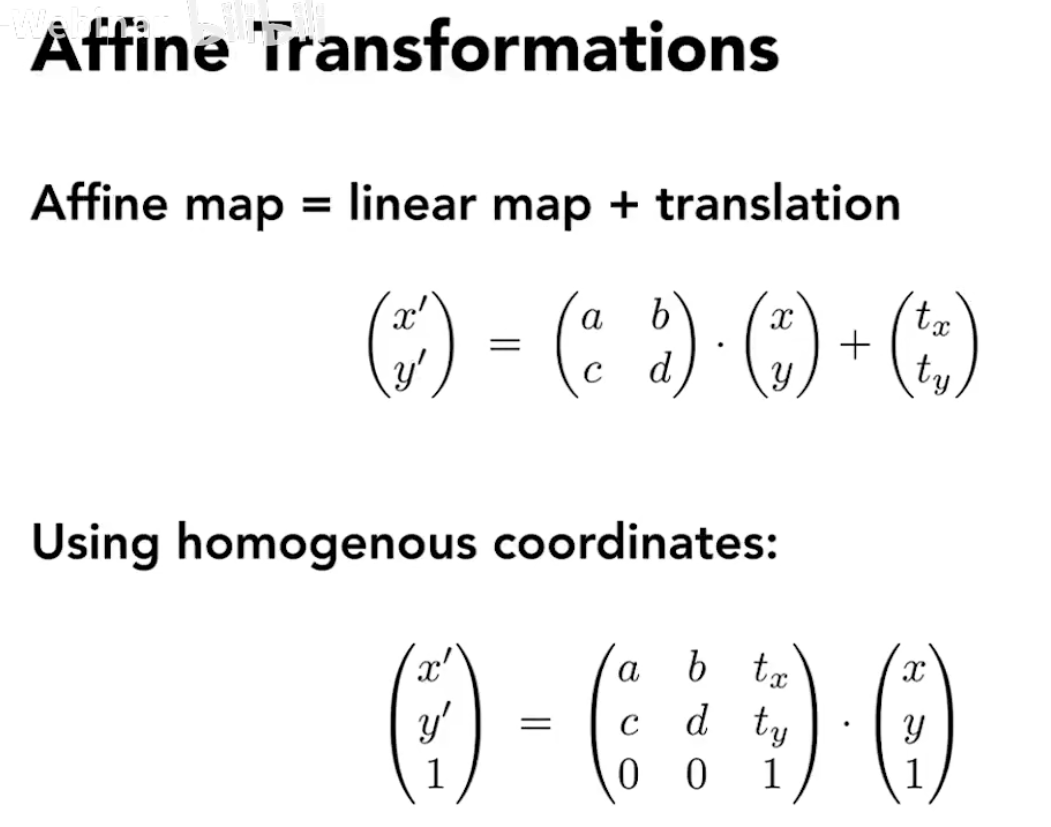

Inverse Transform 逆变换
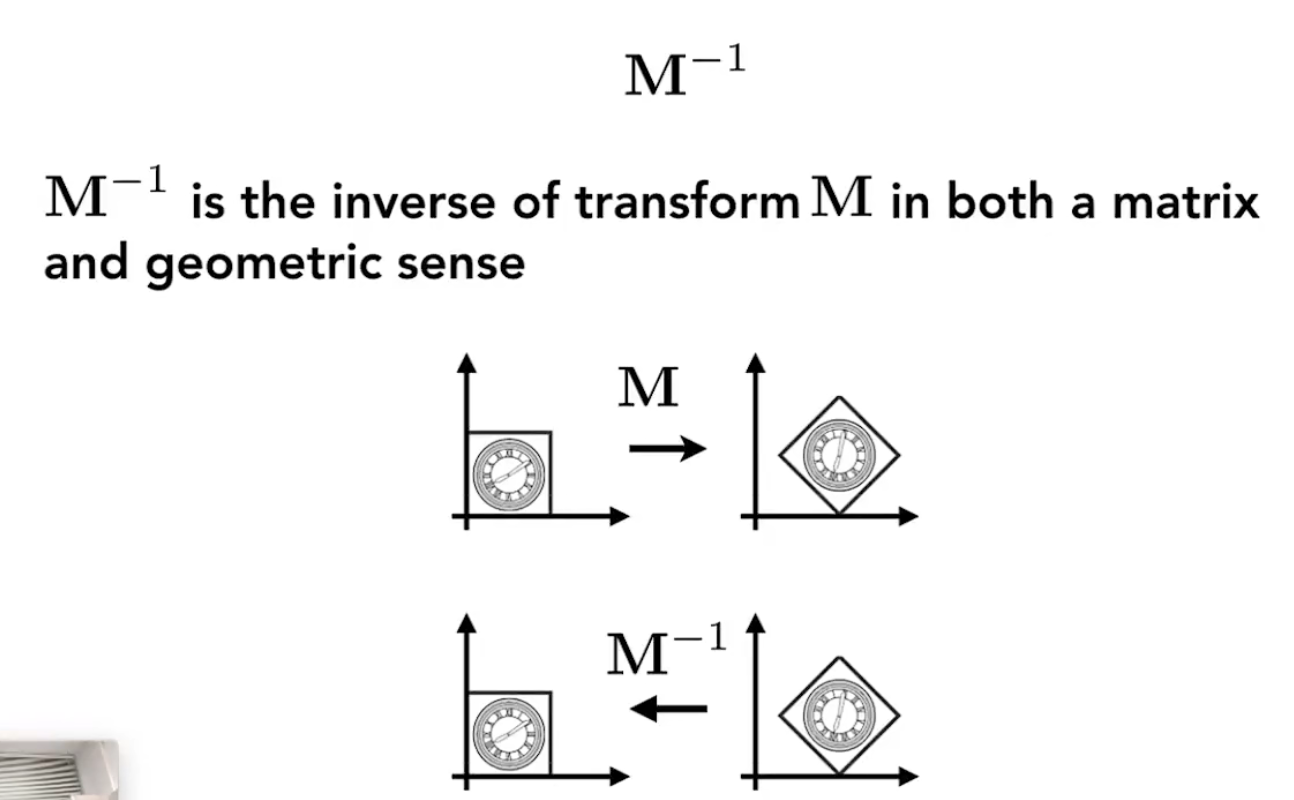
矩阵变换不满足交换律
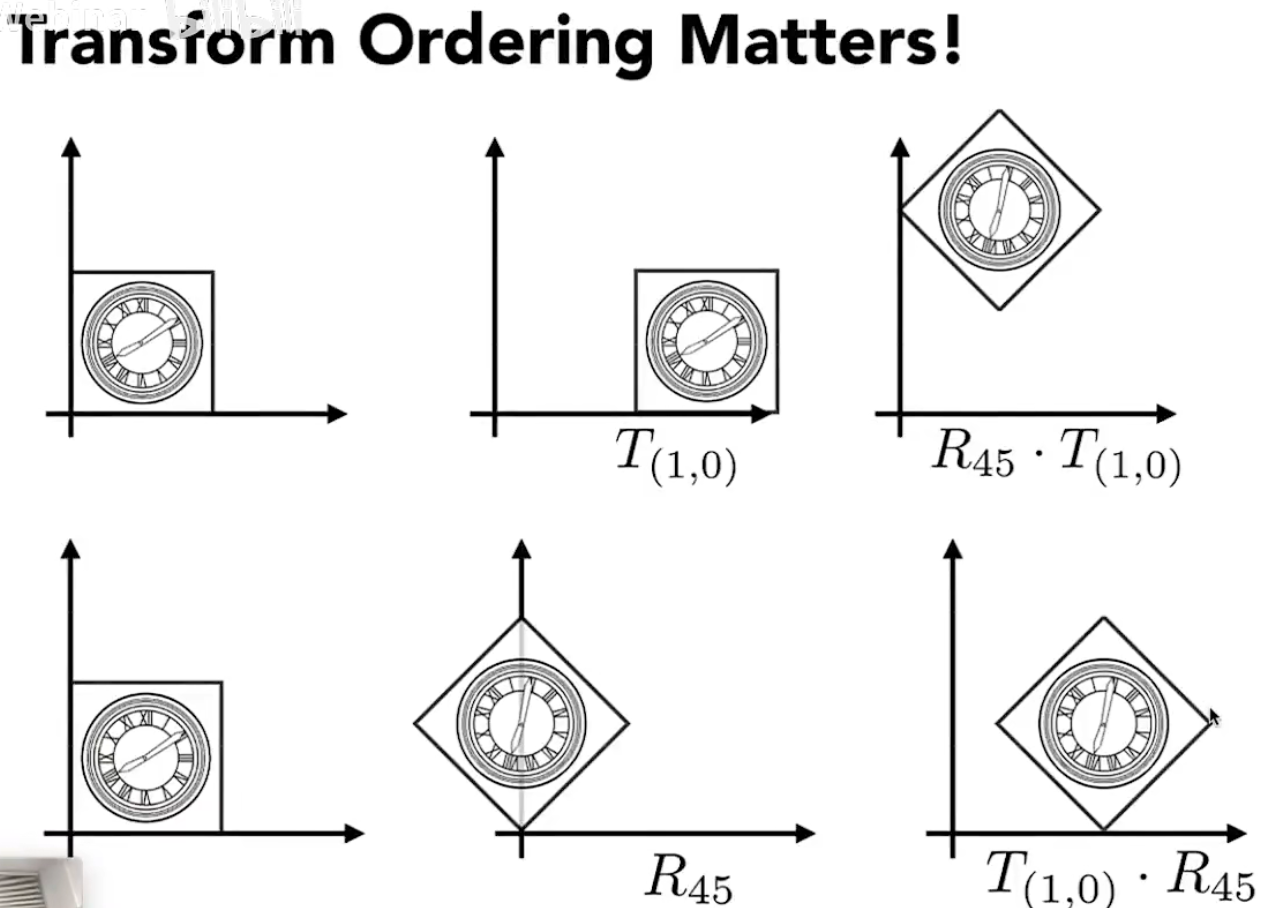

从右到左,先旋转再平移
但是矩阵有交换律,可以把复杂的变换组合起来
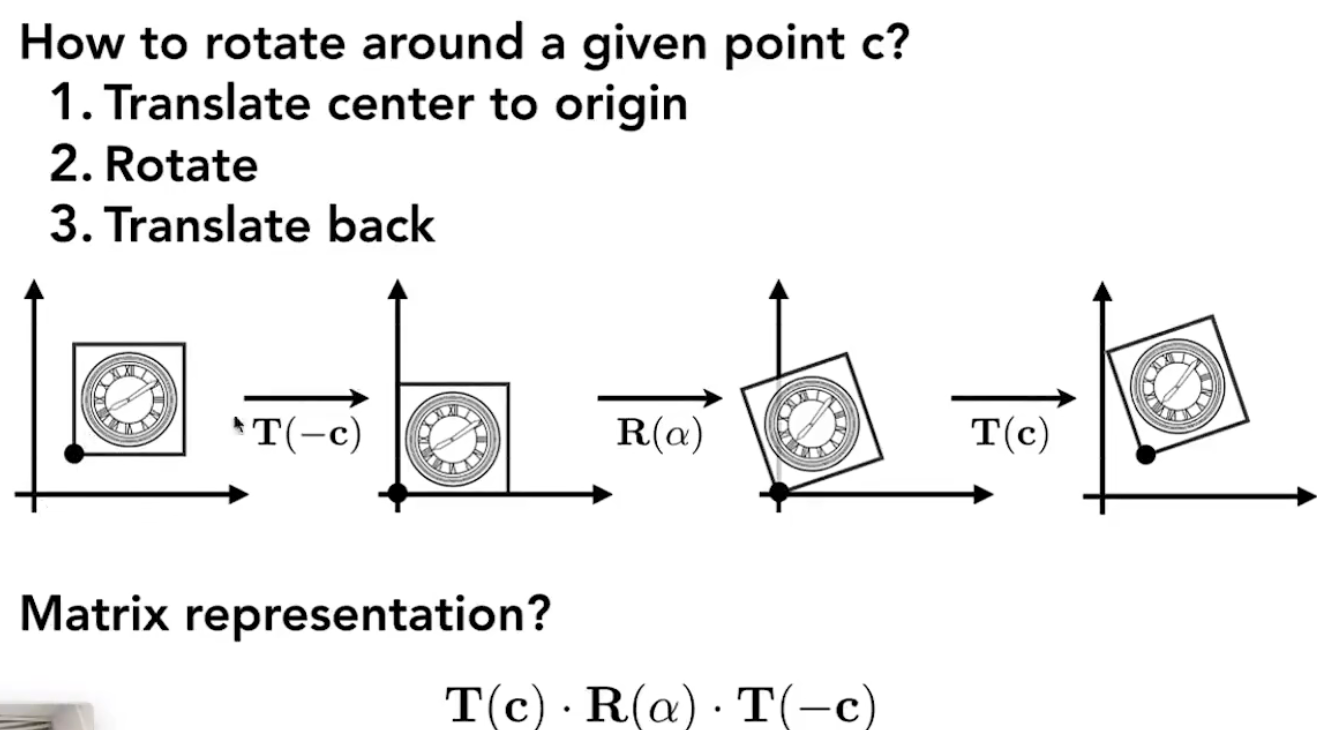
分解复杂的变换
3D Transforms
类似2D的齐次坐标

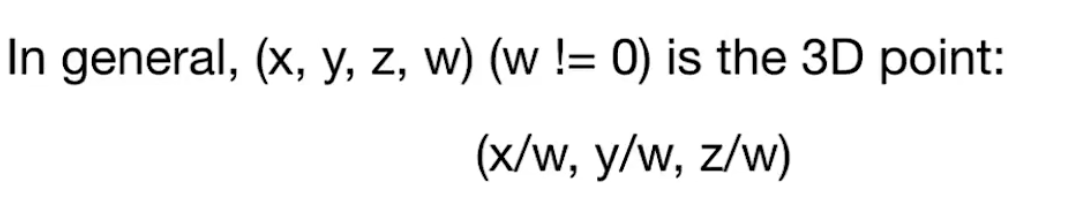
先线性变换再平移
homework
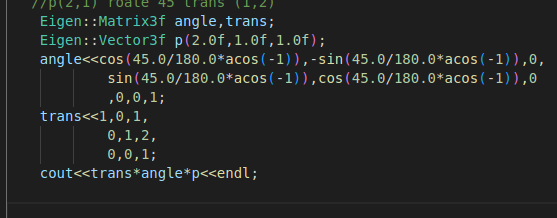
给定一个点 P=(2,1), 将该点绕原点先逆时针旋转 45◦,再平移 (1,2), 计算出
变换后点的坐标(要求用齐次坐标进行计算)。

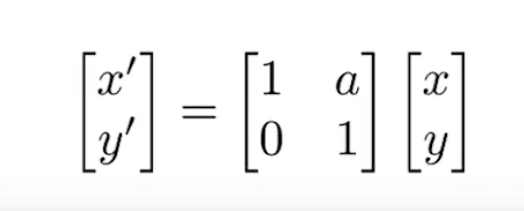

 浙公网安备 33010602011771号
浙公网安备 33010602011771号