96. 不同的二叉搜索树(leetcode)

https://leetcode.cn/problems/unique-binary-search-trees/solutions/329807/bu-tong-de-er-cha-sou-suo-shu-by-leetcode-solution/

较为困难的一道DP题,需要分析各个情况,以及想到如下思路:

给定一个有序序列 1⋯n，为了构建出一棵二叉搜索树，我们可以遍历每个数字 i，将该数字作为树根，将 1⋯(i−1) 序列作为左子树，将 (i+1)⋯n 序列作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。

需要想到以不同的数作为根节点得到的二叉搜索树,其递推方程为左子树种数*右子树种数这个难点,最后把不同的数作为根节点得到的结果求和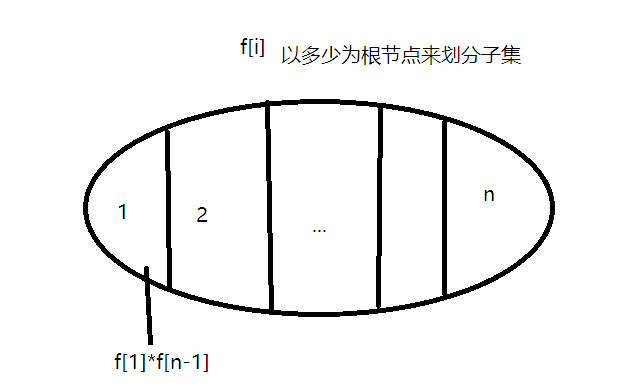

class Solution {
    public int numTrees(int n) {
        // dp[i]表示到1~i组成的节点有多少种不同的二叉搜索树
        // dp[i] = dp[1~j-1] * dp[j~i];
        int[] dp = new int[n+1];
        dp[0]=1; // 为空也是一种二叉树
        for (int i = 1; i <= n; i++) {
            // 以多少为根节点来划分左右子树,划分子集
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j]; // 左子树种数*右子树种数,即1~(j-1) 和 j~(i-j)
            }
        }
        return dp[n];       

    }
}