线段树模板

如图所示,线段树维护的是一个struct,一个区间和,对于一个序列,他会不断地分开序列,并且在每个结点存在当前结点的区间和,直到分为1个数
对于如何奇偶分段,使用mid=R+L >> 1再下取整

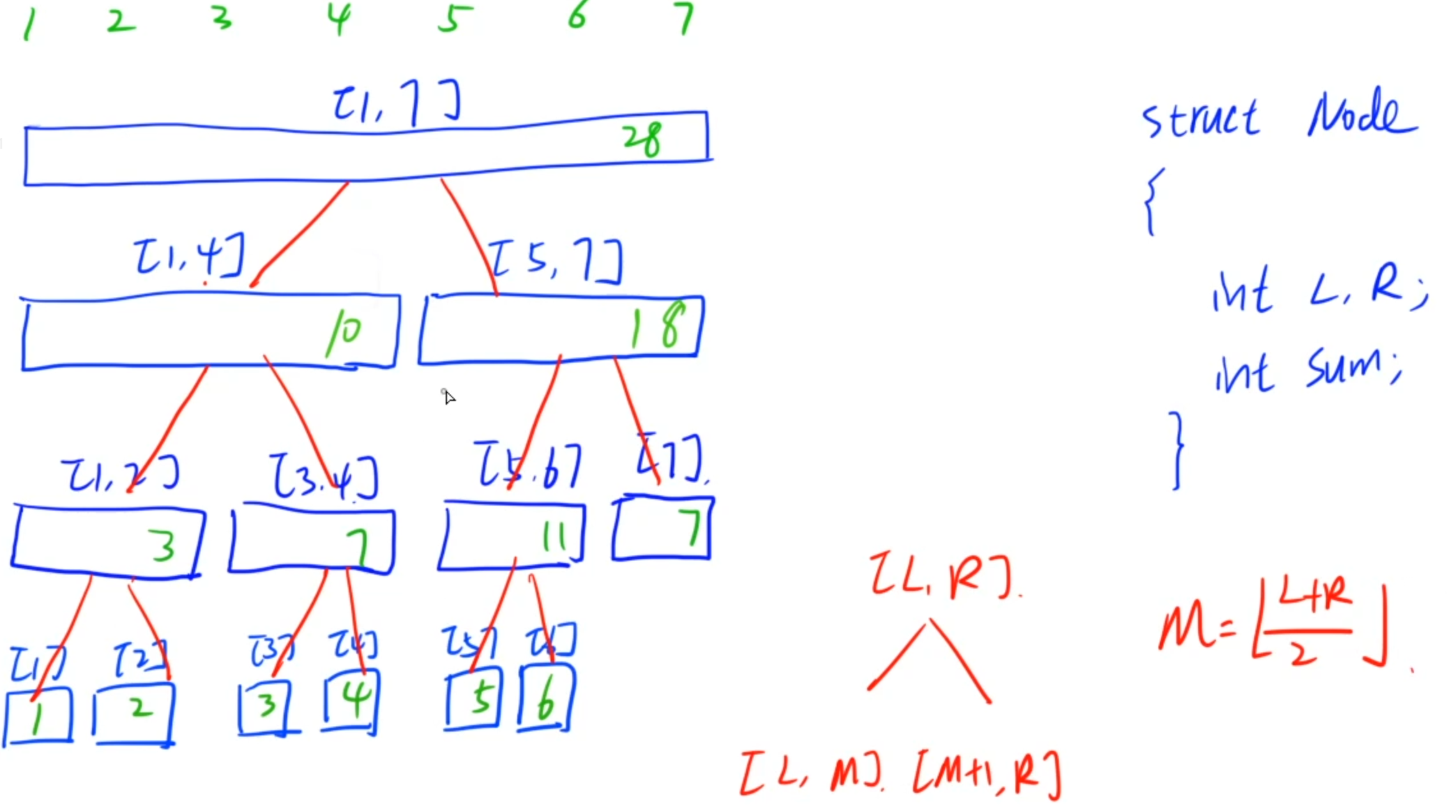
而它的操作和树状数组有点类似:支持单点修改(即只改信息需要变化的结点)

如图,假设将原序列中的5改为8,则实际上需要修改的结点只有包含5的,即原来的[5,7],[5,6],[5]

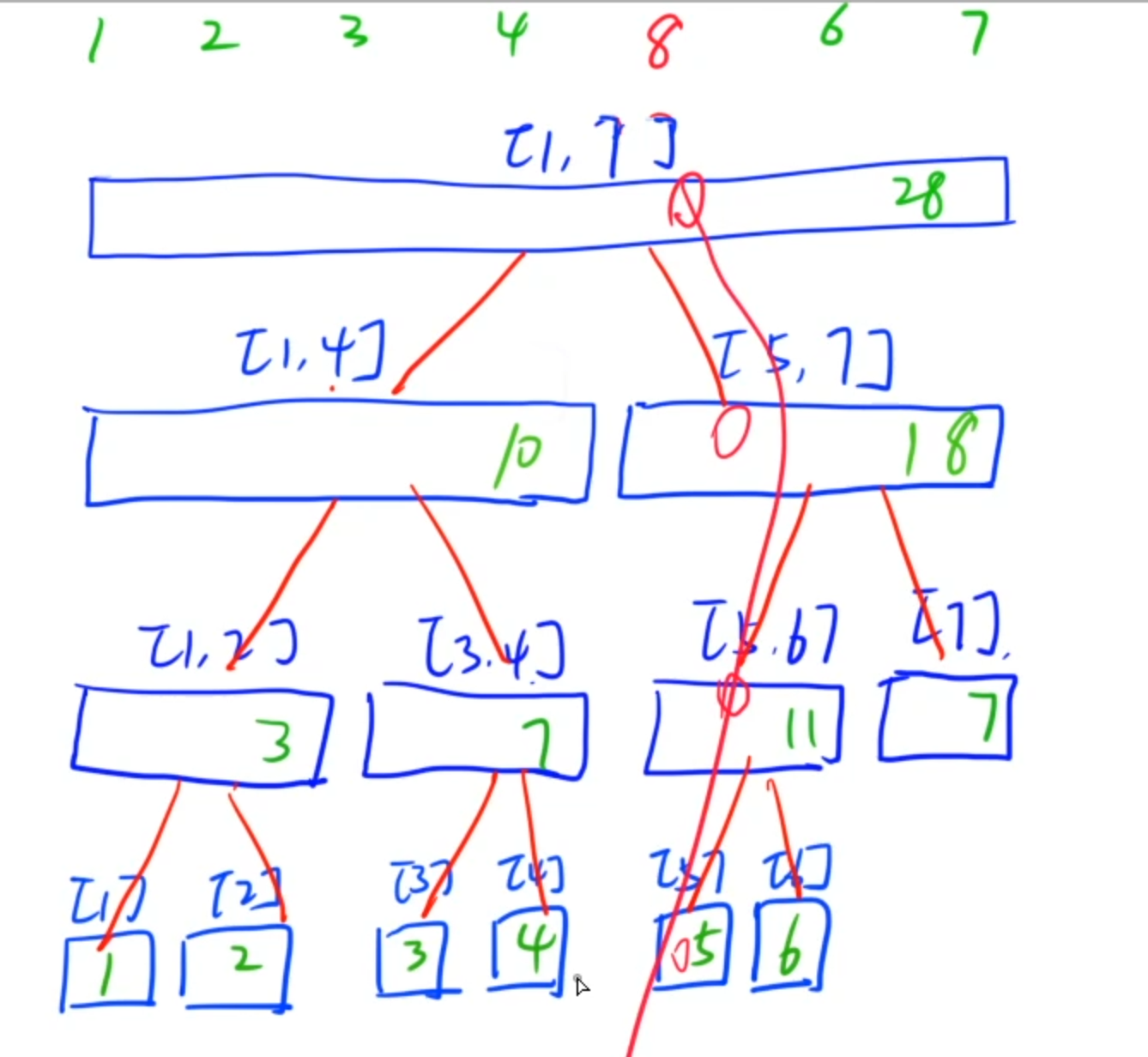
然后就需要更新结点,利用递归的方式,先递归到叶子结点,将叶子结点的[5],更改为[8],然后回溯父结点,根据已经修改过的子节点[8]与子节点[6]的和来修改其本身的值11->14,其后也是相同,即修改为两个儿子之和
显然这样的操作的时间复杂度是logn,

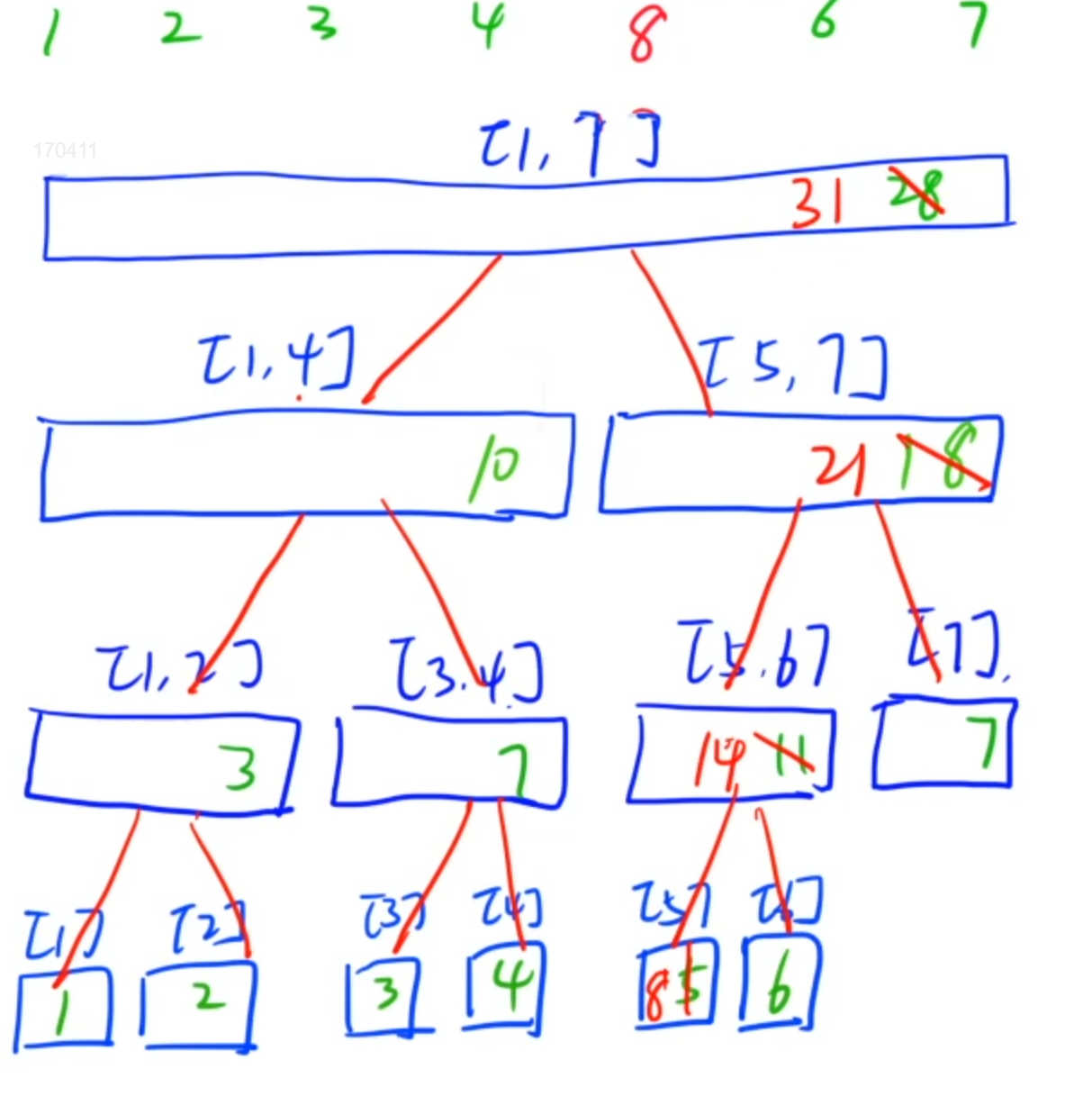
它的第二个操作是:区间查询(即询问某个区间的)时间:(logn)
它所使用的的也是递归,首先查看当前区间是否满足完全在所求区间内部,即当前区间被包含于所求区间
若不完全包含,则继续向下递归,如此相同操作,直到找到区间完全满足包含于所求区间中,就不必再递归了
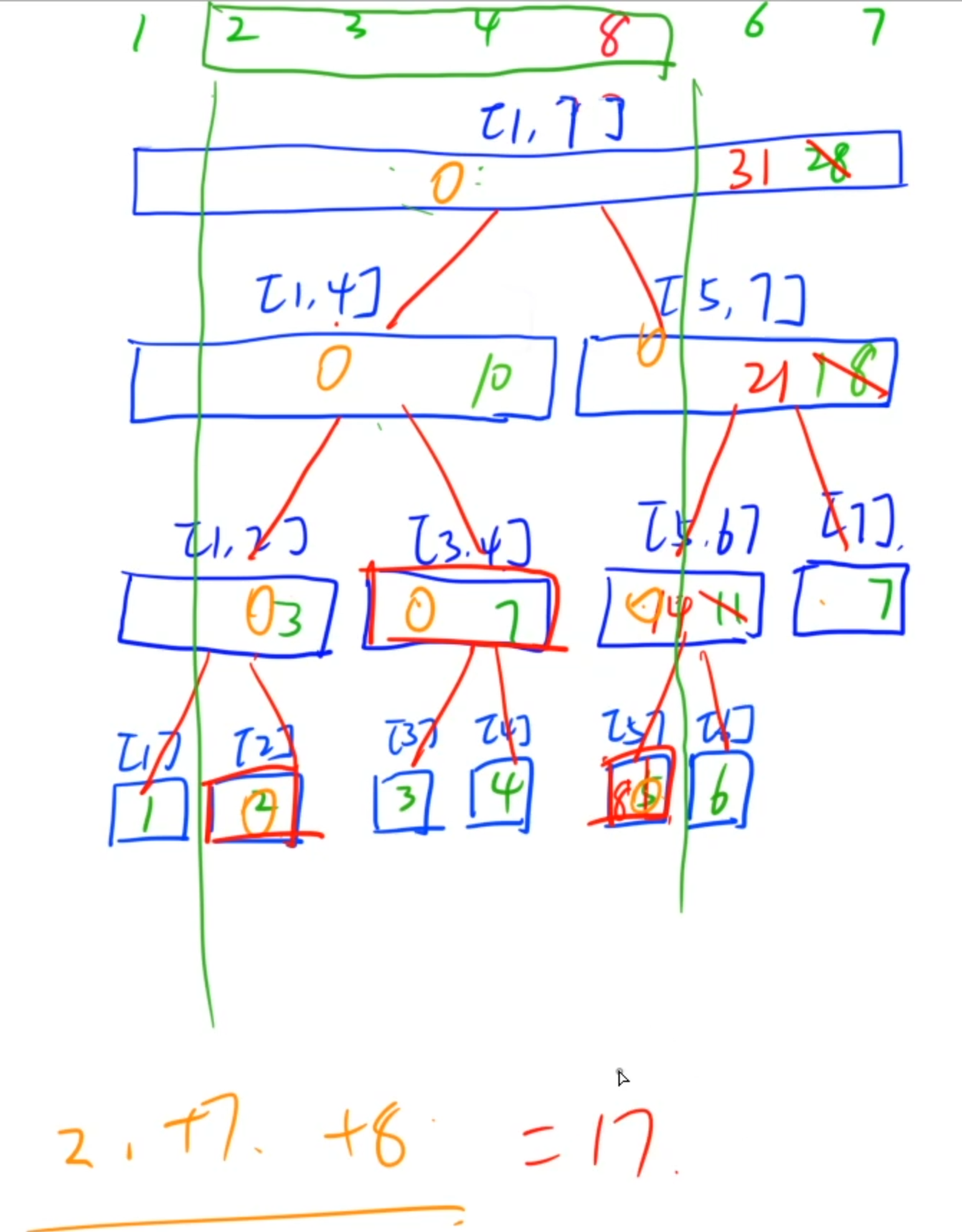
如图所示,若求[2,5]这段区间的和,先判断当前总区间是否满足包含于所求区间,显然[1,7]明显不包含与[2,5]中,则继续向下递归
分为[1,4]与[5,7],显然也都不满足包含于[2,5]中,则继续递归
分为[1,2],[3,4]与[5,6],[7],这四段中显然只有[3,4]满足包含于[2,5]中,因此[3,4]不必再递归了,直接使用[3,4]的区间和即可,而其他的需要继续递归
分为[1],[2]与[5],[6],明显只有[2],[5]满足要求,则使用他们的区间和,或者说本身值即可
如此,所求区间被分为了区间[2]+[3,4]+[5]的和,即17

四个操作:

存储方式最大开4n

https://www.acwing.com/problem/content/1266/

这里太长了,直接转载别人的了..

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;

const int N=100010;

int n,m;

int w[N];//记录一下权重

struct node{
    int l,r;//左右区间

    int sum;//总和
}tr[N*4];//记得开 4 倍空间

void push_up(int u)//利用它的两个儿子来算一下它的当前节点信息
{
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;//左儿子 u<<1 ,右儿子 u<<1|1  
}

void build(int u,int l,int r)/*第一个参数，当前节点编号，第二个参数，左边界，第三个参数，右边界*/
{
    if(l==r)tr[u]={l,r,w[r]};//如果当前已经是叶节点了，那我们就直接赋值就可以了
    else//否则的话，说明当前区间长度至少是 2 对吧，那么我们需要把当前区间分为左右两个区间，那先要找边界点
    {
        tr[u]={l,r};//这里记得赋值一下左右边界的初值

        int mid=l+r>>1;//边界的话直接去计算一下 l + r 的下取整

        build(u<<1,l,mid);//先递归一下左儿子

        build(u<<1|1,mid+1,r);//然后递归一下右儿子

        push_up(u);//做完两个儿子之后的话呢 push_up 一遍u 啊，更新一下当前节点信息
    }
}

int query(int u,int l,int r)//查询的过程是从根结点开始往下找对应的一个区间
{
    if(l<=tr[u].l&&tr[u].r<=r)return tr[u].sum;//如果当前区间已经完全被包含了，那么我们直接返回它的值就可以了
    //否则的话我们需要去递归来算
    int mid=tr[u].l+tr[u].r>>1;//计算一下我们 当前 区间的中点是多少
    //先判断一下和左边有没有交集

    int sum=0;//用 sum 来表示一下我们的总和

    if(mid>=l)sum+=query(u<<1,l,r);//看一下我们当前区间的中点和左边有没有交集
    if(r>=mid+1)//看一下我们当前区间的中点和右边有没有交集
    sum+=query(u<<1|1,l,r);

    return sum;

}

void modify(int u,int x,int v)//第一个参数也就是当前节点的编号,第二个参数是要修改的位置，第三个参数是要修改的值
{
    if(tr[u].l==tr[u].r)tr[u].sum+=v; //如果当前已经是叶节点了，那我们就直接让他的总和加上 v 就可以了

    //否则
    else
    {

      int mid=tr[u].l+tr[u].r>>1;
      //看一下 x 是在左半边还是在右半边
      if(x<=mid)modify(u<<1,x,v);//如果是在左半边，那就找左儿子
      else modify(u<<1|1,x,v);//如果在右半边，那就找右儿子

      //更新完之后当前节点的信息就要发生变化对吧，那么我们就需要 pushup 一遍

      push_up(u);
    }

}

int main()
{
    scanf("%d%d",&n,&m);

    for(int i=1;i<=n;i++)scanf("%d",&w[i]);

    build(1,1,n);/*第一个参数是根节点的下标，根节点是一号点，然后初始区间是 1 到 n */

    //后面的话就是一些修改操作了

    while(m--)
    {
        int k,a,b;

        scanf("%d%d%d",&k,&a,&b);

        if(!k)printf("%d\n",query(1,a,b));//求和的时候，也是传三个参数，第一个的话是根节点的编号 ，第二个的话是我们查询的区间 
        //第一个参数也就是当前节点的编号
        else
        modify(1,a,b);//第一个参数是根节点的下标,第二个参数是要修改的位置，第三个参数是要修改的值

    }


    return 0;
}

作者：Elegant
链接：https://www.acwing.com/solution/content/40394/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。