788. 逆序对的数量
https://www.acwing.com/problem/content/description/790/
y总的思路
我的理解
究其分治,底层原理,大概是:
利用归并排序的分治特点,一次分两组
最终分成单位为1,即只有1个数的组
即第1,第2中情况都被分成了第三种情况
由于只有1个数.即每个序列都有序,可以很轻松算出是否为逆序对,回溯求和即可
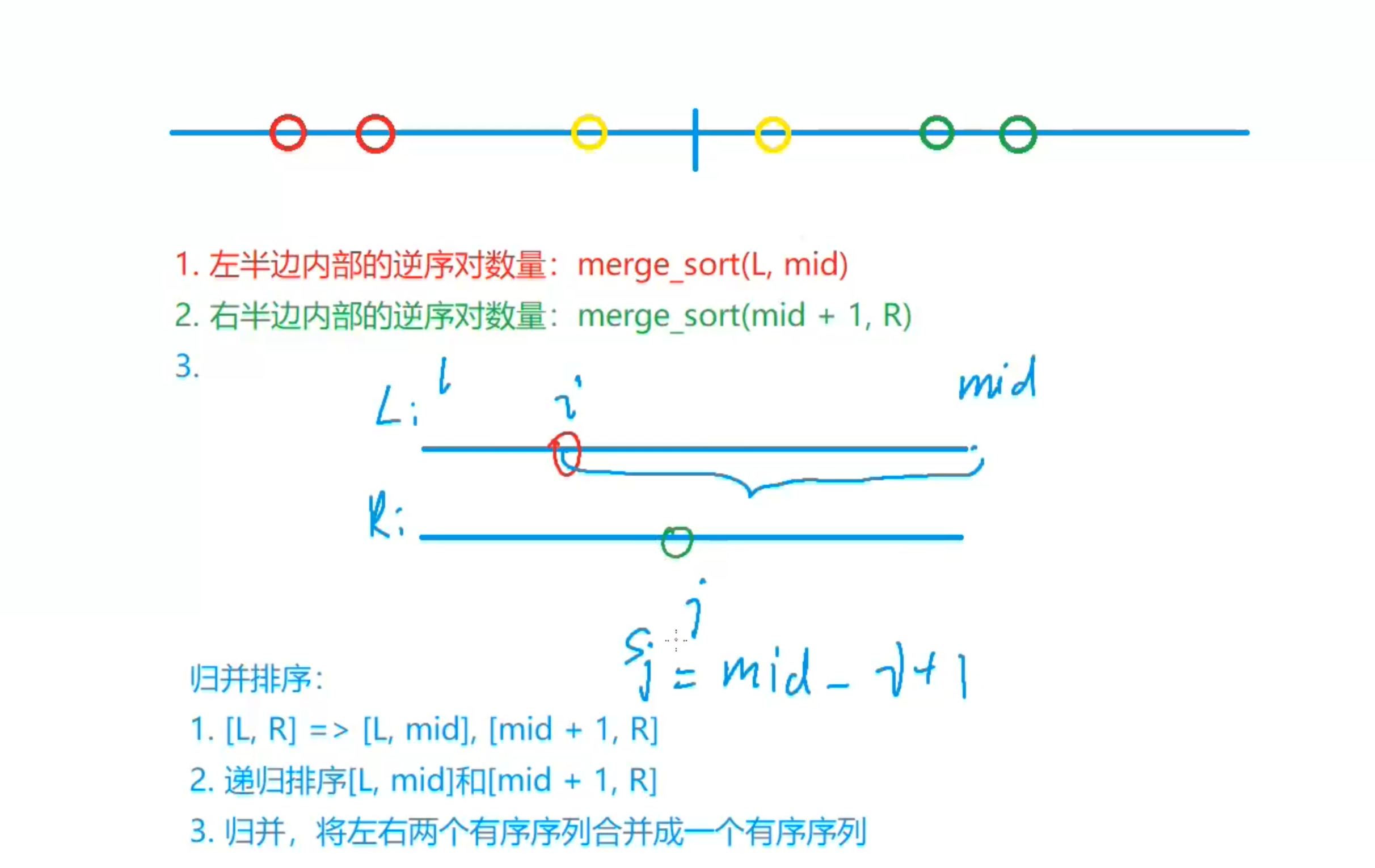
从高处看:
对于任意两个组L,R,,相对于R组j元素来说,它在L组中逆序对的数量为mid-i+1
即可知一组的逆序对数量,求和所有组的逆序对数量即可
或者可以看看这篇题解:https://www.acwing.com/solution/content/17978/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
typedef long long LL;
int n;
int q[N],tmp[N];
LL merge_sort(int l,int r)
{
if(l >= r) return 0;
LL mid=l+r >> 1;
LL res = merge_sort(l,mid) + merge_sort(mid+1,r);
int k=0,i=l,j=mid+1;
while(i <= mid && j <= r)
if(q[i] <= q[j]) tmp[k++]=q[i++];
else
{
tmp[k++]=q[j++];
res+=mid-i+1;
}
while(i <= mid) tmp[k++]=q[i++];
while(j <= r)tmp[k++]=q[j++];
for(int i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];
return res;
}
int main()
{
cin >> n;
for(int i=0;i<n;i++)cin >> q[i];
cout << merge_sort(0,n-1) << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号