浅谈递归入门（1） - 指南

声明

由于个人技术原因，难免有讲错、不专业的地方，欢迎大家指正！

简介

递归（recursive algorithm）是指一种通过重复将问题分解为同类的子问题而解决问题的方法。并且可以完全替代循环。递归就是在过程或函数里调用自身的算法。

案例1

题目描述

编程求 

结果不超过 long long 范围

输入格式

输入一行，只有一个整数  

输出格式

输出只有一行（这意味着末尾有一个回车符号），包括 1 个整数。

输入输出样例

样例 1

输入样例

5

输出样例

120

样例 2

输入样例 

10

输出样例 

3628800

本例中，有如下思路：

那么该如何实现呢？请看下方代码：

#include 
using namespace std;
long long n;//数据
long long fun(long long x){//递归函数
    if(x==1)return 1;//终止条件
    else return x*fun(x-1);//调用自身
}
int main(){
    cin>>n;
    cout<

注意第5行代码，它的作用是作为递归的终止条件，因为如果无终止条件，那么递归就会陷入死循环出bug。

第6行代码就是递归函数在调用自身，以计算阶乘，就是把上文公式重复调用。

案例2

题目描述

菲波那契数列是指这样的数列: 数列的第一个和第二个数都为 1，接下来每个数都等于前面 2 个数之和。

给出一个正整数 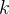 ，要求菲波那契数列中第  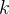个数是多少。

输入格式

输入一行，包含一个正整数 。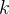

输出格式

输出一行，包含一个正整数，表示菲波那契数列中第 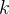 个数的大小

输入输出样例

样例 1

输入样例 复制

4

输出样例 复制

3

在本例中提到了斐波那契数列，递推公式为：

因此，易得出下文代码：

#include 
using namespace std;
long long mem[50],n;
long long f(int x){//递归函数
    if(mem[x])return mem[x];
    else{
        mem[x]=f(x-1)+f(x-2);//调用自身
        return mem[x];
    }
}
int main(){
    cin>>n;
    mem[1]=1;
    mem[2]=1;
    cout<

诶？这里mem[]数组是什么？没错，它就是记忆化搜索！

为什么这么用？请看下图。

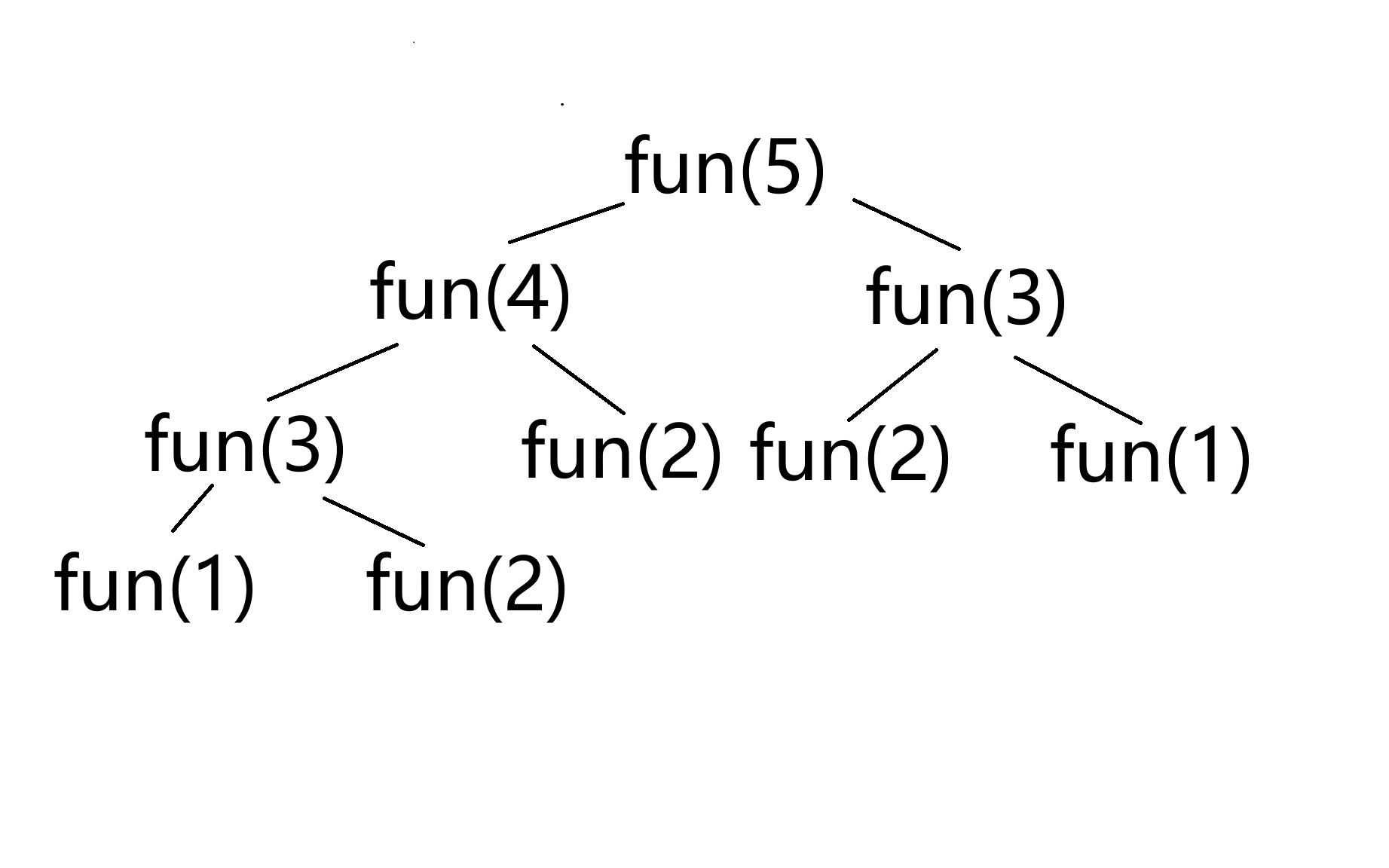注意看，fun(3)​和它的​分支子树都产生了重复，这时候再算一遍会非常浪费时间复杂度，所以可以存储并调用已计算的结果。mem数组是记录数据的数组。

最后，我挂一道思考题：

题目描述

上海世博会吉祥物海宝很讨人喜欢，聪明的海宝今天开始玩起了跳沙坑挖金币的游戏。

已知所有沙坑一字排开，依次编号为 1,2,3…，每个沙坑里面有若干金币，聪明的海宝开始不断地挖金币，在挖的过程中海宝发现了一个惊人的规律，第一个沙坑里面的金币数是 1，其余所有沙坑里的金币数和一些因素有关系：如果沙坑号 W 是奇数，那么该沙坑的金币数就是第 3×W+1 号沙坑的金币数加上 W；如果沙坑号 W 是偶数，那么该沙坑的金币数就是第 W/2 号沙坑的金币数加上 W。
如果问你第 n 号沙坑里面的金币数是多少，和海宝同样聪明的你能猜出来吗？

输入格式

一个正整数 n（1<=n<=100）

输出格式

第 n 号沙坑的金币数

输入输出样例

样例 1

输入样例 

10

输出样例 

46

数据范围与提示

第10号坑的金币数应该是第 5号坑的金币数加10，
第 5号坑的金币数应该是第16号坑的金币数加 5，
第16号坑的金币数应该是第 8号坑的金币数加16，
第 8号坑的金币数应该是第 4号坑的金币数加 8，
第 4号坑的金币数应该是第 2号坑的金币数加 4，
第 2号坑的金币数应该是第 1号坑的金币数加 2，
而第1号坑的金币数是已知的1。
反推回去第10号坑的数值应该是46。

​​​​（下一篇讲思考题）

到此结束！祝大家中秋快乐！国庆快乐！