题目呈现(源自2025年全国高中数学联赛(预赛)A卷)
题目5.若正整数 kkk 满足 (sin20∘+sin25∘⋅icos25∘+cos20∘⋅i)k∈R\left( \dfrac{\sin 20^\circ + \sin 25^\circ \cdot i}{\cos 25^\circ + \cos 20^\circ \cdot i} \right)^k \in \mathbb{R}(cos25∘+cos20∘⋅isin20∘+sin25∘⋅i)k∈R(iii为虚数单位),则kkk的最小值为______.
题目6.设 Γ\GammaΓ为任意正棱柱,在其12条棱中随机选取两条不同的棱l1,l2l_1, l_2l1,l2,事件“l1l_1l1 与 l2l_2l2平行”的概率记为P(Γ)P(\Gamma)P(Γ),则 P(Γ)P(\Gamma)P(Γ)的所有可能值为______.
题目7.平面中3个单位向量a⃗,b⃗,c⃗\vec{a},\vec{b},\vec{c}a,b,c 满足 a⃗−b⃗=[a⃗⋅c⃗]+[b⃗⋅c⃗]\vec{a} - \vec{b} = \left[ \vec{a} \cdot \vec{c} \right] + \left[ \vec{b} \cdot \vec{c} \right]a−b=[a⋅c]+[b⋅c]([x][x][x]表示不超过实数xxx的最大整数),则∣a⃗+b⃗+c⃗∣|\vec{a} + \vec{b} + \vec{c}|∣a+b+c∣的取值范围是______.
题目8.将 1,2,3,⋯ ,91,2,3,\cdots,91,2,3,⋯,9 排列为 a,b,c,d,e,f,g,h,ia,b,c,d,e,f,g,h,ia,b,c,d,e,f,g,h,i,使得三个三位数abc‾+def‾+ghi‾=2025\overline{abc} + \overline{def} + \overline{ghi} = 2025abc+def+ghi=2025,则不同的排列方法数为______.
破题思路
题目5:复数乘方入实域
破题点:看到分式复数的kkk次幂要求为实数,立即联想复数三角化与棣莫弗定理将复数转化为就是,目标r(cosθ+isinθ)r(\cos \theta + i \sin \theta)r(cosθ+isinθ)形式,从而利用辐角为kθk\thetakθ时虚部为零的条件.
题目6:棱柱平行概率谜
破题点:正棱柱的棱分三类——侧棱、上底棱、下底棱.平行关系仅存在于同类棱之间,且需分类讨论底面形状(平行四边形/梯形/一般四边形).
题目7:向量方程捉迷藏
破题点:由 a⃗−b⃗=[a⃗⋅c⃗]+[b⃗⋅c⃗]\vec{a} - \vec{b} = [\vec{a} \cdot \vec{c}] + [\vec{b} \cdot \vec{c}]a−b=[a⋅c]+[b⋅c] 且 [⋅][\cdot][⋅]是取整函数,分析出a⃗−b⃗\vec{a} - \vec{b}a−b只能是整数,结合单位向量性质缩小范围.
题目8:数字排列拼2025
破题点:将 abc‾+def‾+ghi‾=2025\overline{abc} + \overline{def} + \overline{ghi} = 2025abc+def+ghi=2025 转化为各位数字和与进位制分析,关键锁定C=c+f+i=15C = c + f + i = 15C=c+f+i=15.
关键推导与解答
题目5:复数乘方入实域
破题点:复数三角化与棣莫弗定理
这个分式复数长得像一团乱麻,但分母分子都是三角函数线性组合——和差化积公式瞬间让问题清爽起来!
原式化简:
sin20∘+isin25∘cos25∘+icos20∘=sin20∘cos20∘+sin25∘cos25∘⋅icos20∘cos25∘=sin40∘+isin50∘2cos20∘cos25∘=12cos20∘cos25∘(cos50∘+isin50∘)\small{ \begin{align*} & \dfrac{\sin 20^\circ + i \sin 25^\circ}{\cos 25^\circ + i \cos 20^\circ} \\ = & \dfrac{\sin 20^{\circ}\cos 20^{\circ}+\sin 25^{\circ}\cos 25^{\circ}\cdot i}{\cos 20^{\circ}\cos 25^{\circ}} \\ = & \dfrac{\sin 40^\circ + i \sin 50^\circ}{2 \cos 20^\circ \cos 25^\circ} \\ = & \dfrac{1}{2 \cos 20^\circ \cos 25^\circ} (\cos 50^\circ + i \sin 50^\circ) \end{align*}}===cos25∘+icos20∘sin20∘+isin25∘cos20∘cos25∘sin20∘cos20∘+sin25∘cos25∘⋅i2cos20∘cos25∘sin40∘+isin50∘2cos20∘cos25∘1(cos50∘+isin50∘)
此处用到了 sinAcosB+cosAsinB=sin(A+B)\sin A \cos B + \cos A \sin B = \sin(A+B)sinAcosB+cosAsinB=sin(A+B) 的变形)
于是原复数化为:
z=12cos20∘cos25∘⋅(cos50∘+isin50∘)\small{z = \dfrac{1}{2 \cos 20^\circ \cos 25^\circ} \cdot (\cos 50^\circ + i \sin 50^\circ)}z=2cos20∘cos25∘1⋅(cos50∘+isin50∘)
它的 kkk 次幂为:
zk=1(2cos20∘cos25∘)k(cos50k∘+isin50k∘)\small{z^k = \dfrac{1}{(2 \cos 20^\circ \cos 25^\circ)^k} (\cos 50k^\circ + i \sin 50k^\circ)}zk=(2cos20∘cos25∘)k1(cos50k∘+isin50k∘)
关键一击:zk∈Rz^k \in \mathbb{R}zk∈R当且仅当虚部为零,即sin50k∘=0\sin 50k^\circ = 0sin50k∘=0.
解得 50k=180∘⋅m50k = 180^\circ \cdot m50k=180∘⋅m(mmm为整数),即k=18m5k = \dfrac{18m}{5}k=518m.
最小正整数 kkk 需满足 5∣18m5 \mid 18m5∣18m,故 m=5m=5m=5 时,k=18k=18k=18.
✅ 本题精要:
- 三角恒等式化简分式复数
- 棣莫弗定理处理乘幂
- 虚部归零求整数解
题目6:棱柱平行概率谜
破题点:分类讨论底面形状
四棱柱的12条棱看似杂乱,实则侧棱相互平行,看上下底面情况
情形1:底面为一般四边形(两组对边都不平行):
P(Γ)=C42×2+C42C122=6×2+666=533\begin{align*} P(\Gamma) &= \dfrac{C_{4}^{2} \times 2 + C_{4}^{2}}{C_{12}^{2}} \\ & = \dfrac{6 \times 2 + 6}{66} = \dfrac{5}{33} \end{align*}P(Γ)=C122C42×2+C42=666×2+6=335
情形2:底面为梯形(一组对边平行):
P(Γ)=C42+C42+C42×2C122=6+6+1266=733\begin{align*} P(\Gamma) &= \dfrac{C_{4}^{2} + C_{4}^{2} + C_{4}^{2} \times 2}{C_{12}^{2}} \\ &= \dfrac{6 + 6 + 12}{66} = \dfrac{7}{33} \end{align*}P(Γ)=C122C42+C42+C42×2=666+6+12=337
情形3:底面为平行四边形(两组对边平行):
P(Γ)=C42+C42+C42C122=6+6+666=311\begin{align*} P(\Gamma) &= \dfrac{C_{4}^{2} +C_{4}^{2} + C_{4}^{2}}{C_{12}^{2}} \\ &= \dfrac{6 + 6 + 6}{66} = \dfrac{3}{11} \end{align*}P(Γ)=C122C42+C42+C42=666+6+6=113
✅ 本题精要:
- 解剖棱柱结构(侧棱/底棱)
- 分类讨论底面平行性(一般/梯形/平行四边形)
- 组合计数(CnkC_{n}^{k}Cnk的灵活应用)
题目7:向量方程捉迷藏
破题点:结合单位向量性质缩小范围
单位向量点积范围是[−1,1][-1,1][−1,1],取整后只有−1,0,1-1,0,1−1,0,1 三种可能.
由∣a⃗∣≤∣b⃗∣|\vec{a}|\leq|\vec{b}|∣a∣≤∣b∣,∣a⃗∣=1|\vec{a}|=1∣a∣=1及及及a⃗−b⃗=[a⃗−c⃗]+[b⃗−c⃗]∈Z\vec{a}-\vec{b}=[\vec{a}-\vec{c}]+[\vec{b}-\vec{c}]\in \mathbb{Z}a−b=[a−c]+[b−c]∈Z,
可知a⃗−b⃗∈{−1,0,1}\vec{a}-\vec{b}\in\{-1,0,1\}a−b∈{−1,0,1}.
分类讨论:
情形1:若a⃗−b⃗=1\vec{a}-\vec{b}=1a−b=1,
则a⃗=b⃗\vec{a}=\vec{b}a=b,此时[a⃗−c⃗]+[b⃗−c⃗]=2[a⃗−c⃗][\vec{a}-\vec{c}]+[\vec{b}-\vec{c}]=2[\vec{a}-\vec{c}][a−c]+[b−c]=2[a−c]为偶数,不可能为111,矛盾.
情形2:若a⃗−b⃗=−1\vec{a}-\vec{b}=-1a−b=−1,
则b⃗=−a⃗\vec{b}=-\vec{a}b=−a,此时∣a⃗+b⃗+c⃗∣=∣c⃗∣=1|\vec{a}+\vec{b}+\vec{c}|=|\vec{c}|=1∣a+b+c∣=∣c∣=1
相应的例子存在,例如c⃗\vec{c}c与a⃗\vec{a}a的夹角为锐角时,
由−1<−b⃗⋅c⃗<0<a⃗⋅c⃗<1-1<-\vec{b} \cdot \vec{c}<0<\vec{a} \cdot \vec{c}<1−1<−b⋅c<0<a⋅c<1,
知[a⃗−c⃗]+[b⃗−c⃗]=−1=a⃗−b⃗[\vec{a}-\vec{c}]+[\vec{b}-\vec{c}]=-1=\vec{a}-\vec{b}[a−c]+[b−c]=−1=a−b.
情形3:若a⃗−b⃗=0\vec{a}-\vec{b}=0a−b=0,
不妨设a⃗=(1,0)\vec{a}=(1,0)a=(1,0),b⃗=(0,1)\vec{b}=(0,1)b=(0,1),c⃗=(cosθ,sinθ)\vec{c}=(\cos\theta,\sin\theta)c=(cosθ,sinθ),θ∈[0,2π)\theta\in[0,2\pi)θ∈[0,2π).
记f(θ)=[a⃗−c⃗]+[b⃗−c⃗]=[cosθ]+[sinθ]f(\theta)=[\vec{a}-\vec{c}]+[\vec{b}-\vec{c}]=[\cos\theta]+[\sin\theta]f(θ)=[a−c]+[b−c]=[cosθ]+[sinθ].
当θ=0\theta=0θ=0或π2\dfrac{\pi}{2}2π时,f(θ)=1≠0f(\theta)=1\neq 0f(θ)=1=0,
当θ∈(π2,π)\theta\in(\dfrac{\pi}{2},\pi)θ∈(2π,π)时,f(θ)<0f(\theta)<0f(θ)<0,均不合要求.
当θ∈(0,π2)\theta\in(0,\dfrac{\pi}{2})θ∈(0,2π)时,f(θ)=0f(\theta)=0f(θ)=0,满足要求,此时
∣a⃗+b⃗−c⃗∣=(1+cosθ)2+(1+sinθ)2=3+22sin(θ+π4)∈(5,2+1].\begin{align*} &|\vec{a}+\vec{b}-\vec{c}| \\ =& \sqrt{(1+\cos\theta)^{2}+(1+\sin\theta)^{2}} \\ =&\sqrt{3+2\sqrt{2}\sin(\theta+\frac{\pi}{4})}\\ \in& (\sqrt{5},\sqrt{2}+1]. \end{align*}==∈∣a+b−c∣(1+cosθ)2+(1+sinθ)23+22sin(θ+4π)(5,2+1].
综上,∣a⃗+b⃗−c⃗∣|\vec{a}+\vec{b}-\vec{c}|∣a+b−c∣的取值范围是{1}∪(5,2+1]\{1\} \cup(\sqrt{5},\sqrt{2}+1]{1}∪(5,2+1].
✅ 本题精要:
取整函数性质(值域为{−1,0,1}\{-1,0,1\}{−1,0,1})
向量关系分类(平行或正交)
三角参数化求范围
题目8:数字排列拼2025
破题点:转化为各位数字和与进位制分析
由题意得
(100a+10b+c)+(100d+10e+f)+(100g+10h+i)=2025\tiny{(100a+10b+c)+(100d+10e+f)+(100g+10h+i)=2025}(100a+10b+c)+(100d+10e+f)+(100g+10h+i)=2025
即
100(a+d+g)+10(b+e+h)+(c+f+i)=2025\scriptsize{100(a + d + g) + 10(b + e + h) + (c + f + i) = 2025}100(a+d+g)+10(b+e+h)+(c+f+i)=2025
记
A=a+d+g,B=b+e+h,C=c+f+i,\begin{align*} A &=& a + d + g,\\ B &=& b + e + h,\\ C &=& c + f + i, \end{align*}ABC===a+d+g,b+e+h,c+f+i,
则
100A+10B+C=2025A+B+C=1+2+⋯+9=45\begin{align*} &100A + 10B + C = 2025\\ &A + B + C =1+2+\cdots+9 = 45 \end{align*}100A+10B+C=2025A+B+C=1+2+⋯+9=45
注意:CCC是末位和,且202520252025 末位为555,故 CCC 末位为555(可能进位).
但 1+2+3≥C≤9+8+7=241+2+3 \geq C \leq 9+8+7=241+2+3≥C≤9+8+7=24,
故 C=15C = 15C=15.
则 A+B=30A+B=30A+B=30且100A+10B=2010100A + 10B = 2010100A+10B=2010,
解得A=19A=19A=19,B=11B=11B=11.
接下来是 排列组合大作战:
{a,d,g}\{a,d,g\}{a,d,g} 和为191919,{b,e,h}\{b,e,h\}{b,e,h} 和为111111,{c,f,i}\{c,f,i\}{c,f,i} 和为151515,只需枚举191919和111111的拆分方案(每组数来自1∼91 \sim 91∼9且不重复):
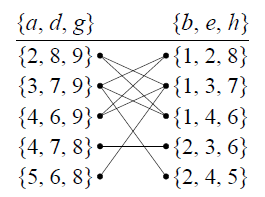
计算总数:
每组拆分中:
{a,d,g}\{a,d,g\}{a,d,g} 有 3!=63! = 63!=6 种排列
{b,e,h}\{b,e,h\}{b,e,h} 有 3!=63! = 63!=6 种排列
{c,f,i}\{c,f,i\}{c,f,i} 有 3!=63! = 63!=6 种排列
故总数 =9×63=1944= 9 \times 6^3 = 1944=9×63=1944.
✅ 本题精要:
各位和分解(A+B+C=45A+B+C=45A+B+C=45)
末位锁定 C=15C=15C=15
枚举不重复拆分
全排列乘法
答案汇总
| 题目 | 答案 |
|---|---|
| 题5 | 181818 |
| 题6 | 533, 733, 311\dfrac{5}{33},\ \dfrac{7}{33},\ \dfrac{3}{11}335,337,113 |
| 题7 | {1}∪(5,2+1]\{1\} \cup \left( \sqrt{5}, \sqrt{2} + 1 \right]{1}∪(5,2+1] |
| 题8 | 194419441944 |
笔锋破题,心向星辰;竞赛路上,拼搏向前!




 浙公网安备 33010602011771号
浙公网安备 33010602011771号