kmp算法详解

kmp

什么是kmp

kmp算法是一种字符串匹配算法，它对朴素模式匹配算法（时间复杂度 O(n*m)）进行了改进，极大的减少了无用的匹配次数，降低时间复杂度（时间复杂度变为O(n+m)），提高算法效率。

什么叫kmp

该名字是由它的三位发明人的名字的缩写组成。(Knuth，Morris,Pratt)

kmp算法中的相关概念

• 字符串s：一般成为主串，即比较长的字符串
• 字符串p：一般成为模式串，即比较短的字符串
• 模式匹配：模式匹配问题就是在给定的字符串（字符串s）中，找到与模式串（字符串p）相匹配的子串。（这里的匹配可以理解为相等）
• 字符串的前缀：指不包含最后一个字符的，所有字符的组合
• 字符串的后缀：指不包含第一个字符的，所有字符的组合
• 部分匹配值：字符串的前缀和后缀的最长相等的长度
• next数组：next数组是“部分匹配值表”，它存储的是每一个下标对应的“部分匹配值”，是KMP算法的核心。
• next[j + 1] 的含义：在模式串的第 j + 1个字符与主串第i个字符不匹配时，则模式串的下标移动到 next[j] 的位置，再与主串的当前位置（第i个字符）进行比较。

kmp的核心思想：：在每次不匹配时，主串s的指针不动，把模式串p的指针移动到 下一次匹配时可以和前面部分匹配的位置(next[j])，这样就可以跳过大多数的无意义的匹配步骤。

匹配思路和实现代码

KMP主要分两步：1. 求next数组、2. 匹配字符串。

1. s串 和 p串的字符的下标都是从1开始的。i(主串的下标) 从1开始，j(模式串的下标) 从0开始，每次s[ i ] 和p[ j + 1 ]进行比较。

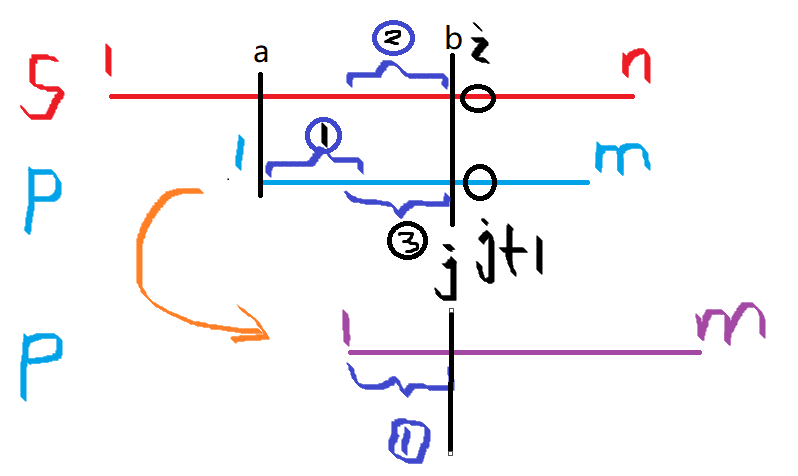
2. 当匹配过程到上图所示时，s[ a , b ] = p[ 1, j ] && s[ i ] != p[ j + 1 ] 此时要移动p串（注意：并不是只移动一次，而是移动到下次能匹配的位置）

3. 其中①串为[ 1, next[ j ] ]，③串为[ j - next[ j ] + 1 , j ]。由前后缀相等可知 ①串等于③串，③串又等于②串。所以直接移动p串使①到③的位置即可。这个操作可由j = next[ j ] 直接完成。

4. 如此往复下去，当 j == m时匹配成功。

匹配代码如下：

   //匹配过程，主串下标从1开始，模式串下标从0开始
//  n表示主串的长度  m表示模式串的长度
    for i,j := 1,0;i <= n;i++{
// 当 主串的字符s[i] 与 模式串的p[j+1]不匹配时，计算出p[0] -> p[j] 这段字符串的最长相等前后缀的长度，
// 然后将当前的 j 指向相应的位置（next[j]），模式串下标回溯到next[j] 这个位置
         for j > 0 &&  (j == m || s[i] != p[j+1]){ // j > 0（模式串第一个字符除外 next[1] = 0）
            j = next[j]
        }
        if s[i] == p[j+1] { //如果两个字符匹配，则模式串指针向后移动
            j++
        }
        if j == m{ 
       //匹配成功，可进行其他相关操作
            
        }
    }

注意：

1. 初始输出时，主串s和模式串p 的字符的下标是从1开始更容易写代码，会免去考虑很多边界条件。

2. 正因为第1 点，所以在进行匹配时，i是从1开始的，j 是从0开始的，要想比较相对应的两个字符，则必须是 s[i]与p[j + 1]进行比较。

求next数组的思路和实现代码

next数组的求法是通过模式串自己与自己进行匹配操作得出来的（代码和匹配操作几乎一样）。

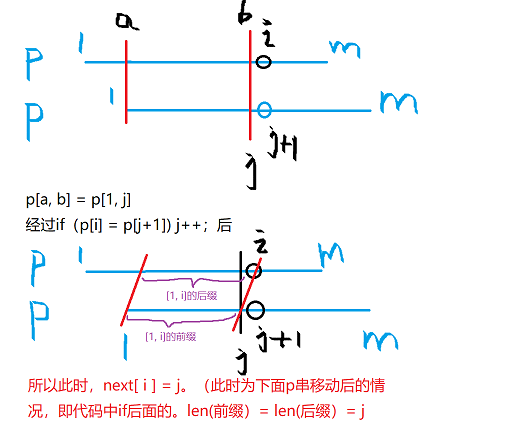
next求解代码如下

    // next数组的求法是通过模式串自己与自己进行匹配操作得出来的（代码和匹配操作几乎一样）
    // next[1] = 0  当 i=1 时，是没法求next数组的，因为next[1]的值为 下标为0 的一个字符的最长相等前后缀长度（它根本没有前后缀），因此 i 的下标从2开始
    for i,j:=2,0;i< m;i++{   
        for j > 0 && p[i] != p[j+1] {  
            j = next[j]
        }
        if p[i] == p[j+1]{ 
            j++
        }
        next[i] = j
    }

代码和匹配操作的代码几乎一样，关键在于每次移动 i 前，将 i 前面已经匹配的长度记录到 next数组中。

完整代码如下：

相关题目：LeetCode 28. 找出字符串中第一个匹配项的下标

func strStr(s string, p string) int {
    //kmp算法，下标一般从1开始，
    //next[j]数组 的值为 0到j-1 的字符串的最长相等前后缀的长度
    n:=len(s)
    m:=len(p)
    s = " "+ s
    p = " "+ p  //为了使得字符下标从1开始，方便操作
    next:=make([]int,m+1)
    
    // next数组的求法是通过模式串自己与自己进行匹配操作得出来的（代码和匹配操作几乎一样）
    // next[1] = 0  当 i=1 时，是没法求next数组的，因为next[1]的值为 下标为0 的一个字符的最长相等前后缀长度（它根本没有前后缀），因此 i 的下标从2开始
    for i,j:=2,0;i< m;i++{   
        for j > 0 && p[i] != p[j+1] {  
            j = next[j]
        }
        if p[i] == p[j+1]{ 
            j++
        }
        next[i] = j
    }
   
    //匹配过程，主串下标从1开始，模式串下标从0开始
    for i,j := 1,0;i <= n;i++{
// 当 主串的字符s[i] 与 模式串的p[j+1]不匹配时，计算出p[o] -> p[j] 这段字符串的最长相等前后缀的长度，
// 然后将当前的 j 指向相应的位置（next[j]），模式串下标回溯到next[j] 这个位置
        for j > 0 &&  (j == m || s[i] != p[j+1]){ // j > 0（模式串第一个字符除外 next[1] = 0）
            j = next[j]
        }
        if s[i] == p[j+1] { //如果两个字符匹配，则模式串指针向后移动
            j++
        }
        if j == m{ //如果模式串指针已经移动到最后位置，则表示全部匹配成功，返回
            return i-m
        }
    }
    return -1
}