Treap学习笔记
什么是treap
treap = 二叉搜索树 + 堆
treap 这个单词是 tree 和 heap 的组合,表明 treap 是一种由树和堆组合形成的数据结构。
二叉搜索树(BST)的性质
- 当前节点的左子树中的任何一个点的权值 < 当前点的权值
- 当前节点的右子树中的任何一个点的权值 > 当前点的权值
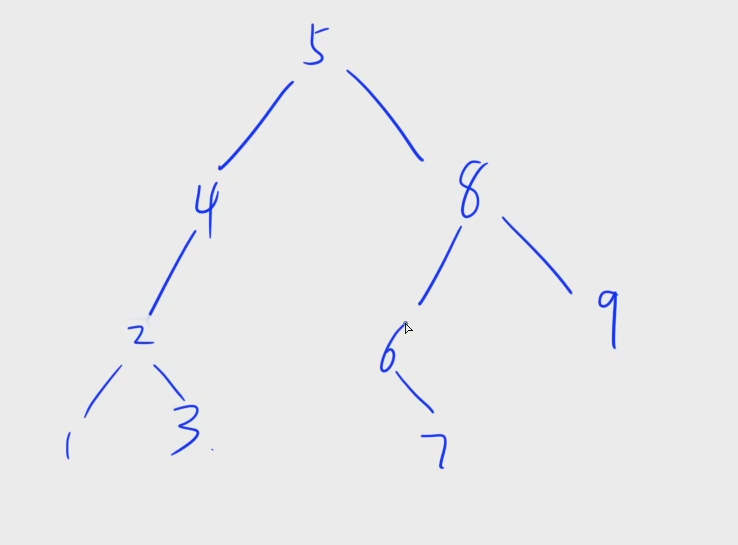
BST 中序遍历: 1,2,3,4,5,6,7,8,9 (一定是一个从小到大的)
BST 本质上就是在维护一个有序序列
前驱: 中序遍历的前一个位置
后继:中序遍历的后一个位置
BST的基本操作:
- 插入
- 删除
- 找前驱/后继
- 找最大最小
(以上可以由map或者set实现)
- 求某个值的排名
- 比某个数小的最大值
- 比某个数大的最小值
Treap的分类
1. 有旋式Treap
旋转 treap 在做普通平衡树题的时候,是所有平衡树中常数较小的。维护平衡的方式为旋转。性质与通二叉搜索树类似。因为普通的二叉搜索树会被递增或递减的数据卡,用 treap 对每个节点定义一个权值,由随机函数rand得到,从而防止特殊数据卡。treap 的每个结点上要额外储存一个值val 。treap 除了要满足二叉搜索树的性质之外,还需满足父节点的val大于等于两个儿子的val。而val是每个结点建立时随机生成的,因此 treap 是期望平衡的。
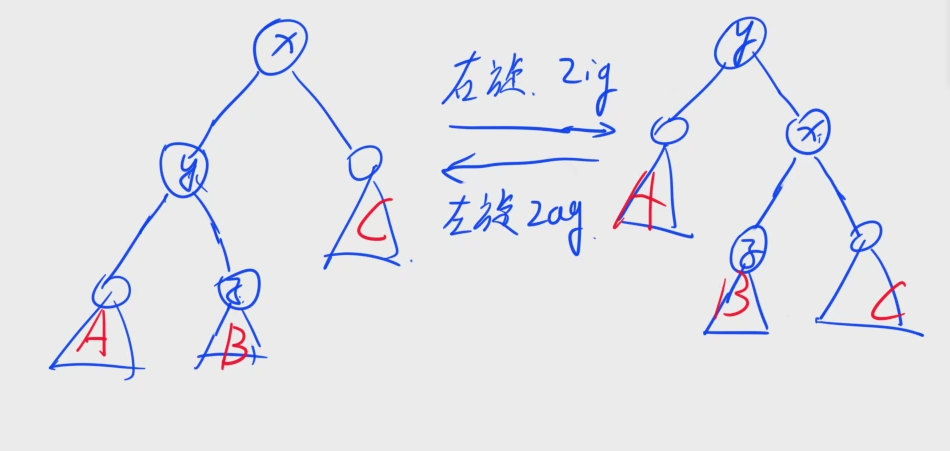
有旋Treap维护平衡的方式为旋转。性质与普通二叉搜索树类似。
下面是普通平衡树模板代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10,INF=1e9;
int n;
struct node{
int l,r; //左右儿子
int key,val;//节点值,平衡因子
int cnt,siz;//节点值得个数,子树的大小
}tr[N];
int root,tot=0;
void pushup(int p){
tr[p].siz=tr[tr[p].l].siz+tr[tr[p].r].siz+tr[p].cnt;
}
int get_node(int key){
tr[++tot].key=key;
tr[tot].val=rand();
tr[tot].cnt=tr[tot].siz=1;
return tot;
}
//右旋
void zig(int &p){
int q=tr[p].l;
tr[p].l=tr[q].r;tr[q].r=p;p=q;
pushup(tr[p].r);
pushup(p);
}
//左旋
void zag(int &p){
int q=tr[p].r;
tr[p].r=tr[q].l;tr[q].l=p;p=q;
pushup(tr[p].l);
pushup(p);
}
void build(){
get_node(-INF);get_node(INF);
root=1,tr[1].r=2;
pushup(root);
if(tr[1].val<tr[2].val) zag(root);
}
//插入
void insert(int &p,int key){
if(!p) p=get_node(key);
else if(tr[p].key==key) tr[p].cnt++;
else if(tr[p].key>key){
insert(tr[p].l,key);
if(tr[tr[p].l].val>tr[p].val) zig(p);
}
else {
insert(tr[p].r,key);
if(tr[tr[p].r].val>tr[p].val) zag(p);
}
pushup(p);
}
//删除
void remove(int &p,int key){
if(!p) return;
if(tr[p].key==key) {
if(tr[p].cnt>1) tr[p].cnt--;
else if(tr[p].l||tr[p].r){
if(!tr[p].r||tr[tr[p].l].val>tr[tr[p].r].val){
zig(p);
remove(tr[p].r,key);
}
else {
zag(p);
remove(tr[p].l,key);
}
}
else p=0;
}
else if (tr[p].key > key) remove(tr[p].l, key);
else remove(tr[p].r, key);
pushup(p);
}
//当前值为k的排名第几
int get_rank_by_key(int p,int key){
if(!p) return 0;
if(tr[p].key==key) return tr[tr[p].l].siz+1;
if(tr[p].key>key) return get_rank_by_key(tr[p].l,key);
return tr[tr[p].l].siz+tr[p].cnt+get_rank_by_key(tr[p].r,key);
}
//找到第k小的值
int get_key_by_rank(int p,int rank){
if(!p) return INF;
if(tr[tr[p].l].siz>=rank) return get_key_by_rank(tr[p].l,rank);
if(tr[tr[p].l].siz+tr[p].cnt>=rank) return tr[p].key;
return get_key_by_rank(tr[p].r,rank-tr[tr[p].l].siz-tr[p].cnt);
}
//前驱
int get_prev(int p,int key){
if(!p) return -INF;
if(tr[p].key>=key) return get_prev(tr[p].l,key);
return max(tr[p].key,get_prev(tr[p].r,key));
}
//后继
int get_next(int p, int key) // 找到严格大于key的最小数
{
if (!p) return INF;
if (tr[p].key <= key) return get_next(tr[p].r, key);
return min(tr[p].key, get_next(tr[p].l, key));
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
build();
cin>>n;
while(n--){
int op,x;
cin>>op>>x;
if(op==1) insert(root,x);
else if(op==2) remove(root,x);
else if(op==3) cout<<get_rank_by_key(root,x)-1<<endl;
else if(op==4) cout<<get_key_by_rank(root,x+1)<<endl;
else if(op==5) cout<<get_prev(root,x)<<endl;
else cout<<get_next(root,x)<<endl;
}
}
无旋式fhq-Treap
无旋式 treap 又称分裂合并 treap。它仅有两种核心操作,即为分裂与合并。无旋式 treap 的操作方式使得它天生支持维护序列、可持久化等特性。
优点
- FHQ Treap 的优点,好理解,上手快,代码一般很短,可持久化等。
- 是不用旋转。
FHQ Treap 同时也借用了Treap 的特点,每一个节点拥有两个权值,一个是二叉树权值 tree,另一个是 heap。其次,它基于两个操作,一个是分裂 Split,另一个是合并Merge。
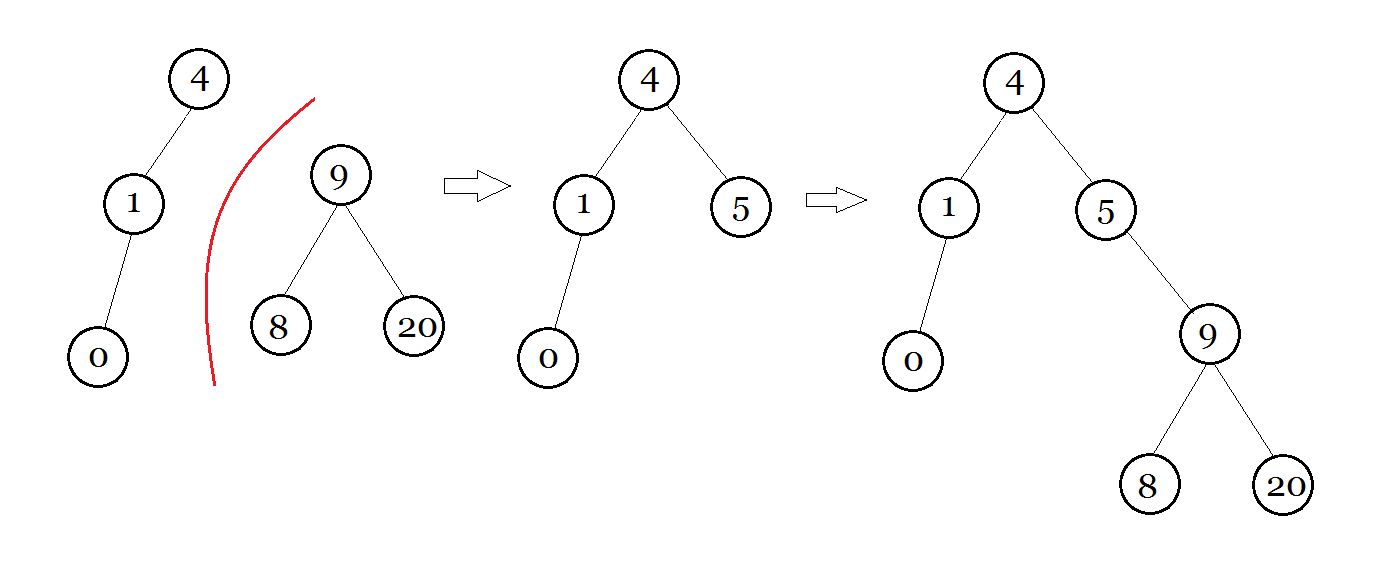
Split
split 的意思就是将这颗二叉树按某种条件掰开两半。这道题是按权值的大小掰开。假如一棵树要以 6 来掰开,如图 : (下方都是 tree值)
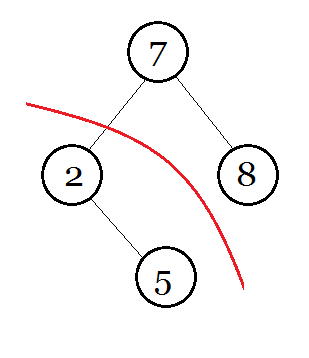
被掰成两半
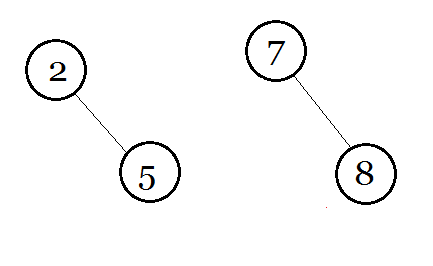
约定 : 分裂后左边的树为 x,右边的树为 y,它们的根为 X 和 Y。
那么合并呢? 就是大力将两棵树合在一起。
void split(int p,int val,int &x,int &y){
if(!p) x=y=0;
else{
if(fhq[p].val<=val){
x=p;
//有可能x的的右边的儿子的权值大于val
split(fhq[p].r,val,fhq[p].r,y);
}
else{
y=p;
//有可能y的的右边的儿子的权值大于val
split(fhq[p].l,val,x,fhq[p].l);
}
pushup(p);
}
}
Merge
其实就是split逆操作
int merge(int x,int y){
if(!x||!y) return x+y;
if(fhq[x].key>fhq[y].key){// 随机值期望平衡
fhq[x].r=merge(fhq[x].r,y);
pushup(x);//合并后更新一下节点信息
return x;
}
else{
fhq[y].l=merge(x,fhq[y].l);
pushup(y);
return y;
}
}
插入
首先是插入一个数字 k。
我们想,如果我们按照 k 掰开整颗树,然后将 k 强行套进去,然后再合起来是不是就可以呢了。
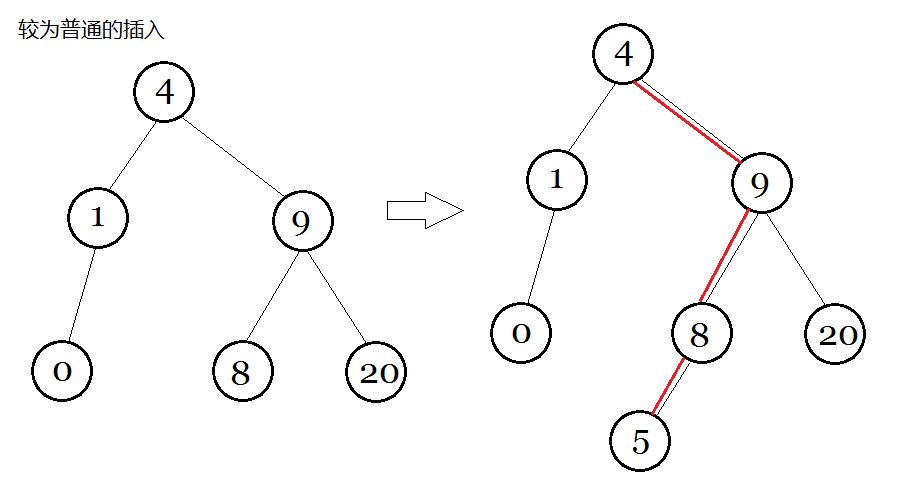
然后是fhq-treap的插入
void insert(int val){
int x,y;
split(root,val,x,y);//先将小于等于val的x为根树和大于val的以y为根的树分开
root=merge(merge(x,get_node(val)),y);//然后用新的节点与x合并形成新的树,然后再和y合并
}
删除
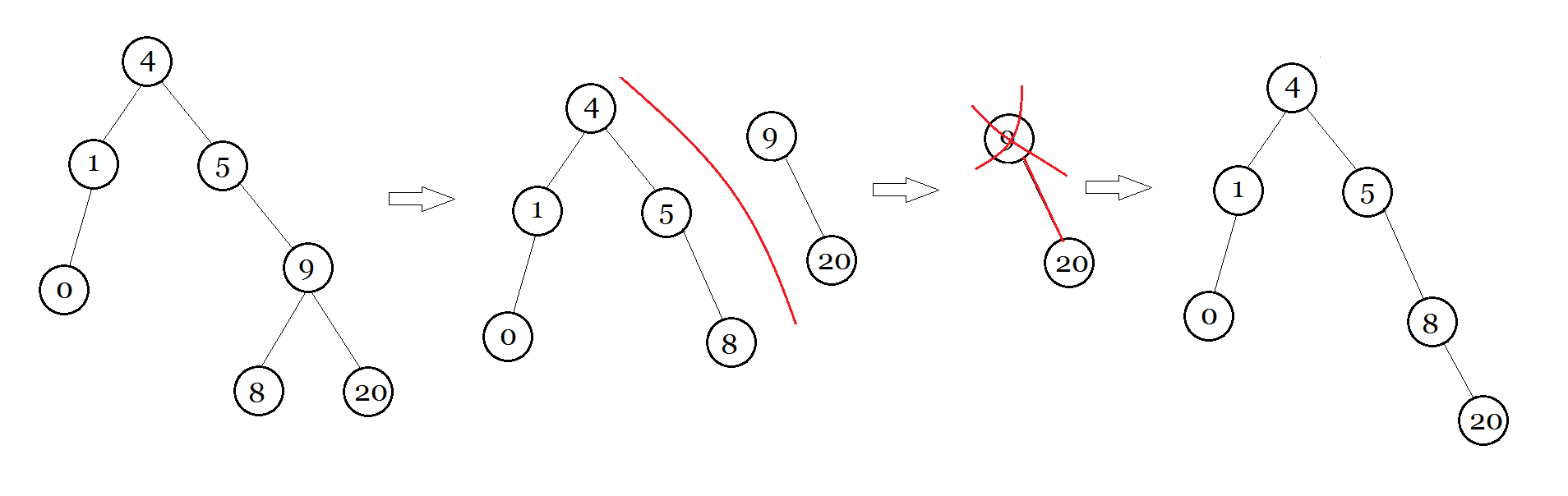
BST的删除比较麻烦,fhq treap可是嗨到不要不要的。
我们要删除节点k。
首先我们要把这棵树分成以 k 领导的树和非 k 领导的树,就是大力掰开。然后把以 k 领导的树的左儿子和右儿子合起来,将 k 丢入虚无。然后再合并新合成的树和非 k 领导的树。
图解 : (假如我们 Delete 9)
void del(int val){
int x,y,z;
split(root,val,x,z);//root树分裂成x,z树
split(x,val-1,x,y);//将x树分裂成x`,y树
y=merge(fhq[y].l,fhq[y].r);//将y树的根去掉,就是将其两个儿子合并
root=merge(merge(x,y),z);//最后在合并全部
}
求排名
我们再次大力掰开,把 k-1 这个点拿出来。这个时候根 \(x\) 都是 \(\leq k−1\) 的 (也就是 <\(k\))。然后我们把它的 size 拿出来,加个1就好了。
int getrank(int val){
int x,y;
split(root,val-1,x,y);//将val-1的树拆下来
int rk=fhq[x].size+1;//排名就是当前树size+1
root=merge(x,y);//不要忘了合并回去
return rk;
}
查询第k小
//只能普通方法来搞了
int getval(int rank){
int p=root;
while(p){
if(fhq[fhq[p].l].size+1==rank)
break;
else if(fhq[fhq[p].l].size>=rank)
p=fhq[p].l;
else{
rank-=fhq[fhq[p].l].size+1;
p=fhq[p].r;
}
}
return fhq[p].val;
}
求前驱
按照k-1掰开这颗树就可以保证这颗树都是\(<\)k的,然后找最大值(向右子树一直找)
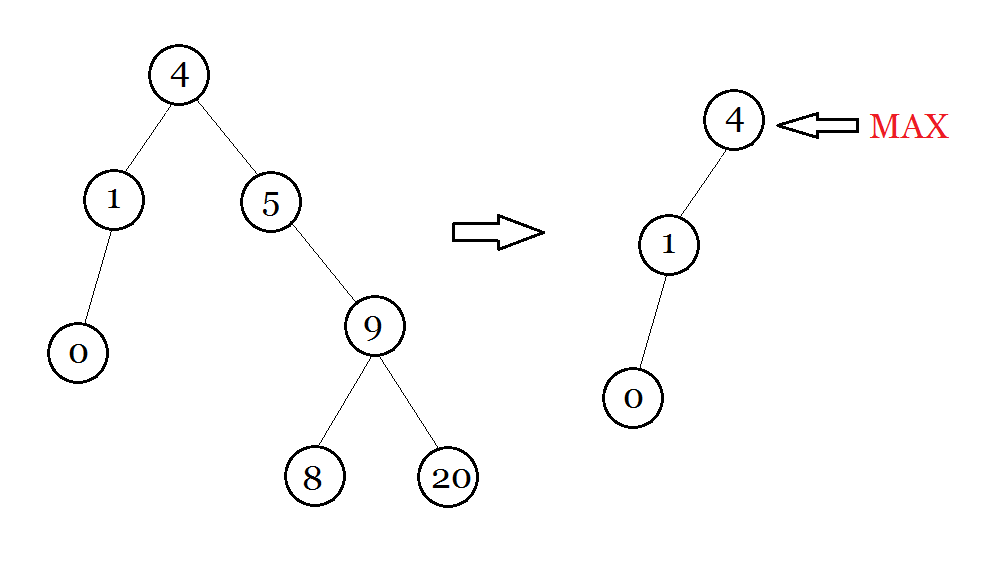
int getpre(int val){
int x,y;
split(root,val-1,x,y);//按照val-1掰开这颗树
int p=x;//要小于等于val的树
while(fhq[p].r) p=fhq[p].r;
root=merge(x,y);//不要忘了合并回去
return fhq[p].val;
}
求后继
同理
按照k掰开这颗树就可以保证这颗树都是\(>\)k的,然后找最大值(向左子树一直找)
int getnext(int val){
int x,y;
split(root,val,x,y);//按照val掰开这颗树
int p=y;//要大于val的树
while(fhq[p].l) p=fhq[p].l;
root=merge(x,y);//不要忘了合并回去
return fhq[p].val;
}
FHQ Treap模板
普通平衡树模板代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
struct node{
int l,r;
int val,key;
int size;
}fhq[N];
int tot,root;
std::mt19937 rnd(233); //随机数
int get_node(int val){
fhq[++tot].val=val;
fhq[tot].key=rnd();
fhq[tot].size=1;
return tot;
}
void pushup(int p){
fhq[p].size=fhq[fhq[p].l].size+fhq[fhq[p].r].size+1;
}
void split(int p,int val,int &x,int &y){
if(!p) x=y=0;
else{
if(fhq[p].val<=val){
x=p;
split(fhq[p].r,val,fhq[p].r,y);
}
else{
y=p;
split(fhq[p].l,val,x,fhq[p].l);
}
pushup(p);
}
}
int merge(int x,int y){
if(!x||!y) return x+y;
if(fhq[x].key>fhq[y].key){
fhq[x].r=merge(fhq[x].r,y);
pushup(x);
return x;
}
else{
fhq[y].l=merge(x,fhq[y].l);
pushup(y);
return y;
}
}
void insert(int val){
int x,y;
split(root,val,x,y);//先将小于等于val的x为根树和大于val的以y为根的树分开
root=merge(merge(x,get_node(val)),y);//然后用新的节点与x合并形成新的树,然后再和y合并
}
void del(int val){
int x,y,z;
split(root,val,x,z);//root树分裂成x,z树
split(x,val-1,x,y);//将x树分裂成x`,y树
y=merge(fhq[y].l,fhq[y].r);//将y树的根去掉,就是将其两个儿子合并
root=merge(merge(x,y),z);//最后在合并全部
}
int getrank(int val){
int x,y;
split(root,val-1,x,y);//将val-1的树拆下来
int rk=fhq[x].size+1;//排名就是当前树size+1
root=merge(x,y);//不要忘了合并回去
return rk;
}
//只能普通方法来搞了
int getval(int rank){
int p=root;
while(p){
if(fhq[fhq[p].l].size+1==rank)
break;
else if(fhq[fhq[p].l].size>=rank)
p=fhq[p].l;
else{
rank-=fhq[fhq[p].l].size+1;
p=fhq[p].r;
}
}
return fhq[p].val;
}
int getpre(int val){
int x,y;
split(root,val-1,x,y);//按照val-1掰开这颗树
int p=x;//要小于等于val的树
while(fhq[p].r) p=fhq[p].r;
root=merge(x,y);//不要忘了合并回去
return fhq[p].val;
}
int getnext(int val){
int x,y;
split(root,val,x,y);//按照val掰开这颗树
int p=y;//要大于val的树
while(fhq[p].l) p=fhq[p].l;
root=merge(x,y);//不要忘了合并回去
return fhq[p].val;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int n;
cin>>n;
while(n--){
int op,x;
cin>>op>>x;
if(op==1) insert(x);
else if(op==2) del(x);
else if(op==3) cout<<getrank(x)<<endl;
else if(op==4) cout<<getval(x)<<endl;
else if(op==5) cout<<getpre(x)<<endl;
else if(op==6) cout<<getnext(x)<<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号