第三天—C++语法基础

01递归的介绍

概念：递归是指函数直接或间接调用自身的过程

解释递归的两个关键要素：
①基本情况（递归终止条件）：满足时，递归终止，避免无线递归，解决极小规模问题
②递归表达式（递归调用）：用于解决规模更小的子问题，再将子问题的答案合并成当前问题的答案

02递归如何实现

返回类型 函数名（参数列表）{
	// 基本情况（递归终止条件）
	if (满足终止条件) {
		// 返回终止条件下的结果
	}
	// 递归表达式（递归调用）
	else {
		// 将问题分解为规模更小的子问题
		// 用递归调用解决子问题
		// 返回子问题的结果组合
	}
}

落实到具体实现，要走这三步：

1. 把大问题拆成规模更小的子问题；
2. 用递归调用逐个解决子问题；
3. 靠递归终止条件结束调用（避免无限套娃）。

几点注意：

• 必须保证递归能 “停下来”：无限递归会直接触发超时（TLE）、超内存（MLE）或运行错误（RE）；
• 边界条件可能不止一个：比如斐波那契的 n=0 和 n=1 都是终止条件；
• 别做重复计算：尽可能优化递归函数的性能（使用记忆化）

03递归和循环的比较

对比	递归	循环
核心思想	把大问题拆分为规模更小的子问题，通过函数自调用解决	通过重复执行一段代码块（for/while），靠循环条件终止，直接迭代完成计算
时间复杂度	纯递归易出现重复计算（如斐波那契纯递归时间复杂度 O (2ⁿ)），需记忆化优化至 O (n)	无函数调用，时间效率更高（如斐波那契迭代实现时间复杂度 O (n)）
适用场景	1.树和图的遍历2.快速排序等分治问题	1. 简单的重复计算（如斐波那契、累加）2. 递归层数过深的问题
注意点	1. 忘记写基线条件导致无限递归2. 未做记忆化导致超时3. 递归层数超限制（如部分 OJ 栈空间仅支持 1e4 层）	1. 循环条件写错导致死循环2. 中间结果存储不当（如数组越界）3. 初始值设置错误（如斐波那契迭代的 fb [1] 初始化）

04递归与汉诺塔

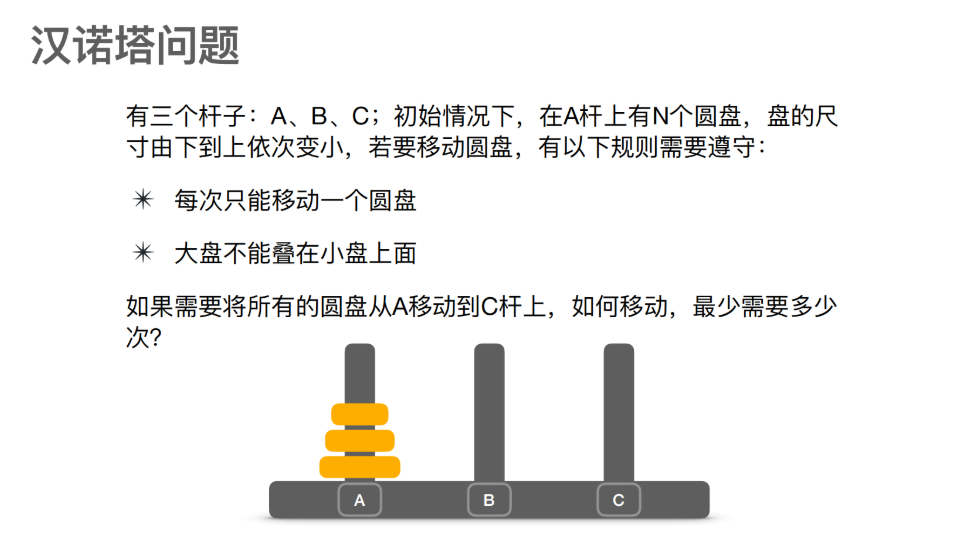
• 考虑只有1个盘子

  盘子可以从A直接到C
  

• 考虑有2个盘子

  第一个盘子先到从A->B,第二个盘子再从A->C,最后在B上的盘子再到C
  

• 3个盘子

  将上面两个看成一个整体，然后按照2个盘子考虑
  

• 多个盘子

  仍是3步，N个盘子分为两组：
  	前N个盘子
  	前N-1个盘子看成一个整体
  前N-1个盘子先从A柱到B柱，第N个盘子从A柱到C柱，最后前N-1盘子从B柱到C柱
  

• 代码实现

  void hanoi(int n, char a, char b, char c) {
      if (n == 1) {
          // 终止条件：只有1个圆盘时，直接从a移到c
          move(a, c);
      } else {
          // 步骤1：把n-1个圆盘从a移到b，以c为辅助
          hanoi(n - 1, a, c, b);
          // 步骤2：把第n个圆盘从a移到c
          move(a, c);
          // 步骤3：把n-1个圆盘从b移到c，以a为辅助
          hanoi(n - 1, b, a, c);
      }
  }
  

• 时间复杂度

  f(n) = 2ⁿ - 1
  

• 递归四要点

  1.明确终止条件（递归的 “出口”，如n=1）
  2.拆分出最小单元（单个圆盘的移动）
  3.建立递归关系（大问题依赖小问题的解）
  4.信任递归过程（无需深究嵌套细节，只需保证子问题逻辑正确）