09、Softmax回归

09、Softmax回归

1、.sum（）中0是对列求和，1是对行求和，如果X是一个形状为(2, 3)的张量，我们对列进行求和， 则结果将是一个具有形状(3,)的向量。 当调用sum运算符时，我们可以指定保持在原始张量的轴数，而不折叠求和的维度。 这将产生一个具有形状(1, 3)的二维张量。

X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
X.sum(0, keepdim=True), X.sum(1, keepdim=True)

2、实现Softmax

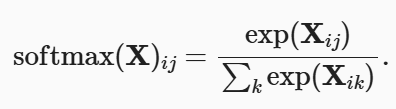
实现softmax由三个步骤组成：

1. 对每个项求幂（使用exp）；
2. 对每一行求和（小批量中每个样本是一行），得到每个样本的规范化常数；
3. 将每一行除以其规范化常数，确保结果的和为1。

def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition  # 这里应用了广播机制

X = torch.normal(0, 1, (2, 5))
X_prob = softmax(X)
X_prob, X_prob.sum(1)

(tensor([[0.1686, 0.4055, 0.0849, 0.1064, 0.2347],
         [0.0217, 0.2652, 0.6354, 0.0457, 0.0321]]),
tensor([1.0000, 1.0000]))

这里X是一个2行5列的矩阵，我个人理解为是有2类，5表示特征，把这个数据给Softmax，输出是一个概率值矩阵，每一行和为1。

3、W的大小：（输入特征数，输出类别数）；b的大小：（输出类别数，）

4、定义模型

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

• X.reshape((-1, W.shape[0]))

  • -1：让 PyTorch 自动计算这个维度的大小（通常是批次大小 batch_size），这里是256

  • W.shape[0]： 将这个维度的大小设置为 W 的第一个维度的大小，也就是输入特征数，这里是784。

• torch.matmul(A, W)

  • 对重塑后的输入 A（形状为 (batch_size, 输入特征数)）和权重 W（形状为 (输入特征数, 输出类别数)）进行矩阵乘法。这里A为（256，784），W为（784，10）
  • 计算结果： 得到一个形状为 (batch_size, 输出类别数) 的新张量。这个张量中的每个元素代表了某个样本属于某个类别的“原始分数”或“logits”。

• + b

  • 加上偏置向量 b。这里利用了 PyTorch 的广播机制。b 的形状是 (输出类别数,)，它会自动被加到 (batch_size, 输出类别数) 张量的每一行上。

5、定义损失函数——交叉熵损失函数

y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]

我们创建一个数据样本y_hat，其中包含2个样本在3个类别的预测概率， 以及它们对应的标签y。 有了y，我们知道在第一个样本中，第一类是正确的预测； 而在第二个样本中，第三类是正确的预测。 然后使用y作为y_hat中概率的索引， 我们选择第一个样本中第一个类的概率和第二个样本中第三个类的概率。

def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

cross_entropy(y_hat, y)