彻底弄清楚前缀和与差分！

前缀和

一维前缀和

普通求和

通常我们对一维数组求和采用的是从头到尾遍历的方式，时间复杂度是O(n)，但当计算很庞大的数据量时就很可能会超时！

int sum = 0;
for(int i = 0; i < nums.size(); i++)
	sum += nums[i]

一维前缀求和

1. 初始化前缀和数组（定义一个s[i]数组，用来记录(代表)前i项数据的和）:s[i] = s[i - 1] + a[i]

   

   注：i是从1开始的，这样就不用考虑边界问题了。如：s[1] = s[0] + a[1]，s[0] = 0

2. 查询操作：计算[l ~ r]的和：s[r] - s[l - 1]。时间复杂度是O(1)

【acwing.795前缀和】

输入一个长度为 n 的整数序列。

接下来再输入 m 个询问，每个询问输入一对 l,r。

对于每个询问，输出原序列中从第 ll 个数到第 rr 个数的和。

输入格式

第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

接下来 m 行，每行包含两个整数 ll 和 rr，表示一个询问的区间范围。

输出格式

共 m 行，每行输出一个询问的结果。

数据范围

1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000

输入样例：

5 3
2 1 3 6 4
1 2
1 3
2 4

输出样例：

3
6
10

【参考代码】

#include<iostream>

using namespace std;

int n,m;
const int N = 100000+10;
int a[N],s[N]; // 初始化数组了 a[0]、s[0]=0

int main()
{
    
    cin>>n>>m;
    for(int i = 1; i <= n; i++) cin>>a[i];
    
    //初始化前缀和数组s[i]
    for(int i = 1; i <= n; i++) s[i] = s[i -1] + a[i];
    
    int l, r;
    while(m--)
    {
        cin>>l>>r;
        //求[l~r]的和
        cout<<s[r] - s[l - 1]<<endl;
    }
    return 0;
}

二维前缀和(子矩阵的和)

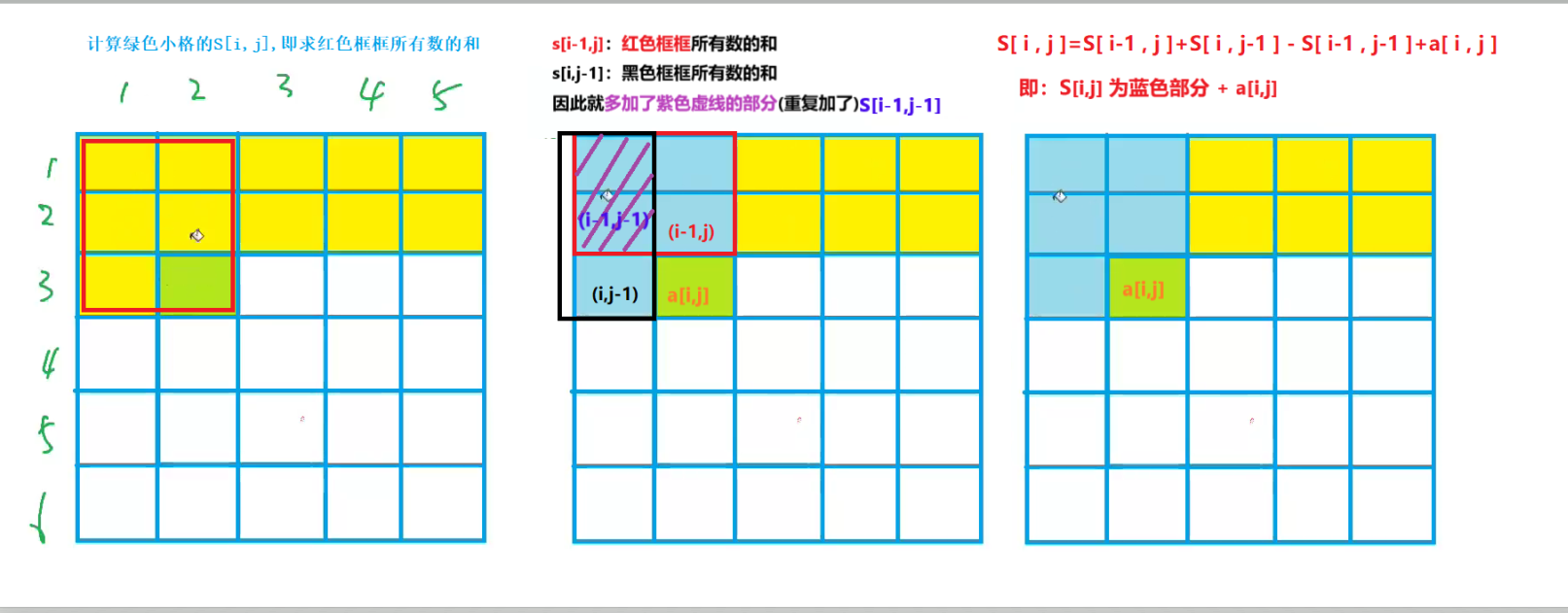
1. 初始化前缀和数组（定义一个二维s[i][j]数组，用来记录(代表)前(i,j)到原点所有数的和项数据的和）

   （1）S[i,j]是什么：S[i,j]即为图中绿色部分所有数的的和为：

   

   （2）S[i,j]怎么计算：S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j]

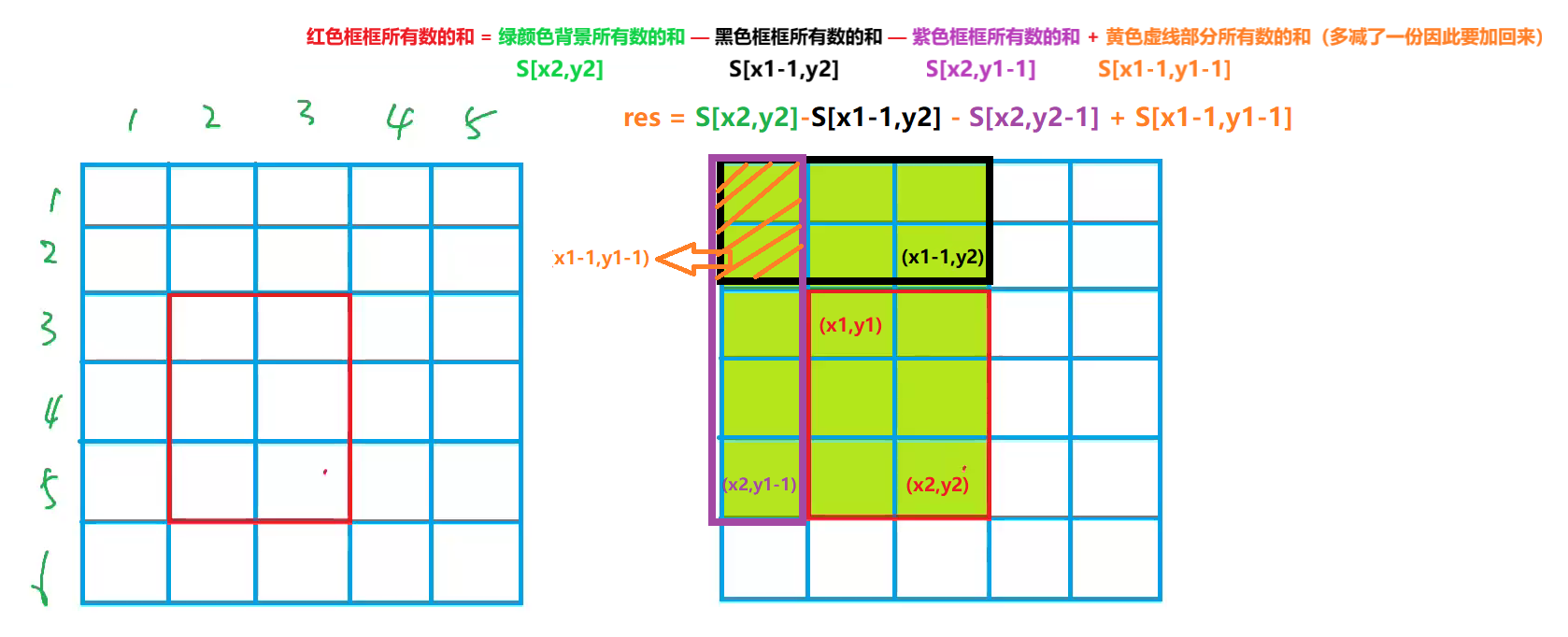
2. (x1，y1)，(x2，y2)这一子矩阵中所有数的和怎么计算?res = S[x2,y2]−S[x1−1,y2]−S[x2,y1−1]+S[x1−1,y1−1]

【acwing 796. 子矩阵的和】

输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数n，m，q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式

共 q 行，每行输出一个询问的结果。

数据范围

1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

【参考代码】

#include<iostream>

using namespace std;
const int N = 1000+10;
int a[N][N],s[N][N];

int main()
{
    int n,m,q;
    cin>>n>>m>>q;
    
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            scanf("%d",&a[i][j]);
            //1.初始化前缀和数组
            s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j]; 
        }
    }
    
    while(q--)
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1 , &y1, &x2, &y2);
        //2.计算(x1,y1)(x2,y2)子矩阵的和
        int res = s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1];
        printf("%d\n",res);
    }
    
    return 0;
}

注：

同一维前缀和为了不额外考虑边界问题我们从1开始对前缀和数组进行初始化。

当是大量数据的输入输出时scanf和printf运行的是比cin和cout要快的！(所用时间更少)

差分

类似于数学中的求导和积分，差分可以看成前缀和的逆运算。

一维差分

差分数组：

首先给定一个原数组a：a[1], a[2], a[3],,,,a[n];

然后我们要构造一个数组b ： b[1] ,b[2] , b[3],,,, b[i];

使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]

a数组是b数组的前缀和数组，反过来我们把b数组叫做a数组的差分数组。即，每一个a[i]都是b数组中从头开始到i的的一段区间和。

(1)如何构造差分b数组？

最为直接的方法

如下：

a[0 ]= 0;

b[1] = a[1] - a[0];

b[2] = a[2] - a[1];

b[3] =a [3] - a[2];

........

b[n] = a[n] - a[n-1];

两边各自相加得：b[1] + b[2] + ,,, + b[n] = a[n]

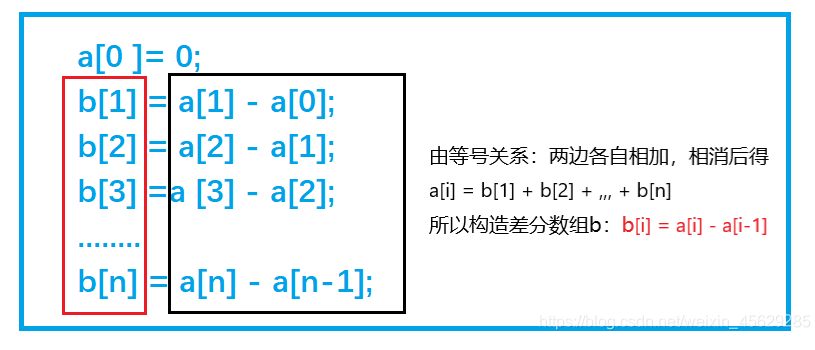
我们只要有b数组，最后通过前缀和运算，就可以在O(n) 的时间内得到a数组。

那我们构造出来的差分数组b到底有什么用？，看下面的解释你就了解啦！

(2)现在我们要给a数组在给定区间[l,r]上的每一个数加上c，即a[l] + c , a[l+1] + c , a[l+2] + c ,,,, a[r] + c。暴力的做法是for枚举l~r，时间复杂度是O(n)，如果我们需要对原数组执行m次这样的操作，时间复杂度就会变成O(n*m)。当数据量很庞大时很可能就会超时，那有没有更高效的方法呢？可以考虑一下差分操作！

始终要记得，a数组是b数组的前缀和数组对b数组的b[i]的修改，就一定会影响到a数组中从a[i]及往后的每一个数（图示理解这句话！）

通过上面的解释，那我们如何如和用差分数组b实现给a数组在[l,r]上+c呢？

• 首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c,,,,,, a[n] + c;（通过上面的例子我们知道对b[l]进行了修改(+c)，那么从l及后面所有的数都受到了影响(+c)），但我们想要的是给a数组在定区间[l,r]上+c，即多了从r+1开始到后面所有数，这一段数据）。

• 为此，我们打个补丁，b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,,,,,,,a[n] - c;（即b[r+1] - c完成了减去上述从r+1开始都后面多出来的数据）

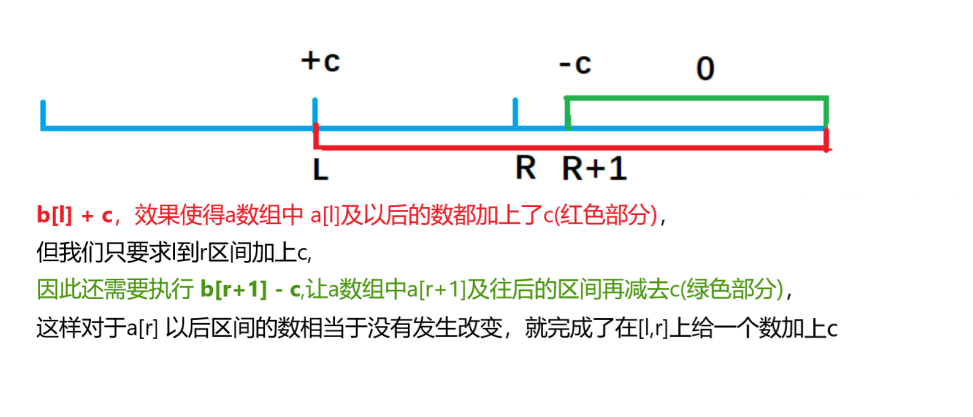
(3)如何求经过操作后的原数组a呢？

我们只要有了b数组，并对它进行b[l] += c，b[r + 1] -= c操作(使得a数组在[l,r]区间上每一个数+C)，最后通过对b数组进行前缀和运算，就可以在O(n) 的时间内得到a数组。

【acwing 797 差分】

输入一个长度为 n 的整数序列。

接下来输入 m个操作，每个操作包含三个整数l,r,c，表示将序列中 [l,r][l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数l，r，c，表示一个操作。

输出格式

共一行，包含 n 个整数，表示最终序列。

数据范围

1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000

输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

3 4 5 3 4 2

【参考代码】

#include<iostream>

using namespace std;
const int N = 100000+10;
int a[N],b[N];
int main()
{
	int n,m;
	cin>>n>>m;
	
	for(int i = 1; i <= n; i++)
	{
		scanf("%d",&a[i]);
		//构造差分数组
		b[i] = a[i] - a[i - 1]; 
	}
	
	//给a数组[l,r]上每一个数加上c  ===> b[l] += c, b[r+1] -= c
	while(m--)
	{
		int l,r,c;
		cin>>l>>r>>c;
		b[l] +=c;
		b[r + 1] -= c;	
	} 
	
	//求操作后的数组a———> 对b数组进行前缀和操作即可
	for(int i = 1; i <= n; i++)
	{
		 b[i] += b[i - 1];
		 printf("%d ",b[i]); 
	}
	
	return 0;
}

【一维差分总结】

给区间[l,r]上的每一个数加上c：b[l] += c，b[r + 1] -= c

二维差分

如果扩展到二维，我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是可以的，考虑二维差分。

a[][]数组是b[][]数组的前缀和数组，那么b[][]是a[][]的差分数组

原数组： a[i][j]

我们去构造差分数组： b[i][j]

使得a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。

（1）如何构造b数组呢？

我们去逆向思考。

同一维差分，我们构造二维差分数组目的是为了 让原二维数组a中所选中子矩阵中的每一个元素加上c的操作，可以由O(n*n)的时间复杂度优化成O(1)

在对子矩阵每一个数 + C操作之前，我们先要构造好差分数组b[i][j]

代码如下：

// 构造差分数组
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            b[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];
            

（2）那我们如何给子矩阵(x1,y1)，(x2,y2)中的每一个数都加上c呢？

已知原数组a中被选中的子矩阵为 以(x1,y1)为左上角，以(x2,y2)为右上角所围成的矩形区域;

始终要记得，a数组是b数组的前缀和数组，比如对b数组的b[i][j]的修改，会影响到a数组中从a[i][j]及往后的每一个数。

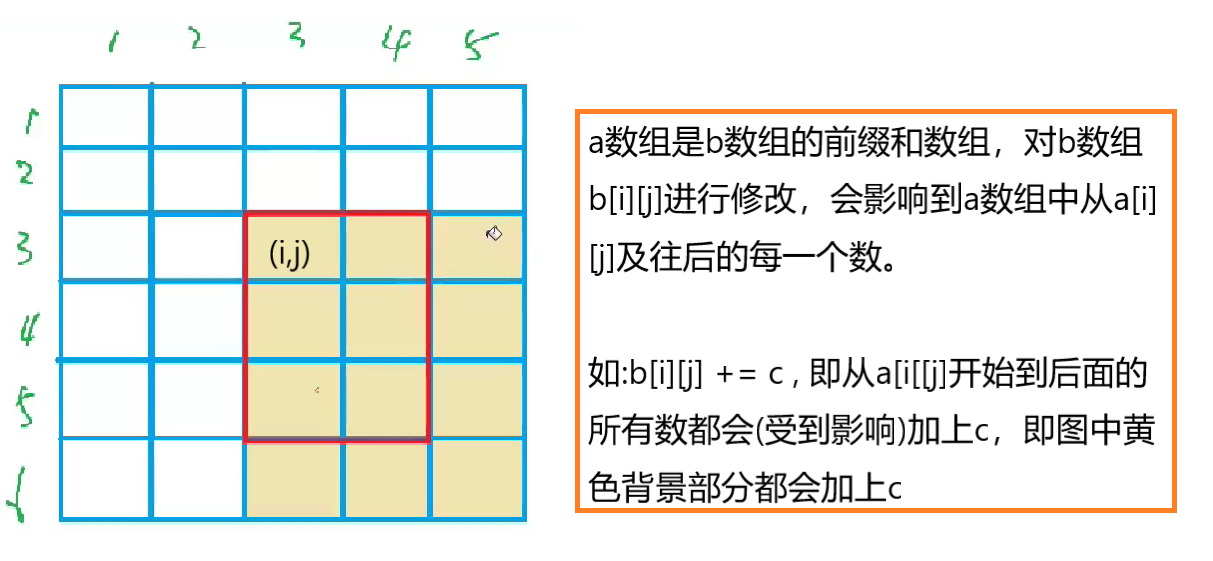
假定我们已经构造好了b数组，类比一维差分，我们执行以下操作
来使被选中的子矩阵中的每个元素的值加上c

b[x1][y1] + = c;

b[x1,][y2+1] - = c;

b[x2+1][y1] - = c;

b[x2+1][y2+1] + = c;

每次对b数组执行以上操作，等价于：

for(int i=x1;i<=x2;i++)
for(int j=y1;j<=y2;j++)
a[i][j]+=c;

我们画个图去理解一下这个过程：

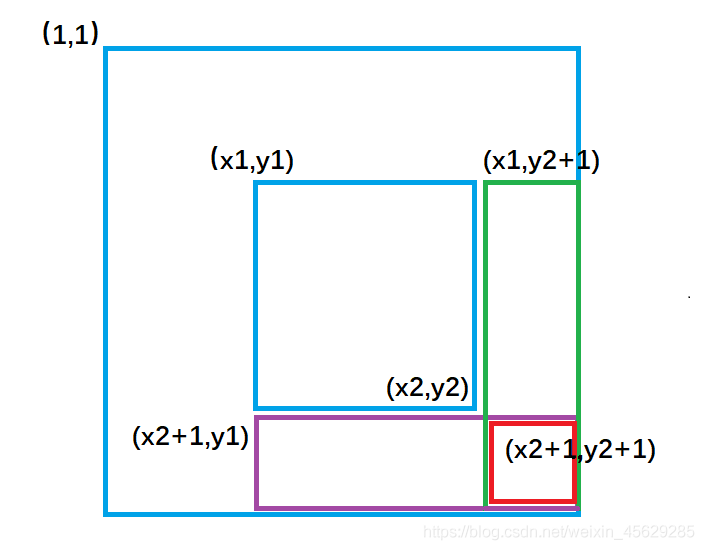
b[x1][ y1 ] +=c ; 对应图1 ,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1,][y2+1]-=c ; 对应图2 ,让整个a数组中绿色矩形面积的元素再减去c，使其内元素不发生改变。
b[x2+1][y1]- =c ; 对应图3 ,让整个a数组中紫色矩形面积的元素再减去c，使其内元素不发生改变。
b[x2+1][y2+1]+=c; 对应图4,,让整个a数组中红色矩形面积的元素再加上c，红色内的相当于被减了两次，再加上一次c，才能使其恢复。

我们将上述操作（子矩阵每一个数 + C）代码如下。时间复杂度O(1):

{   
	//对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了c
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}

（3）如何求经过操作后的原数组a呢？

当我们构造了二维差分数组b[i][j]，并对b[i][j]进行了 b[x1][y1]+=c; b[x2+1][y1]-=c; b[x1][y2+1]-=c; b[x2+1][y2+1]+=c;4个操作（使得a数组的子矩阵每一个数都加上了C），最后通过对b数组进行前缀和运算(二维前缀和运算)，就可以在短时间时间内得到a数组。

【acwing 798. 差分矩阵】

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 cc。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

** 输出格式**

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];

int main()
{
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);
// 构造差分数组
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            b[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];

    while (q -- )
    {
        int x1, y1, x2, y2, c;
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
        b[x1][y1] += c;
        b[x1][y2 + 1] -= c;
        b[x2 + 1][y1] -= c;
        b[x2 + 1][y2 + 1] += c;
    }
//  通过求差分数组b的前缀和来得到原数组a
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            b[i][j] = b[i][j] + b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; // 前缀和公式

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);
        cout << endl;
    }

    return 0;
}

总结：

1.先构造好一维或者二维差分数组

2.差分的作用：是在O(1)时间内给某一段区间[l,r]或者子矩阵(x1,y1)，(x2,y2)中的每一个数都加上C

注：如果文章有任何错误或不足，请各位大佬尽情指出，评论留言留下您宝贵的建议！如果这篇文章对你有些许帮助，希望可爱亲切的您点个赞推荐一手，非常感谢啦