KMP（Knuth-Morris-Pratt ）算法-模式串lps（Longest Prefix Suffix）最长相同前后缀长度数组算法证明

被KMP算法折磨了几天，终于搞明白lps数组，或者叫next数组计算过程中非常关键点的原理，这里着重在证明为什么这样计算。

 1 public static int[] buildLPS(String pat) {
 2     int n = pat.length();
 3     int[] lps = new int[n];
 4 
 5     int prefixLen = 0; // 当前已匹配的最长前后缀长度
 6     int i = 1;         // 正在处理 lps[i]
 7 
 8     while (i < n) {
 9         if (pat.charAt(i) == pat.charAt(prefixLen)) {
10             prefixLen++;
11             lps[i] = prefixLen;
12             i++;
13         } else if (prefixLen > 0) {
14             // 需要证明的部分
15             prefixLen = lps[prefixLen - 1];
16         } else {
17             lps[i] = 0;
18             i++;
19         }
20     }
21     return lps;
22 }

 

以上是计算lps数组的方法，lps数组表示了位于当前坐标i时，pat[0...i]中最长相同前后缀的长度。

line 9-13 说明了当pat[i] = pat[prelen]的时候，只需要继续沿用之前的最长前后缀长度就可以了

难点在理解line 15 为什么回退的时候 prefixLen=lps[prefixLen-1]而不是其他的值。以下是是证明过程：

当前len = lps[i-1]，及pat[0..i-1]的最长相同前后缀长度，及pat[0...len-1] = pat[i-len..i-1]。

当pat[len] != pat[i]时，表示不能继续沿用之前的len = lps[i-1]，

而是需要重新寻找一个t，满足pat[0...t-1]+pat[t] = pat[i-t...i-1]+pat[i]，相当于pat[0...t-1] = pat[i-t...i-1]，根据lps定义，及我们需要找一个pat[0...i-1]的长度为t且相同的前后缀。

已知len=lps[i-1]是不满足条件的，所以t<len。

目前

1. pat[0...len-1] = pat[i-len..i-1]

2. pat[0...t-1] = pat[i-t...i-1]

3. t<len

可知

pat[0...t-1]+pat[t..len-1] =pat[i-len..i-t-1]+pat[i-t...i-1]

由此可得 pat[i-t...i-1] （长度t) 是pat[0...len-1] = pat[0...t-1]+pat[t..len-1] 的后缀

又因为pat[0...t-1]（长度t) 是pat[0...len-1] 的前缀

所以t是pat[0...len-1]的某一个相同的前后缀的长度。

t的最大值是lps[len-1], 及pat[0..len-1]的最长相同前后缀长度。

 

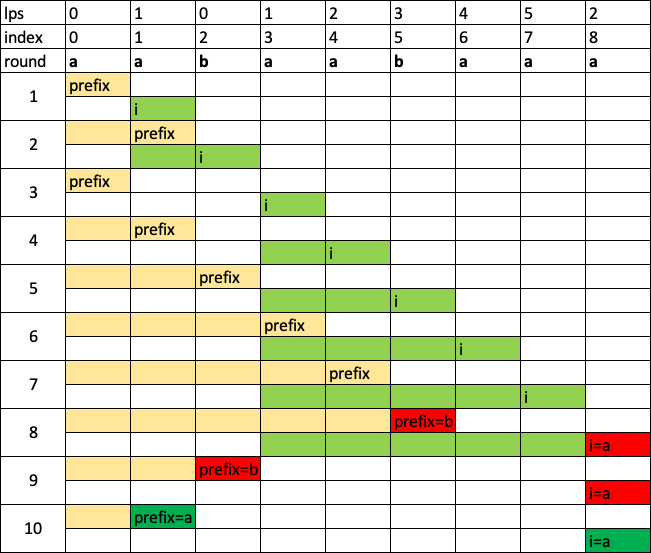
一个比较好体现这个过程的例子：aabaabaaa

lps是 [0, 1, 0, 1, 2, 3, 4, 5, 2]

 

image

 

 

 

 

 

 

 

posted on 2025-11-15 02:21  Lv Jianwei  阅读(0)  评论(0)    收藏  举报