矩阵理论
北航《矩阵理论与应用1》的不完全笔记,主攻一些基础概念
笔记主要参考赵迪老师上课内容以及王磊老师的那本教材,如有错误,欢迎指出
特殊矩阵
H 阵
Hermite matrix
定义
- \(A=A^H \in C^{n\times n}\)
判定
A是Hermite矩阵的充要条件
- ①存在酉矩阵 \(U\) 使得 \(U^HAU=\Lambda= \mathbf{diag}(\lambda_1,\cdots,\lambda_n)\)
\(\lambda_1,\cdots,\lambda_n\) 均为实数
- ②对任意方阵\(S\) ,\(S^HAS\) 为Hermite矩阵
- 如果 A , B 是Hermite阵,则\(AB\) 是Hermite矩阵的充要条件是\(AB=BA\)
性质
- 主对角线元素对角元为实数
- \(A=\begin{pmatrix}a_{11}&&&*\\&a_{22}&&\\&&\ddots&\\*&&&a_{nn}\end{pmatrix}A^H=\begin{pmatrix}\overline{a_{11}}&&&*\\&\overline{a_{22}}&&\\&&\ddots&\\*&&&\overline{a_{nn}}\end{pmatrix}\)
- \(A\) 有 \(n\) 个互相正交的特征向量,即 \(X_1\bot X_2\bot...\bot X_n\)
\(A\) 的不同特征值所对应的特征向量是相互正交的
- proof
![]()
- proof
- \(a_{i,j}=\overline{a_{j,i}}\)
\(1\leq i,j\leq n\)
- 任何实对称矩阵是Hermite矩阵
- 每个\(H\)阵\(A\) 优相似于对角阵
- 存在U阵 \(Q\) 使 \(Q^{-1}AQ=Q^HAQ=\Lambda=\begin{pmatrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{pmatrix}\\ A=Q\Lambda Q^{-1}=Q\Lambda Q^H\),且 \(\lambda(A)\in R\)
- proof
![]()
- proof
- 存在U阵 \(Q\) 使 \(Q^{-1}AQ=Q^HAQ=\Lambda=\begin{pmatrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{pmatrix}\\ A=Q\Lambda Q^{-1}=Q\Lambda Q^H\),且 \(\lambda(A)\in R\)
- 特征根都是实数,\(\{\lambda_1,\cdots,\lambda_n\}\in R\)
- proof
![]()
- proof
- 对正整数 \(k\),\(A^k\) 也是 \(H\) 阵
- 若 \(A\) 可逆,\(A^{-1}\) 也是 \(H\) 阵
- 对实数 \(k , p\) ,\(k A + p B\) 也是Hermite矩阵
(A , B为n 阶Hermite矩阵)
- 任一复方阵都可以唯一地表示成Hermite矩阵和反Hermite矩阵之和
乘积形式的H阵性质
- 对一切矩阵\(A=A_{n\times p}\) 且 \(n\geq p\) ,\(A^HA\)与\(AA^H\)都是Hermite阵
- proof
![]()
- proof
- \(AA^H\) 矩阵的迹
- \(A_{n\times p}=\begin{pmatrix}a_{11}&\cdots&a_{1p}\\\vdots&\ddots&\vdots\\a_{n1}&\cdots&a_{np}\end{pmatrix}\in C^{n\times p}\\ A_{p\times n}^H=\begin{pmatrix}\overline{a_{11}}&\cdots&\overline{a_{n1}}\\\vdots&\ddots&\vdots\\\overline{a_{1p}}&\cdots&\overline{a_{np}}\end{pmatrix}\in C^{p\times n}\)
- \(\displaystyle tr(A^HA)=tr(AA^H)=\sum\limits_{i=1,j=1}^n{|a_{ij}|^2}\)
- 推论
- \(tr(AB^H)=tr(B^HA)=\sum a_{ij}\overline{b_{ij}}\)
- \(A^HA\) 与 \(AA^H\)只相差 \(n-p\) 个 0 根
- proof
![]()
- proof
- \(A^HA\) 与 \(AA^H\) 是半正定阵
- proof
![]()
- proof
- \(r(AA^H)=r(A^HA)=r(A)=r(A^H)\)
- proof 1
![]()
- proof 2——只需证\(A^HAX= 0\) 的解也是 \(AX=0\) 的解
![]()
- proof 1
二次型、正定阵
参考来源 csdn
Hermite二次型定义
- 令 \(A^H=A\in \Bbb C^{n\times n}\),\(X=\begin{pmatrix}x_1\\x_2\\\vdots\\v_n \end{pmatrix}\)
- 称 \(X^HAX=(\overline{x_1},\overline{x_2},\cdots,\overline{x_n}) A\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}\\\)为矩阵 \(A\) 产生的二次型,记作 \(f(x)=X^HAX\)
正定二次型与正定阵定义
- 若\(A^H=A\) ,对一切\(X\neq0\) ,有\(X^HAX>0\) ,则\(f(x)=X^HAX\)为正定二次型,\(A\)为正定阵,记为 \(A>0\)
- 若\(A^H=A\) ,对一切\(X\neq0\) ,有\(X^HAX\geq0\) ,则\(f(x)=X^HAX\)为半正定二次型,A为半正定阵,记为 \(A\geq0\)
- 补充定义
![]()
判定\(n\)阶Hermite矩阵\(A\)正定
- all
![]()
正定阵定理
- \(A>0\Longleftrightarrow A\)为Hermite阵,且\(\lambda_1,\lambda_2,\cdots,\lambda_n>0\)
- proof
![]()
- proof
- \(A\geq0\iff A\)为Hermite阵,且\(\lambda_1,\lambda_2,\cdots,\lambda_n\geq0\)
- 单位阵是正定阵
- 正定阵间必合同
- \(A >0 \iff A \triangleq \Lambda\)
- \(\Lambda \triangleq I\)
- 若 \(A,B\) 为同阶正定阵,则 \(A \triangleq B\)
- proof
![]()
补充
- 实正定阵的重要结论
![]()
斜H阵
Skew-Hermit
- \(A^H=-A\)
- 性质
- 对角元为纯虚数
- 若 \(B\) 是 skew-Hermit \(\rightarrow\) \(iB\) 与 \(\displaystyle \frac{B}{i}\) 都是Hermit
- 若 \(A\) 是 Hermit \(\rightarrow\) \(iA\) 与 \(\displaystyle \frac{A}{i}\) 都是Skew-Hermit
- \(A\) 是 Hermit \(\Leftrightarrow\) \(iA\) 是 Skew-Hermit
正交阵
- \(A^TA=AA^T=I\)
- 性质
- 正交矩阵的任一行(列)同时乘以−1时,得到的新矩阵仍为正交矩阵
- 正交阵的所有特征值的模值为1
- 正交阵的行列式必为 \(\pm1\)
- 正交阵的乘积仍为正交阵
- 判定
- 定义法 \(A^TA=AA^T=I\)
- \(n\)阶实方阵\(A\)是正交矩阵当且仅当
- \(A\)的所有特征值的模值为\(1\)
- 且存在酉矩阵\(U\)使得 \(U^HAU=diag(λ_1,⋯,λ_n)\)
其中\(λ_1,⋯,λ_n\)是A的n个特征值
优阵(U阵)
- 如果 \(A=(\alpha_1,\alpha_2,\cdots,\alpha_n)_{n\times n}\) 是预优阵且\(|\alpha_1|=|\alpha_2|=\cdots=|\alpha_p|=1\),那么\(A\) 是一个优阵
- 判定
- \(A=(\alpha_1,\alpha_2,\cdots,\alpha_n)_{n\times n}\)是U阵 \(\iff\)
- \(|\alpha_1|=|\alpha_2|=\cdots=|\alpha_p|=1\)
- 且 \(\alpha_1\perp\alpha_2\perp\cdots\perp\alpha_n\)
- \(A=A^{n\times n} 是 U阵 \\ \Leftrightarrow A^{H} A=I_{\mathrm{n}} \\ \Leftrightarrow A^{-1}=A^{H} \\ \Leftrightarrow AA^{H}=I_{\mathrm{n}}\)
\(\because AA^{-1}=I\)
- 注意:U阵必可逆
- \(n\)阶复方阵\(A\)是U阵当且仅当
- \(A\)的所有特征值的模值为\(1\)
- 且存在酉矩阵\(U\)使得 \(U^HAU=diag(λ_1,⋯,λ_n)\)
其中\(λ_1,⋯,λ_n\)是A的n个特征值
- \(A=(\alpha_1,\alpha_2,\cdots,\alpha_n)_{n\times n}\)是U阵 \(\iff\)
- 性质
如果 A 是U阵
- 如果 \(A_{n,n}和B_{n,n}\) 是U阵 \(\Rightarrow\) \(AB\)是U阵
- \(A 是U,且X_1\bot X_2\cdots\bot X_p \Rightarrow\) \(AX_1\bot AX_2\cdots\bot AX_p\)
- \(k=\pm1,kA=(k\alpha_1,k\alpha_2,\cdots,k\alpha_n)\text{ 为优阵}\)
- \(B=(\beta_1,\beta_2,\cdots,\beta_n)\)为优阵,其中\(\beta\text{ 组为 }\alpha\text{ 组的重排}\)
- \(|Ax|^2=|x|^2\)
![]()
- \(x\bot y\Rightarrow Ax\bot Ay\)
![]()
- \((Ax,Ay)=(x,y)\)
- 拓展性质
- U阵的任一行(列)同时乘以模为1的任何数后,得到的新矩阵仍为U阵
- U阵的乘积仍为U阵
- \(A\) 所有特征值的模值为1,行列式的模值为1
正规阵
- 方阵 \(A\) 满足 \(A^HA=AA^H\)
正规阵必为方阵
- 判定
- H 阵 、斜H阵、正交阵、(包含实正交阵)都是正规阵
- 对角阵一定是正规阵
- 严格三角阵(非对角形)一定不是正规阵
- 实对称与实反对称阵都正规
- 复方阵 \(A\) 是正规矩阵 当且仅当 \(A\) 有 \(n\) 个特征向量构成\(\Bbb C^n\) 空间的一组标准正交基,且属于 \(A\)的不同特征值的特征向量正交
- 复方阵 \(A\) 是正规矩阵 当且仅当 \(A\) 酉相似于对角阵
- \(n\)阶方阵\(A\)正规的充分必要条件是它与一个具有互异的特征值且与\(A\)有相同的特征向量的矩阵\(B\)可交换(即\(AB=BA\))
- 若两个正规矩阵可交换,则它们的乘积也是正规矩阵
- proof
![]()
- proof
- 性质
- 若\(A\)正规,则\(kA+cI\)正规
- 若\(A\)正规,则\(A\)与\(A^H\)必有相同特征向量
- 即若\(A\)正规,且\(AX=cX\),则\(A^HX=\bar{c}X\)
- 若\(A\)正规,则\(Q^HAQ\)也正规,其中\(Q\)为U阵(\(QQ^H=I\))
正规阵的优相似必正规
- 若\(A\)正规,则任意多项式\(f(A)=λ_ 0 I+λ _1 A+λ _2 A ^2 +⋯+λ_nA^K\)也正规
多项正规定理——正规阵的多项式也正规
- 正规阵的奇异值为特征值的绝对值
- 易错
- × 若A是正规矩阵,则A的特征向量必两两正交
- 引理
- \(\text{若分块阵 }A=\begin{pmatrix}B&C\\0&D\end{pmatrix}\text{正规,则 }C=0\text{,且 }B,D\text{ 都正规,即 }A=\begin{pmatrix}B&0\\0&D\end{pmatrix}\)
度量矩阵
Gram Martrix
- 定义
- 设\(ϵ_1,⋯,ϵ_n\)是内积空间 \(V\) 中的一组基,称n阶矩阵A 为\(V\) 关于基 \(ϵ_1,⋯,ϵ_n\) 的度量矩阵
![]()
- 记为 \(G(ϵ_1,⋯,ϵ_n)\)
- 设\(ϵ_1,⋯,ϵ_n\)是内积空间 \(V\) 中的一组基,称n阶矩阵A 为\(V\) 关于基 \(ϵ_1,⋯,ϵ_n\) 的度量矩阵
- tips
- 内积空间中内积与度量矩阵是一一对应的
- \((x,y)=η^HA^Hξ\)
- 设 \(ϵ_1,⋯,ϵ_n\) 是内积空间V的一组基,则 \(∀x,y∈V\),有
![]()
- 设 \(ϵ_1,⋯,ϵ_n\) 是内积空间V的一组基,则 \(∀x,y∈V\),有
- 性质
设 \(G(ε_1,⋯,ε_n)\) 和\(G(ϵ_1,⋯,ϵ_n)\) 均为内积空间 \(V\) 的度量矩阵
- \(G(ε_1,⋯,ε_n)\) 和 \(G(ϵ_1,⋯,ϵ_n)\) 是正定Hermite矩阵
- \(G(ε_1,⋯,ε_n)\) 和 \(G(ϵ_1,⋯,ϵ_n)\) 合同
- 即存在非奇异矩阵(可逆矩阵) \(P\) 使得
- \(P^HG(ε_1,⋯,ε_n)P=G(ϵ_1,⋯,ϵ_n)\)
- \(P\) 是由基 \(ε_1,⋯,ε_n\) 到基\(ϵ_1,⋯,ϵ_n\) 的过渡矩阵
Householder矩阵
- 定义
- 设 \(w∈ℂ^n\) 是单位向量
- \(H(w)=I−2ww^H\)
- 性质
- \(\big(H(w)\big)^H=H(w)=\big(H(w)\big)^{−1}\)
- \(|H(w)|=−1\)
特征值 n-1个1, 1个 -1
- 设 \(x, y∈ℂ^n\) 且\(x≠y\),则存在单位向量 \(w\) 使得\(H(w)x=y\) 的充分必要条件是
- \(x^Hx=y^Hy\quad,x^Hy=y^Hx\)
- 此时可取 \(\displaystyle w=\frac{e^{iθ}(x−y)}{‖x−y‖}\)
其中θ为任一实数,实际求就取0
- 一定可以酉相似对角化
奇异矩阵
- \(|A|=0\)
- 没有逆矩阵
λ矩阵
定义
- 以 λ多项式 为元素的矩阵称为\(\lambda\)矩阵,记为A(λ)
- \(A(λ)=[a_{ij}(λ)]_{m×n}\)
\(a_{ij}(λ)∈P_n(λ)\)
- \(A(λ)=[a_{ij}(λ)]_{m×n}\)
λ矩阵的秩
- 矩阵\(A(λ)\)中非零子式的最高阶数r 定义为\(A(λ)\)的秩,记为rank(A(λ))=r
- 例子
![]()
λ矩阵相抵
- 定义
- 若\(\lambda\)矩阵\(A(\lambda)\)经过有限次初等变换化为\(B(\lambda)\),则称\(A(\lambda)\)与\(B(\lambda)\)相抵
- \(\lambda\)矩阵的初等变换
![]()
- \(\lambda\)矩阵的初等变换
- 即存在可逆阵 \(P(\lambda)\) 和 \(Q(\lambda)\),使得 \(A(\lambda ) = P(\lambda)B(\lambda)Q(\lambda)\)
- \(A(λ)≅B(λ)\)
- 若\(\lambda\)矩阵\(A(\lambda)\)经过有限次初等变换化为\(B(\lambda)\),则称\(A(\lambda)\)与\(B(\lambda)\)相抵
- 判定
- \(\lambda\)矩阵\(A(\lambda)\)与\(B(\lambda)\)相抵 的充要条件
- or 完全一致的不变因子
- 即Smith标准型相同
- or 具有相同的各阶行列式因子
- 行列式因子
注意:行列式因子的个数=\(\lambda\)矩阵的秩!
- 设 \(\lambda\) 矩阵 \(A(\lambda)\) 的秩为 \(r\),对于正整数 \(1\le k\le r\),\(A(\lambda)\) 的全部 \(k\) 阶子式的首1最大公因式称为 \(k\) 阶行列式因子,记作\(D_k(\lambda)\)
- 例子
![]()
- 行列式因子
- or 完全一致的初等因子,且 \(rank\big (A(λ)\big)=rank\big(B(λ)\big)\)
- or 完全一致的不变因子
- \(\lambda\)矩阵\(A(\lambda)\)与\(B(\lambda)\)相抵 的充要条件
- 性质
- \(\lambda\)矩阵相抵则其秩相同,反之则不然
- 相抵的\(\lambda\)矩阵具有相同的秩和相同的各阶行列式因子
- 复方阵A和B相似当且仅当它们的特征矩阵相抵
- 相似与相抵之间的关系
![]()
- 相似与相抵之间的关系
- 例子
λ矩阵的逆矩阵
- 定义
- 设 \(A(λ)\) 是 \(n\) 阶 \(λ\) 方阵,若存在 \(n\) 阶\(λ\)方阵\(B(λ)\)满足\(A(λ)B(λ)=B(λ)A(λ)=I\) 则称λ矩阵A(λ)是可逆的,并称B(λ)为A(λ)的逆矩阵,记作\(A(λ)^{−1}\)
- 判定
- \(\lambda\)方阵\(A(\lambda)\)可逆的充分必要条件是其行列式\(|A(λ)|\)为非零常数
![]()
- \(\lambda\)方阵\(A(\lambda)\)可逆的充分必要条件是其行列式\(|A(λ)|\)为非零常数
Smith标准形
- 定义
- 设 \(λ\) 矩阵 \(A(\lambda)\) 的秩为 \(r\)
- 此标准形为\(A(\lambda)\)的Smith标准形
![]()
- \(d_i(λ)\) 是首1多项式,且 \(d_i(λ)|d_{i+1}(λ)\)
- tips
- \(A(\lambda)\)不一定是方阵,故Smith标准形不一定是对角阵
- Smith标准形中不变因子与行列式因子之间的关系
- 重要
![]()
- 重要
- \(\lambda\)矩阵的Smith标准形是唯一的
- Frobenious定理
- 设 \(A∈ℂ^{n×n}\)
- 其特征矩阵 \(λI−A\) 的Smith标准形为 \(\rm diag(d_1(λ),…,d_n(λ))\)
- 则 \(A\) 的最小多项式\(m_A(λ)=d_n(λ)\)
- 注:\(\lambda I−A\)的初等因子的最小公倍式即为矩阵\(A\)的最小多项式\(m_A(\lambda)\)
- 例子
- 求Smith标准型
![]()
![]()
- 求初等因子、不变因子、Smith标准型
![]()
- 求Smith标准型
不变因子
- 定义
- 在\(\lambda\) 矩阵\(A(\lambda)\)的Smith标准形中
- \(d_1(λ),⋯,d_{r}(λ)\) 由 \(A(\lambda)\)唯一确定的,称为\(A(\lambda)\)的不变因子
- tips
- 初等变换不改变\(\lambda\)矩阵的不变因子
- 例子
初等因子
- 定义
- 例子
- 注:初等因子组可能存在相同的因子
![]()
- 注:初等因子组可能存在相同的因子
- tips
- 初等变换不改变\(A(\lambda)\)的初等因子
- 设\(\lambda\)矩阵\(A(\lambda)\)为对角块矩阵
即\(A(λ)=diag(A_1(λ),⋯,A_s(λ))\)
- 则 \(A_1(λ),⋯,A_s(λ)\) 初等因子的全体就是\(A(λ)\) 的全部初等因子
- 行列式\(|\lambda I-A|\) 等于全体初等因子的乘积
tips
- 数字矩阵是特殊的\(\lambda\)矩阵
- 复方阵A的特征矩阵 \(λI−A\) 是\(\lambda\)矩阵
- \(λI−A\) 总是满秩的
- 行列式\(|\lambda I-A|\) 等于全体初等因子的乘积
- 行列式\(|\lambda I-A|\) 等于n阶行列式因子
- λ方阵\(A(λ)\)可逆的充分必要条件是其行列式\(|A(λ)|\)为非零常数
- 在求λ矩阵的Smith标准形、不变因子或初等因子时
- 可先将λ矩阵作初等变换,使得变换后的矩阵为对角(块)矩阵
- 利用定理求出λ矩阵的初等因子,进而求出Smith标准形和不变因子
单纯阵
- 定义
- 1
![]()
- 2
![]()
- 1
- 性质
- 方阵A是单纯矩阵的充分必要条件
- or \(A\)的特征矩阵 \(λI−A\)的初等因子是一次的
- or \(A\)的特征矩阵 \(λI−A\) 的不变因子无重根
- 充分条件
- 若复方阵A的零化多项式 \(g(λ)\) 无重根,\(\Rightarrow\)则矩阵A是单纯矩阵
- 若复方阵是幂等阵,则一定可以对角化
- 方阵A是单纯矩阵的充分必要条件
幂零阵、幂等阵
幂零阵
- 定义
- \(A^k=0\),\(A \in \Bbb C^{n\times n}\)
- 性质
- A的全体特征根为0
- \(|A+I| =1\)
- proof
![]()
- proof
幂等阵
也称 \(A\) 为 投影矩阵
- 定义
- \(A∈ℂ^{n×n}\)
- \(A^2=A\)
- 性质
\(A\in \Bbb C^{n\times n}_r\) 为幂等阵
- \(A^H\),\(A^∗\) 和 \(I−A\)都是幂等矩阵
- A 为单纯阵且相似于对角阵\(\Lambda = \begin{bmatrix} I_r & 0 \\ 0 & 0 \end{bmatrix}\)
- \(\rm tr(A)=rank(A)\)
- 幂等阵的特征值只能是或者0或1,\(r\)个1,\(n-r\)个0
- proof
![]()
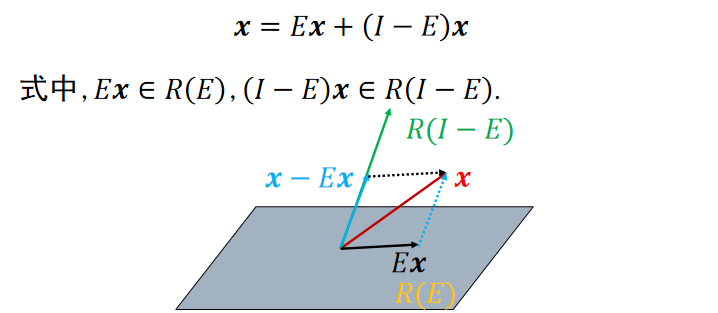
- \(N(A)=R(I-A)\)
充要条件
- \(\mathbb C^n=N(A) \dot{+}R(A)\)
- \(\mathbb C^n=N(A) \dot{+} N(A-I)\)
- \(Ax=x\) \(\iff\) \(x∈R(A)\)
其中 \(x\in \Bbb C^n\)
- proof
![]()
- proof
- \(\displaystyle \rm e^{tA}=I+(e^t-1)A\)
- 做题技巧
- 若\(A,B,A-B\)均为投影矩阵,则\(AB=BA=B\)
- proof 由\(A^2=A,B^2=B,(A-B)^2=A-B\\ \Rightarrow 2B =AB+BA\\ \Rightarrow2AB=AB+ABA,2BA=ABA+BA\\ \Rightarrow AB=BA=B\)
- 若\(A,B,A-B\)均为投影矩阵,则\(AB=BA=B\)
秩一矩阵
- \(A=\alpha \beta^T\),\(\rm rank(A)=1\)
- 性质
设\(A\) 为 \(n\) 阶 秩一矩阵
- \(A\) 的 \(n\) 个特征值是 1,1 个特征值为\(\rm tr(A)\)
- \(\rm tr(A) = \beta^T\alpha\)
- \(\rm tr(A) \neq0\) 时, \(A\) 可以相似对角化
- \(\rm A^k = tr(A)^{k-1} A\)
- \(\alpha\) 是 \(A\) 的 \(\rm tr(A)\) 特征值对应的的特征向量
- \(|\lambda I-A| = \lambda^{n-1}[\lambda-tr(A)]\)
- \(m_{\lambda}(A) = \lambda [\lambda-tr(A)]\)
- \(A\) 的非零奇异值为 \(\|\alpha\|_2 \|\beta\|_2\)
- \(\|A\|_2 = \|\alpha\|_2 \|\beta\|_2\)
矩阵的2范数即为最大奇异值
- \(\|A\|_F = \|\alpha\|_2 \|\beta\|_2\)
- 若\(B\)是秩为\(m\)的单纯矩阵,则\(B\)必可写成\(m\)个秩一矩阵之和
重要概念
共轭Conjugate
- 对复数 \(w=a+ib\)
- \(\overline{w}=\overline{a+bi}=a-bi\)
- 矩阵的共轭——矩阵内每个元素取共轭
- \(\overline{A}=(\overline{a_{i,j}})\)
- 性质
- 实矩阵
- \(\overline{A}=(\overline{a_{i,j}})=(a_{i,j})=A\)
- \(\text{对于任意 } A=A_{m\times n}\in\mathbb{C}^{m,n}, B=B_{m\times p}\in\mathbb{C}^{n,p}\)
- \(\overline{(AB)}=(\overline{A})(\overline{B})\quad\)
- 实矩阵
共轭转置=转置共轭
- \(A^H=\overline{A}^T=\overline{A^T}\)
- 性质
- \({(A^H)}^H=A\)
- \((A+B)^H=A^H+B^H\)
- \((kA)^H=\overline{k}(A^H)\)
\(k\in C\) (复数)
- \((ABC)^H=C^HB^HA^H\)
- \(\displaystyle (e^A)^H=e^{A^H}\)
矩阵的模/范数
- \(||A||=\sqrt{\sum|a_{i,j}|^{2}}\)
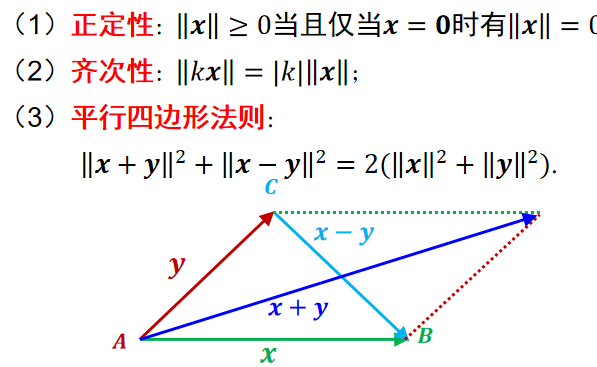
向量的模
- \(|| X||=\sqrt{(X,X)}=\sqrt{\left|x_1\right|^2+\left|x_2\right|^2+\cdots+\left|x_n\right|^2}\geq0\)
- 性质
\(∀x,y∈V\) 和 \(k∈F\)
迹
- \(tr(A)=a_{11}+\ldots+a_{nn}\)
- tips
- \(\rm tr(ABC)=tr(BCA)=tr(CAB)\)
- proof
![]()
- proof
- \(\rm tr(kA)=k\cdot tr(A)\)
- \(\rm tr(A+B)=tr(A)+tr(B)\)
- \(\displaystyle \frac {\partial tr(AB)}{\partial A}=\frac {\partial tr(BA)}{\partial A}=B^T\)
矩阵乘积的迹关于第一个矩阵的梯度等于第二个矩阵的转置
- proof
![]()
- proof
- \(\displaystyle \frac {\partial tr(A^TB)}{\partial A}=\frac {\partial tr(BA^T)}{\partial A}=B\)
- \(\rm tr(A) =\sum_i\lambda_i\)
矩阵的迹为所有特征值之和
- \(\rm tr(A)=tr(A^T)\)
- \(\rm tr(ABC)=tr(BCA)=tr(CAB)\)
模平方公式
- \(tr(A^{H}A)=tr(AA^H)=\sum|a_{i,j}|^{2}={||A||}_F^2\)
- \(\begin{aligned}tr(AA^{H})&=tr[(A^{H})^{H}A^{H}]\\&=||A^{H}||^{2}\\&=\sum|\overline{a_{ij}}|^{2}\\&=||A||_F^{2}\end{aligned}\)
- 推导前提——列向量的模平方公式
- 对于一个列向量\(X\)—— \(X^HX={\|X\|}^2\)
- \(\mathrm{tr}(X^HX)=\mathrm{tr}(XX^H)=\left|x_1\right|^2+\left|x_2\right|^2+\cdots+\left|x_n\right|^2=\sum\left|x_j\right|^2\overset{\text{记为}}{\operatorname*{=}}|\mathbf{X}|^2\)
- 推广公式
- 已知 \(A=(a_{ij})_{m\times n}、B=(b_{ij})_{m\times n} \in \Bbb C^{m\times n}\) 则
- \(tr(AB^H)=tr(B^HA)=\sum a_{ij}\overline{b_{ij}}\)
- \(tr(AB^T)=tr(B^TA)=\sum a_{i,j}b_{i,j}\)
- \(\mathrm{tr}(XY^{H})=\mathrm{tr}(Y^{H}X)=Y^{H}X=x_{1}\overline{y}_{1}+\cdots+x_{n}\overline{y}_{n}\)
\(\mathrm{~for~}X,Y\in\mathbb{C}^{\mathrm{n}}\)
- 已知 \(A=(a_{ij})_{m\times n}、B=(b_{ij})_{m\times n} \in \Bbb C^{m\times n}\) 则
全体特征根
- \(\lambda(A)=\{\lambda_1,\ldots,\lambda_n\}\)
特征值
- 设矩阵\(A∈ℂ^{n×n}\)的 \(n\) 个特征值为 \(λ_1,⋯,λ_n\)
- 则矩阵\(A^m\) 的n个特征值为 \(λ_1^m,⋯,λ_n^m\)
- 设矩阵\(A∈ℂ^{n×n}\)的 n 个特征值为\(λ_1,⋯,λ_n\),\(φ(λ)\)为任一多项式
- 则矩阵多项式\(φ(A)\)的n个特征值为\(φ(λ_1),⋯,φ(λ_n)\)
- 矩阵分析:特征值,相似度对角化,Jordan标准形_jordan标准型和特征值的关系-CSDN博客
- 补充性质
特征子空间
- 设\(\lambda\)是矩阵\(A\in \Bbb C^{n\times n}\)的一个特征值
- \(E(\lambda )=\{x∈\Bbb C^n|Ax=\lambda x\}\)
- \(E(\lambda )\)是\(\Bbb C^n\)的线性子空间,称为属于特征值\(\lambda\)的特征子空间
- \(\rm dim E(λ_i)=n−rank(\lambda_i I−A)\)为特征值\(\lambda_i\)的几何重数
- 代数重数
- 矩阵\(A\)的特征值\(λ_i\)作为特征方程根的重数,称为特征值\(\lambda_i\)的代数重数
- !!! 几何重数\(\leq\)代数重数
- 复方阵某一特征值的代数重数为1,则它的几何重数必为1
- 示例
![]()
- \(\rm dim(E(\lambda))\ge1\)
右逆、左逆
- A有右逆 的充要条件(即存在矩阵B使得\(AB= I\))
- A为行满秩矩阵
- A有左逆 的充要条件(即存在矩阵B使得\(BA= I\))
- A为列满秩矩阵
内积Inner product
定义在\(\Bbb C^n\)(列) 上的内积
\(X\)与\(Y\) 都是 \(C^n\) 上的列向量
- \(X\)与\(Y\)的标准内积
- \((X,Y)=Y^HX=\mathrm{tr}(XY^H)=x_1 \overline{y_1}+\cdots+x_n \overline{y_n}\)
\(X=\begin{pmatrix}x_{1}\\\vdots\\x_{n}\end{pmatrix}, Y=\begin{pmatrix}y_{1}\\\vdots\\y_{n}\end{pmatrix}\in\mathbf{C}^{n}\)
- \(YX^H=(Y,X)=\overline{(X,Y)}\)
- \((X,Y)=Y^HX=\mathrm{tr}(XY^H)=x_1 \overline{y_1}+\cdots+x_n \overline{y_n}\)
- 特例
- \((X,X)=\mathrm{tr}(XX^H)=X^HX=x_1\overline{x_1}+\cdots+x_n\overline{x_n}=\mid x_1\mid^2+\cdots+\mid x_n\mid^2=\mid X\mid^2\)
- 特性
- \(\mid X\mid^2=(X,X)=\mathrm{tr}(XX^H)=\mathrm{tr}(X^HX)=X^HX=\mid X\mid^2\)
- \(Y^HX=(X,Y) \\\) \(X^HY=(Y,X)=\overline{(X,Y)}\)
- \(\mid kX\mid=\mid k\parallel X\mid\\ \mid\frac{X}{k}\mid=\frac{\mid X\mid}{\mid k\mid},(k\neq0);\quad\\ \mid X\pm Y\mid\leq\mid X\mid+\mid Y\mid.\)
模长性质
- 如果 \(X \ne 0\) 则 \(\frac{X}{|X|}\) 是单位向量
单位化公式
- 内积性质
- \((X,X)\ge 0\)
- \((Y,X)=\overline{(X,Y)}\)
- \((kX,Y)=k(X,Y)\\ (X,kY)=\overline{k}(X,Y)\)
\(k\in C\)
- \((X+Y,W)=(X,W)+(Y,W),\\(W,X+Y)=(W,X)+(W,Y)\)
- \(| (X,Y) |^{2}\leq(X,X)(Y,Y)\\ \mathrm{i.e.} | (X,Y) |\leq| X |\cdot| Y|\)
定义在\(\Bbb C^{m\times n}\)(复矩阵空间)上的内积
- 定义
- \(\begin{aligned}(A,B)&\triangleq tr(B^HA)=tr(AB^H)=\sum a_{ij}\overline{b_{ij}} ,A,B\in C^{m,n}\\(A,A)&\triangleq tr(A^HA)=tr(AA^H)=\sum a_{ij}\overline{a_{ij}} =\sum|a_{ij} |^2\end{aligned}\)
- 特性
- \((A,A)=tr(AA^H)=\sum\Bigl|a_{ij}\Bigr|^2\geq0\)
- \((B,A)=\overline{(A,B)}\)
- \((kA,B)=k(A,B)\)
- \((A,kB)=\overline{k}(A,B), k\in\mathbb{C}\)
- \((A+B,D)=(A,D)+(B,D)\)
- \((D,A+B)=(D,A)+(D,B)\)
- 性质
- \(|(A,B)|^2\le(A,A)(B,B),\text{即}|(A,B)|\le\|A\|\cdot\|B\|\)
- 内积形式(列分块)
- \(\begin{aligned}A&=\begin{pmatrix}a_{11}&\cdots&a_{1p}\\\vdots&\ddots&\vdots\\a_{n1}&\cdots&a_{np}\end{pmatrix}\in C^{n\times p}\\&=(\alpha_1,\cdots,\alpha_p),\text{其中}\alpha_i\text{为}n\text{维列向量}(n\times1\text{阶矩阵})\end{aligned}\)
- \(\begin{aligned}A^{H}& =\begin{pmatrix}\overline{a_{11}}&&\cdots&&\overline{a_{n1}}\\\vdots&&\ddots&&\vdots\\\overline{a_{1p}}&&\cdots&&\overline{a_{np}}\end{pmatrix} \in C^{p\times n} \\&=\begin{pmatrix}\overline{\alpha_1}^T\\\vdots\\\overline{\alpha_p}^T\end{pmatrix}\text{,其中}\overline{\alpha_1}^T\text{是}n\text{维行向量}1\times n\text{阶矩阵}\end{aligned}\)
- \(\begin{aligned}A^{H}A& =\begin{pmatrix}\overline{\alpha_1}^T\\\vdots\\\overline{\alpha_p}^T\end{pmatrix}(\alpha_1,\cdots,\alpha_p) \\&=\begin{pmatrix}\overline{\alpha_1}^T\alpha_1&&\overline{\alpha_1}^T\alpha_2&&\cdots&\overline{\alpha_1}^T\alpha_p\\\overline{\alpha_2}^T\alpha_1&&\overline{\alpha_2}^T\alpha_2&&\cdots&\overline{\alpha_2}^T\alpha_p\\\vdots&&\vdots&&\ddots&\vdots\\\overline{\alpha_p}^T\alpha_1&&\overline{\alpha_p}^T\alpha_2&&\cdots&\overline{\alpha_p}^T\alpha_p\end{pmatrix} \\&=\begin{pmatrix}(\alpha_1,\alpha_1)&&(\alpha_2,\alpha_1)&&\cdots&&(\alpha_p,\alpha_1)\\(\alpha_1,\alpha_2)&&(\alpha_2,\alpha_2)&&\cdots&&(\alpha_p,\alpha_2)\\\vdots&&\vdots&&\ddots&&\vdots\\(\alpha_1,\alpha_p)&&(\alpha_2,\alpha_p)&&\cdots&&(\alpha_p,\alpha_p)\end{pmatrix} \\&=\begin{pmatrix}\overline{(\alpha_1,\alpha_1)}&&\overline{(\alpha_1,\alpha_2)}&&\cdots&&\overline{(\alpha_1,\alpha_p)}\\\overline{(\alpha_2,\alpha_1)}&&\overline{(\alpha_2,\alpha_2)}&&\cdots&&\overline{(\alpha_2,\alpha_p)}\\\vdots&&\vdots&&\ddots&&\vdots\\\overline{(\alpha_p,\alpha_1)}&&\frac{\vdots}{(\alpha_p,\alpha_2)}&&\cdots&&\overline{(\alpha_p,\alpha_p)}\end{pmatrix} \\&==\begin{pmatrix}|\alpha_1|^2&\overline{(\alpha_1,\alpha_2)}&\cdots&\overline{(\alpha_1,\alpha_p)}\\\overline{(\alpha_2,\alpha_1)}&|\alpha_2|^2&\cdots&\overline{(\alpha_2,\alpha_p)}\\\vdots&\vdots&\ddots&\vdots\\\overline{(\alpha_p,\alpha_1)}&\overline{(\alpha_p,\alpha_2)}&\cdots&|\alpha_\text{p}|^2\end{pmatrix}\end{aligned}\)
正交orthogonal
定义
- \(\begin{aligned}X\bot Y\iff(X,Y)=0& =x_1\overline{y_1} +x_2\overline{y_2} +\cdots+x_n\overline{y_n} \\&=\overline{\overline{x_1}\left.y_1\right.+\overline{x_2}\left.y_2\right.+\cdots+\overline{x_n}\left.y_n\right.} \\=(Y,X)\end{aligned}\)
\(X=\begin{pmatrix}x_{1}\\\vdots\\x_{n}\end{pmatrix}, Y=\begin{pmatrix}y_{1}\\\vdots\\y_{n}\end{pmatrix}\in\mathbf{C}^{n}\)
性质
- \(X\perp Y\iff\big(Y,X\big)=\overline{(X,Y)}=y_1\overline{x_1}+y_2\overline{x_2}+\cdots+y_n\overline{x_n}=0.\)
- \(X\perp Y\iff(Y,X)=0\iff(X,Y)=0\)
- \(X\perp Y\iff\mathrm{X}^HY=0\iff Y^HX=0\)
\(\mathrm{X}^{H}Y=(Y,X)=\overline{(X,Y)},\quad Y^{H}X=(X,Y)\)
- \(X\bot Y\Rightarrow aX\bot bY\)
\((aX,bY)=\overline{b}Y^HaX=a\overline{b}Y^HX=a\overline{b}(X,Y)=0\)
- \(X_1\perp X_2\perp\cdots\perp X_n \\ \Rightarrow|c_1X_1\pm c_2X_2 \pm\cdots\pm c_nX_n|^2 =|c_1X_1|^2+ |c_2X_2|^2+\cdots+|c_nX_n|^2\)
此时\(X_1,X_2,\cdots,X_n\)称为一个正交组
tips
- 零向量θ与任何向量均正交
- 正交向量组要求向量均为非零向量
- 正交向量组线性无关
- 向量 \(X\) 与 \(Y\) 正交当且仅当 \(‖X+Y‖^2=‖X‖^2+‖Y‖^2\)
勾股定理
- 在 \(n\) 维内积空间中,正交向量组中的向量个数不会超过n个
- 拓展
![]()
矩阵合同
- 若\(P^HAP=B(P可逆)\),则\(A\)与\(B\) 合同,记为 \(A\triangleq B\)
基本性质
- 对 称 性 : \(A\triangleq B\Longleftrightarrow B\triangleq A\)
- 传 递 性 : \(A\triangleq B, B\triangleq C\Longleftrightarrow A\triangleq C\)
矩阵相似
- 定义
- tips
- 两矩阵相似的充分必要条件是两矩阵的特征矩阵相抵
矩阵的秩
- 矩阵秩越乘越小:\(r(AB)<\rm min\{r(A),r(B)\}\)
- \(\rm r(A)=r(AB)\) 成立的充要条件是存在适当阶数的矩阵\(C\)使得\(ABC=A\)
- 一般的,若\(\rm (A-xI)(A-yI)=0\),则 \(A\) 可以对角化
- 例子 proof
![]()
- 例子 proof
- 对于任意 \(n\) 阶矩阵 \(A\),\(\rm rank(A^n)=rank(A^{n+1})\)
- 补充性质
- 一些结论
![]()
- 一些结论
零化多项式
定义
- 给定矩阵\(A∈ℂ^{n×n}\)
- 若存在多项式\(g(λ)\)使得\(g(A)=0\)
- 则称\(g(λ)\)为\(A\)的零化多项式
性质
- 复方阵A的零化多项式有无数个,A阵特征多项式的所有倍式都是A阵的零化多项式
首1多项式
- 对于一元多项式 \(g(λ)=a_nλ^n+a_{n−1}λ^n−1+⋯+a_1λ+a_0\)
- 如果 \(a_n≠0\),则称 \(a_nλ^n\)为多项式的首项
- \(n\) 称为 \(g(λ)\) 的次数,记为 \(deg\big(g(λ)\big)=n\)
- \(a_n\) 称为 \(g(λ)\) 的首项系数
- 若 \(a_n=1\),则称 \(g(λ)\) 为首1多项式
最小多项式
定义
- 复方阵 \(A\) 的零化多项式中最小次数的首1多项式称为矩阵A的最小多项式
- \(m_A(λ)\)
性质
- 矩阵A的最小多项式\(m_A(λ)\)是唯一的,且可整除矩阵A的任一零化多项式
- 特别的 \(m_A(λ) | f_A(λ)\)
- 矩阵A的特征多项式\(f_A(λ)\)与最小多项式\(m_A(λ)\)具有相同的根(不计重数)
- 矩阵A的最小多项式\(m_A(λ)\)必为特征多项式\(f_A(λ)\)的因式
- 例子
![]()
求法
- 利用Smith标准型求
- 利用特征多项式与定义求
- 利用Jordan标准型求
Jordan块
定义
- Jordan块
![]()
- Jordan标准形
![]()
- 例子
![]()
- 例子
- Jordan标准形定理
- 设矩阵\(J\)是复方阵\(A\)的Jordan标准形,则矩阵\(A\)与矩阵\(J\)相似
- 例子
- 题目
![]()
- 解答
![]()
![]()
- 题目
性质
- 任一Jordan块的最小多项式等于它的特征多项式,也是Jordan块所对应特征矩阵的初等因子
- 给定初等因子所作的最简\(\lambda\)矩阵就是Jordan块的特征矩阵
- Jordan块本身就是一个Jordan矩阵
- 对角阵是一个Jordan矩阵,它的每个Jordan块都是一阶的 \(\Leftrightarrow\) A 的初等因子都是一次的
- Jordan标准型中,不同Jordan块的对角线元素可能相同,故特征值\(\lambda_i\)的代数重数 \(\ge\) \(\lambda_i\) 对应的某个Jordan块的阶数
- 矩阵不一定可以相似对角化,但一定可以与Jordan矩阵相似
Jordan标准型求法
- ① 特征向量法
- 如果 \(\lambda_i\) 是 \(A\) 的单重特征值,则 \(\lambda_i\) 对应一阶Jordan块\(\rm J_1(\lambda_i)\)
- 如果 \(\lambda_i\) 是 \(A\) 的 \(r_i\) 重特征值(代数重数),设 \(\rm s_i=dim(E_{\lambda_i})\)
$E $ 指特征子空间,\(\rm dimE_{\lambda_i} = n-rank(A-\lambda_iI)\)等于\(\lambda_i\) 的几何重数
- 则对应 \(\lambda_i\) 有 \(\rm s_i\) 个 \(\lambda_i\)为对角元的Jordan块
- 且这些Jordan块的阶数之和等于 \(r_i\)
- 由\(A\)的所有相异特征值对应的Jordan块构成的Jordan矩阵即为\(A\)的Jordan标准型
- 例子
- ② 初等变换法
- 方法一
- 通过对\(\lambda I-A\)进行\(\lambda\)矩阵的初等变换得到Smith标准型
- 从而得到不变因子\(\Rightarrow\)初等因子\(\Rightarrow\)Jordan块
- 方法二
- 将\(\lambda I-A\)进行初等变换变成对角块矩阵
- 直接得到初等因子,从而得到Jordan块
- 方法一
- ③行列式因子法
- 通过定义求\(\lambda I-A\)的行列式因子
- 从而得到\(\Rightarrow\)不变因子\(\Rightarrow\)初等因子\(\Rightarrow\)Jordan块
Jordan分解方法
- 例子
Jordan标准型的幂
Jordan标准型求矩阵函数
- \(f(A) = P f(J)P^{-1}\)
tips
- 利用Jordan标准型求矩阵最小多项式的方法
- 单 Jordan 块情况
- 当 \(J\) 仅包含一个 Jordan 块 \(J_1\) 时,\(J_1\)的最小多项式 \(\rm m_{J_1}(\lambda)=(\lambda-\lambda_1)^{k_1}\)
- \(\lambda_1\)是 Jordan 块 \(J_1\) 的特征值
- \(k_1\)是 Jordan 块 \(J_1\) 的阶数
- 当 \(J\) 仅包含一个 Jordan 块 \(J_1\) 时,\(J_1\)的最小多项式 \(\rm m_{J_1}(\lambda)=(\lambda-\lambda_1)^{k_1}\)
- 当 J 包含两个 Jordan 块 \(J_1\) 和 \(J_2\)
- 矩阵 \(J\) 的最小多项式为\(\rm m_{J_1}(\lambda)=(\lambda-\lambda_1)^{k_1}\)和\(\rm m_{J_2}(\lambda)=(\lambda-\lambda_2)^{k_2}\)的最小公倍数
- 一般的Jordan标准型 \(J\)
- J 的最小多项式等于特征矩阵 \(\rm \lambda I-A\) 的初等因子的最小公倍数,恰为不变因子\(\rm d_n(\lambda)\)
- 例子
- 单 Jordan 块情况
- 引理
![]()
映射、变换
- 设 \(V\) 和 \(W\) 是两个非空集合,\(f\) 是 \(V\) 到 \(W\) 的一个映射
单射
- 对任意 \(x_1,x_2∈V\), 当 \(x_1≠x_2\) 时有 \(f(x_1)≠f(x_2)\)
满射
- 对任意 \(y∈W\) 都有一个元素 \(x∈V\) 使得 \(f(x)=y\)
即存在原像
双射
- \(f\) 既是单射,又是满射
即一一对应
变换
- 设 \(V\) 是一个非空集合,\(V\) 到自身的映射称为 \(V\)的变换
- V到自身的双射称为V的一一变换
- 若V是有限集,V的一一变换称为V的置换
线性映射、线性变换
- 定义
- 设 \(V\) 和 \(W\) 是数域 \(F\) 上的线性空间,如果映射 \(T:V→W\)满足下述性质,称 \(T\) 为 \(V\) 到 \(W\) 的一个线性映射
- 可加性:\(∀x,y∈V\) ,\(T(x+y)=T(x)+T(y)\)
- 齐次性:\(∀λ∈F\),\(T(λx)=λT(x)\)
- 特别的,当 \(V=W\) 时, 称 \(T\) 为 \(V\) 上的线性变换
- 特殊的线性变换1
定义映射 \(T:V→V\)
- 零变换:\(T(x)=θ, ∀x∈V\)
- 恒等变换:\(T(x)=x,∀x∈V\)
- 负变换:\(T(x)=− x,∀x∈V\)
- 特殊的线性变换2
定义 \(T:ℝ^2→ℝ^2,∀x=[x_1,x_2]^T∈ℝ^2\)
- 伸缩:\(T(x)=\bigg[ \begin{matrix} k_1 & 0 \\ 0 & k_2 \end{matrix} \bigg]x\)
\(k_1\) 和\(k_2\) 为正常数
- 反射:\(T(x)=(x_1,−x_2)\)
- 旋转:\(T(x) = \bigg[ \begin{matrix} cos\varphi & -sin\varphi \\sin\varphi & cos\varphi \end{matrix}\bigg]x\)
\(\varphi\) 为旋转角
- 伸缩:\(T(x)=\bigg[ \begin{matrix} k_1 & 0 \\ 0 & k_2 \end{matrix} \bigg]x\)
- 特殊的线性变换1
- 设 \(V\) 和 \(W\) 是数域 \(F\) 上的线性空间,如果映射 \(T:V→W\)满足下述性质,称 \(T\) 为 \(V\) 到 \(W\) 的一个线性映射
- 关于线性映射的tips
- 定理 设\(T\)是数域 \(F\)上线性空间 \(V\) 到 \(W\)的线性映射,若\(α_1,⋯,α_p\)是 \(V\) 的一组向量,\(k_1,\cdots,k_p \in F\)
- \(T(k_1α_1+⋯+k_pα_p)=k_1T(α_1)+⋯+k_pT(α_p)\)
- 推论 设\(T\)是数域 \(F\)上线性空间 \(V\) 到 \(W\)的线性映射
- \(T(θ)=θ^′, θ∈V,θ^′∈W\)
几何意义——线性映射必须保持原点不动,故解析几何中常见的平移变换一般不是线性变换
- \(T(−x)=−T(x),∀x∈V\)
- 若 \(α_1,⋯,α_p\) 是 \(V\) 中一组线性相关向量, 则\(T(α_1),⋯,T(α_p)\)是\(W\)中一组线性相关向量
- 若 \(T(α_1),⋯,T(α_p)\) 是 \(W\) 中一组线性无关向量,则 \(α_1,⋯,α_p\) 是 \(V\) 中一组线性无关向量
- \(T(θ)=θ^′, θ∈V,θ^′∈W\)
- 定理 设\(T\)是数域 \(F\)上 \(n\) 维线性空间 \(V\) 到 \(m\) 维\(W\)的线性映射
- 当且仅当 \(T\) 是单射时,\(V\)中线性无关向量组的像是\(W\)中线性无关向量组
- 当且仅当 \(T\) 是单射时,\(V\)中一组基的像是 \(W\) 中一组基。
此时映射 \(T\) 是双射
- 线性映射不一定将一组基映射为像空间的一组基
- 定理 设\(T\)是数域 \(F\)上线性空间 \(V\) 到 \(W\)的线性映射,若\(α_1,⋯,α_p\)是 \(V\) 的一组向量,\(k_1,\cdots,k_p \in F\)
- 关于线性变换的tips
设 \(T\) 是线性空间 \(V\) 的线性变换
- 若 \(T\) 可逆,则逆变换是线性变换
- 若 \(T\) 在欧式空间\(V\) 的一组标准正交基 \(x_1,\cdots,x_n\) 的矩阵是对称阵,则 \((T(x_i),x_j)=(x_i,T(x_j))\)
- 线性映射运算
- 线性映射的加法运算
- 设 \(T_1, T_2\in \mathcal L(V,W)\),定义 \(T_1\) 与 \(T_2\) 的和为\(\\\) \((T_1+T_2)(x)=T_1(x)+T_2(x)\),\(\forall x∈V\)
- 线性映射的数乘运算
- 设\(T\in \mathcal L(V,W),\lambda \in F\), 定义 \(λ\) 与 \(T\) 的数乘为\(\\\) \((\lambda T)( x)=\lambda\cdot T( x)\),\(\forall x∈V\)
- 线性映射的加法运算
- 线性映射空间、线性变换空间
- 集合 \(\mathcal L(V,W)\) 中赋以加法和数乘构成数域\(F\)上的线性空间,称为线性映射空间
- \(\mathcal{L}(V,W)\)表示线性空间V到W的所有线性映射的集合
- 特别地,\(\mathcal L(V)\)称为线性变换空间
- 注意:\(\rm dim(\mathcal L(V,W)) = \rm dim(V) \times \rm dim(W)\)
- 集合 \(\mathcal L(V,W)\) 中赋以加法和数乘构成数域\(F\)上的线性空间,称为线性映射空间
- 线性映射值空间和核空间
- 定义
- 设 \(T \in \mathcal L(V,W)\)
- 线性映射\(T\)的核空间 (零空间)
- \(N(T)=\{x∈V|T(x)=θ\}\)
- \(T\)的零度 (亏)
- \(\rm dim(N(T))\)
- 线性映射\(T\)的值空间(像空间)
- \(R(T)=\{y∈W|y=T(x),∀x∈V\}\)
- \(T\)的秩
- \(\rm dim(R(T))\)
- 性质
- 设\(V\)和\(W\)是数域\(F\)上的\(n\)维和\(m\)维线性空间,若\(T∈L(V,W)\)在\(V\)的基\(ε_1,⋯,ε_n\)和\(W\)的基\(η_1,⋯,η_m\)下的矩阵为\(A\)
- \(\rm dimN(T)= dimN(A)\)
- \(\rm dimR(T)=dimR(A)=rank(A)\)
- \(\rm dimN(A)+dimR(A)=n\)
- 设\(V\)和\(W\)是数域\(F\)上的\(n\)维和\(m\)维线性空间,若\(T∈L(V,W)\)在\(V\)的基\(ε_1,⋯,ε_n\)和\(W\)的基\(η_1,⋯,η_m\)下的矩阵为\(A\)
- 定义
- 正交投影变换
- 设 \(W\) 是线性空间 \(V\) 的非平凡子空间,定义 \(V\) 上的正交投影变换映射 \(T\)为
平凡子空间指零向量和自身
- \(T(x)=\mathrm{Proj_W}x\)
\(∀x∈V\)
- 若\(\alpha_1,\cdots,\alpha_p\) 为 \(W\) 的标准正交基
- \(T(x)=\mathrm{Proj_W}x\\=(x,\alpha_1)\alpha_1+(x,\alpha_2)\alpha_2+\cdots+(x,\alpha_p)\alpha_p\)
- 设 \(W\) 是线性空间 \(V\) 的非平凡子空间,定义 \(V\) 上的正交投影变换映射 \(T\)为
- 亏加秩定理
正交变换、酉变换
- 定义
- 若欧氏 (酉)空间中的线性变换 \(T\) 保持向量的内积不变
- \((T(x),T(y))=(x,y),∀x,y∈V\)
- 称 \(T\) 为正交(酉)变换
- 判定(充要条件)
设\(V\)是\(n\)维欧氏(酉)空间,\(T∈\mathcal L(V)\)
- \(T\)保持长度不变,即 \(\|T(x)\|=\|x\|\)
- 若 \(ξ_1,⋯,ξ_n\) 是\(V\) 中一组标准正交基,\(\\\) 则\(T(ξ_1),⋯,T(ξ_n)\) 也是\(V\) 中一组标准正交基
- \(T\)在\(V\)的任一标准正交基下的矩阵为正交(酉)矩阵
- 性质
- 正交变换保持两个向量的夹角不变
同构映射
- 定义
其实就是线性映射+双射
- 设\(V\)和\(W\)是数域\(F\)上的线性空间,\(\forall x,y\in V\), \(\forall λ\in F\)
- 存在双射 \(f:V→W\)满足
- (1)\(f(x+y)=f(x)+f(y)\)
- (2)\(f(\lambda x)=\lambda f(x)\)
- 则称线性空间\(V\)与\(W\)同构,\(f\)是\(V\)到\(W\)的同构映射
- 性质
设V和W是数域F上的线性空间,T: V→W是同构映射
- \(T(\theta) = \theta^{\prime}\),\(\theta\in V,\theta^{\prime}\in W\)
- \(T(-x)=-T(x)\),\(\forall x\in V\)
- \(T(\sum\alpha_ix_i) = \sum \alpha_iT(x_i)\),\(\forall \alpha_i\in F,\forall x_i\in V\)
- \(V\)的向量组 \(x_1,⋯,x_r\) 线性相关当且仅当其像\(T(x_1),⋯,T(x_r)\)线性相关
- 若 \(ε_1,⋯,ε_n\) 是\(V\)的一组基,则\(T(ε_1),⋯,T(ε_n)\)是\(W\)的一组基
- \(T\)的逆映射\(T^{−1}: W→V\)存在且是同构映射
- tips
- 线性空间同构当且仅当它们的维数相等
- 任一实(复)\(n\) 维线性空间均与 \(\Bbb R^n(\Bbb C^n)\) 同构
- 设\(V\)是数域 \(\Bbb R(\Bbb C)\)上的\(n\)维线性空间,则线性变换空间\(L(V)\)与 \(\Bbb R^{n\times n}\)(或 \(\Bbb C^{n\times n}\))同构
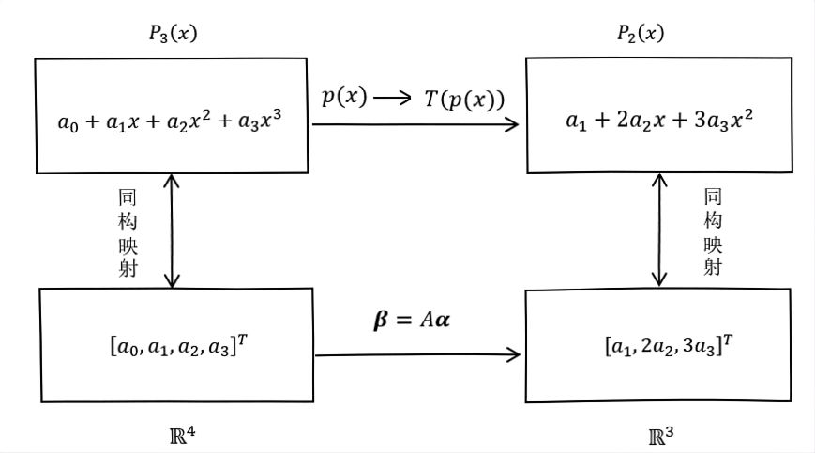
通过矩阵乘法实现线性映射
- 矩阵
- 线性映射与矩阵的关系
- 示例
![]()
- 示例
- 通过矩阵乘法实现线性映射
- 设 \(T\in \mathcal L(V,W)\),\(T\)在\(V\)的基\(ε_1,⋯,ε_n\)和\(W\)的基\(η_1,⋯,η_m\)下的矩阵为\(A\)。
- \(\Rightarrow\) \(T(ε_1,⋯,ε_n)\\ \triangleq[T(ε_1),⋯,T(ε_n)]\\=[η_1,⋯,η_m]A\)
- \(\forall x\in V\),设
- \(x=[ε_1,⋯,ε_n] \alpha\)
- \(T(x)=[η_1,⋯,η_m]\beta\)
- \(\Rightarrow\) \(\beta=A \alpha\)
- 设 \(T\in \mathcal L(V,W)\),\(T\)在\(V\)的基\(ε_1,⋯,ε_n\)和\(W\)的基\(η_1,⋯,η_m\)下的矩阵为\(A\)。
- tips
- 线性映射在不同基下的矩阵是相抵的
- 推论
- 相似矩阵反映的是同一个线性变换
![]()
- 相似矩阵反映的是同一个线性变换
重要公式、定理
许尔公式
- \(每个n 阶方阵\mathbf{A}=\mathbf{A}_{n\times n}\\ \text{都存在优阵 }\mathbf{Q}\\ \text{ 使得}\mathbf{Q}^{-1}\mathbf{A}\mathbf{Q}=\mathbf{D}=\begin{pmatrix}\lambda_1&\cdots&*\\&\ddots&\vdots\\0&&\lambda_n\end{pmatrix}\text{为上三角}\)
- Schur引理
酉相似三角化
- 任意复方阵\(A\)酉相似于上三角阵\(\Lambda\)
- 即存在U阵 \(U\) 使得 \(U^HAU=Λ\)
- \(U^HAU=Λ\)
- \(Λ\)——上三角矩阵
- \(U\)——U阵
- 实方阵Schur引理
- 设\(A∈ℝ^{n×n}\)的特征值均为实数,则存在正交矩阵 \(Q\) 使得
![]()
- 设\(A∈ℝ^{n×n}\)的特征值均为实数,则存在正交矩阵 \(Q\) 使得
- tips
- Schur引理表明任意复方阵都相似于上三角阵,但并不是所有复方阵都相似于对角阵
- 可酉相似对角化的矩阵
- 正规阵
- Hermite阵、反Hermite阵、正交阵、酉矩阵等都是正规阵
- Householder矩阵
- 正规阵
- 求Hermite矩阵\(A\)酉相似于对角阵的步骤
- 求出A的全部相异特征值及重数
- 对于每个特征值 \(λ\),求方程\((λI−A)x=0\)的一个基础解系,并将其单位正交化处理
- 由标准正交特征向量生成酉矩阵\(Q\),则\(Q^TAQ\)是对角矩阵
换位公式
特商公式
- \(\displaystyle\lambda=\frac{X^HAX}{|X|^2},\text{其中}(X\neq0\text{为}\lambda\text{的一个特征向量})\)
- \(\text{证明}:X^HAX=X^H\lambda X=\lambda X^HX=\lambda|X|^2(|X|^2>0)\)
平方公式
- 若 \(A\) 为半正定(\(A\ge 0\)),或 \(A\) 为正定(\(A>0\))
- 则有分解 \(A=B^2\),且 \(B^H=B\) 为 \(Hermite\) 半正定(\(B\ge0\))
- \(B\) 叫 \(A\) 的平方根,记作 \(\displaystyle B=\sqrt{A}=A^{\frac12}\)
秩公式
- \(r(AA^H)=r(A^HA)=r(A)\)
亏加秩定理
- 设T为数域F上的线性空间V到W的一个线性变换,即\(T \in \mathcal{L}(V,W)\)
- \(\rm dimN(T)+dimR(T)=dimV\)
- 即线性映射 \(T\) 的亏加秩等于其定义域 \(V\) 空间的维数
Cayley定理
- \(n\) 阶方阵的特征多项式 \(T(x)=|xI-A|\) 也是它的一个 零化多项式,\(\\\)即有 \(T(A)=0\)
- 由该定理得到的有趣性质
- 若\(A\in C^{n\times n}\),则\(A^n\)一定可以由\(A^{n-1},\cdots,A,I\)线性表示,其中\(n\geqslant2。\)
- 例题
Cauchy—Schwarz不等式
- 定义
- 设\(V\)是数域\(F\)上的内积空间,对 \(\forall x, y∈V\),有 \(|(x,y)|≤‖x‖‖y‖\)
- 注意:一般的线性空间不一定成立
- 其中等号成立当仅当 \(x, y\)线性相关
- 设\(V\)是数域\(F\)上的内积空间,对 \(\forall x, y∈V\),有 \(|(x,y)|≤‖x‖‖y‖\)
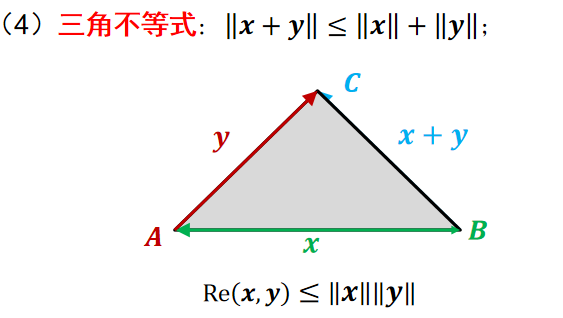
- 三角不等式
- 设 \(V\) 为欧式空间,则对任意的 \(\alpha,\beta\in V\),有
- \(|\alpha+\beta|\le |\alpha|+|\beta|\)
- 拓展
定义不同内积可得到不同的Cauchy不等式
- 对 \(ℝ^n\) 中任两向量 \(x=[x_1,⋯,x_n]^T\)和 \(y=[y_1,⋯,y_n]^T\)
- \(\displaystyle \left|\sum_{i=1}^nx_iy_i\right|\leq\sqrt{\sum_{i=1}^nx_i^2}\sqrt{\sum_{i=1}^ny_i^2}\)
- 对 \(ℝ^n\) 中任两向量 \(x=[x_1,⋯,x_n]^T\)和 \(y=[y_1,⋯,y_n]^T\)
Holder不等式
- \(\forall x=[x_1,x_2,\cdots,x_n]^T \in \Bbb C^n,y=[y_1,y_2,\cdots,y_n]^T \in \Bbb C^n\)
- 设 \(p,q>1\),且\(\displaystyle \frac1p + \frac1q=1\)
- \(\displaystyle \sum_{i=1}^n|x_iy_i|\le \bigg(\sum_{i=1}^n |x_i|^p\bigg)^{\frac1p}\bigg(\sum_{i=1}^n |y_i|^q\bigg)^{\frac1q}\)
Minkowski不等式
- \(\forall x=[x_1,x_2,\cdots,x_n]^T \in \Bbb C^n,y=[y_1,y_2,\cdots,y_n]^T \in \Bbb C^n\)
- \(p\ge1\)
- \(\displaystyle \bigg(\sum_{i=1}^n|x_i+y_i|^p \bigg)^{\frac1p}\le \bigg(\sum_{i=1}^n |x_i|^p\bigg)^{\frac1p}+\bigg(\sum_{i=1}^n |y_i|^p\bigg)^{\frac1p}\)

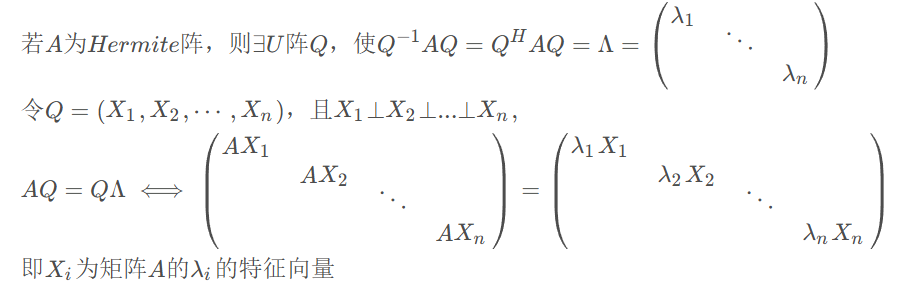


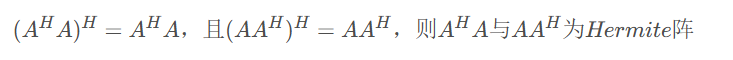
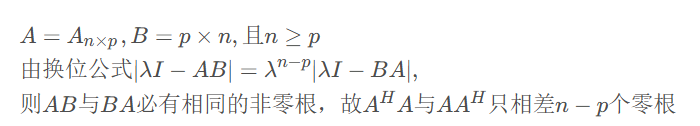


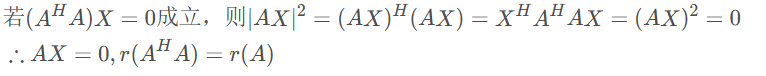





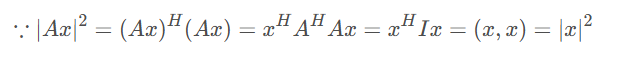
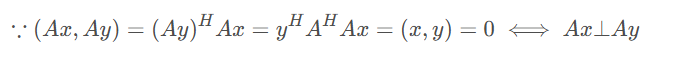

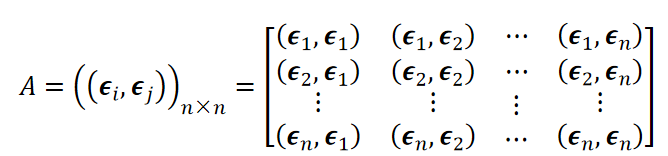
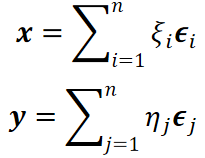
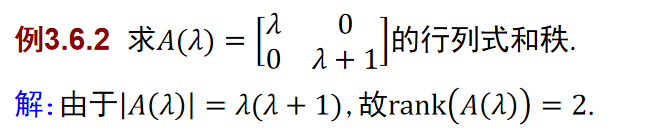





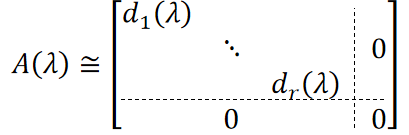


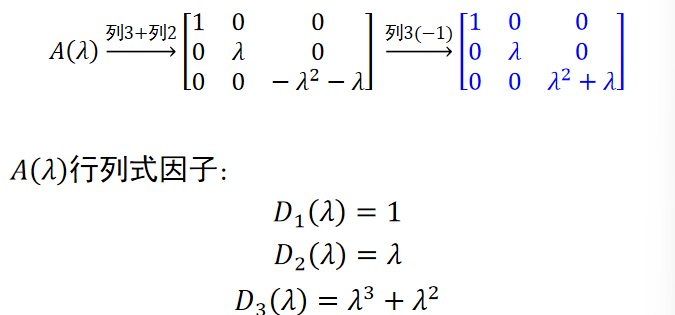

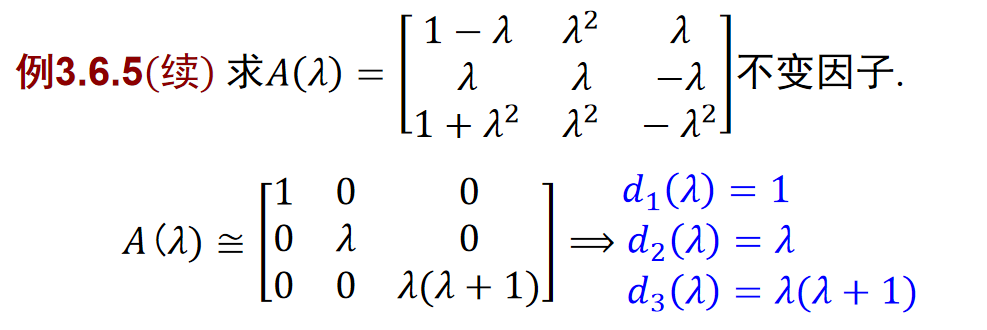












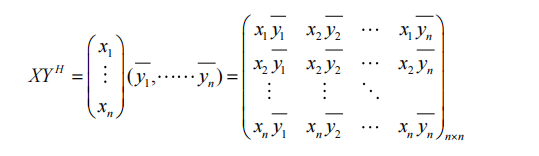
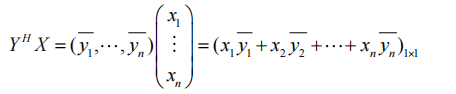





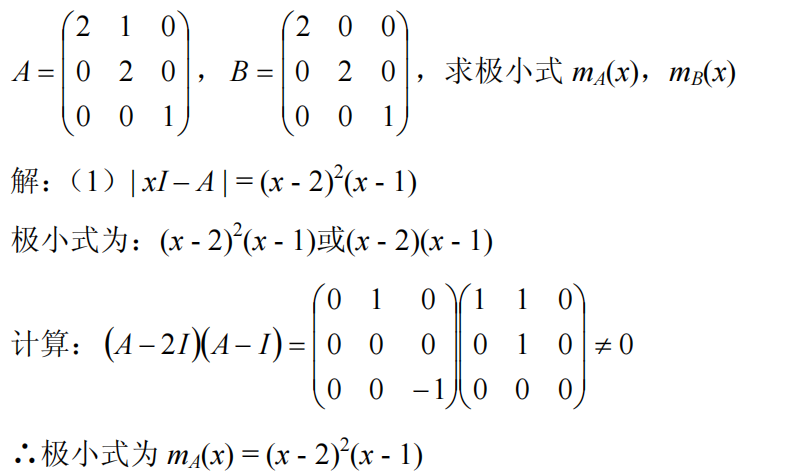



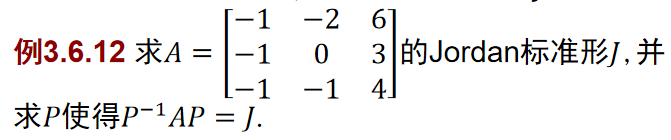





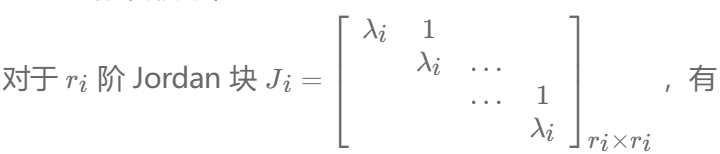
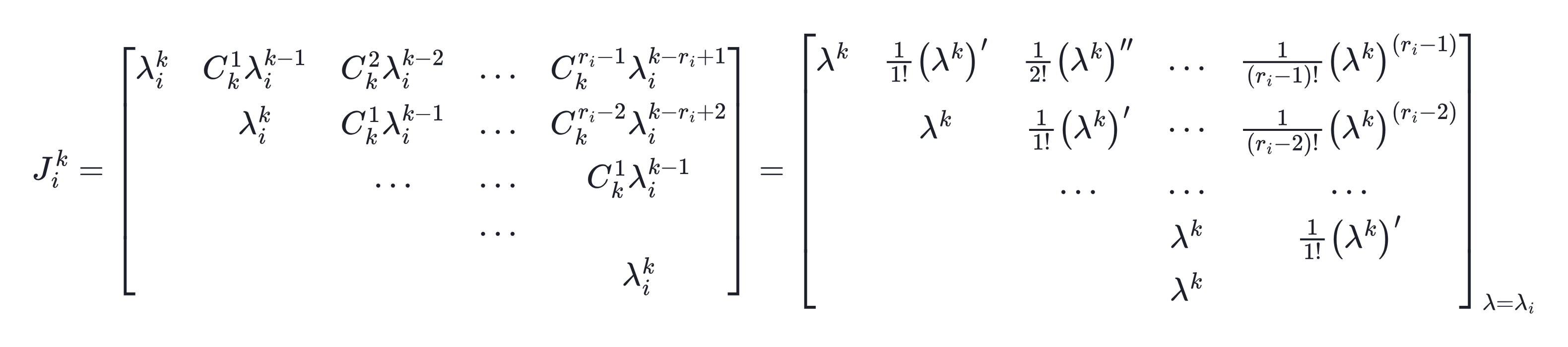





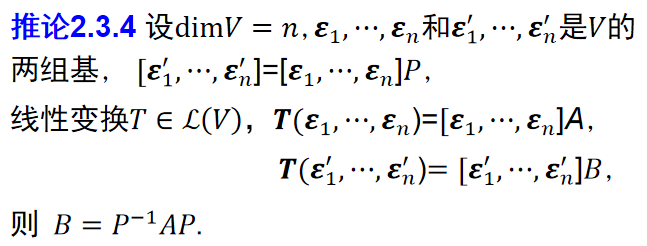
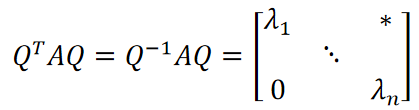
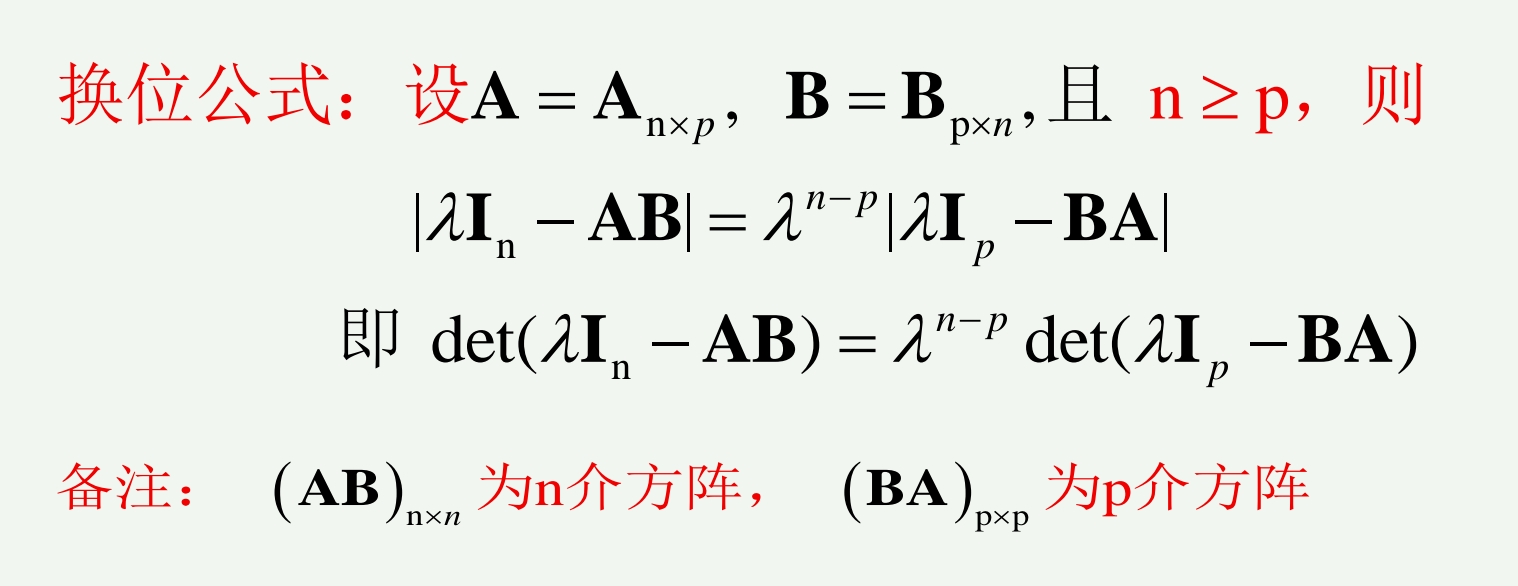

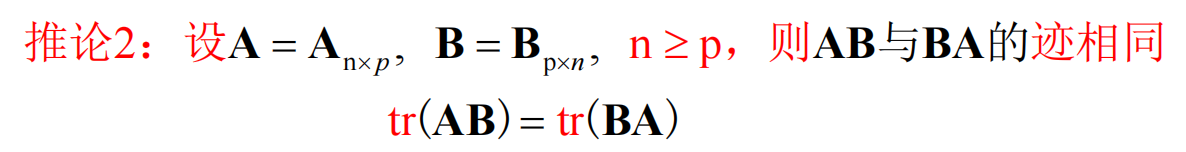
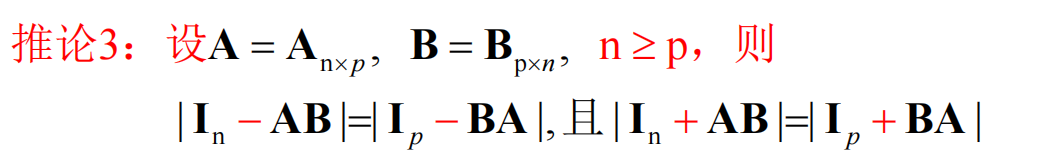


 浙公网安备 33010602011771号
浙公网安备 33010602011771号