01-2高等数学-导数

引例

导数的定义（变化率）

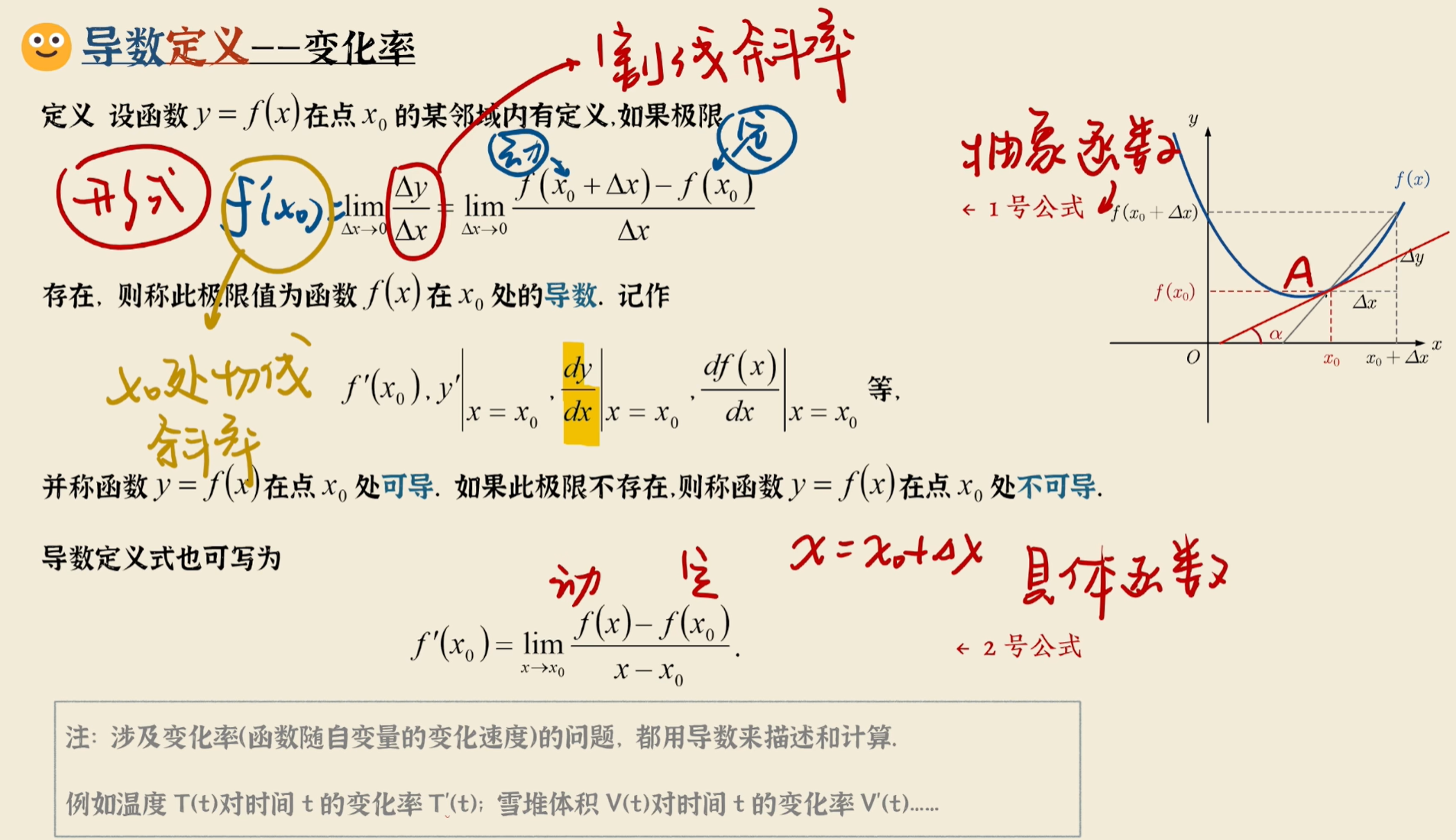
注：涉及变化率（函数随自变量的变化速度）的问题，都用导数来描述和计算。

导数的几何意义（切线、法线）

单侧导数

可导与连续

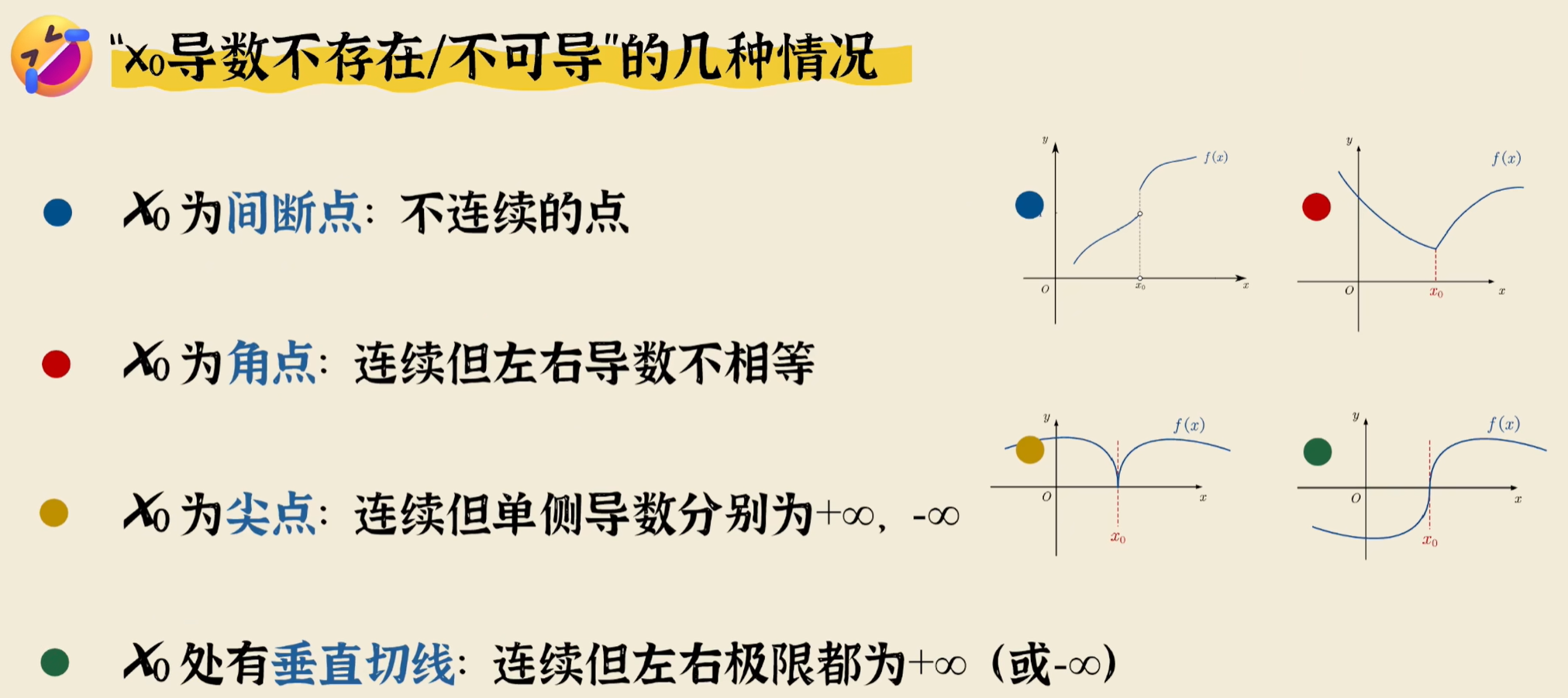
不可导的情况

导数公式--常数和基本初等函数

（不要死记硬背，现查现用）

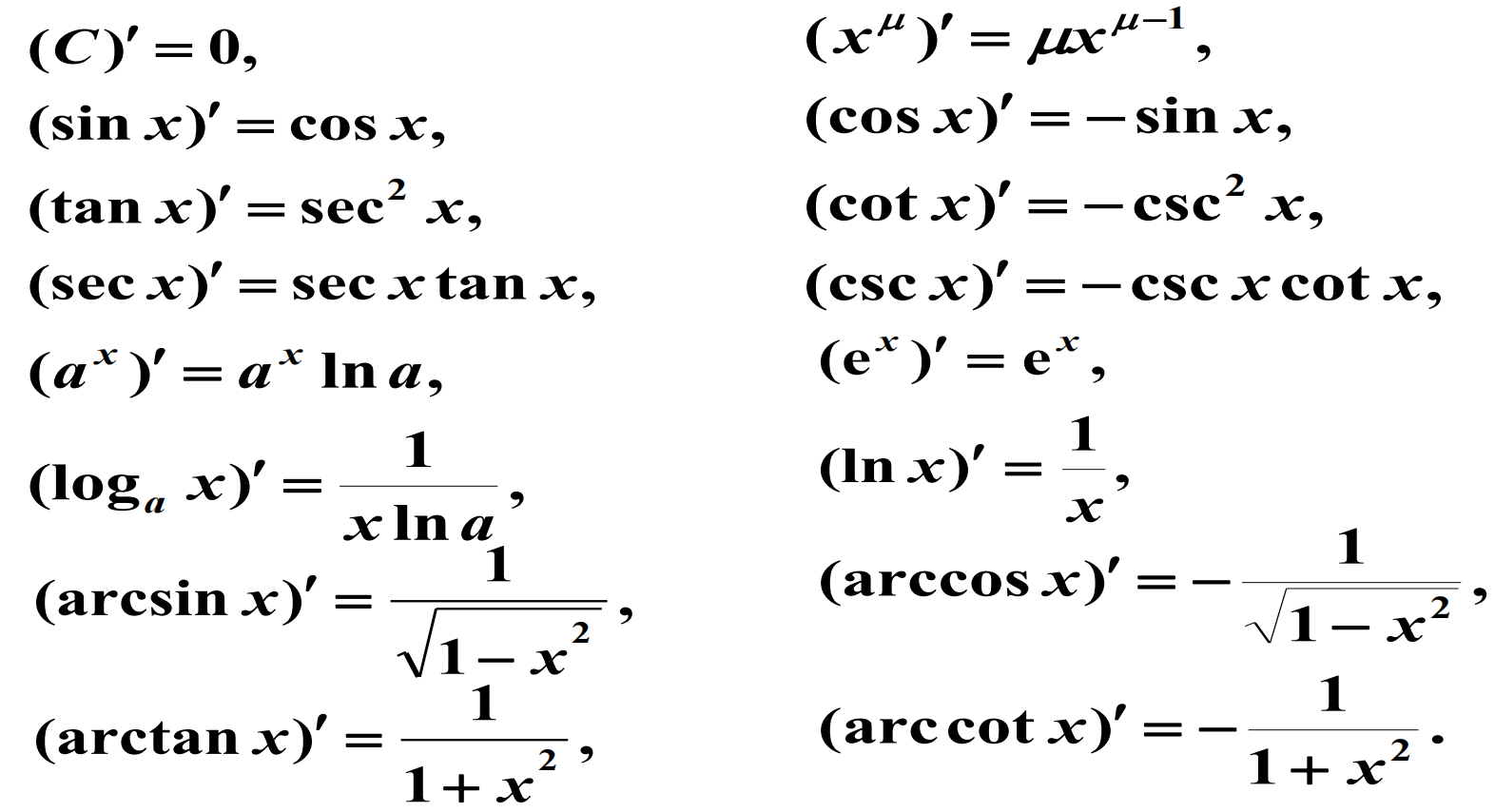
导数的运算（函数的和、差、积、商的求导法则）

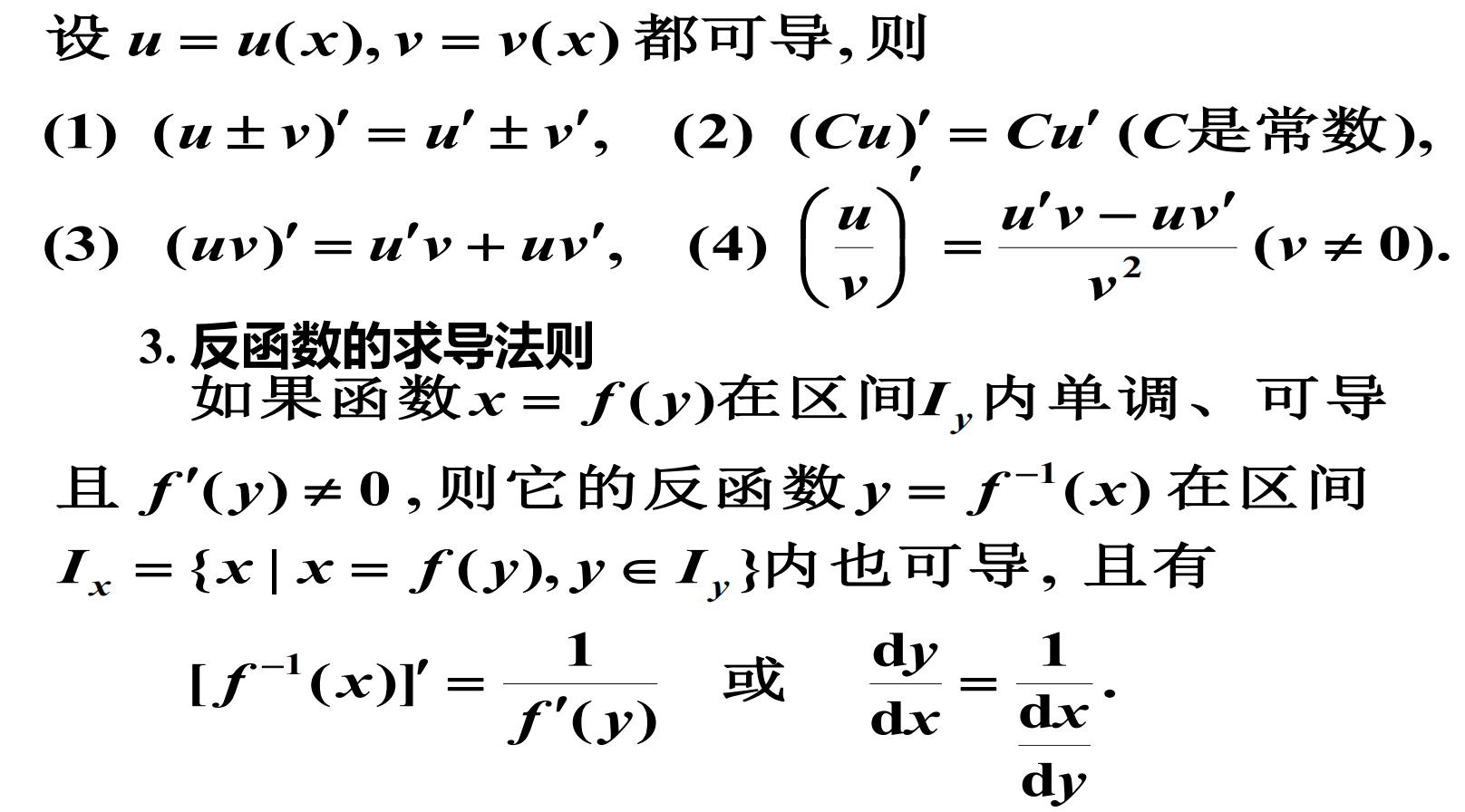
复合函数求导

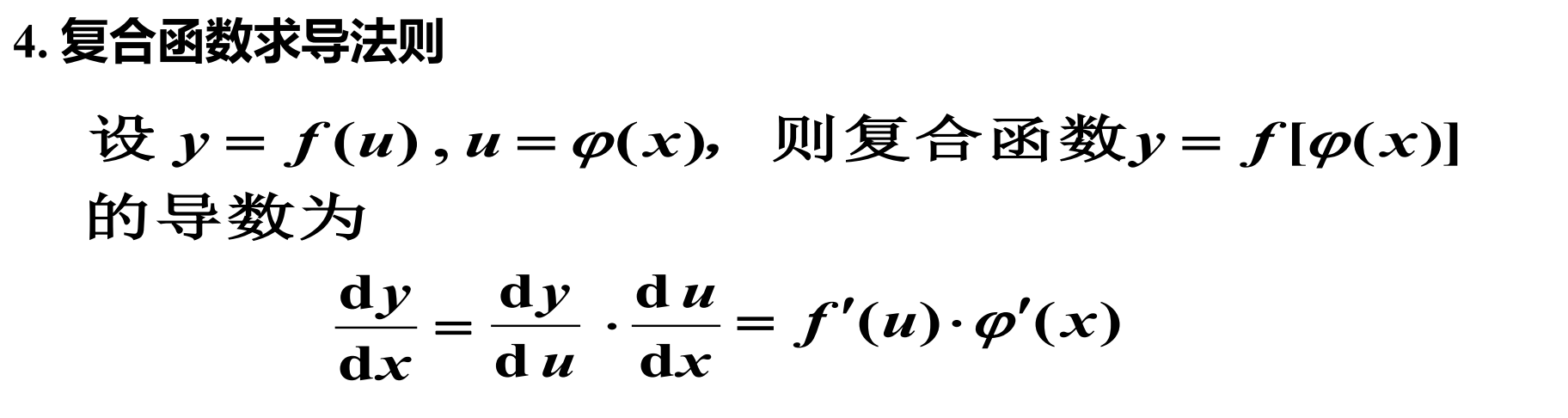
导数公式推导与案例解析

例：推导y=x²导数为什么等于2x

导数的运算例题

 

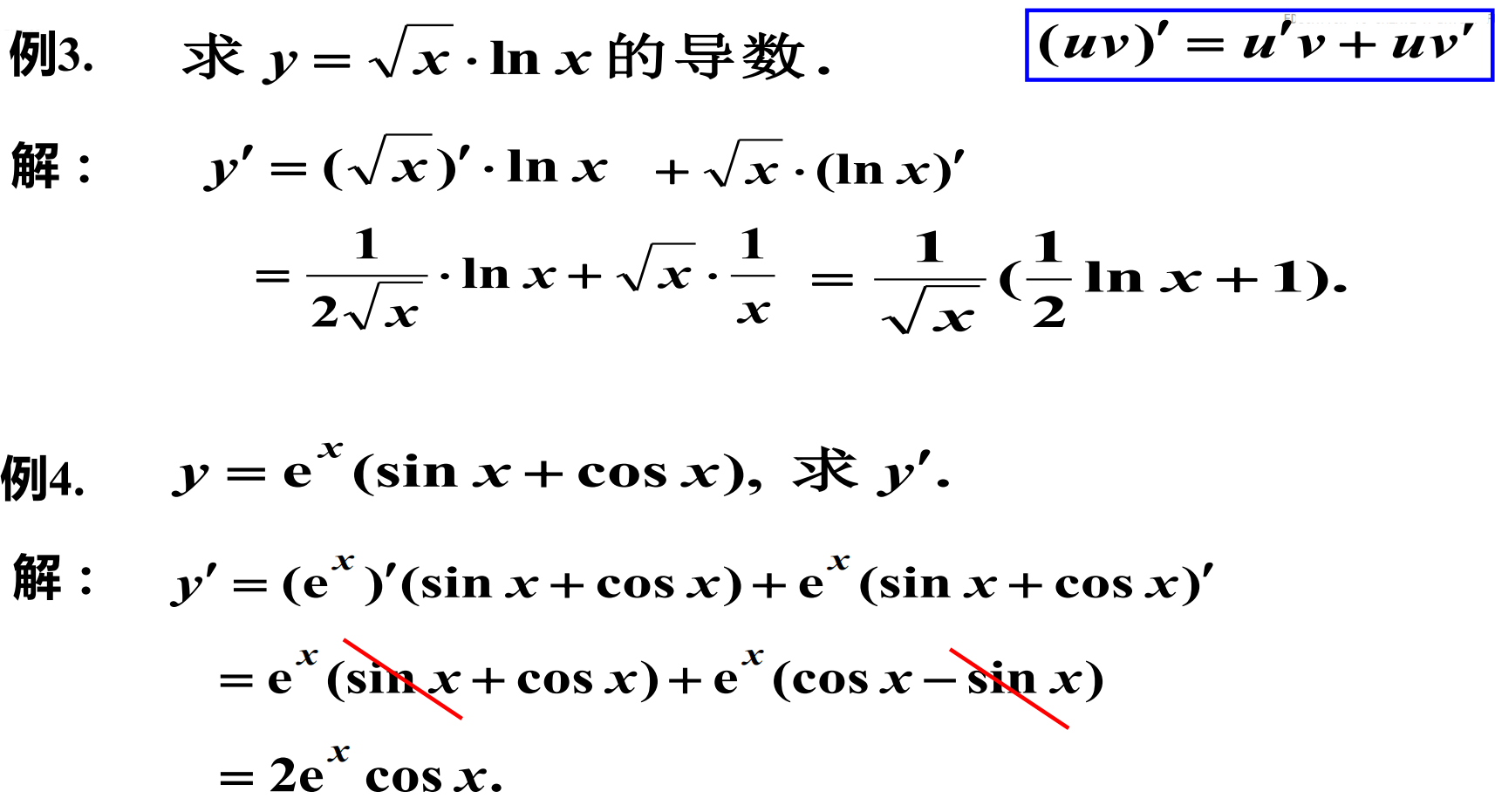
高阶导数

导数应用

1.判断函数单调性

通过函数的导数的值，可以判断出函数的单调性、驻点以及极值点：

在某一个区间内，若函数的导数大于0，则函数在这一个区间单调递增；若导数小于0，则单调递减；这种区间就叫做单调区间。

导数等于零的点为函数驻点。

驻点和不可导点处，函数可能取极大值或极小值(即极值可疑点)；

如果存在某点，使得该点之前区间上导数值都大于零，而之后的区间上导数都小于零，那么这个点就是一个极大值点，反之则是一个极小值点。

2.判断曲线的凹凸性

3.求函数的极值

注意！！！极值点并不一定是最值！！！

函数极值定义

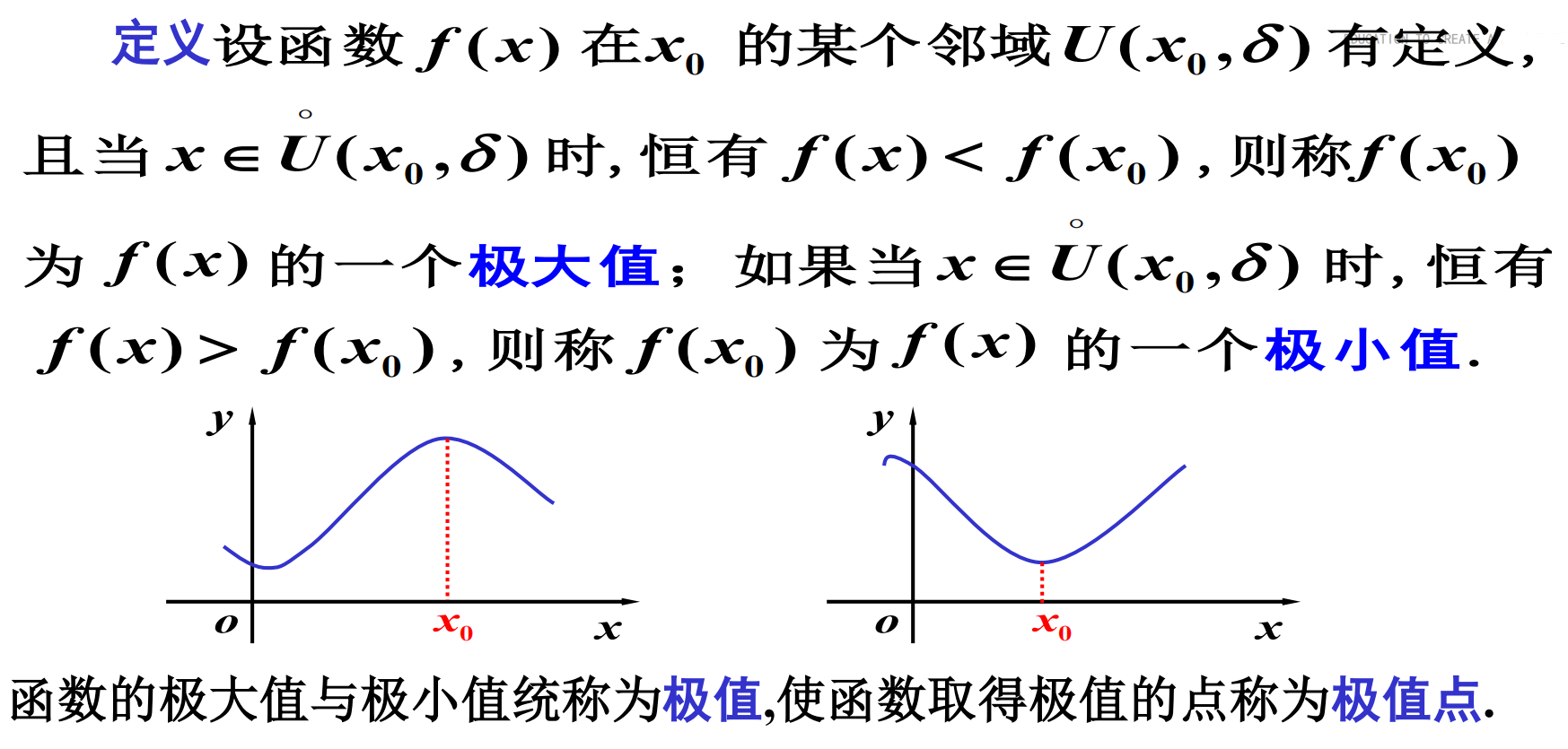
注：的意思是“去心”邻域（即不包含X₀，X0的左边δ范围和右边δ范围）；

若 f (x) 在极值点 x₀ 处可导，则 f ′(x₀ ) = 0 .

极值存在的第一充分条件：

极值存在的第二充分条件：

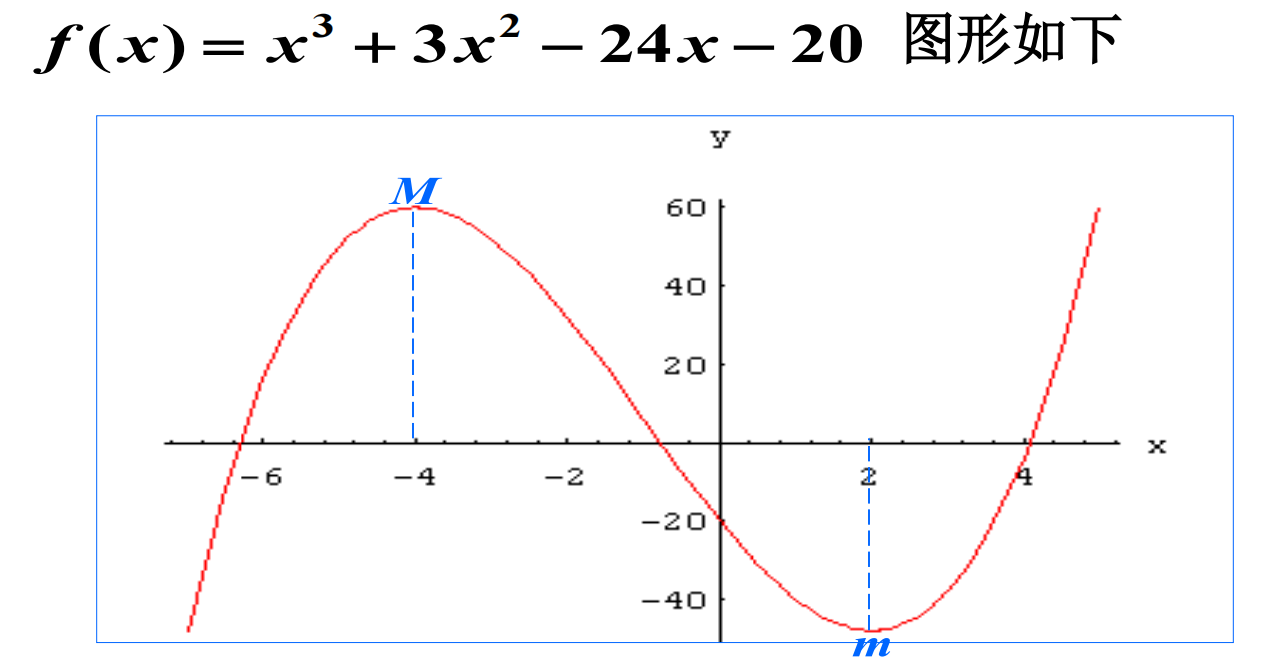
求极值的步骤总结:

(1) 确定函数的定义域；

(2) 求导数 f ′(x);

(3) 求定义域内部的极值嫌疑点(即驻点或一阶导数不存在的点)；

(4) 用极值的判定第一或第二充分条件。注意第二充分条件只能判定驻点的情形.

4.求函数最大值、最小值

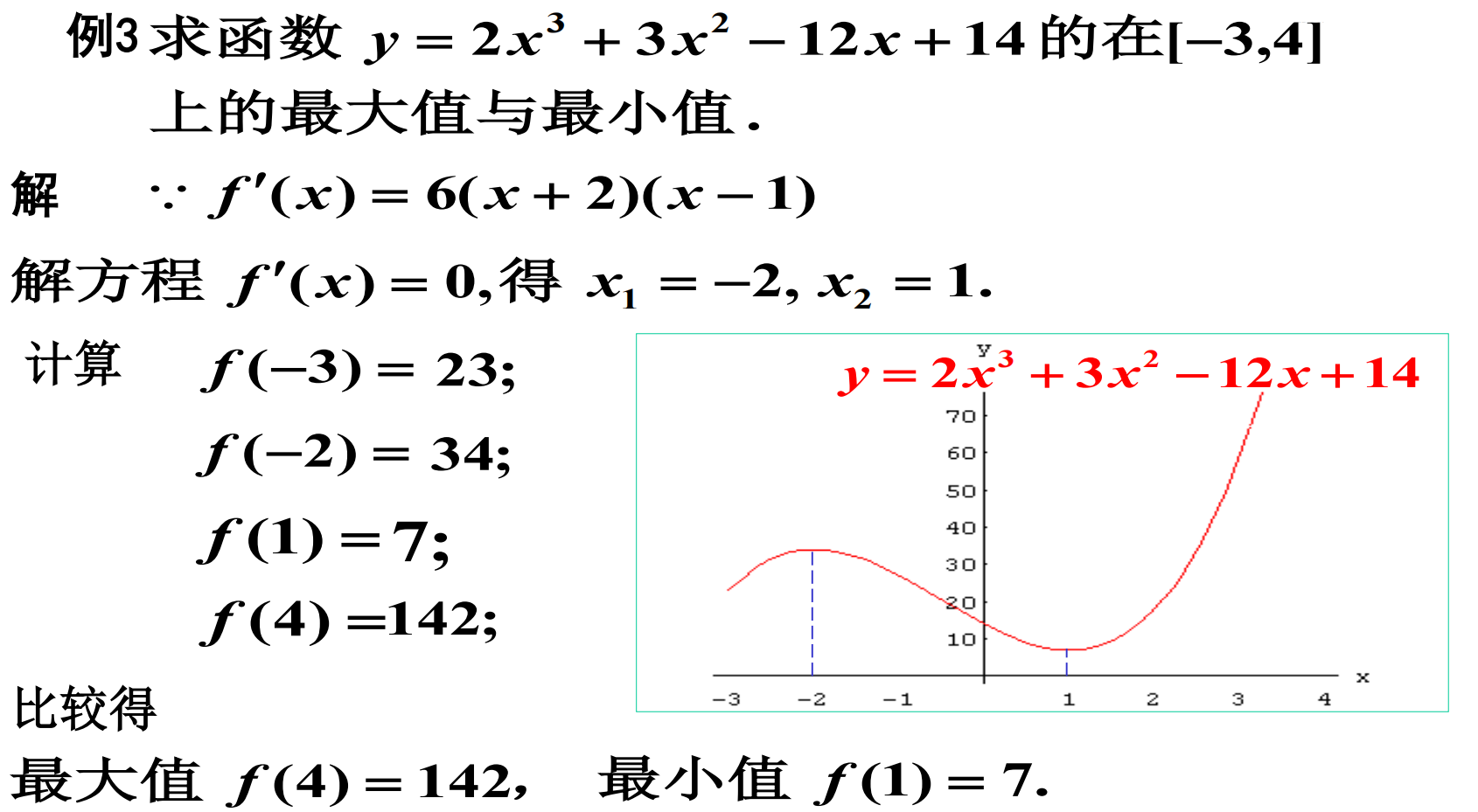
补充：

1）如果 f (x) 在[a,b] 上单调,则它的最值必在端点处取到；

2）如果 f ( x) 在[a,b]上连续,且在 (a, b) 内可导, 且有惟一驻点,则若为极小值点必为最小值点，若为极大值点必为最大值点；

  3）更进一步,若实际问题中有最大(小)值,且有惟一驻点,则不必判断极大还是极小,立即可以断定该驻点即为最大(小)值点.

最值例题：

• 正方形铁皮剪铁盒，如何剪面积最大

  将边长为a的正方形铁皮,四角各截去相同的小正方形,折成一 个无盖方盒,问如何截,使方盒的容积最大？为多少？

• 罐头盒如何用料最少

导数应用5 Taylor公式（泰勒公式）

详见下章：01-4高等数学-泰勒公式