01-4高等数学-泰勒公式
引言
假设y=10x,我们很容易计算出特殊点的值,例如x=1时y=10,x=2时,y=100。。。那么x=1.0001时,y=?我们是无法计算出来的。
同理,我们很容易算出sin(π/2)=1,但是sin(0.1)的值又怎么计算呢?
此时就要使用到泰勒公式来估计出近似值。
泰勒公式是什么
设函数 在点 处有 阶导数,则Taylor公式为:
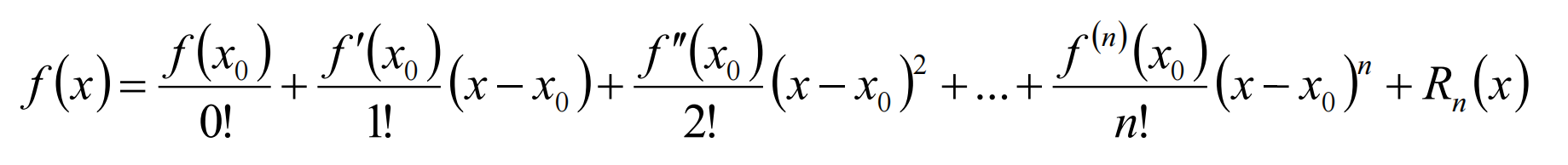
f(n) (x)表示f(x)的n阶导数
Rn (x)是Taylor公式的余项,是(x-x0 ) n的高阶无穷小
注:0!=1
Taylor公式又可写作:
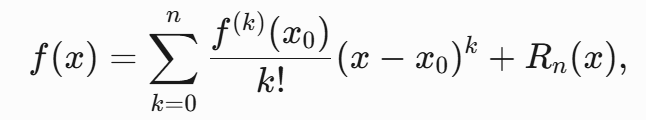


泰勒公式是用一个多项式来近似表示一个函数在某点附近的值。
泰勒公式是微积分中的核心工具。用简单的熟悉的多项式来近似代替复杂的函数。
其核心思想是通过函数的各阶导数信息,构造一个多项式来近似原函数,并估计误差。
Taylor(泰勒)公式是用一个函数在某点的信息描述其附近取值的公式。
如果函数足够平滑,在已知函数在某一点的各阶导数值的情况下,Taylor公式可以利用这些导数值来做系数构建一个多项式,近似函数在这一点的邻域中的值。
诞生背景

泰勒公式推导过程

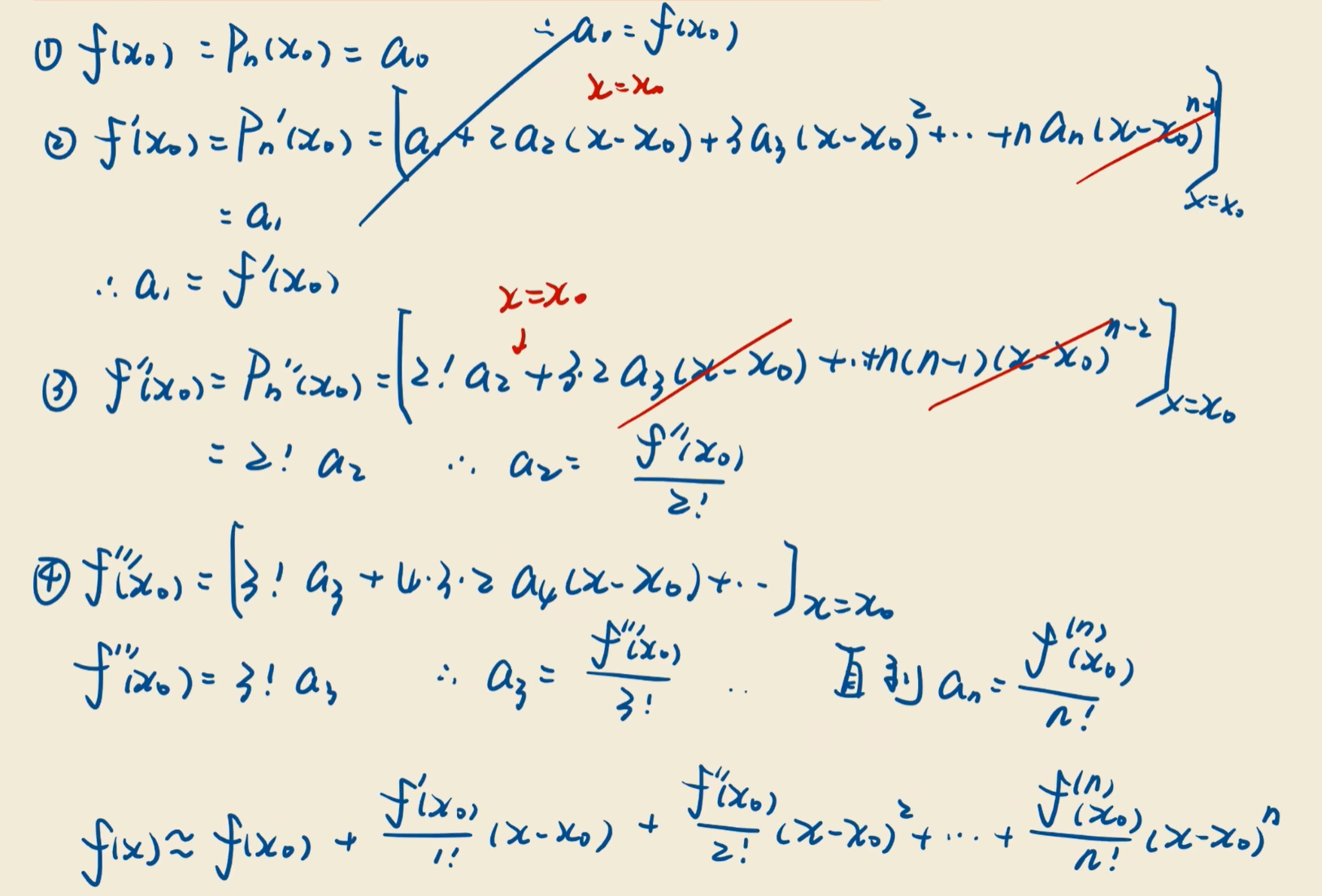
泰勒公式证明(了解):

泰勒公式的理解
1. :展开点(Center Point)
- 定义:泰勒公式的展开点是函数 被多项式近似的位置,即在该点附近展开函数。
- 作用:
- 所有导数 在 处计算。
- 多项式中的每一项均以 的形式表示与展开点的距离。
- 示例:
- 若 ,泰勒公式变为麦克劳林展开式(见下文)。
- 若 ,则多项式围绕 展开。
2. :目标点(Evaluation Point)
- 定义: 是需要用泰勒多项式近似计算函数值的位置。
- 关键条件: 必须在展开点 附近,且满足收敛条件(如 , 为收敛半径)。
- 示例:
- 若 ,泰勒多项式可近似计算 或 处的函数值。
- 若 离 太远,近似误差可能显著增大。
3. 泰勒公式的通用形式和余项
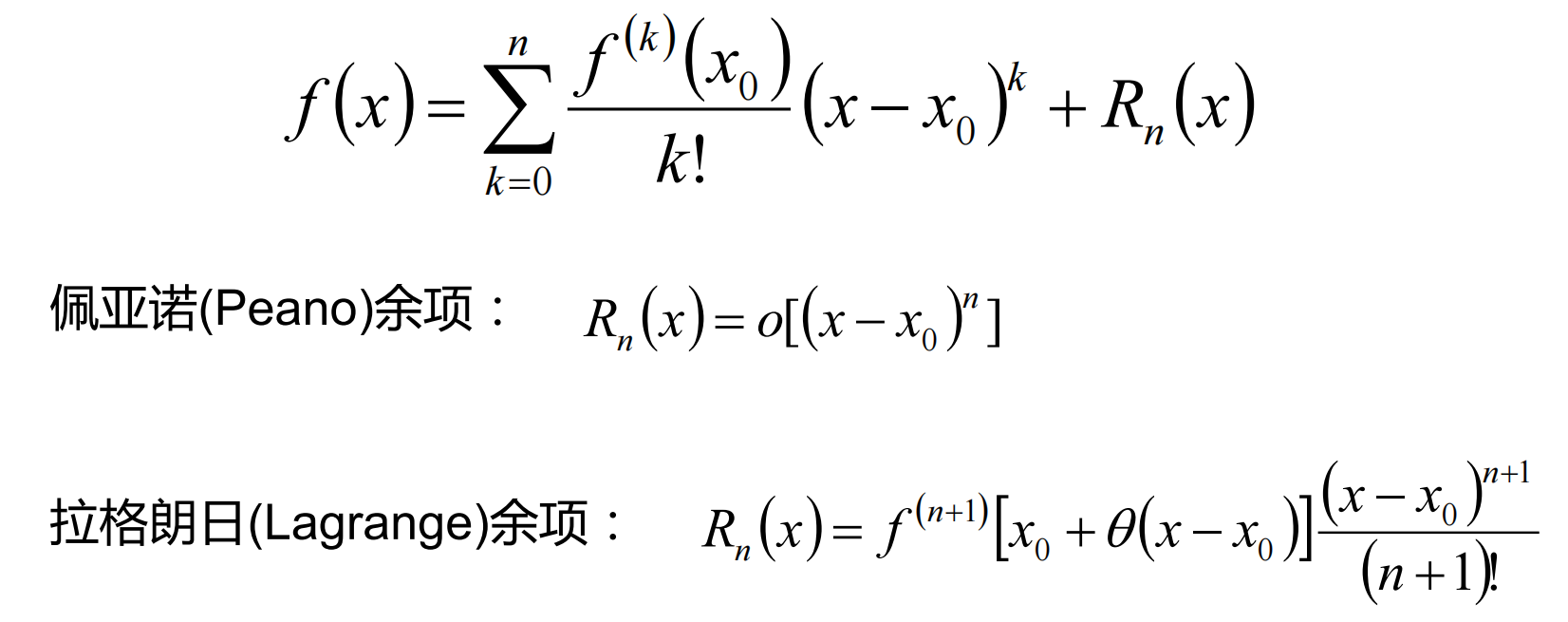
其中:
- :函数在 处的 阶导数。
- :目标点与展开点的距离的高次幂。
- :余项,表示多项式近似与真实值的误差。
4. 与 的关系
-
几何意义:
- 泰勒多项式是函数 在 处的“局部近似”,其精度在 附近最高。
- 随着 增大,余项 可能迅速增大。
-
收敛性:
- 泰勒级数的收敛半径 决定了 的有效范围。例如:
- 对于 (收敛半径 ),任何 均适用。
- 对于 (收敛半径 ),需满足 。
- 泰勒级数的收敛半径 决定了 的有效范围。例如:
-
实际应用:
- 选择 的策略:
- 若需近似 处的函数值,通常选择 以简化计算(此时余项为 0)。
- 若无法直接计算 ,则选择最接近 的已知点 。
- 选择 的策略:
总结
- :展开点,决定多项式在何处展开。
- :目标点,需在 附近以保证近似精度。
- 核心关系:泰勒多项式通过 的加权和,在 附近逼近 。选择合适的 是平衡计算复杂度和精度的关键。

麦克劳林公式(特殊 Taylor公式,x0=0)
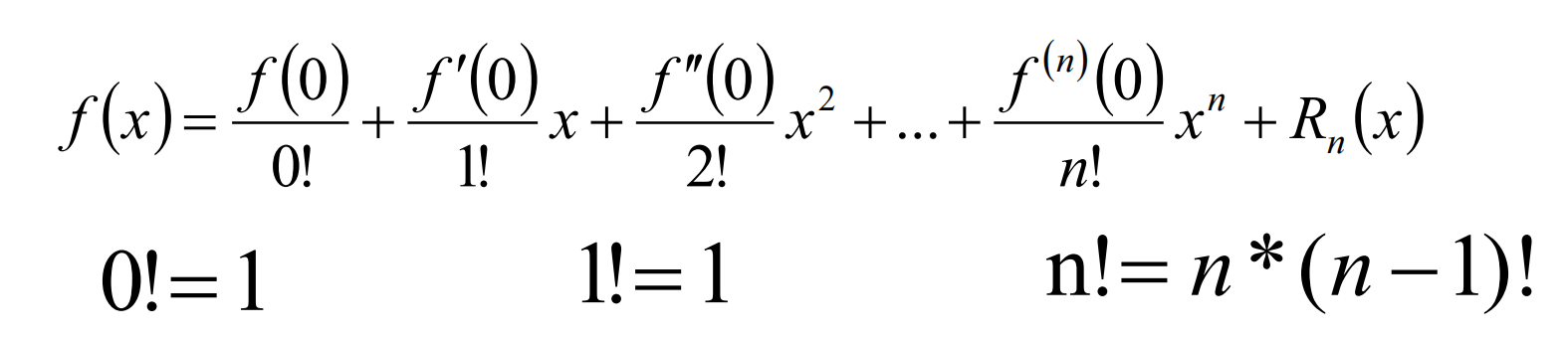
常用麦克劳林公式
几个常见的初等函数的带有佩亚诺余项的麦克劳林公式:

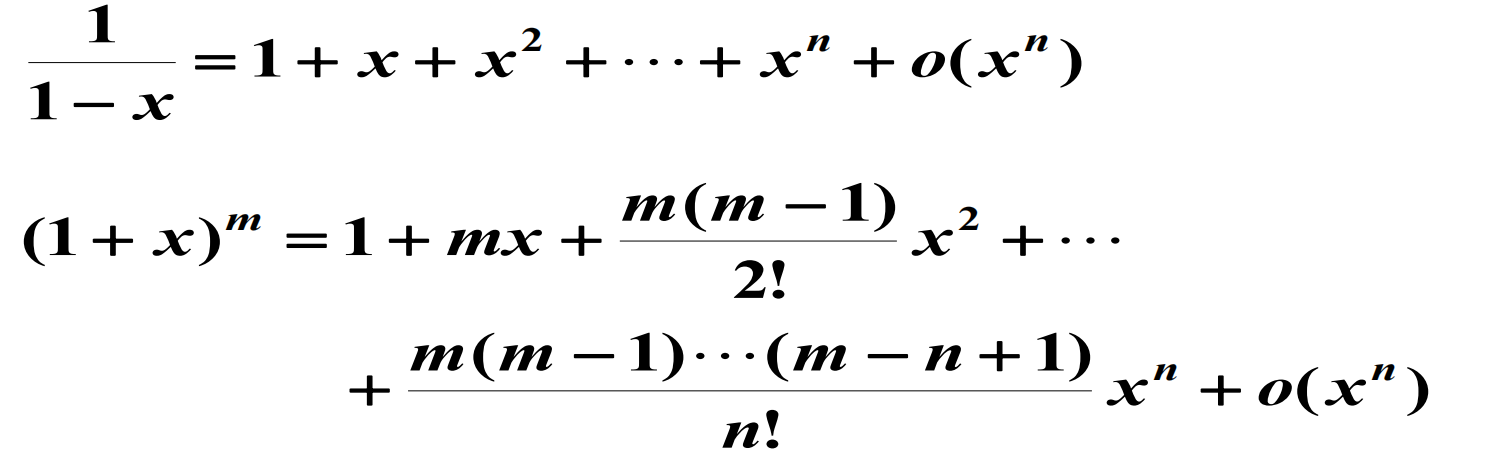
Taylor公式应用
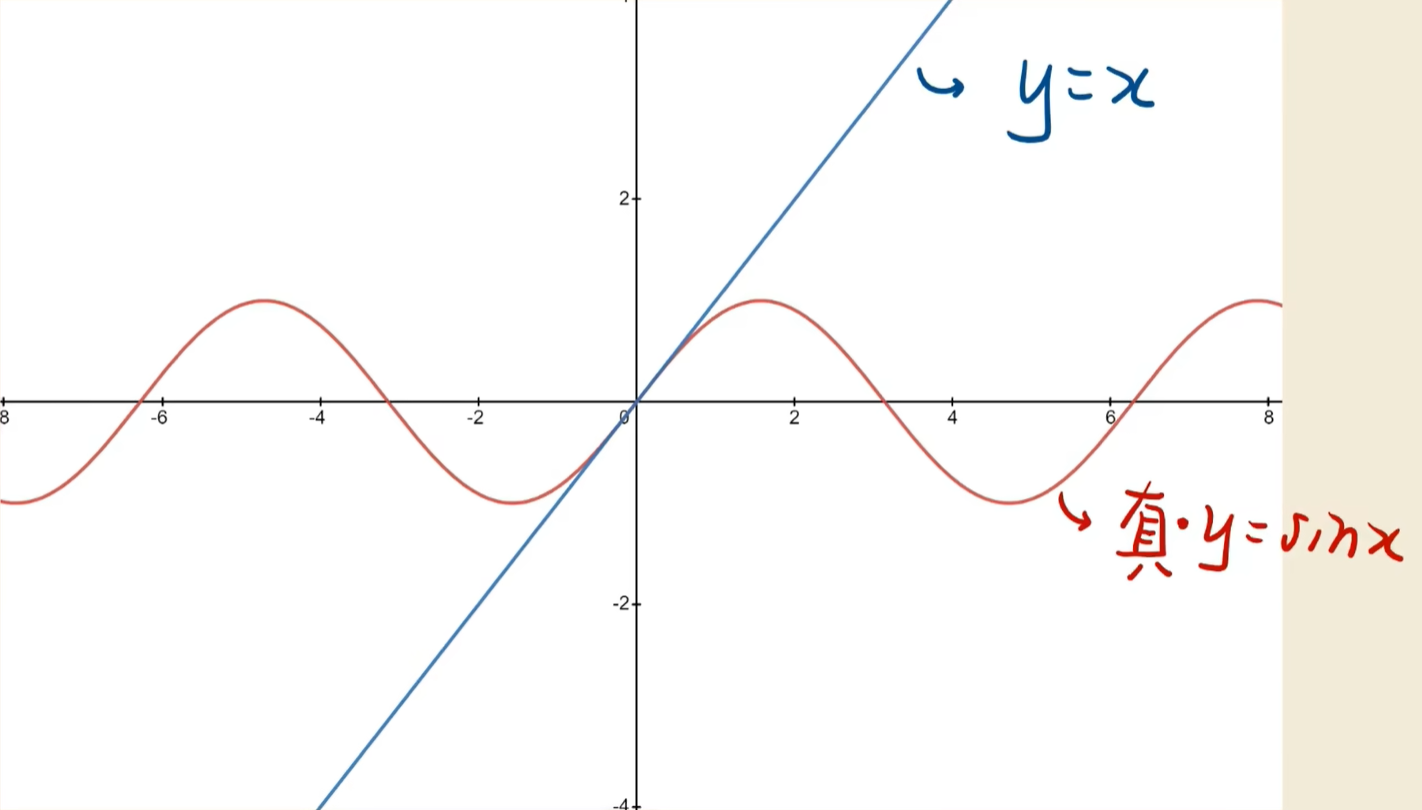
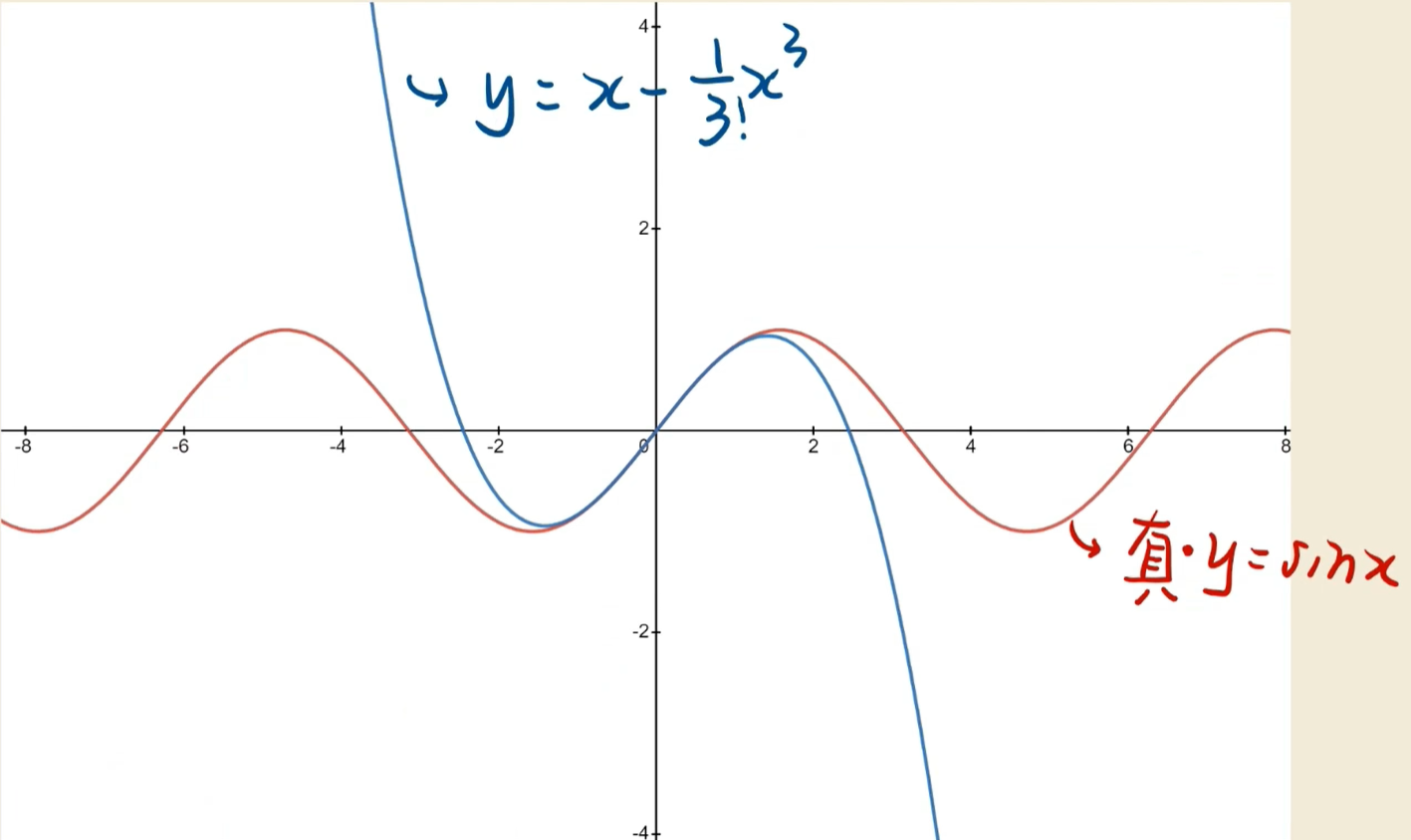
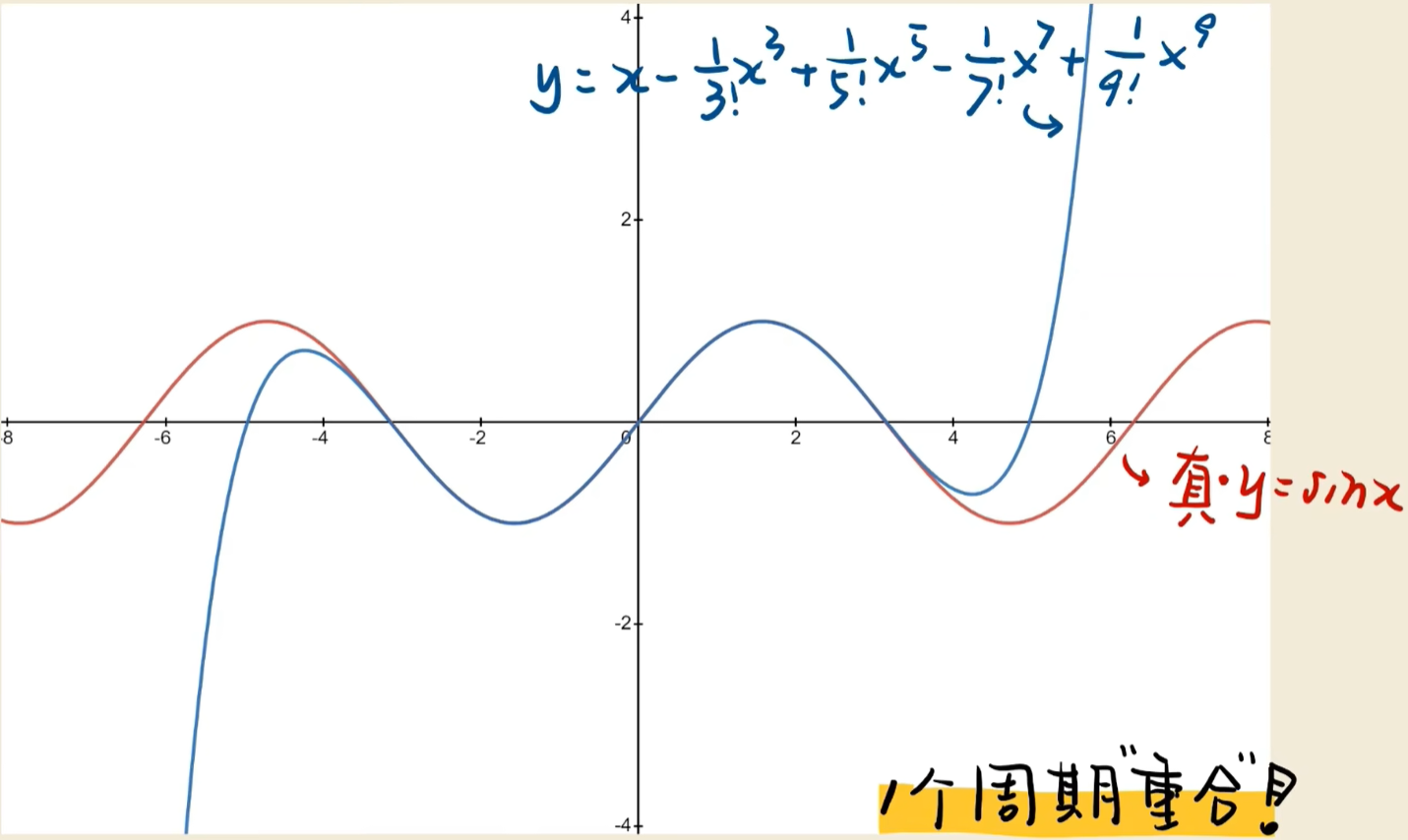
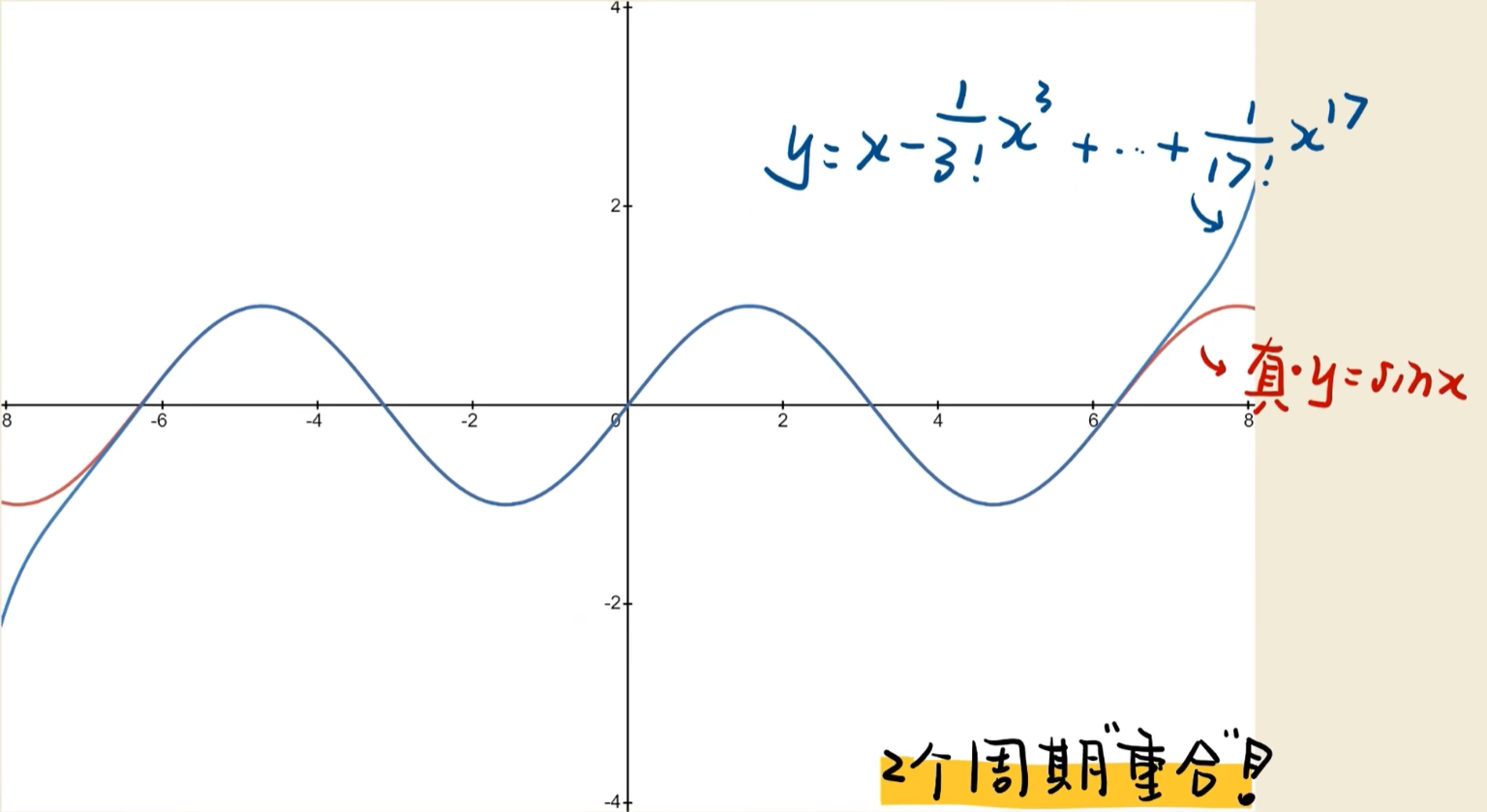
1:展开三角函数

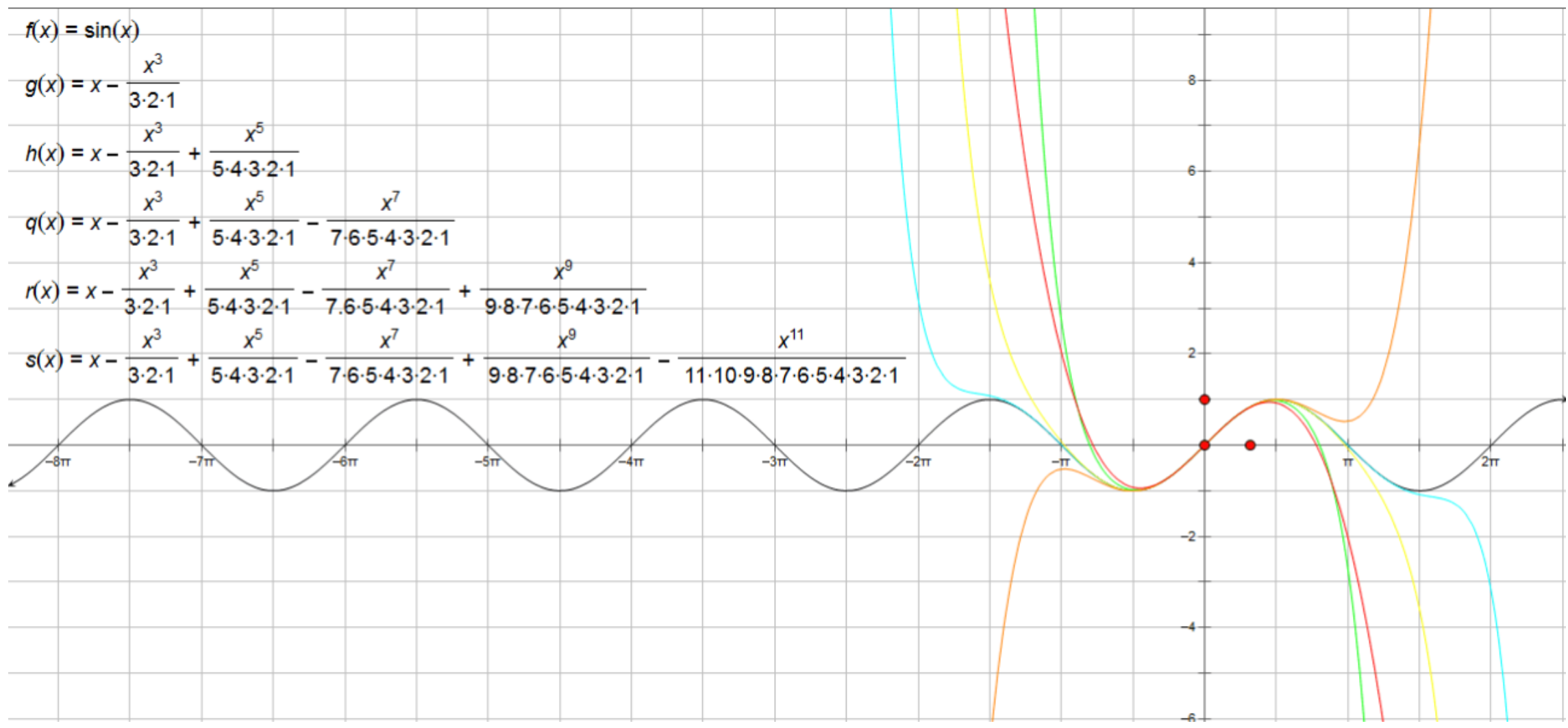
2.计算近似值
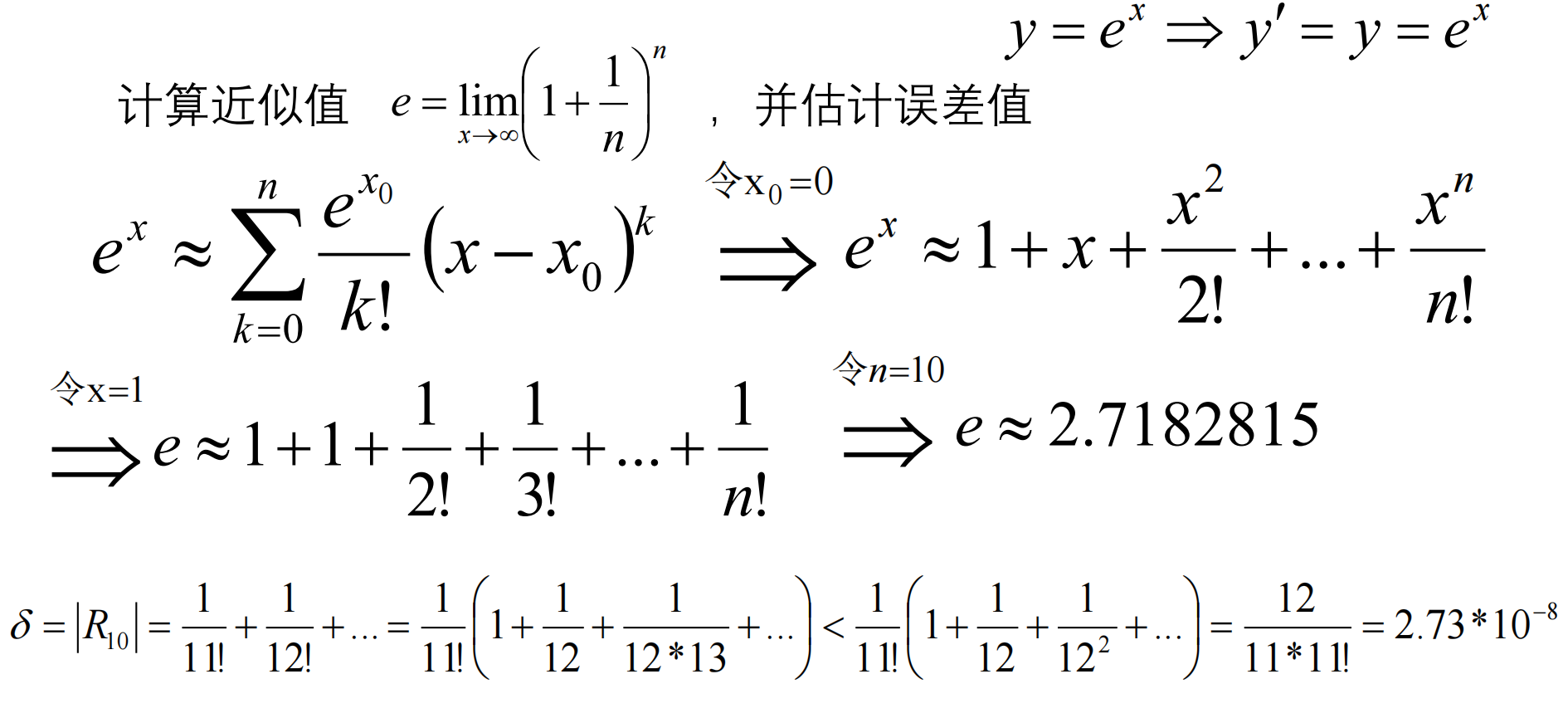
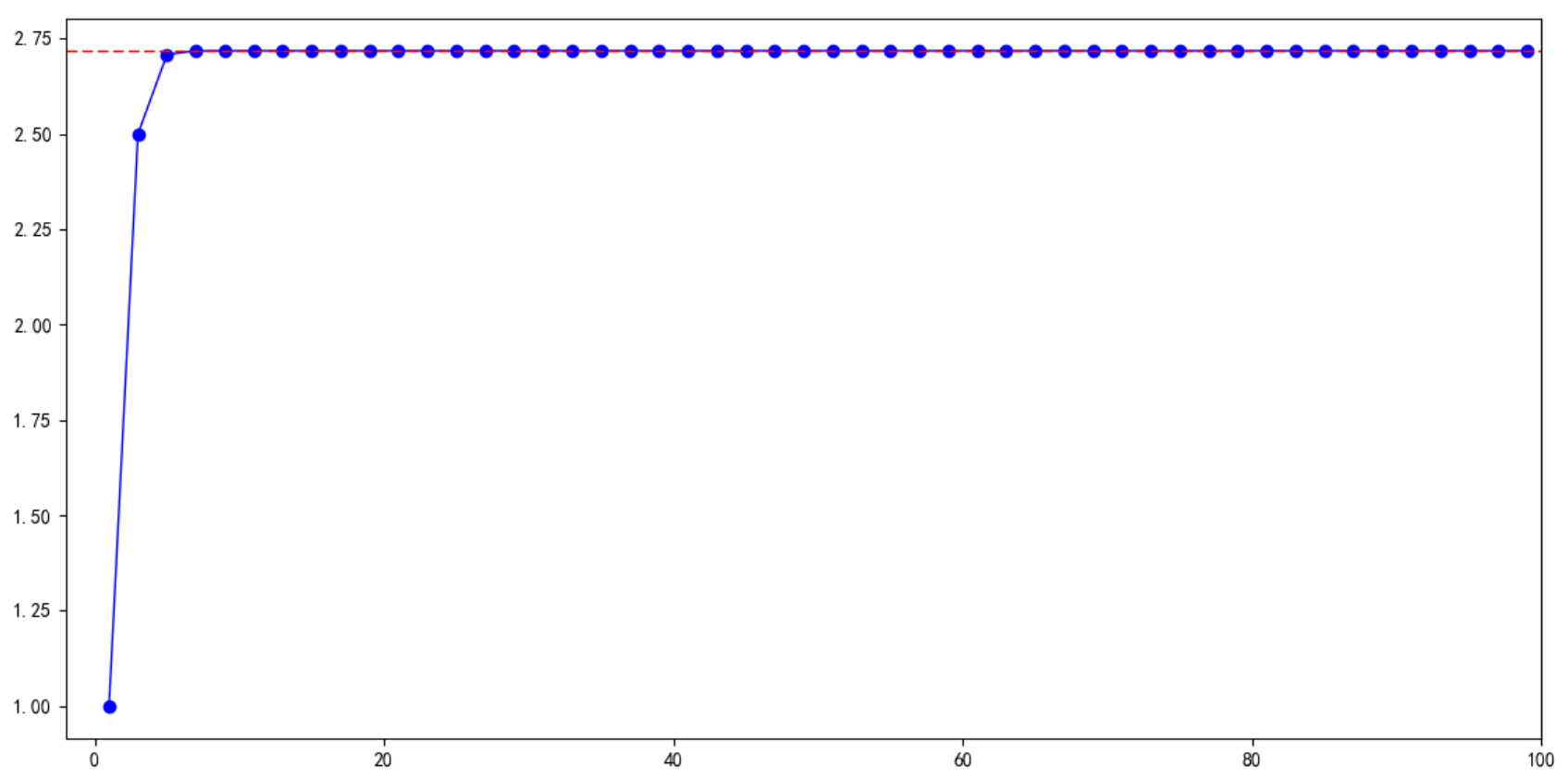
泰勒公式加深理解
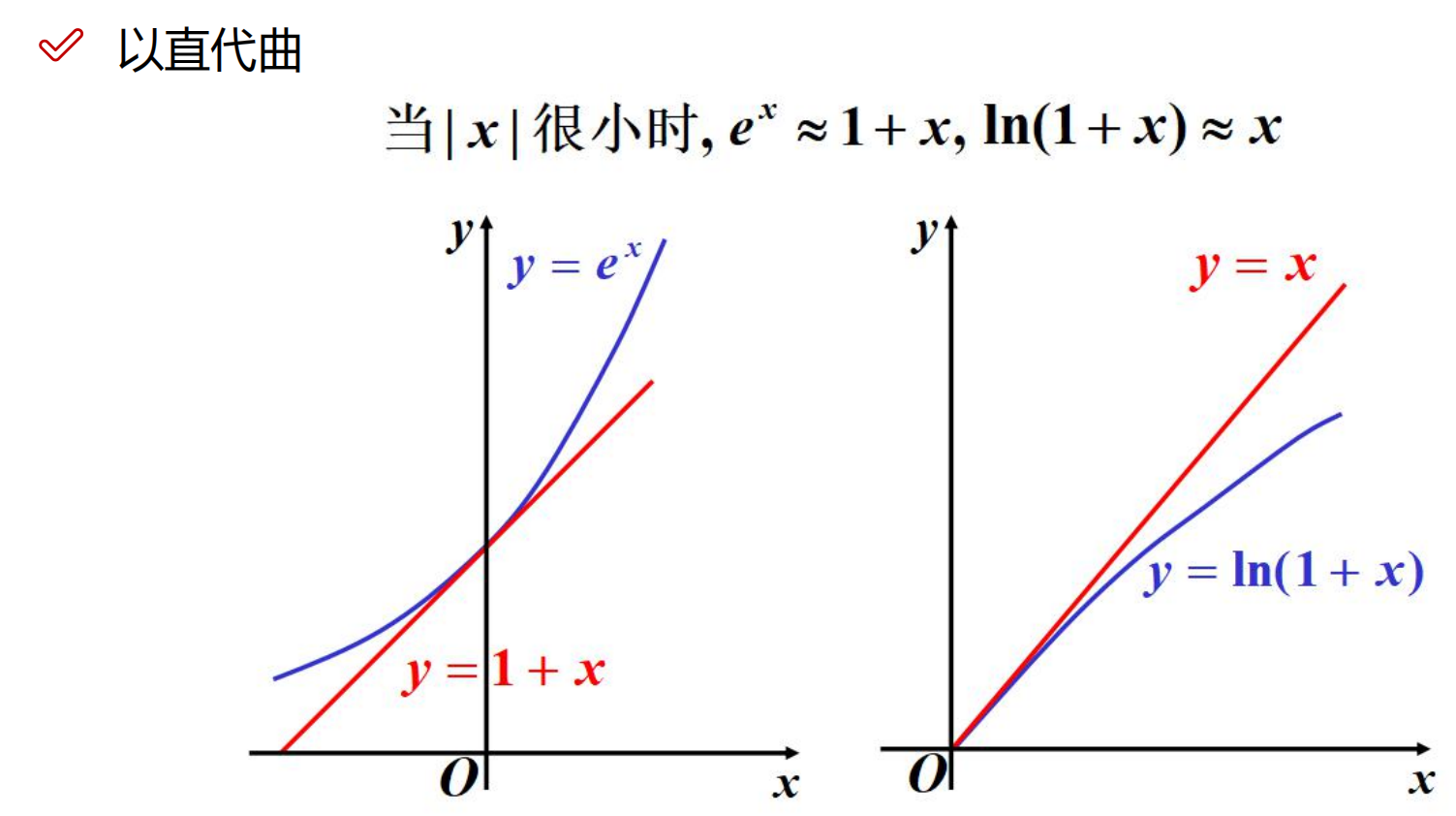
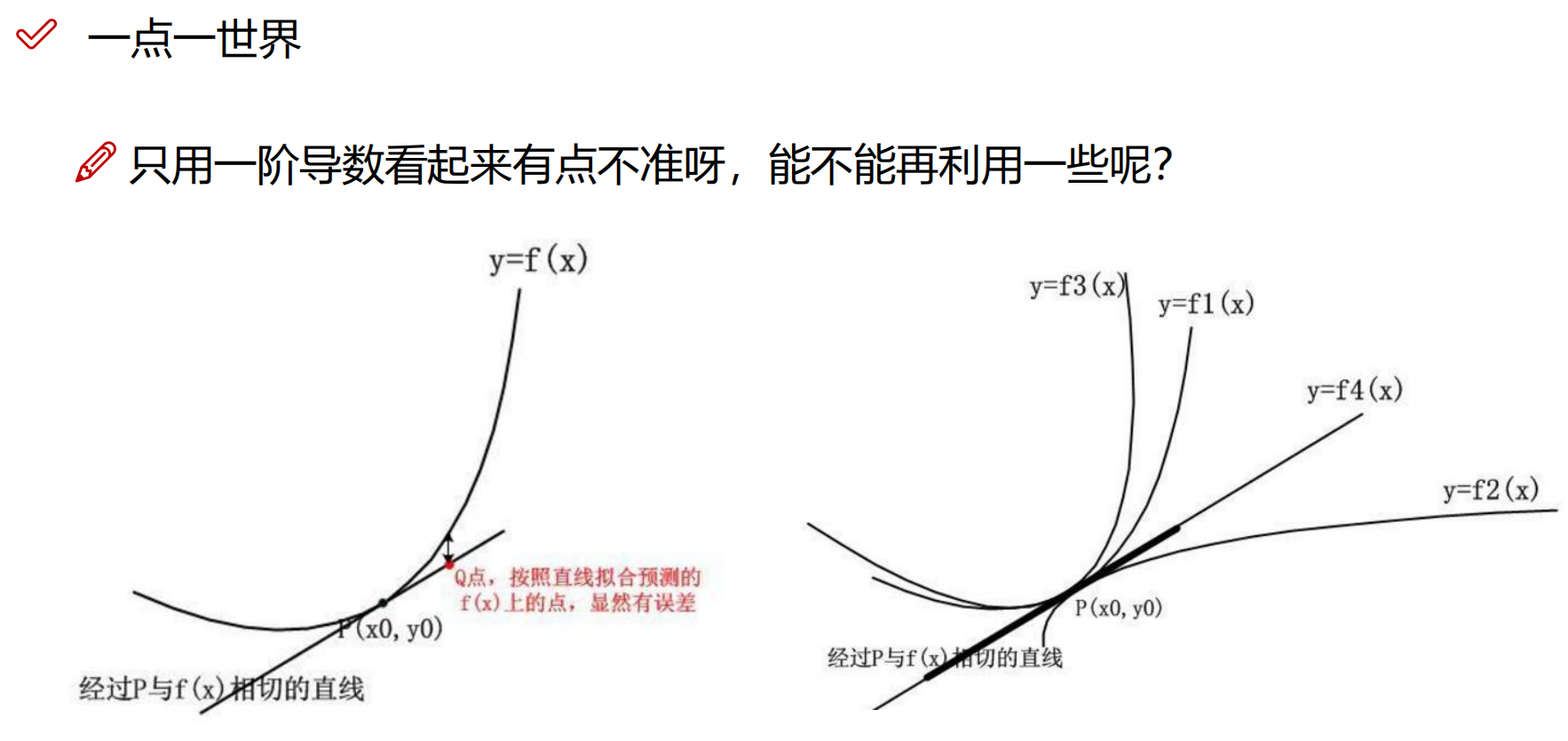
一阶导数只帮我们定位了下一个点是上升还是下降对之后的趋势就很难把控了
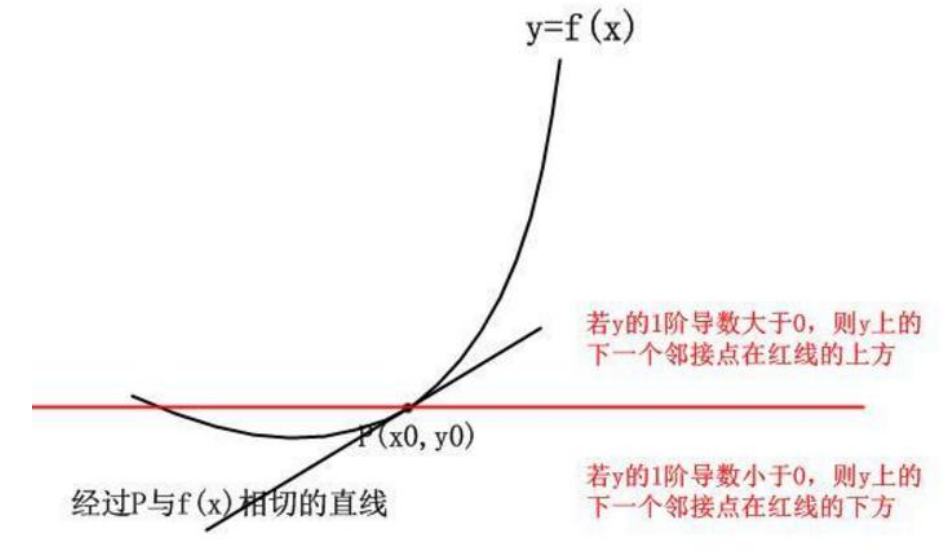
如何做的更准确一些呢?如果把二阶导利用上呢。
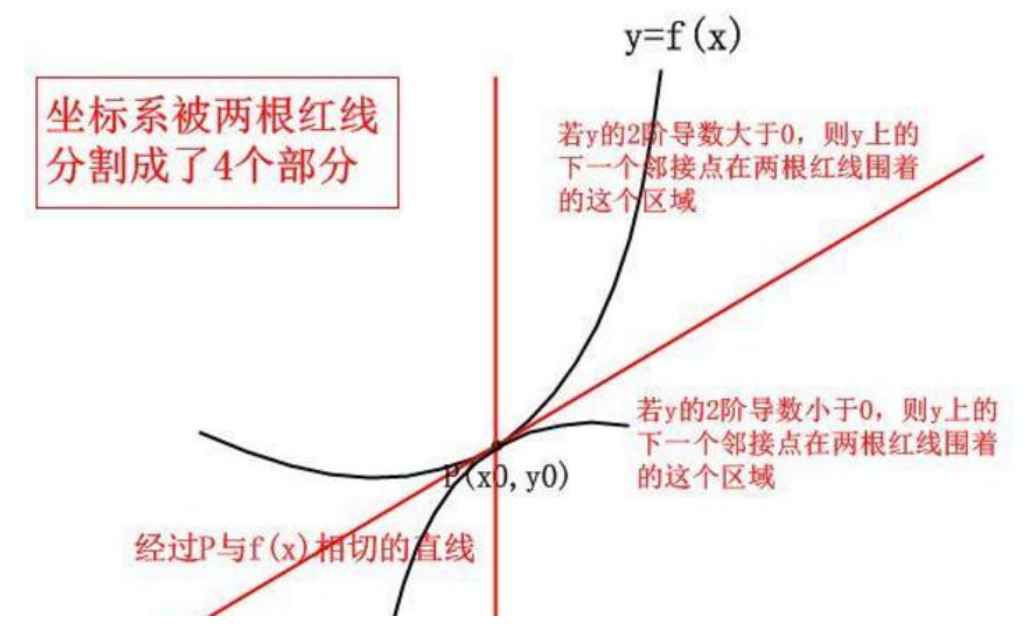

多项式逼近演示
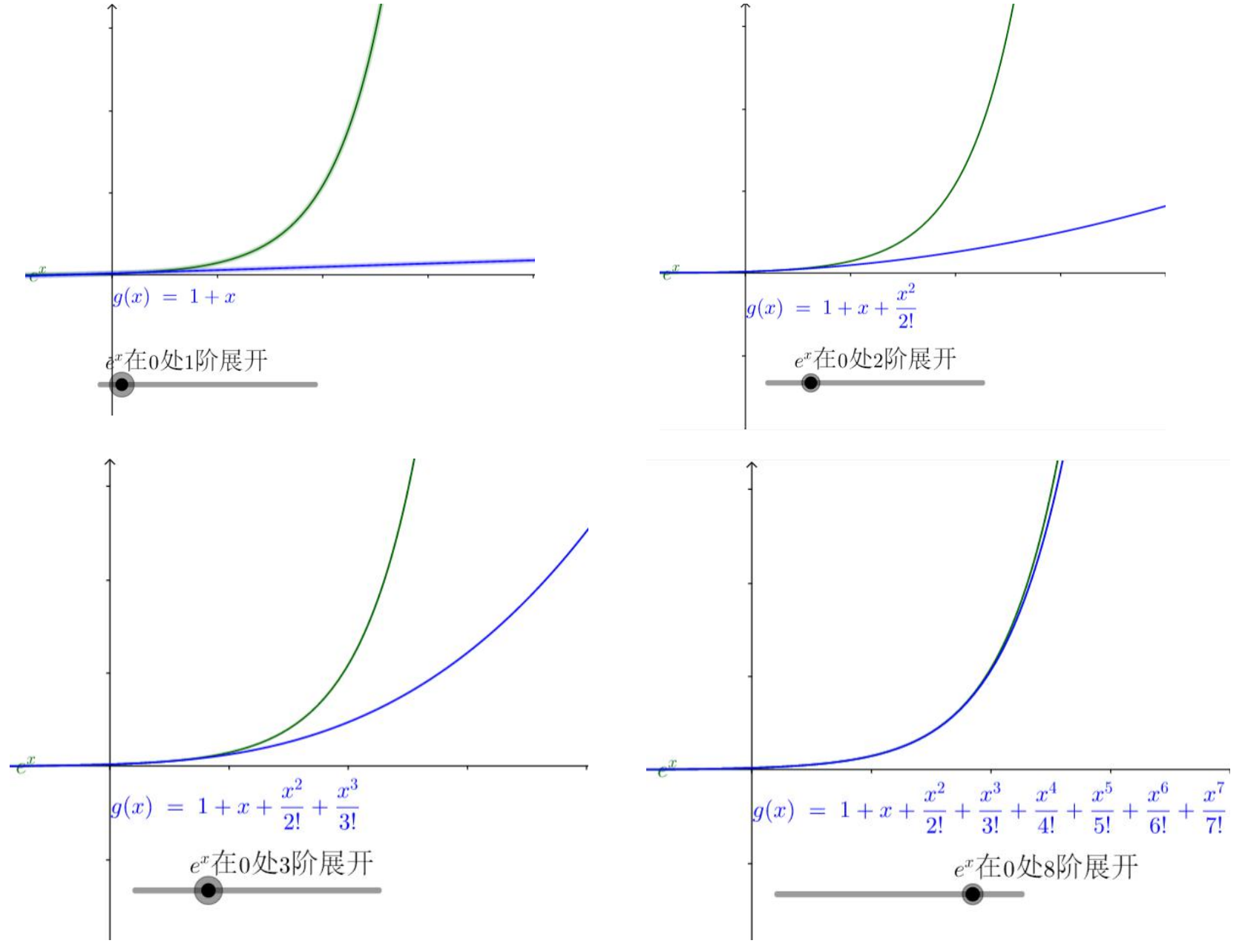
阶数
阶数越高增长速度越快。
观察可发现,越高次项在越偏右侧影响越大。
对于一个复杂函数,给我们的感觉是在当前点,低阶项能更好的描述当前点附近,对于之后的走势就越来越依靠高阶的了。
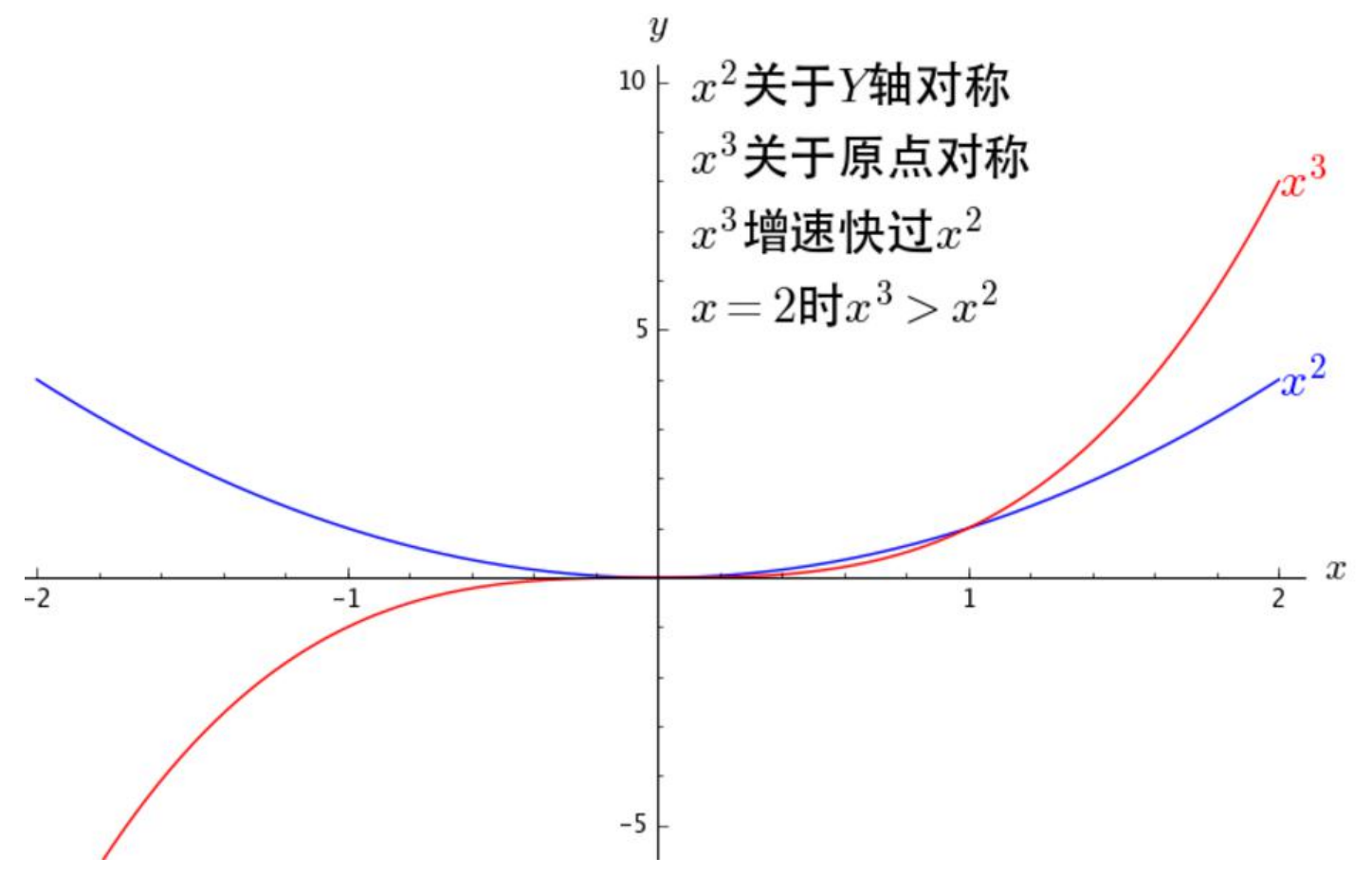
阶乘是什么意思呢?
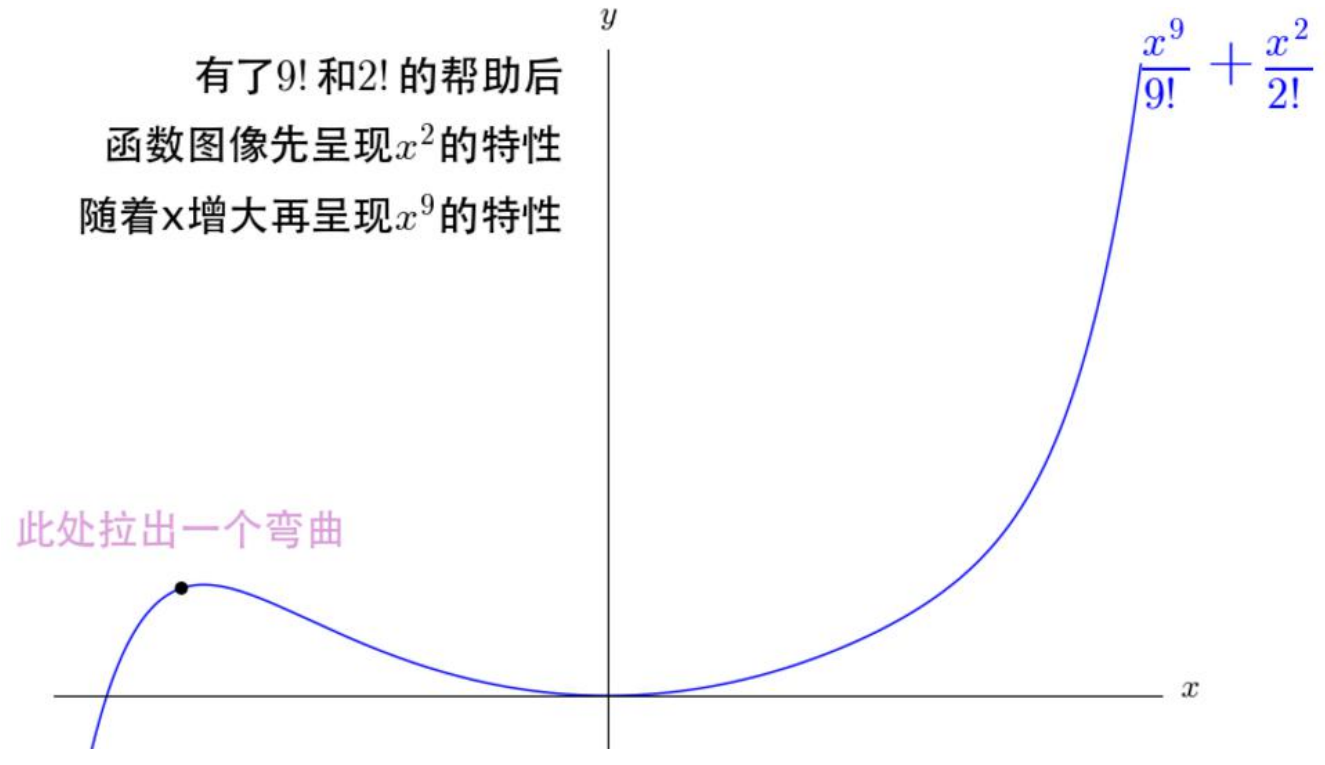
如果把9次的和2次的直接放在一起,那2次的就不用玩了。
但是在开始的时候应该是2次的效果更好,之后才是慢慢轮到9次的呀!
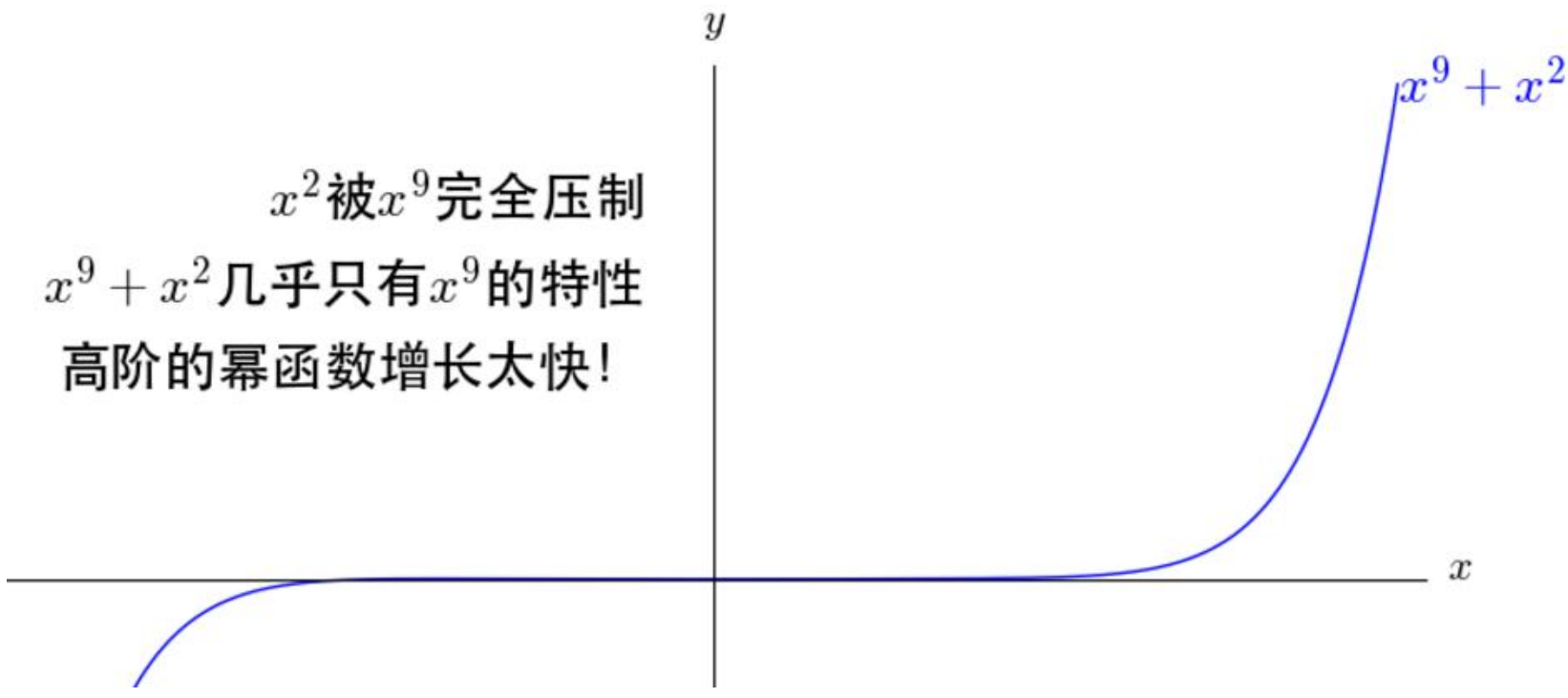
有了阶乘之后,就帮助我们解决了这样的问题。
练习





 浙公网安备 33010602011771号
浙公网安备 33010602011771号