K近邻算法(KNN)：机器学习入门必学算法

1 什么是K-近邻算法

根据你的“邻居”来推断出你的类别。

那么如何查找和你距离最近的邻居是哪个呢？这就要使用到最近邻与搜索。

最近邻域搜索（Nearest-Neighbor Lookup）

最近邻域搜索（Nearest-Neighbor Lookup，NNL）是一种在数据集中查找与给定查询点最相似（距离最近）的数据点的技术。

核心概念

目标：给定一个查询点（query point），在数据集中快速找到与之距离最近的一个或多个点。
距离度量：常用欧氏距离、曼哈顿距离、余弦相似度等。
变种：
- k-最近邻（k-NN）：返回前k个最近的点。
- 近似最近邻（Approximate Nearest Neighbor, ANN）：牺牲一定精度以提高搜索速度。

常用方法

线性扫描（Brute-Force）
- 原理：遍历所有数据点，计算距离并排序。
- 优点：实现简单，结果精确。
- 缺点：时间复杂度高（O(n)），不适合大规模数据。
空间划分数据结构
- KD树（K-Dimensional Tree）：
  - 递归地将数据空间划分为超矩形区域。
  - 适合低维数据（维度 < 20），搜索复杂度接近O(log n)。
- 球树（Ball Tree）：
  - 将数据划分为嵌套的超球体，适用于高维数据。
- 四叉树/八叉树：用于2D/3D空间数据。
哈希方法（Locality-Sensitive Hashing, LSH）
- 通过哈希函数将相似数据映射到同一哈希桶中。
- 适用于高维数据和大规模数据集，支持近似搜索。
图索引（如HNSW）
- 基于图结构的索引方法（Hierarchical Navigable Small World）。
- 在精度和速度之间平衡，被广泛应用于ANN任务。
量化方法（如PQ：Product Quantization）
- 将高维向量压缩为低维码本，减少存储和计算开销。

应用场景

分类与回归：k-NN算法直接基于最近邻结果进行预测。
图像/视频检索：根据特征向量查找相似内容。
推荐系统：基于用户或物品的相似性进行推荐。
异常检测：通过距离判断数据点是否异常。
地理信息系统（GIS）：查找最近的地标或路径。

挑战与优化

维度灾难（Curse of Dimensionality）：
- 高维数据中，距离计算效率下降，需使用降维技术（如PCA）或专用算法（如LSH）。
大规模数据：
- 采用分布式计算（如Spark、Faiss库）或近似算法。
动态数据更新：
- 某些数据结构（如KD树）对动态数据支持较差，需选择增量式方法。

常用工具库

Scikit-learn：提供k-NN、KD树、Ball Tree实现。
Faiss（Facebook AI Similarity Search）：高效的ANN库，支持GPU加速。
Annoy（Approximate Nearest Neighbors Oh Yeah）：轻量级ANN库。
HNSW：基于图的快速ANN算法实现。

K-近邻算法(KNN)概念

K Nearest Neighbor算法⼜叫KNN算法，这个算法是机器学习⾥⾯⼀个⽐较经典的算法，总体来说KNN算法是相对⽐较容易理解的算法

定义

如果⼀个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的⼤多数属于某⼀个类别，则该样本也属于这个类别。

来源：KNN算法最早是由Cover和Hart提出的⼀种分类算法

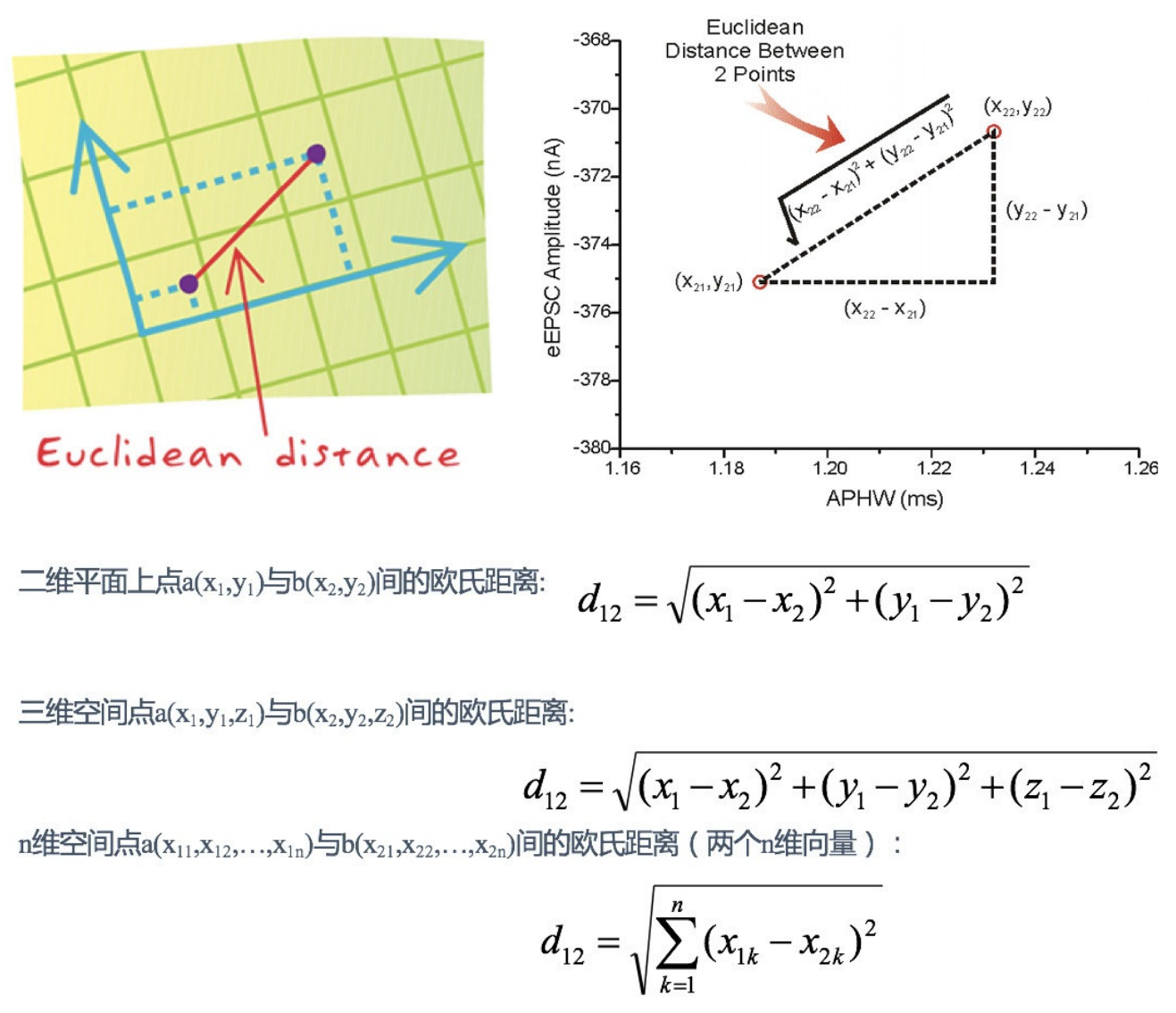
距离公式

两个样本的距离可以通过如下公式计算，⼜叫欧式距离，关于距离公式会在后⾯进⾏讨论

电影类型分析

假设我们现在有⼏部电影

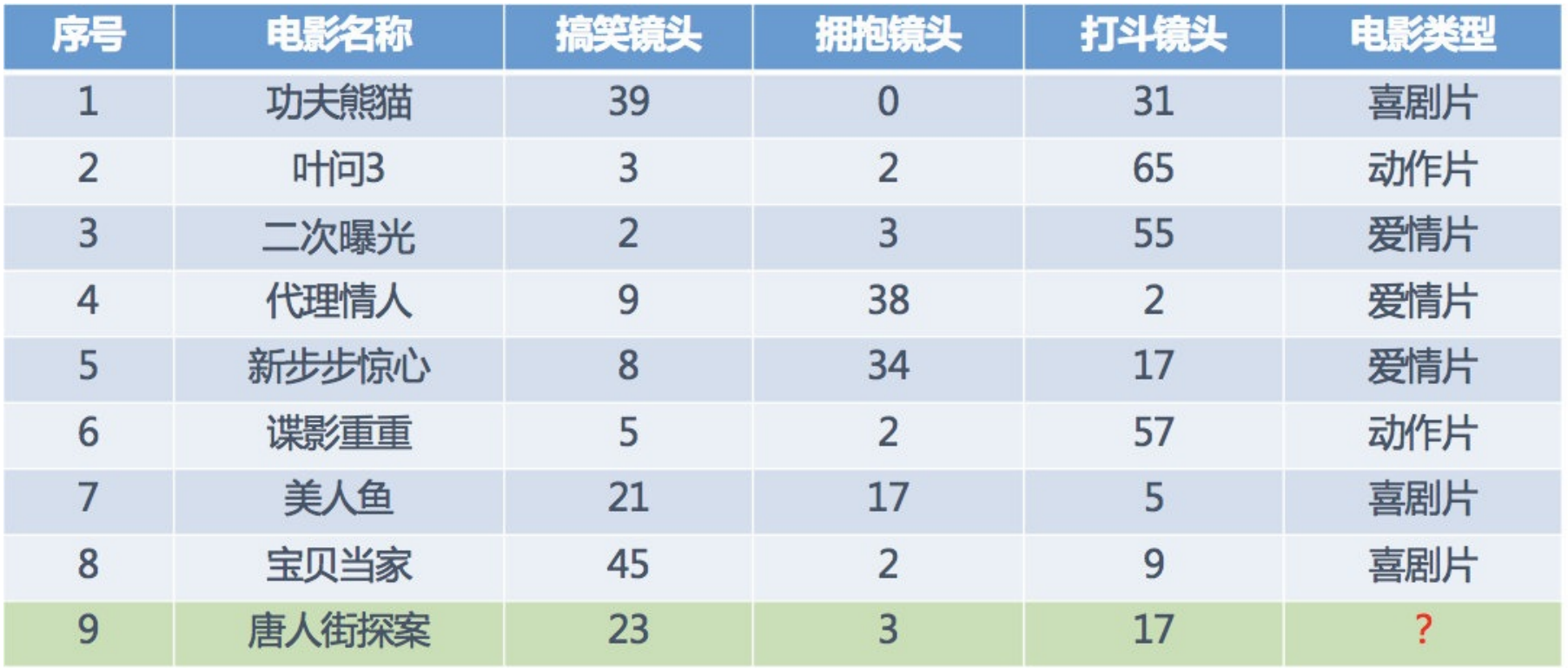
其中？ 9号电影不知道类别，如何去预测？我们可以利⽤K近邻算法的思想

分别计算每个电影和被预测电影的距离，然后求解

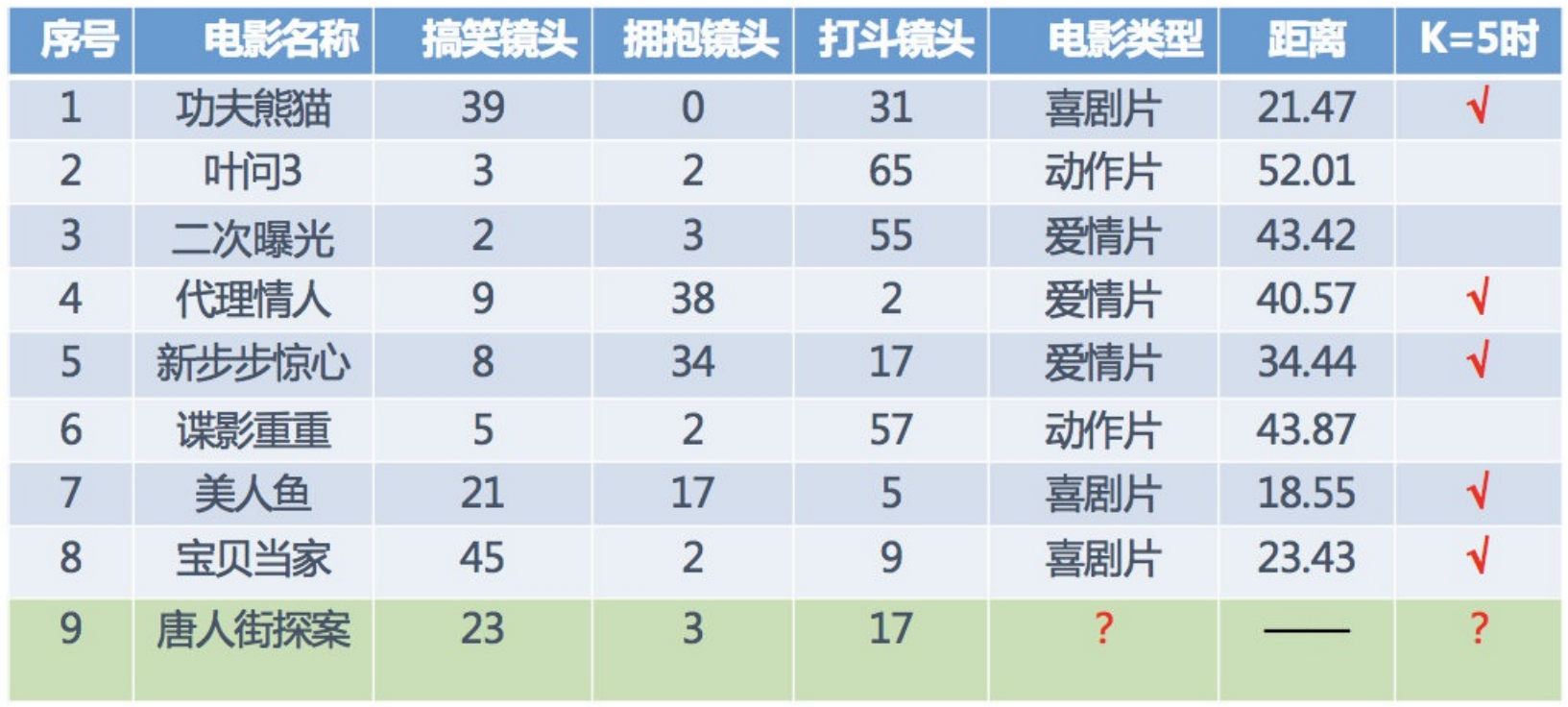
KNN算法流程总结

1）计算已知类别数据集中的点与当前点之间的距离

2）按距离递增次序排序

3）选取与当前点距离最⼩的k个点

4）统计前k个点所在的类别出现的频率

5）返回前k个点出现频率最⾼的类别作为当前点的预测分类

近邻算法的原理及scikit-learn-API介绍

最近邻（nearest neighbor）方法的原理是找到预定数量的距离新点最近的训练样本，并据此预测新点的标签。

样本数量可以是用户定义的常数（k-nearest neighbor learning：KNN既K近邻算法），也可以基于点的局部密度变化（radius-based neighbor learning：基于半径的邻域学习）。

距离通常可以是任何度量标准：标准欧氏距离是最常见的选择（详情参见距离度量）。

基于邻域的方法被称为非泛化的机器学习方法，因为它们只是“记住”所有训练数据（可能将其转换为快速索引结构，例如 Ball Tree或KD Tree）。

尽管最近邻方法简单，但它已在大量分类和回归问题中取得了成功，包括手写数字和卫星图像场景。作为一种非参数方法，它通常在决策边界非常不规则的分类情况下取得成功。

核心概念

基于实例的学习 (Instance-based Learning)
不构建通用内部模型，而是直接存储训练数据实例。分类结果通过查询点的最近邻投票决定。
- 分类规则：多数投票法，即查询点的类别由其最近邻中占比最高的类别决定。
非泛化学习 (Non-generalizing Learning)
依赖训练数据的局部结构，而非全局模型，适用于动态或小规模数据集。

scikit-learn-API(分类器)

分类器类型	原理	适用场景
`KNeighborsClassifier`	基于每个查询点的 `k` 个最近邻（`k` 为用户指定的整数）。	数据均匀分布、维度适中时效果最佳。需平衡 `k` 值： - 较大的 `k` 抑制噪声，但分类边界模糊。 - 较小的 `k` 对噪声敏感，边界更清晰。
`RadiusNeighborsClassifier`	基于每个查询点固定半径 `r` 内的所有邻居（`r` 为用户指定的浮点数）。	数据非均匀采样（如稀疏和密集区域并存）。高维数据不适用（维度灾难导致半径内邻居过少）。

参数选择与影响

k 值的选择

数据依赖性高：需通过交叉验证调优。
权衡点：噪声抑制 vs. 边界清晰度。
K值过⼩：
- 容易受到异常点的影响（假设k=1，而目标数据正好离一个异常值比较近，那就会得出错误的结论）
- 容易过拟合
k值过⼤：
- 受到样本均衡影响的问题（假设k=n，即所有数据总条数，那么，如果数据不均衡，例如一个班级男生很多，女生很少，那么大概率会把目标学生判定为男生）
- 容易⽋拟合
在实际应⽤中，K值⼀般取⼀个⽐较⼩的数值，例如采⽤交叉验证法（简单来说，就是把训练数据再分成两组:训练集和验证集）来选择最优的K值。
近似误差：
- 对现有训练集的训练误差，关注训练集，
- 如果近似误差过⼩可能会出现过拟合的现象，对现有的训练集能有很好的预测，但是对未知的测试样本将会出现较⼤偏差的预测。
- 模型本身不是最接近最佳模型。
估计误差：
- 可以理解为对测试集的测试误差，关注测试集，
- 估计误差⼩说明对未知数据的预测能⼒好，
- 模型本身最接近最佳模型。

半径 r 的局限性

维度灾难：高维空间中，所有点距离趋同，半径内可能无有效邻居。
稀疏数据优势：在密度差异大的数据中，自动调整局部邻居数量。

权重机制

通过 weights 参数控制邻居对分类的贡献权重：

weights='uniform'（默认）：所有邻居权重相等（简单多数投票）。
weights='distance'：权重与距离成反比（近邻影响更大）。
自定义函数：用户可定义距离函数，灵活调整权重计算逻辑。

优缺点对比

优点	缺点
简单易实现，无需训练过程。	计算成本高（需存储全部数据并实时计算距离）。
适应复杂决策边界和非线性数据。	高维数据效果差（维度灾难）。
支持动态更新（新增数据无需重新训练）。	参数选择敏感（`k` 或 `r` 需精细调优）。

应用场景

小规模数据分类：如垃圾邮件检测、图像分类（MNIST 手写数字）。
动态数据环境：数据频繁更新时，避免重复训练模型。
非均匀数据：如地理空间数据、客户分群中的稀疏密集混合分布。

关键总结

适用性优先：均匀数据选 KNN，非均匀数据选 Radius，高维数据慎用。
调参核心：平衡噪声抑制与边界清晰度，交叉验证优化 k 或 r。
计算优化：使用树结构（kd_tree/ball_tree）加速近邻搜索。

注：实际应用中需结合数据预处理（如标准化）和降维技术（PCA）提升效果。

距离度量

参照《常见距离度量方式》

kd树

问题导⼊：

根据KNN每次需要预测⼀个点时，我们都需要计算训练数据集⾥每个点到这个点的距离，然后选出距离最近的k个点进⾏投票。

当数据集很⼤时，这个计算成本⾮常⾼，针对N个样本，D个特征的数据集，当需要预测所有 $N$ 个样本点的类别时，其算法复杂度为O（DN²）。【单次预测的总复杂度： $O (D N)$ 。】

实现k近邻算法时，主要考虑的问题是如何对训练数据进⾏快速k近邻搜索。这在特征空间的维数⼤及训练数据容量⼤时尤其必要。

k近邻法最简单的实现是线性扫描（穷举搜索），即要计算输⼊实例与每⼀个训练实例的距离。计算并存储好以后，再查找K近邻。当训练集很⼤时，计算⾮常耗时。

为了提⾼KNN搜索的效率，可以考虑使⽤特殊的结构存储训练数据，以减⼩计算距离的次数,KD树就是其中一直存储结构。

简介

kd树(K-dimension tree)是⼀种对k维空间中的实例点进⾏存储以便对其进⾏快速检索的树形数据结构。kd树是⼀种⼆叉树，表示对k维空间的⼀个划分，构造kd树相当于不断地⽤垂直于坐标轴的超平⾯将K维空间切分，构成⼀系列的K维超矩形区域。kd树的每个结点对应于⼀个k维超矩形区域。利⽤kd树可以省去对⼤部分数据点的搜索，从⽽减少搜索的计算量。

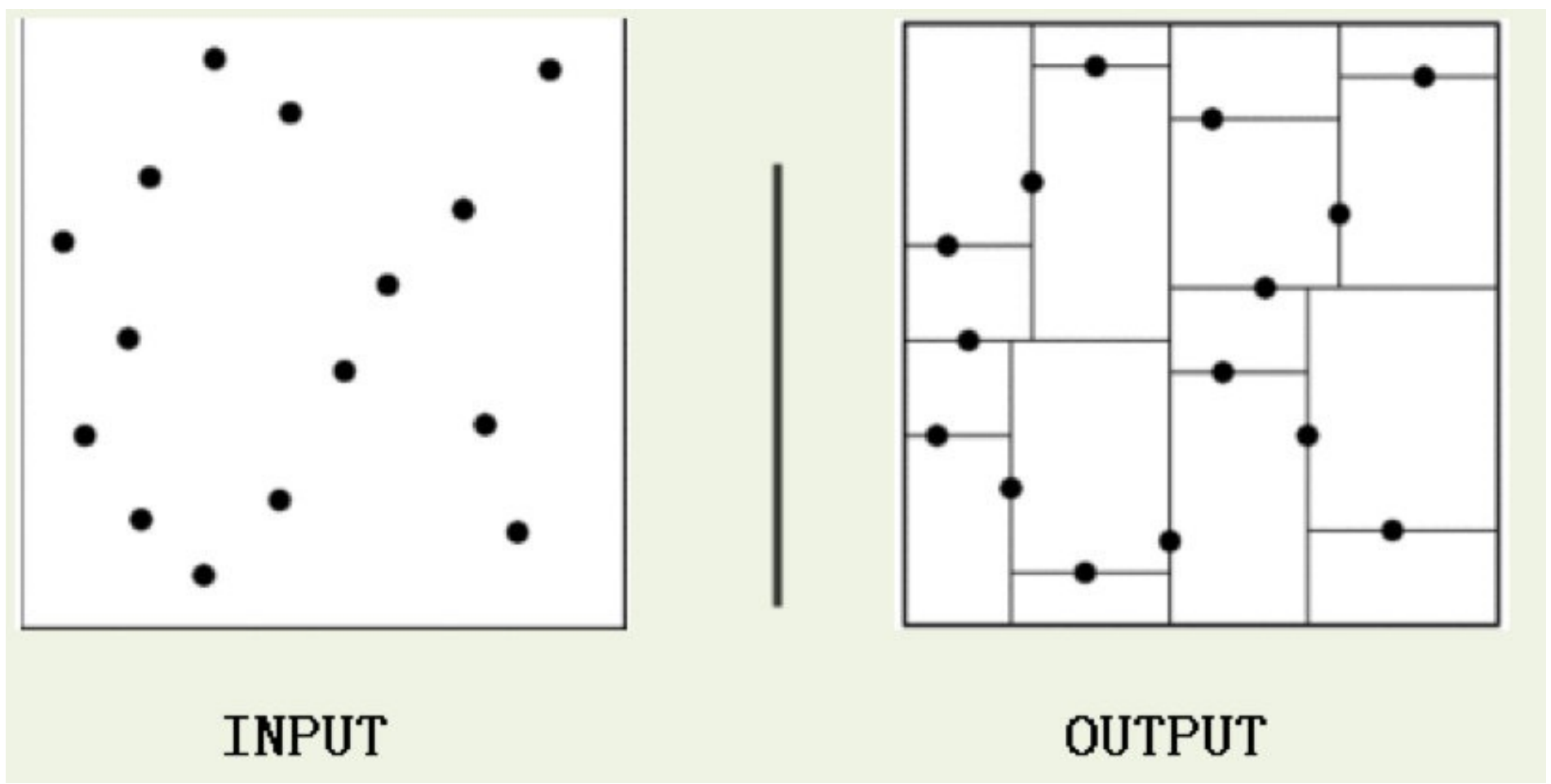
类⽐“⼆分查找”：给出⼀组数据：[9 1 4 7 2 5 0 3 8]，要查找8。如果挨个查找（线性扫描），那么将会把数据集都遍历⼀遍。⽽如果排⼀下序那数据集就变成了：[0 1 2 3 4 5 6 7 8 9]，按前⼀种⽅式我们进⾏了很多没有必要的查找，现在如果我们以5为分界点，那么数据集就被划分为了左右两个“簇” [0 1 2 3 4]和[6 7 8 9]。

因此，根本就没有必要进⼊第⼀个簇，可以直接进⼊第⼆个簇进⾏查找。把⼆分查找中的数据点换成k维数据点，这样的划分就变成了⽤超平⾯对k维空间的划分。空间划分就是对数据点进⾏分类，“挨得近”的数据点就在⼀个空间⾥⾯。

这样优化后的算法复杂度可降低到O（DNlog（N））（注： log_b(N) = k，则等价于 N = b^k。 $N = 8$ ， $b = 2$ ，则： $k = log 2 (8) = 3$ ）。感兴趣的读者可参阅论⽂：Bentley，J.L.，Communications ofthe ACM（1975）。

1989年，另外⼀种称为Ball Tree的算法，在kd Tree的基础上对性能进⼀步进⾏了优化。感兴趣的读者可以搜索Five balltree construction algorithms来了解详细的算法信息。

原理

其基本原理是，如果A和B距离很远，B和C距离很近，那么A和C的距离也很远。有了这个信息，就可以在合适的时候跳过距离远的点。

构造步骤

选点与切分

在一堆数字中，选择一个中间的数字（一般是中位数），例如下面的‘2’作为分割点，将数字分成两部分，然后左右两部分再依次以中间数未分割点进行分割，直到最后只有一个数字无法再分为止。

好的划分⽅法可以使构建的树⽐较平衡，可以每次选择中位数来进⾏划分。

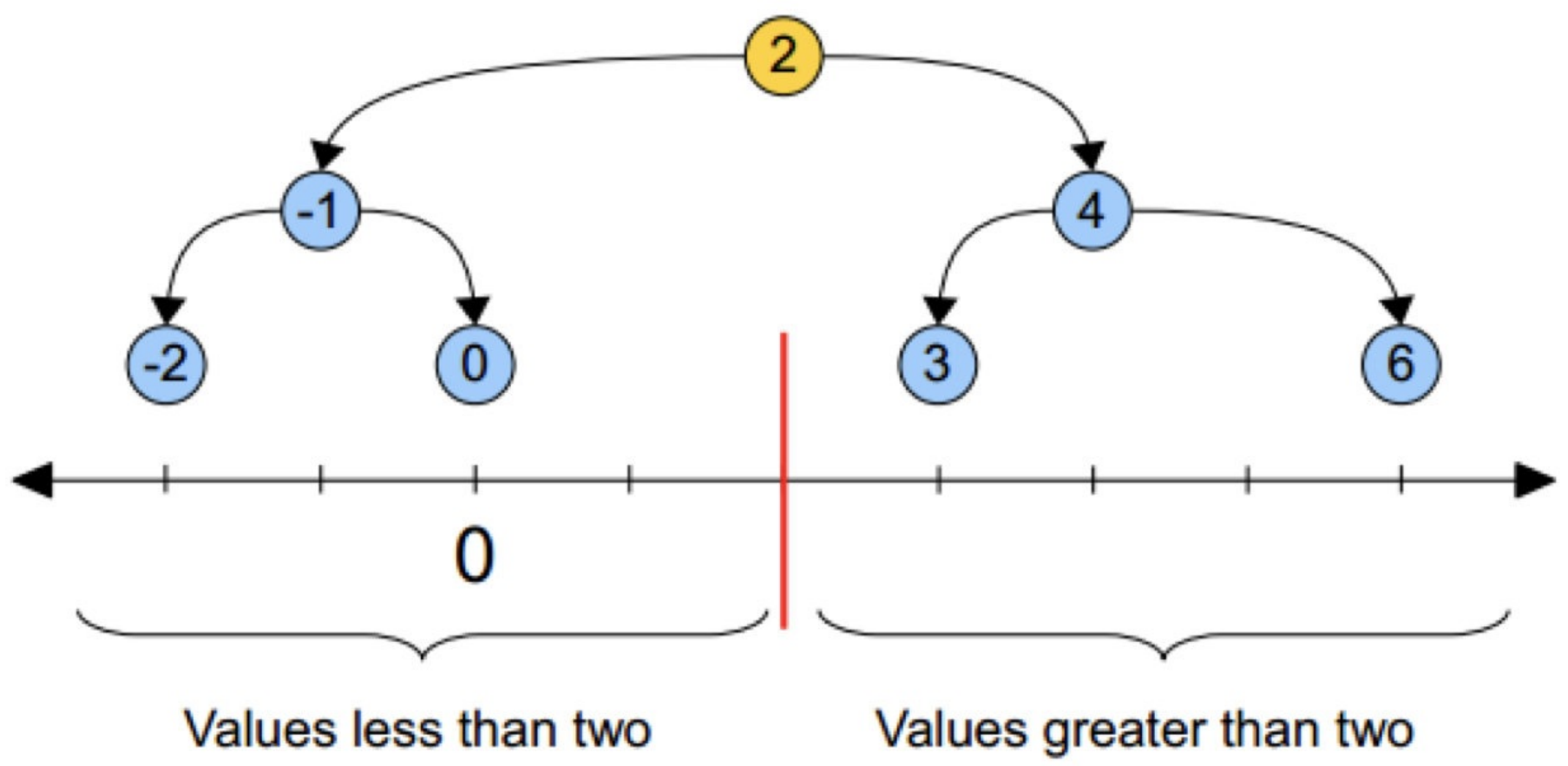
如下图：⻩⾊的点作为根节点，上⾯的点归左⼦树，下⾯的点归右⼦树，接下来再不断地划分，分割的那条线叫做分割超平⾯（splitting hyperplane），在⼀维中是⼀个点，⼆维中是线，三维的是⾯。

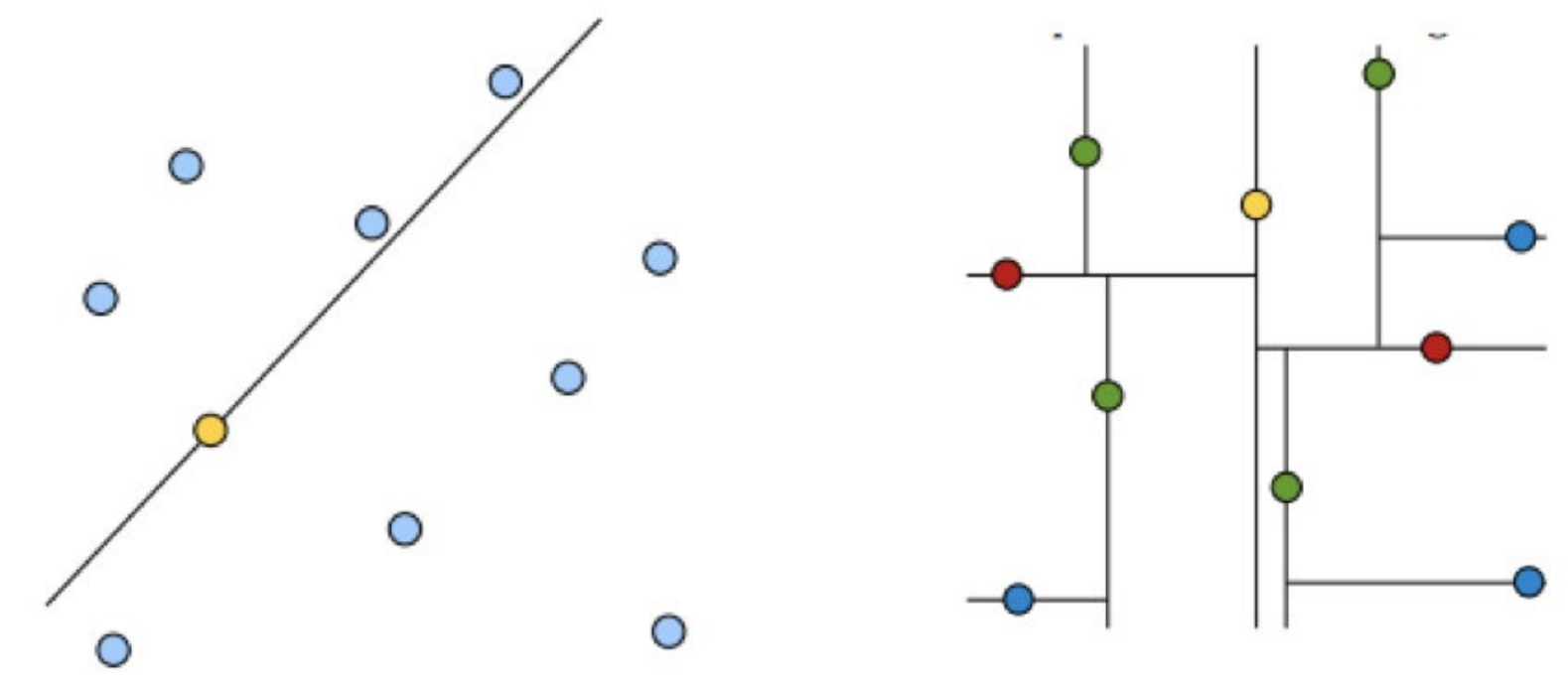
⻩⾊节点就是Root节点，下⼀层是红⾊，再下⼀层是绿⾊，再下⼀层是蓝⾊。

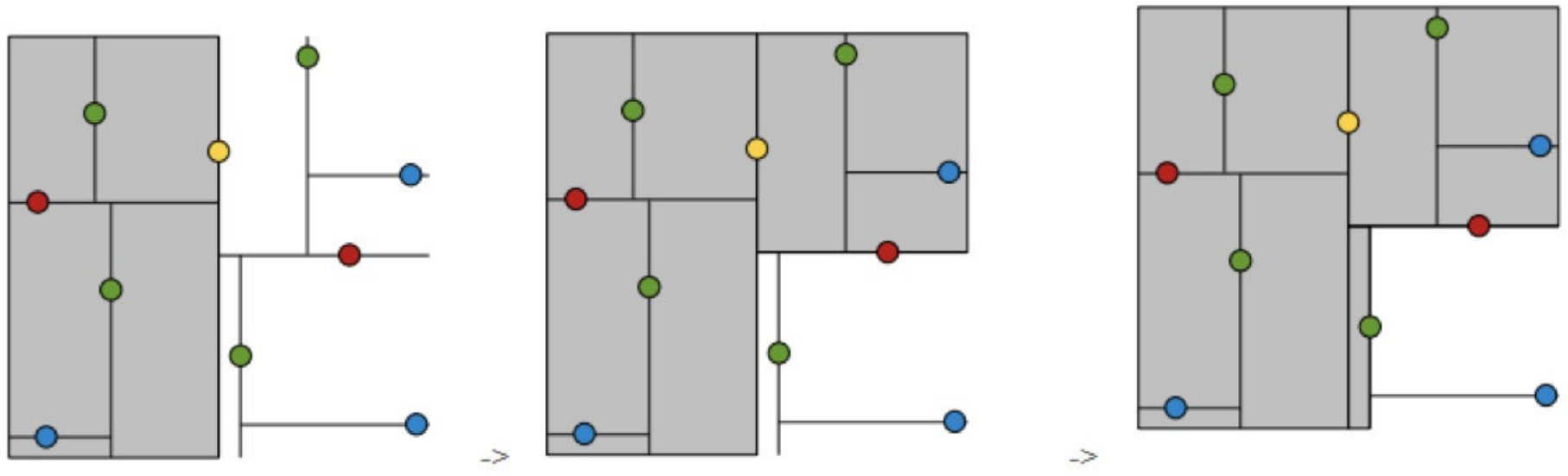
维度选择

KD树中每个节点是⼀个向量，和⼆叉树按照数的⼤⼩划分不同的是，KD树每层需要选定向量中的某⼀维，然后根据这⼀维按左⼩右⼤的⽅式划分数据。那么选择向量的哪⼀维进⾏划分嗯？

简单的解决⽅法可以是随机选择某⼀维或按顺序选择，但是更好的⽅法应该是在数据⽐较分散的那⼀维进⾏划分（分散的程度可以根据⽅差来衡量）。

总结

（1）构造根结点，使根结点对应于K维空间中包含所有实例点的超矩形区域；

（2）通过递归的⽅法，不断地对k维空间进⾏切分，⽣成⼦结点。在超矩形区域上选择⼀个坐标轴和在此坐标轴上的⼀个切分点，确定⼀个超平⾯，这个超平⾯通过选定的切分点并垂直于选定的坐标轴，将当前超矩形区域切分为左右两个⼦区域（⼦结点）；这时，实例被分到两个⼦区域。

（3）上述过程直到⼦区域内没有实例时终⽌（终⽌时的结点为叶结点）。在此过程中，将实例保存在相应的结点上。

（4）回溯

通常，循环的选择坐标轴对空间切分，选择训练实例点在坐标轴上的中位数为切分点，这样得到的kd树是平衡的（平衡⼆叉树：它是⼀棵空树，或其左⼦树和右⼦树的深度之差的绝对值不超过1，且它的左⼦树和右⼦树都是平衡⼆叉树）。

案例分析

注意，下图中的x（2）其实就是y，记住，方便理解

树的建⽴

给定⼀个⼆维空间数据集：T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}，构造⼀个平衡kd树。

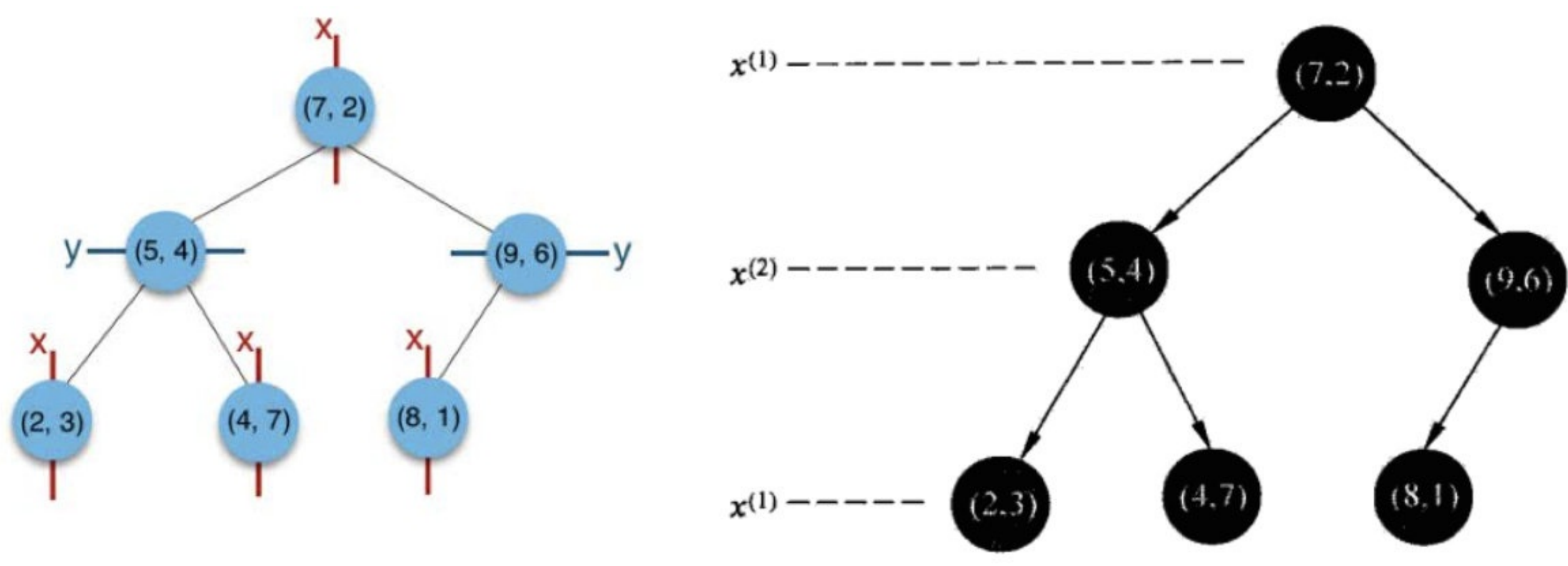
（1）思路引导：

X=[2,5,9,4,8,7]=[2,4,5,7,8,9]

Y=[3,4,6,7,1,2]=[1,2,3,4,6,7]

6个数据点的x(1)坐标中位数是6，这⾥选最接近的(7,2)或者（5,4）点，以平⾯x(1)=7将空间分为左、右两个⼦矩形（⼦结点）；

第一次按照x值划分，划分之后（以右侧为例）x=[2,4,5],y=[3,4,7],很显然，此时y轴维度的方差要大于x，所以接下来按照y维度进行划分，[3,4,7]的中位数是4，对应的x是5，所以以（5,4）划分。。。

如此递归，最后得到如下图所示的特征空间划分和kd树。

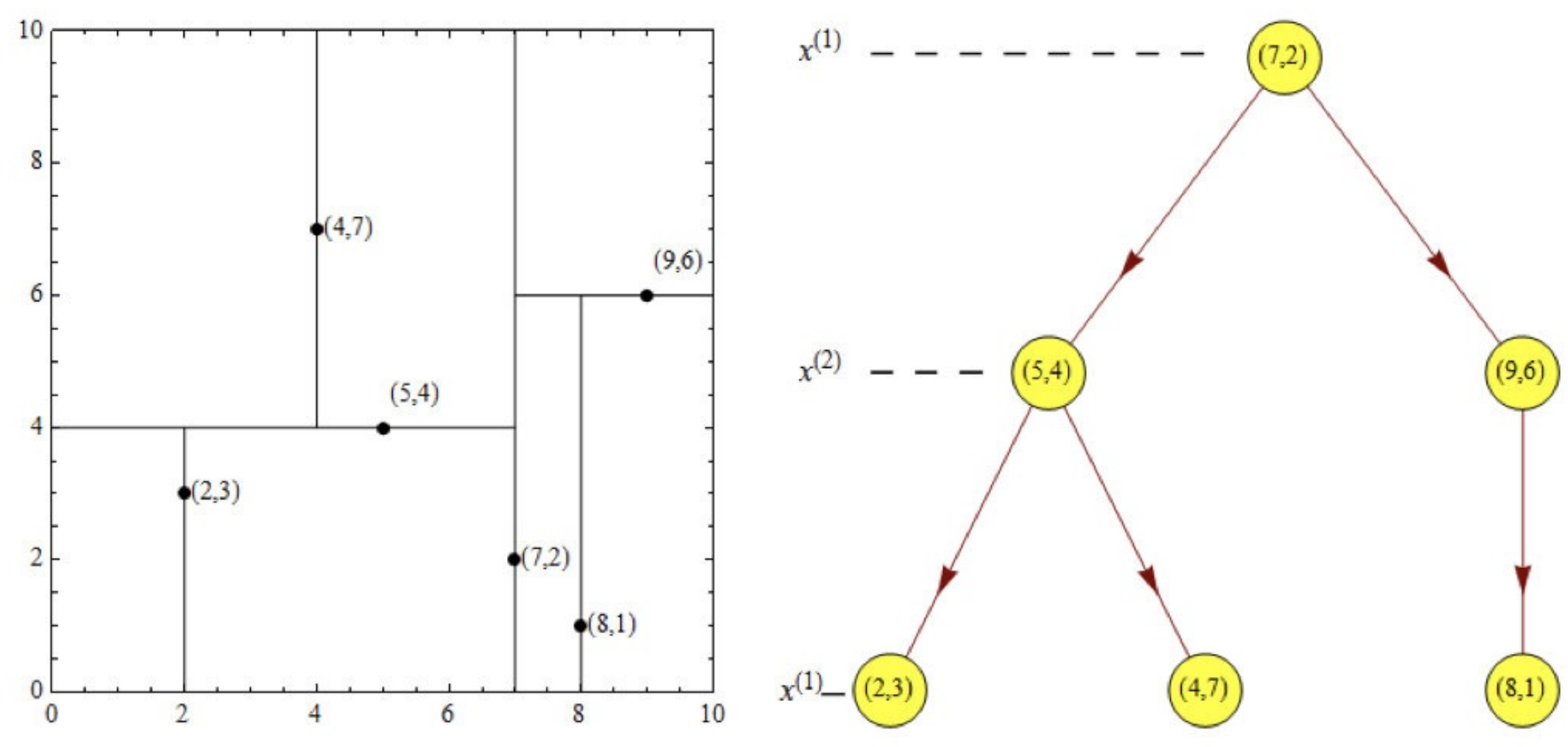
回溯

假设标记为星星的点是 test point，绿⾊的点是找到的近似点，在回溯过程中，需要⽤到⼀个队列，存储需要回溯的点，在判断其他⼦节点空间中是否有可能有距离查询点更近的数据点时，做法是以查询点为圆⼼，以当前的最近距离为半径画圆，这个圆称为候选超球（candidate hypersphere），如果圆与回溯点的轴相交，则需要将轴另⼀边的节点都放到回溯队列⾥⾯来。

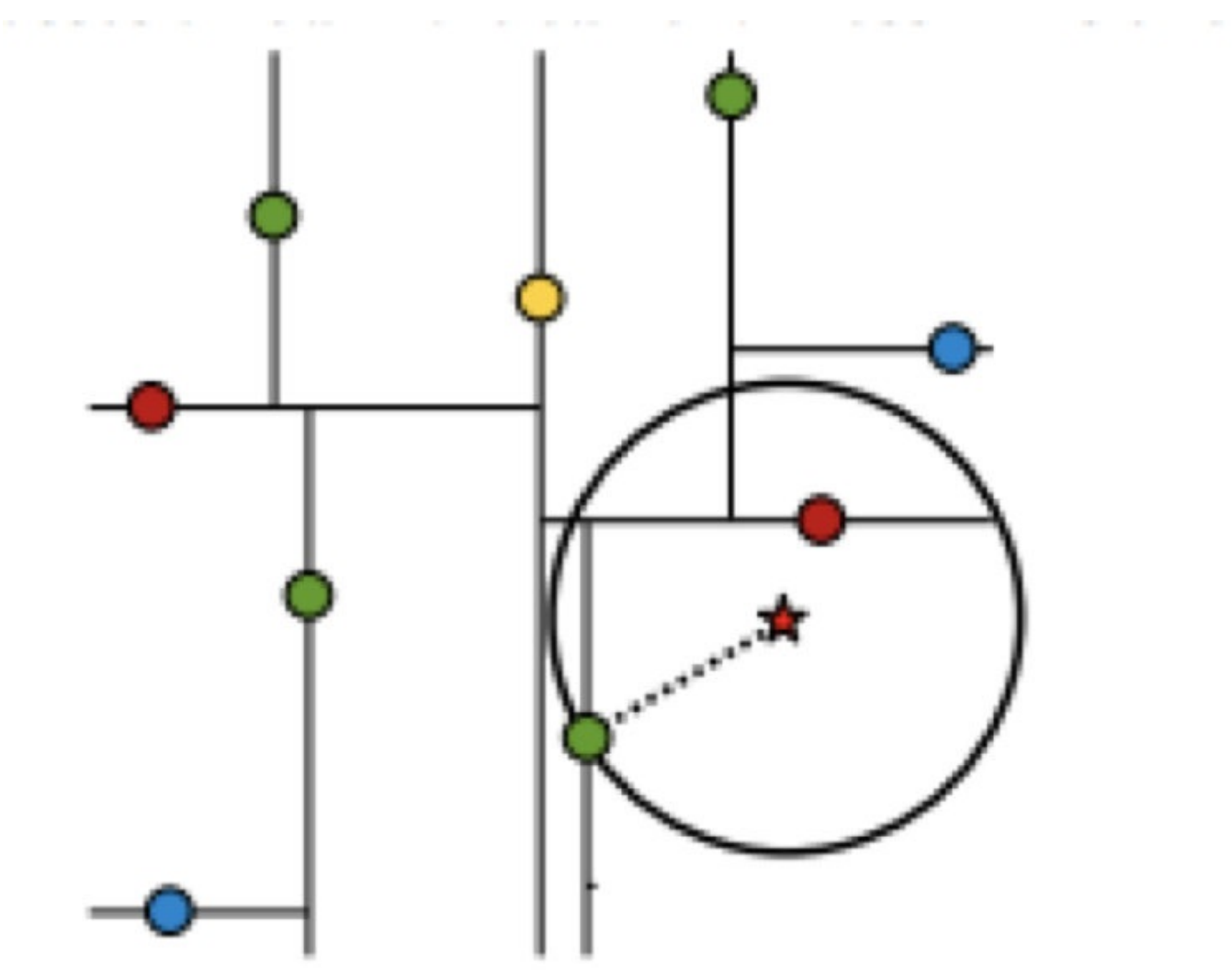
样本集{(2,3),(5,4), (9,6), (4,7), (8,1), (7,2)}

查找点(2.1,3.1)

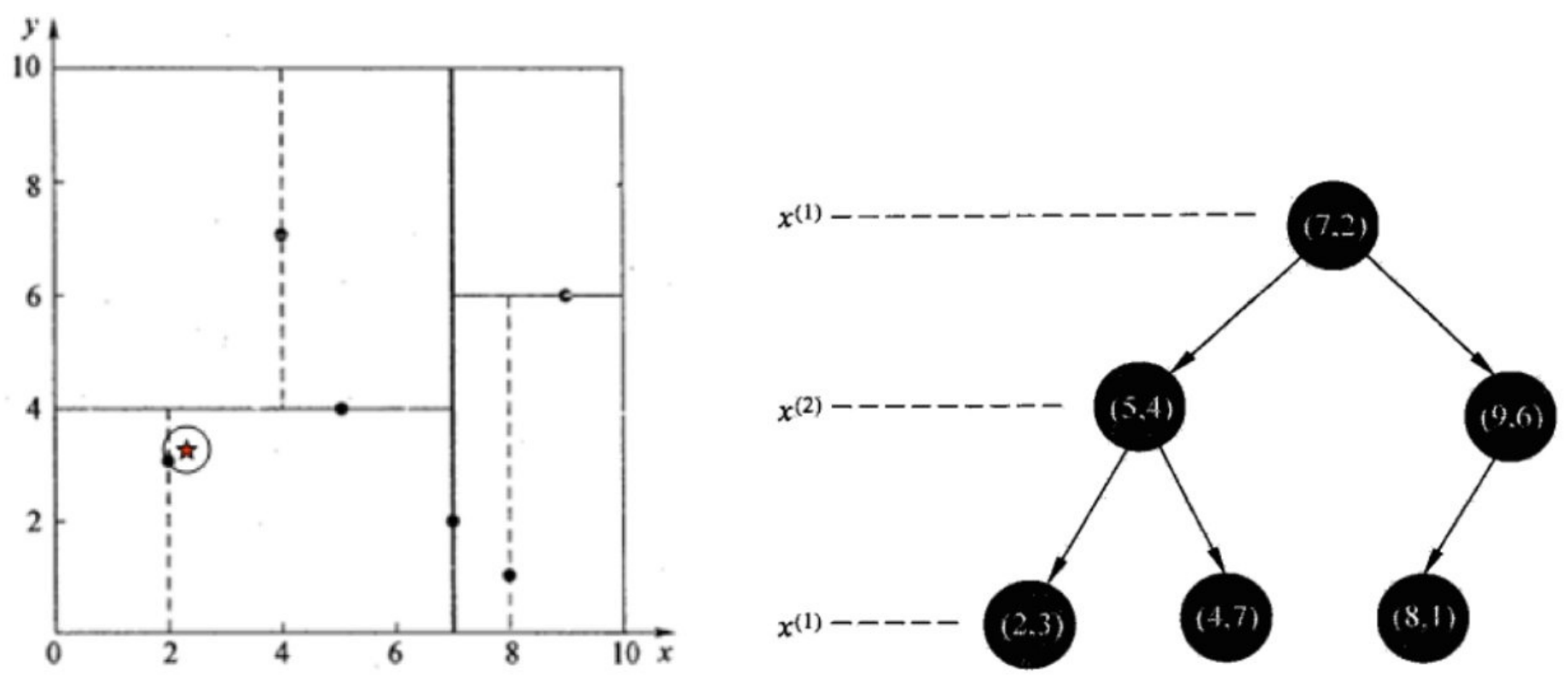
在(7,2)点测试到达(5,4)，在(5,4)点测试到达(2,3)，然后search_path中的结点为<(7,2),(5,4), (2,3)>，从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141；

然后回溯⾄(5,4)，以(2.1,3.1)为圆⼼，以dist=0.141为半径画⼀个圆，并不和超平⾯y=4相交，如上图，所以不必跳到结点(5,4)的右⼦空间去搜索，因为右⼦空间中不可能有更近样本点了。

于是再回溯⾄(7,2)，同理，以(2.1,3.1)为圆⼼，以dist=0.141为半径画⼀个圆并不和超平⾯x=7相交，所以也不⽤跳到结点(7,2)的右⼦空间去搜索。

⾄此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2.1,3.1)的最近邻点，最近距离为0.141。

查找点(2,4.5)

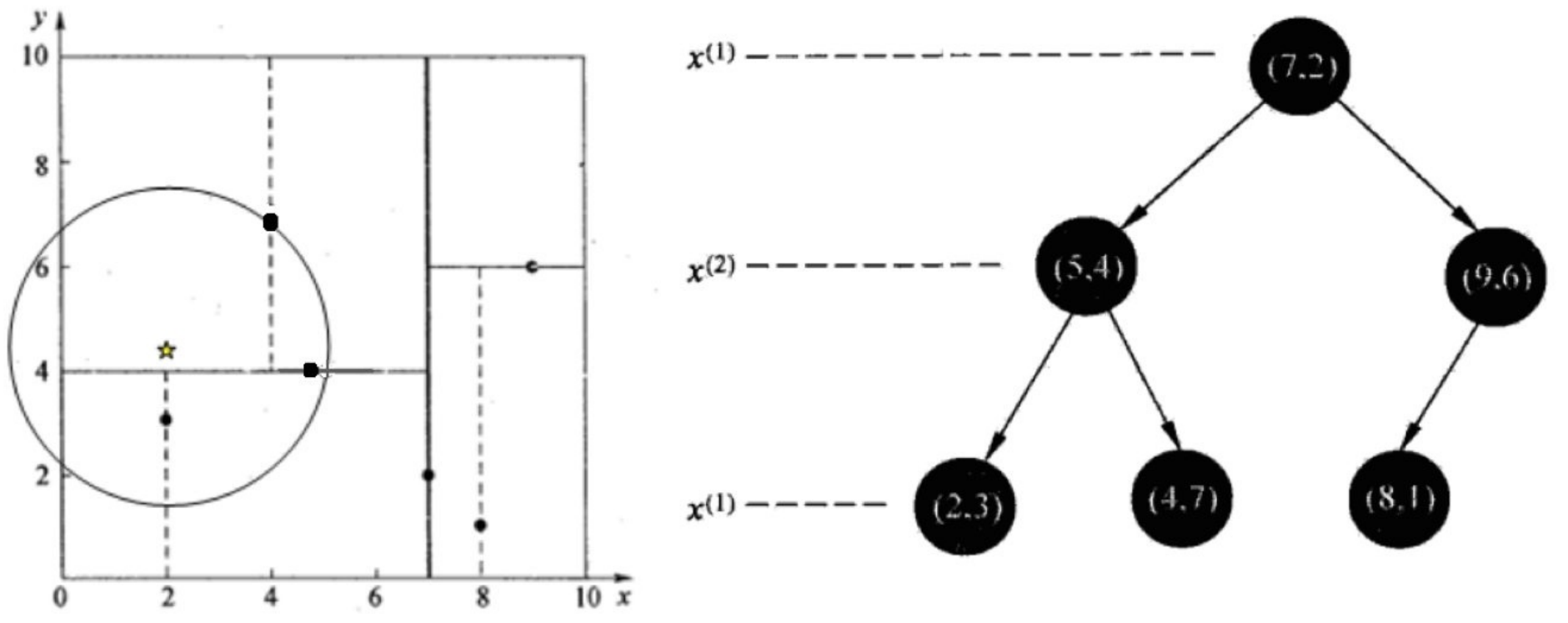
在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)【优先选择在本域搜索】，然后search_path中的结点为<(7,2),(5,4),(4,7)>，从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202；

然后回溯⾄(5,4)，以(2,4.5)为圆⼼，以dist=3.202为半径画⼀个圆与超平⾯y=4相交，所以需要跳到(5,4)的左⼦空间去搜索。所以要将(2,3)加⼊到search_path中，现在search_path中的结点为<(7,2),(2, 3)>；另外，(5,4)与(2,4.5)的距离为3.04 < dist = 3.202，所以将(5,4)赋给nearest，并且dist=3.04。

回溯⾄(2,3)，(2,3)是叶⼦节点，直接判断(2,3)是否离(2,4.5)更近，计算得到距离为1.5，所以nearest更新为(2,3)，dist更新为(1.5)，回溯⾄(7,2)，同理，以(2,4.5)为圆⼼，以dist=1.5为半径画⼀个圆并不和超平⾯x=7相交, 所以不⽤跳到结点(7,2)的右⼦空间去搜索。

⾄此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2,4.5)的最近邻点，最近距离为1.5。

总结

kd树的构建过程【知道】
- 1.构造根节点
- 2.通过递归的⽅法，不断地对k维空间进⾏切分，⽣成⼦节点
- 3.重复第⼆步骤，直到⼦区域中没有实例时终⽌
- 需要关注细节：a.选择向量的哪⼀维进⾏划分；b.如何划分数据
kd树的搜索过程【知道】
- 1.⼆叉树搜索⽐较待查询节点和分裂节点的分裂维的值，（⼩于等于就进⼊左⼦树分⽀，⼤于就进⼊右⼦树分⽀直到叶⼦结点）
- 2.顺着“搜索路径”找到最近邻的近似点
- 3.回溯搜索路径，并判断搜索路径上的结点的其他⼦结点空间中是否可能有距离查询点更近的数据点，如果有可能，则需要跳到其他⼦结点空间中去搜索
- 4.重复这个过程直到搜索路径为空

数据加载与分布查看

通过创建⼀些图，以查看不同类别是如何通过特征来区分的。

在理想情况下，标签类将由⼀个或多个特征对完美分隔。在现实世界中，这种理想情况很少会发⽣。

seaborn介绍

(系统学习参照：《8-seaborn高级绘图工具》）

Seaborn 是基于 Matplotlib 核⼼库进⾏了更⾼级的 API 封装，可以让你轻松地画出更漂亮的图形。⽽ Seaborn的漂亮主要体现在配⾊更加舒服、以及图形元素的样式更加细腻。
安装 pip install seaborn
seaborn.lmplot() 是⼀个⾮常有⽤的⽅法，它会在绘制⼆维散点图时，⾃动完成回归拟合
- sns.lmplot() ⾥的 x, y 分别代表横纵坐标的列名,
- data= 是关联到数据集,
- hue=*代表按照 species即花的类别分类显示,
- fit_reg=是否进⾏线性拟合。

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd

# %matplotlib inline
# 获取数据
iris = load_iris()
# 加工数据为DataFrame类型
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['target'] = iris.target
sns.lmplot(x='sepal width (cm)', y='sepal length (cm)', hue='target', data=df)
plt.xlabel('sepal width (cm)')
plt.ylabel('sepal length (cm)')
plt.title('鸢尾花花瓣长度和宽度关系图')
plt.tight_layout()
plt.show()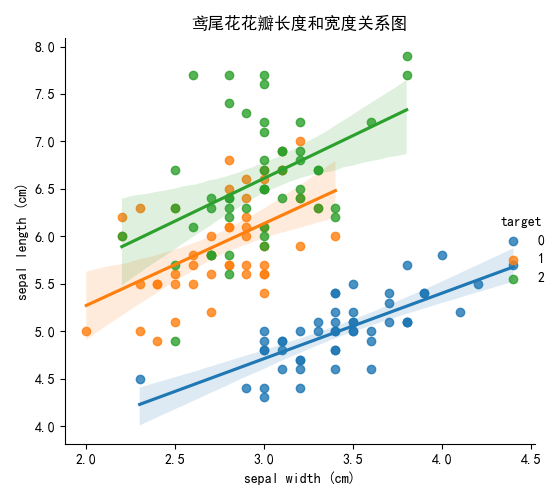

k近邻算法api

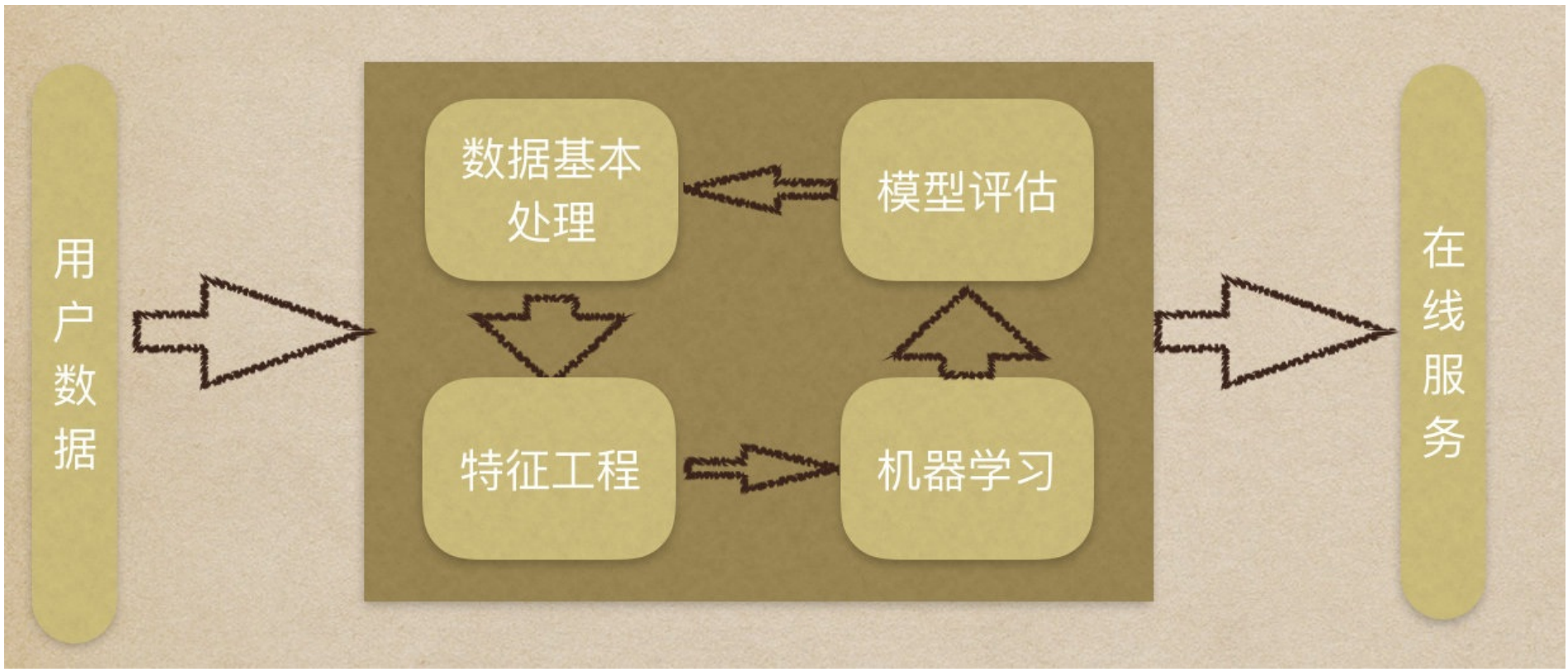
机器学习流程复习：

1.获取数据集

2.数据基本处理

3.特征⼯程

4.机器学习

5.模型评估

API介绍

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')
- n_neighbors：
  - int,可选（默认= 5），k_neighbors查询默认使⽤的邻居数
- algorithm：{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}
  - 快速k近邻搜索算法，默认参数为auto，可以理解为算法⾃⼰决定合适的搜索算法。除此之外，⽤户也可以⾃⼰指定搜索算法ball_tree、kd_tree、brute⽅法进⾏搜索。
  - brute是蛮⼒搜索，也就是线性扫描，当训练集很⼤时，计算⾮常耗时。
  - kd_tree，构造kd树存储数据以便对其进⾏快速检索的树形数据结构，kd树也就是数据结构中的⼆叉树。以中值切分构造的树，每个结点是⼀个超矩形，在维数⼩于20时效率⾼。
  - ball tree是为了克服kd树⾼维失效⽽发明的，其构造过程是以质⼼C和半径r分割样本空间，每个节点是⼀个超球体。

案例：鸢尾花种类预测

数据集介绍（略，见上文）

步骤分析：

1.获取数据集

2.数据基本处理

3.特征⼯程

4.机器学习(模型训练)

5.模型评估

代码过程

导⼊模块

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

先从sklearn当中获取数据集，然后进⾏数据集的分割

# 1，导入sklearn小数据集
iris=load_iris()
# 2，数据拆分为：训练集特征值、测试集特征值、训练集⽬标值、测试集⽬标值
train_data,test_data,train_target,test_target = train_test_split(iris.data,iris.target, test_size=0.2,random_state=22)
#data_train, data_test, target_train, target_test

进⾏数据标准化
- 特征值的标准化

# 3，特征工程-标准化
scaler = StandardScaler()
transform_train_data = scaler.fit_transform(train_data)
transform_test_data = scaler.transform(test_data)

模型进⾏训练预测

# 4，（机器学习）模型训练
estimator = KNeighborsClassifier(n_neighbors=3)
estimator.fit(transform_train_data, train_target)
# 5，模型评估
# 方法1：比较预测标签和真实标签
predict_target = estimator.predict(transform_test_data)
print("预测结果为:\n", predict_target)
print('⽐对真实值和预测值：\n',predict_target==test_target)
# 方法2：直接计算准确率
score = estimator.score(transform_test_data, test_target)
print('模型预测准确率为:', score)

查看打印结果

 预测结果为:
 [1 0 0 2 2 2 0 2 0 2 2 0 1 1 1 1 1 2 2 0 2 1 0 1 2 1 0 0 2 1]
⽐对真实值和预测值：
 [ True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True False]
模型预测准确率为: 0.9666666666666667

案例⼩结

在本案例中，具体完成内容有：

使⽤可视化加载和探索数据，以确定特征是否能将不同类别分开。
通过标准化数字特征并随机抽样到训练集和测试集来准备数据。
通过统计学，精确度度量进⾏构建和评估机器学习模型。

KNN算法总结

优点

简单有效
重新训练的代价低
适合类域交叉样本
- KNN⽅法主要靠周围有限的邻近的样本,⽽不是靠判别类域的⽅法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN⽅法较其他⽅法更为适合。
适合⼤样本⾃动分类
- 该算法⽐较适⽤于样本容量⽐较⼤的类域的⾃动分类，⽽那些样本容量较⼩的类域采⽤这种算法⽐较容易产⽣误分。

缺点

惰性学习
- KNN算法是懒散学习⽅法（lazy learning,基本上不学习），⼀些积极学习的算法要快很多
类别评分不是规格化
- 不像⼀些通过概率评分的分类
输出可解释性不强
- 例如决策树的输出可解释性就较强
对不均衡的样本不擅⻓
- 当样本不平衡时，如⼀个类的样本容量很⼤，⽽其他类样本容量很⼩时，有可能导致当输⼊⼀个新样本时，该样本的K个邻居中⼤容量类的样本占多数。可以采⽤权值的⽅法（和该样本距离⼩的邻居权值⼤）来改进。
计算量较⼤
- ⽬前常⽤的解决⽅法是事先对已知样本点进⾏剪辑，事先去除对分类作⽤不⼤的样本。

案例：预测用户最想去哪个地方打卡(Facebook)

本次比赛的目标是预测用户最想去哪个地方打卡。为了达到此目的，Facebook 创建了一个虚拟世界，其中包含位于 10 公里 x 10 公里方圆内的超过 10 万个地点。你的任务是针对给定的一组坐标，返回最有可能出现地点的排序列表。数据被伪造以模拟来自移动设备的位置信号，让你体会到处理由不准确和噪声值组成的复杂真实数据需要什么。不一致和错误的位置数据可能会影响 Facebook 打卡等服务的体验。

kaggke官方地址：https://www.kaggle.com/c/facebook-v-predicting-check-ins

数据集介绍

数据介绍：

⽂件说明 train.csv, test.csv
row id：签⼊事件的id
x y：坐标
accuracy: 准确度，定位精度
time: 时间戳
place_id: 签到的位置，这也是你需要预测的内容

步骤分析

对于数据做⼀些基本处理（这⾥所做的⼀些处理不⼀定达到很好的效果，我们只是简单尝试，有些特征我们可以根据⼀些特征选择的⽅式去做处理）
- 1 缩⼩数据集范围 DataFrame.query()
- 2 选取有⽤的时间特征
- 3 将签到位置少于n个⽤户的删除
分割数据集
标准化处理
k-近邻预测

具体步骤：

# 1.获取数据集
# 2.基本数据处理
# 2.1 缩⼩数据范围
# 2.2 选择时间特征
# 2.3 去掉签到较少的地⽅
# 2.4 确定特征值和⽬标值
# 2.5 分割数据集
# 3.特征⼯程 -- 特征预处理(标准化)
# 4.机器学习 -- knn+cv
# 5.模型评估

代码实现

import pandas as pd
from sklearn.model_selection import train_test_split,GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
import numpy as np

1.获取数据集

# 1，读取数据
data=pd.read_csv(r'D:\learn\000人工智能数据大全\黑马数据\科学计算数据\FBlocation_FaceBook\train.csv')

2.基本数据处理

# 2，数据量级缩减（原数据29118021条，太庞大，本地电脑处理太耗时）
# 2.1数据缩减
# 由于原来的地图面积是十公里，太大，我们计划仅仅取出其中一部分区域进行预测
# 查看位置x和y的最大最小值：x最大值是:10.0,x最小值是:0.0,y最大值是:10.0,y最小值是:0.0
# print(f'x最大值是:{data['x'].max()},x最小值是:{data['x'].min()},y最大值是:{data['y'].max()},y最小值是:{data['y'].min()}')
part_data=data.query('6>x>=5 & 6>y>=5')
print(part_data.shape)#(298762, 6)
part_data.head()
# 2.2，删除打卡地点极少的部分数据
# 查看不同地点打卡总数量排序(打印结果看出：总共Length: 6987个打卡地点，其中单个地点最多打卡1601，最少打卡1次
location_sort=part_data.groupby('place_id').size().sort_values(ascending=False)
#删除总打卡次数少于50的地点对应的数据
good_location_id=location_sort[location_sort>=50].index
part_data=part_data[part_data['place_id'].isin(good_location_id)]
part_data.shape#(268266, 6)相比之前少量三万低频数据
# 3.1，数据特征构造
# 原数据time特征是时间戳，我们可以将其拆解成年月日时分秒，以及星期几，从而更细力度的估算出某人何时会出现在何地
time=pd.to_datetime(part_data['time'],unit='s')# unit='s':以秒为单位，1970-01-06 22:11:05，从拆分后的数据我们可以看出，时间数据是被脱敏过的，1970年根本没有facebook
# 上一步输出的结果是Series，还需要DatetimeIndex进一步处理,才能城区
time=pd.DatetimeIndex(time)
part_data['day']=time.day
part_data['hour']=time.hour
part_data['weekday']=time.weekday
part_data.head()
# 3.2,确定特征值和⽬标值
feature_data=part_data[['x','y','day','hour','weekday','accuracy']]
target_data=part_data['place_id']
# 3.3，数据拆分（训练集，测试集）
train_feature_data,test_feature_data,train_target_data,test_target_data=train_test_split(feature_data,target_data,test_size=0.2,random_state=66)

3.特征⼯程--特征预处理(标准化）

# 3.4数据标准化
scaler=StandardScaler()
train_feature_data=scaler.fit_transform(train_feature_data)
test_feature_data=scaler.transform(test_feature_data)

4.机器学习--knn+cv

# 4，模型训练
# 4.1 实例化⼀个估计器
estimator=KNeighborsClassifier()
# 4.2配置交叉验证与模型搜索
param_grid={'n_neighbors':[3,5,7]}
estimator=GridSearchCV(estimator=estimator,param_grid=param_grid,cv=5)
# 4.3模型训练
estimator.fit(train_feature_data,train_target_data)

5.模型评估

#基本评估⽅式
score=estimator.score(test_feature_data,test_target_data)
print("模型预测准确率为：\n",score)
predict=estimator.predict(test_feature_data)
print("模型预测打卡地点列表为：\n",predict)
print("模型预测打卡地点正确与否：\n",predict==test_target_data)

查看打印结果

 模型预测准确率为：
 0.3477653110672084
模型预测打卡地点列表为：
 [6733590547 6358374233 8241900545 ... 8202183657 7994946702 9443429045]
模型预测打卡地点正确与否：
 6846311     False
3063932     False
21749847    False
22575416    False
27608774    False
            ...  
12413690     True
6210785     False
1586015      True
11334483     True
13573608    False
Name: place_id, Length: 53654, dtype: bool

#使⽤交叉验证后的评估⽅式
# 模型评估详细数据查看
print("最好的模型为：\n",estimator.best_estimator_)
print("模型最高得分为：\n",estimator.best_score_)
print("模型最佳参数是：\n",estimator.best_params_)
print("每次交叉验证模型表现详细数据：\n",estimator.cv_results_)

查看打印结果

 最好的模型为：
 KNeighborsClassifier()
模型最高得分为：
 0.32793600079050733
模型最佳参数是：
 {'n_neighbors': 5}
每次交叉验证模型表现详细数据：
 {'mean_fit_time': array([0.3677681 , 0.37499261, 0.37294168]), 'std_fit_time': array([0.02292145, 0.02539998, 0.01680919]), 'mean_score_time': array([2.62927237, 2.84603481, 2.9562346 ]), 'std_score_time': array([0.03522549, 0.1438885 , 0.05341459]), 'param_n_neighbors': masked_array(data=[3, 5, 7],
             mask=[False, False, False],
       fill_value=999999), 'params': [{'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}], 'split0_test_score': array([0.31940917, 0.32350954, 0.31817441]), 'split1_test_score': array([0.32595578, 0.33136081, 0.32437155]), 'split2_test_score': array([0.32277154, 0.32719817, 0.32158334]), 'split3_test_score': array([0.32139695, 0.32938819, 0.3232608 ]), 'split4_test_score': array([0.32314431, 0.32822329, 0.32300452]), 'mean_test_score': array([0.32253555, 0.327936  , 0.32207892]), 'std_test_score': array([0.00215383, 0.00260993, 0.00214479]), 'rank_test_score': array([2, 1, 3])}

cv_results = estimator.cv_results_
for i in range(len(cv_results['params'])):
    print(f"参数：{cv_results['params'][i]}, 平均分：{cv_results['mean_test_score'][i]}")

参数：{'n_neighbors': 2}, 平均分：0.32407840793341296
参数：{'n_neighbors': 4}, 平均分：0.31396398828980905
参数：{'n_neighbors': 6}, 平均分：0.31045102361282282

posted @ 2025-04-28 20:46 指尖下的世界阅读(188) 评论(0) 收藏举报

刷新页面返回顶部

指尖下的世界

今日事今日毕,今日无事早休息.

K近邻算法(KNN)：机器学习入门必学算法

1 什么是K-近邻算法

最近邻域搜索（Nearest-Neighbor Lookup）

K-近邻算法(KNN)概念

电影类型分析

KNN算法流程总结

近邻算法的原理及scikit-learn-API介绍

核心概念​

scikit-learn-API(分类器​)​

参数选择与影响​

权重机制​​

优缺点对比​​

​​ 应用场景​​

关键总结​​

距离度量

kd树

简介

原理

构造步骤

选点与切分

维度选择

案例分析

树的建⽴

回溯

查找点(2.1,3.1)

查找点(2,4.5)

数据加载与分布查看

seaborn介绍

k近邻算法api

API介绍

案例：鸢尾花种类预测

KNN算法总结

优点

缺点

案例：预测用户最想去哪个地方打卡(Facebook)

数据集介绍

步骤分析

代码实现

核心概念

scikit-learn-API(分类器)

参数选择与影响

权重机制

优缺点对比

应用场景

关键总结