5-NumPy
NumPy历史
- 1995年Jim HugUNin开发了Numeric
- 随后Numarray包诞生
- Travis Oliphants整合Numeric和Numarray,开发NumPy,2006年第一个版本诞生
- 使用Anaconda发行版的Python,已经安装好NumPy模块,所以可以不用再安装NumPy模块了。
- 依照标准的NumPy标准,习惯使用import numpy as np的方式导入该模块。
NumPy简介
NumPy:Numerical Python,即数值Python包,是Python进行科学计算的一个基础包,用于快速处理任意维度的数组。一定需要先掌握该包的主要使用方式。
Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务,使用Numpy比直接使用Python要简洁的多。
Numpy使用ndarray对象来处理多维数组,该对象是一个快速而灵活的大数据容器。
官方文档:https://docs.scipy.org/doc/numpy/user/index.html
NumPy模块是Python的一种开源的数值计算扩展,是一个用python实现的科学计算包,主要包括:
- ndarray(N-dimensional array object):一个具有矢量算术运算和复杂广播能力的快速且节省空间的多维数组
- ufunc(universal function object):用于对整组数据进行快速运算的标准数学函数
- 实用的线性代数、傅里叶变换和随机数生成函数。
NumPy和稀疏矩阵的运算包Scipy配合使用更加方便。
ndarray介绍
NumPy的数组类被称作ndarray,它是numpy的核心数据结构。通常被称作数组(或多维数组)。
NumPy provides an N-dimensional array type, the ndarray,which describes a collection of “items” of the same type.
注意numpy.array和标准Python库类array.array并不相同,后者只处理一维数组和提供少量功能。
| 特性 | Python 列表 | NumPy 数组 |
|---|---|---|
| 元素类型 | 可以混合不同类型(如 [1, "a"]) |
所有元素必须类型相同 |
| 内存存储 | 非连续存储 | 连续存储,支持高效计算 |
| 动态扩展性 | 支持动态增删元素(如 append()) |
元素数量固定,不可直接修改 |
元素的数据类型由dtype(data-type)对象来指定,每个ndarray只有一种dtype类型。
ndarray的大小固定,创建好数组后数组大小是不会再发生改变的
提问:使用Python列表可以存储一维数组,通过列表的嵌套可以实现多维数组,那么为什么还需要使用Numpy的ndarray呢?
ndarray与Python原生list运算效率对比
import random import numpy as np # 构建普通数组 list=[] for i in range(100000000): list.append(random.random()) #构建多维数组 arr=np.array(list) # 魔法命令统计传统数组求和耗时 %time sum1=sum(list) # 统计多维数组求和耗时 %time sum2=np.sum(arr) print(sum1,sum2)
CPU times: user 852 ms, sys: 262 ms, total: 1.11 sWall time: 1.13 sCPU times: user 133 ms, sys: 653 µs, total: 133 msWall time: 134 ms
思考:ndarray为什么可以这么快?
ndarray的内存块风格

小结
- 内存块风格
-
- list -- 分离式存储,存储内容多样化
- ndarray -- 一体式存储,存储类型必须一样
- ndarray支持并行化运算(向量化运算)
- ndarray底层是用C语言写的,效率更高,释放了GIL
创建ndarray多维数组的函数
可以通过numpy模块中的常用的几个函数进行创建ndarray多维数组对象,主要函数如下:
- array函数:接收一个普通的python序列,并将其转换为ndarray
- zeros函数:创建指定长度或者形状的全零数组。
- ones函数:创建指定长度或者形状的全1数组。
- empty函数:创建一个没有任何具体值的数组(准确地说是创建一些未初始化的ndarray多维数组)
帮助文档
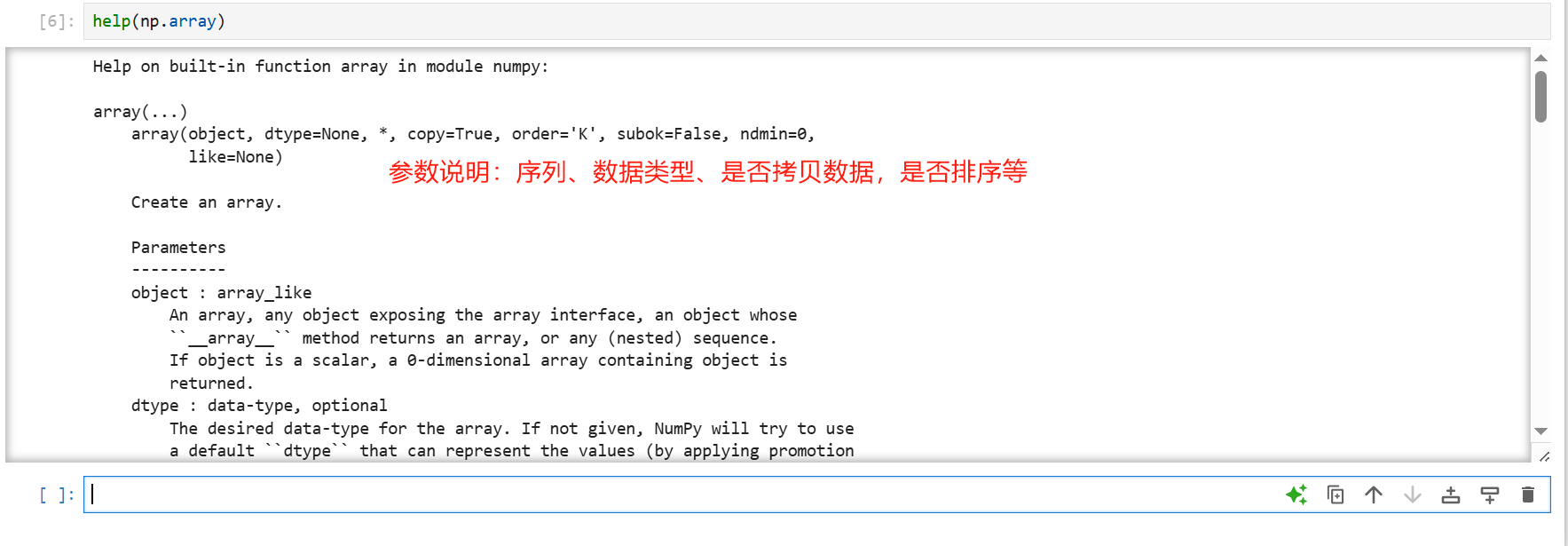
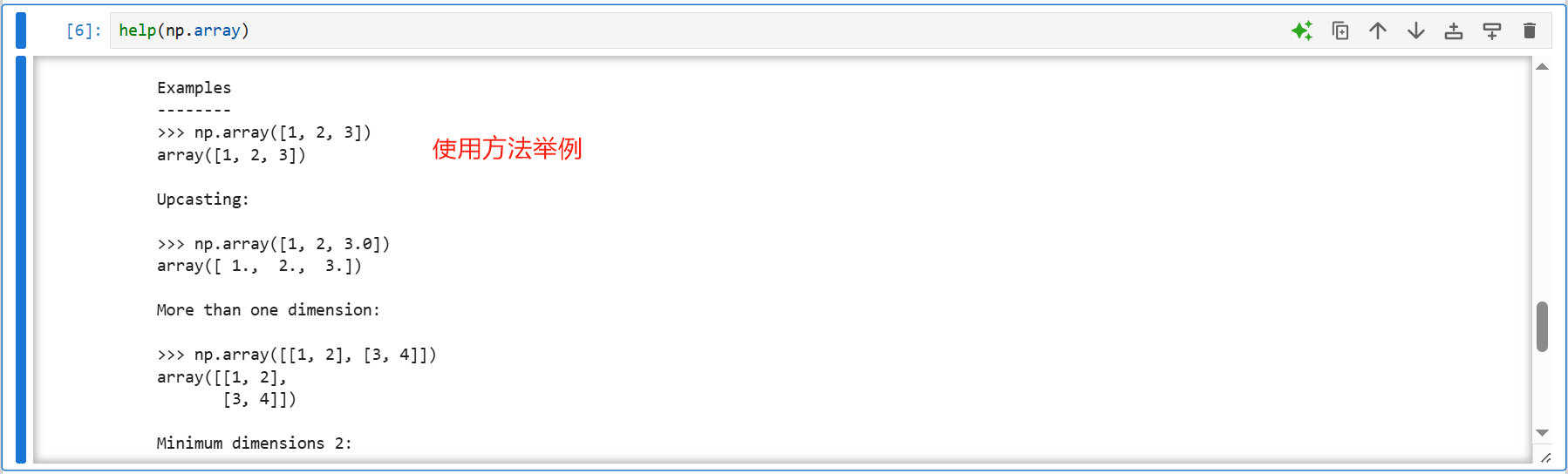
array函数
array函数:接收一个普通的python序列或者ndarray,并将其转换为ndarray

从现有数组生成
a = np.array([[1,2,3],[4,5,6]]) # 从现有的数组当中创建 a1 = np.array(a)#深拷贝 # 相当于索引的形式,并没有真正的创建一个新的,修改会影响原数组 a2 = np.asarray(a)#浅拷贝

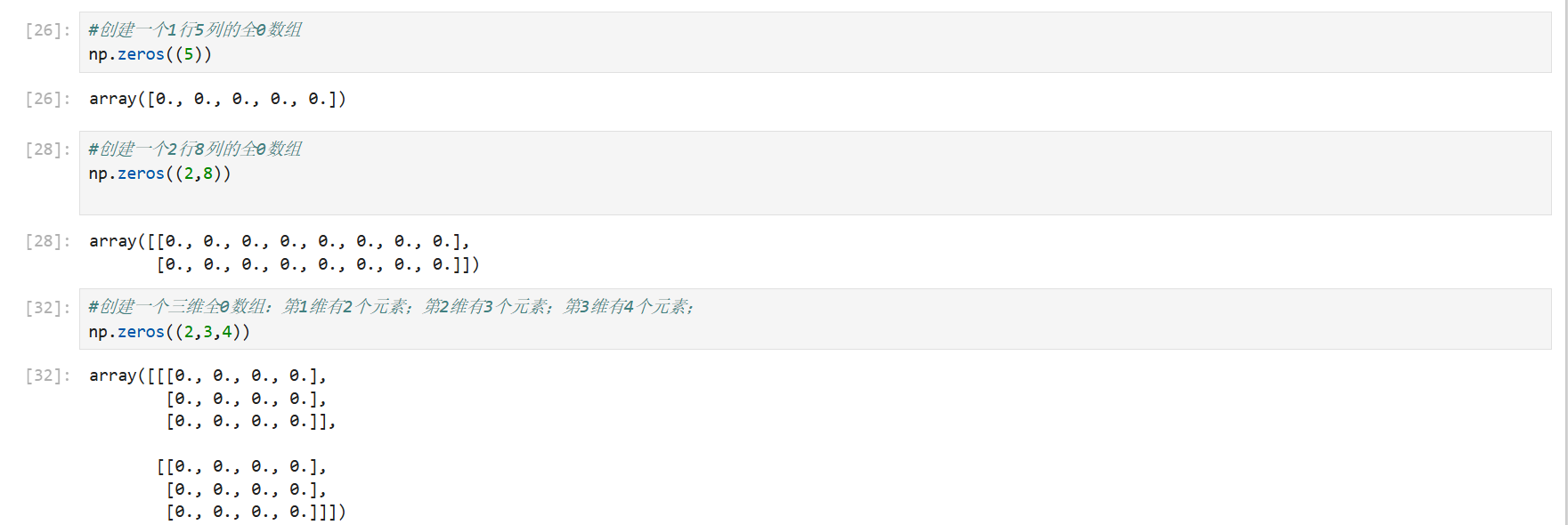
zeros函数
zeros函数:创建指定长度或者形状的全0数组。
np.zeros(5) np.zeros([5,5]) np.zeros((5,5))
ones函数
ones函数:创建指定长度或者形状的全1数组。

0和1数组其他创建方法
np.ones(shape, dtype)np.ones_like(a, dtype)np.zeros(shape, dtype)np.zeros_like(a, dtype)
ones = np.ones([4,8])
ones
array([[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.]])np.zeros_like(ones)
array([[0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0.]])empty函数
empty函数:创建一个没有任何具体值的数组(准确地说是创建一些未初始化的ndarray多维数组)
np.empty((5,5))
array([[1.25318603e-311, 1.25318814e-311, 9.18225940e-072,1.25304780e-311, 1.25304780e-311],
[1.25304780e-311, 1.25304771e-311, 1.25304771e-311,1.25304771e-311, 1.25304999e-311],
[1.25304991e-311, 1.25304991e-311, 1.25305004e-311,1.25305009e-311, 1.25305004e-311],
[1.25305478e-311, 1.25305477e-311, 1.25306303e-311,1.25315601e-311, 1.25315598e-311],
[1.25315775e-311, 1.25315775e-311, 1.25315760e-311,1.25315869e-311, 1.25315932e-311]])如果你需要初始值为 1 的数组,应该使用np.ones();如果你只需要一块指定大小的内存空间(并且会立即覆盖其中的值),可以使用np.empty()以获得更好的性能。
生成固定范围的数组
arange(start,stop, step, dtype)
- 参数:
-
- step:步长,默认值为1
注意:最终创建的数组不包含终值
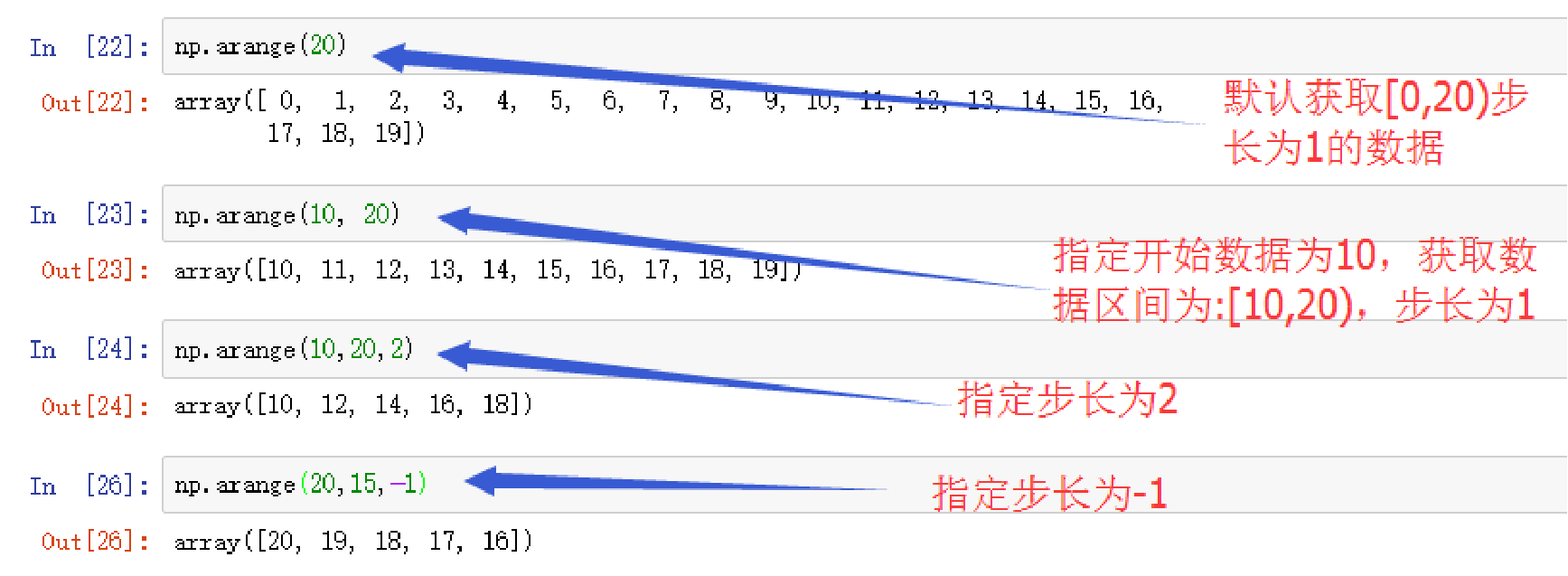
linspace(start, stop, num, endpoint)
- 参数:
-
- start:序列的起始值
- stop:序列的终止值
- num:要生成的等间隔样例数量,默认为50
- endpoint:序列中是否包含终值,默认为ture
#help说明: linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0) Return evenly spaced numbers over a specified interval.

# 生成等间隔的数组 np.linspace(0, 100, 11) 返回结果: array([ 0., 10., 20., 30., 40., 50., 60., 70., 80., 90., 100.])
注:需要生成连续数据,绘制平滑函数图像时,特别有用
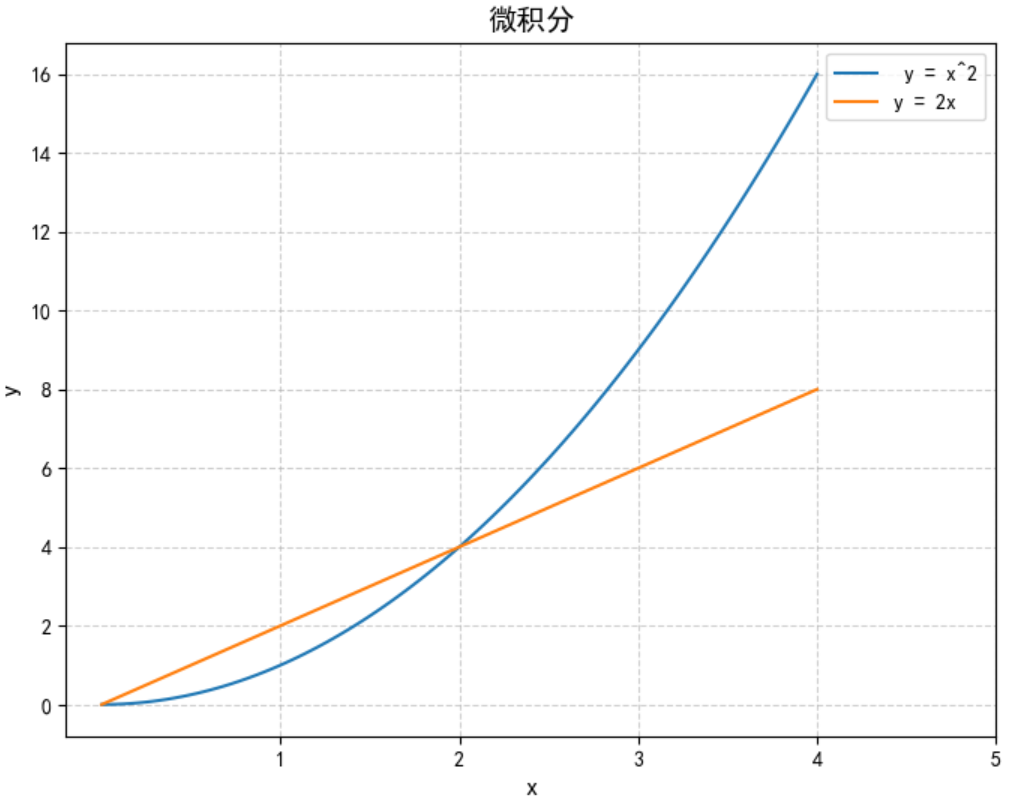
logspace(start,stop, num)
和linspace函数类似,不过创建的是等比数列数组
logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None, axis=0)
Return numbers spaced evenly on a log scale.

生成随机数组
使用模块介绍np.random模块
正态分布随机数组
关于正态分布的知识请移步数学和统计学基础概念了解。
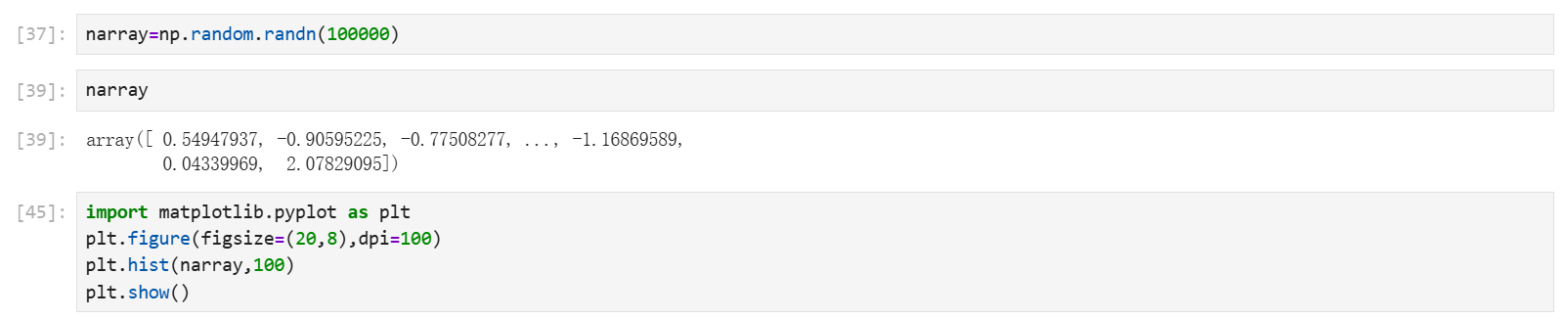
np.random.randn(d0, d1, …, dn)
numpy.random.randn 是 NumPy 中用于生成服从 标准正态分布(均值为 0,标准差为 1) 的随机数数组的函数。它广泛用于模拟正态分布数据、初始化神经网络权重、统计分析等场景。

应用场景
-
模拟数据:
# 模拟 100 个正态分布的样本 samples = np.random.randn(100)
-
机器学习初始化:
# 初始化神经网络权重(均值为 0,标准差为 1) weights = np.random.randn(64, 32) # 64x32 的权重矩阵
-
统计分析:
# 生成两组正态分布数据,进行 t 检验 group1 = np.random.randn(50) group2 = np.random.randn(50) + 0.5 # 均值偏移 0.5 from scipy.stats import ttest_ind t_stat, p_value = ttest_ind(group1, group2)
-
生成非标准正态分布:
若需生成均值为μ、标准差为σ的正态分布,可基于randn转换:μ, σ = 5, 2 data = μ + σ * np.random.randn(100) # 均值为 5,标准差为 2
np.random.normal(loc=0.0, scale=1.0, size=None)
loc:float
- 此概率分布的均值(对应着整个分布的中心centre)
scale:float
- 此概率分布的标准差(对应于分布的宽度,scale越大越矮胖,scale越小,越瘦高)
size:int or tuple of ints
- 输出的shape,默认为None,只输出一个值
normalarr=np.random.normal(1,5,100000000) plt.hist(normalarr,1000) plt.axvline(x=1, color='red', linestyle='--')#生成竖线 plt.show()

- 随机生成涨跌幅在某个正态分布内,比如均值0,方差1
# 创建符合正态分布的4只股票5天的涨跌幅数据 stock_change = np.random.normal(0, 1, (4, 5)) stock_change
array([[ 0.0476585 , 0.32421568, 1.50062162, 0.48230497, -0.59998822],[-1.92160851, 2.20430374, -0.56996263, -1.44236548, 0.0165062 ],[-0.55710486, -0.18726488, -0.39972172, 0.08580347, -1.82842225],[-1.22384505, -0.33199305, 0.23308845, -1.20473702, -0.31753223]])
np.random.normal() 和 np.random.randn() 都是 NumPy 中生成正态分布随机数的函数,但它们在参数设置和默认行为上有显著区别。以下是详细对比:
1. 核心区别总结
| 特性 | np.random.normal() |
np.random.randn() |
|---|---|---|
| 分布参数 | 可自定义均值 (loc) 和标准差 (scale) |
固定为标准正态分布(均值=0,标准差=1) |
| 输入参数 | loc(均值), scale(标准差), size(输出形状) |
d0, d1, ..., dn(维度参数,直接指定形状) |
| 灵活性 | 高(支持任意均值和标准差) | 低(仅生成标准正态分布) |
| 接口设计 | 通用型函数 | 快捷函数(针对标准正态分布的简化版本) |
2. 函数参数对比
np.random.normal()
np.random.normal( loc=0.0, # 均值 (默认0) scale=1.0, # 标准差 (默认1) size=None # 输出形状 (默认单个值) )
np.random.randn()
np.random.randn( d0, d1, ..., dn # 维度参数(直接指定形状) )
3. 使用场景示例
场景 1:生成标准正态分布数据(均值为0,标准差为1)
np.random.normal()
data = np.random.normal(loc=0, scale=1, size=1000)
np.random.randn()更简洁
data = np.random.randn(1000) # 等效写法
场景 2:生成非标准正态分布数据(如均值=5,标准差=3)
仅能用 np.random.normal()
data = np.random.normal(loc=5, scale=3, size=1000)
场景 3:生成多维数组
np.random.normal()
data = np.random.normal(loc=0, scale=1, size=(2, 3)) # 2行3列
np.random.randn()
data = np.random.randn(2, 3) # 等效写法
np.random.standard_normal(size=None)
两者生成的随机数分布完全一致,底层实现也相同# randn 内部调用的是 standard_normal
arr=np.random.standard_normal(10000000) plt.hist(arr,1000) plt.show()

均匀分布随机数组
np.random.rand(d0,d1...dn)

np.random.rand(5,5)
-
与
randn的区别:-
np.random.rand:生成 [0,1) 均匀分布的随机数。 -
np.random.randn:生成 标准正态分布 的随机数。
-
验证是否均匀分布:
arr=np.random.rand(10000000) plt.hist(arr,1000) plt.show

np.random.random()
使用numpy.random中的random()函数来创建0-1之间的随机数元素,数组包含的元素数量由参数决定(np.random.random_sample的别名)

numpy.random.random() 和 numpy.random.rand() 功能完全相同,唯一区别在于参数传递方式,两者在性能和结果上无差异。
np.random.uniform(low=0.0, high=1.0, size=None)
- 功能:从一个均匀分布[low,high)中随机采样,注意定义域是左闭右开,即包含low,不包含high.
- 参数介绍:
- low: 采样下界,float类型,默认值为0;
- high: 采样上界,float类型,默认值为1;
- size: 输出样本数目,为int或元组(tuple)类型,例如,size=(m,n,k), 则输出mnk个样本,缺省时输出1个值。
- 返回值:ndarray类型,其形状和参数size中描述一致。
arr=np.random.uniform(1,10,5)#生成范围在1~10的随机数五个 arr
array([9.369543 , 4.81580831, 7.02010646, 4.96196996, 4.93288665])np.random.randint(low=0.0, high=1.0, size=None)
- 从一个均匀分布[low,high)中随机采样,注意定义域是左闭右开,即包含low,不包含high,生成一个整数或N维整数数组,
- 取数范围:若high不为None时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数。

np.random.choice(a, size=None, replace=True, p=None)
从给定的一维数组(或整数范围)中生成随机样本,支持以下特性:
- 均匀分布或自定义概率分布(通过
p参数)。 - 有放回抽样(
replace=True,默认)或无放回抽样(replace=False)。 - 灵活指定输出形状(
size参数)。
categories = np.random.choice(['A', 'B', 'C'], 50) print(categories )
['A' 'B' 'A' 'A' 'C' 'A' 'C' 'B' 'A' 'C' 'C' 'B' 'A' 'A' 'C' 'A' 'C' 'A'
'C' 'A' 'B' 'A' 'A' 'B' 'A' 'B' 'A' 'C' 'C' 'A' 'A' 'A' 'C' 'A' 'C' 'B'
'C' 'C' 'B' 'C' 'A' 'A' 'C' 'A' 'C' 'A' 'A' 'C' 'A' 'C']| 参数 | 类型 | 说明 |
|---|---|---|
a |
1D数组或整数 | 若为整数 n,等价于从 np.arange(n) 中抽样。 |
size |
整数或元组 | 输出形状,如 (2,3) 表示生成 2 行 3 列的数组。默认返回单个值。 |
replace |
布尔值 | True 表示有放回抽样(可重复抽取),False 表示无放回。 |
p |
1D数组(概率) | 每个元素的抽取概率,长度需与 a 一致,且概率和为 1。默认均匀分布。 |
应用场景
- 数据抽样:从数据集中随机选取训练/测试样本。
- 蒙特卡洛模拟:按概率分布生成随机事件。
- 增强随机性:在游戏或算法中生成随机选择。
固定随机种子
若需结果可复现,需设置随机种子:
np.random.seed(42) # 固定随机性 data = np.random.randn(3)
ndarray对象属性
ndim (ndim是“number of dimensions”的缩写)数组轴(维度)的个数,轴的个数被称作秩;就是告诉你这个数组是几维数组
shape 数组的维度, 例如一个2排3列的矩阵,它的shape属性将是(2,3),这个元组的长度显然是秩,即维度或者ndim属性
size 数组元素的总个数,等于shape属性中元组元素的乘积。
dtype 一个用来描述数组中元素类型的对象,可以通过创造或指定dtype使用标准Python类型。不过NumPy提供它自己的数据类型。
itemsize 数组中每个元素的字节大小。例如,一个元素类型为float64的数组itemsiz属性值为8(=64/8),又如,一个元素类型为complex32的数组itemsize属性为4(=32/8).

NumPy基本数据类型
数值型dtype的命名方式为:一个类型名称(eg:int、float等),后接一个表示各个元素位长的数字。
比如Python的float数据类型(双精度浮点值),需要占用8个字节(64位),因此在NumPy中记为float64。
每个数据类型都有一个类型代码,即简写方式。
|
数据类型 |
类型简写 |
说明 |
|
整数类型 |
||
|
int_ |
|
默认整形;整数默认类型为 |
|
intc |
|
等价于long的整形 |
|
int8 |
i1 |
字节整形,1个字节,范围:[-128,127] |
|
int16 |
i2 |
整形,2个字节,范围:[-32768,32767] |
|
int32 |
i3 |
整形,4个字节,范围:[-2^31, 2^31-1](-2147483648 到 2147483647) |
|
int64 |
i4 |
整形,8个字节,范围:[-2^63, 2^63-1] |
|
uint8 |
u1 |
8 位无符号整数, 1个字节, 范围:[0,255](0 到 255),常用于图像数据(像素值范围 0-255) |
|
uint16 |
u2 |
无符号整形, 2个字节, 范围:[0,65535] |
|
uint32 |
u3 |
无符号整形, 1个字节, 范围:[0, 2^32-1](0 到 4294967295) |
|
uint64 |
u4 |
无符号整形, 1个字节, 范围:[0,2^64-1] |
|
浮点类型(详参float数据类型详解) |
||
|
float_ |
|
float64简写形式;浮点数默认类型为 |
|
float16 |
f2 |
半精度浮点型(2字节):1符号位+5位指数+10位的小数部分 |
|
float32 |
f4或者f |
单精度浮点型(4字节):1符号位+8位指数+23位的小数部分(十进制有效数字:~6-7 位) |
|
float64 |
f8或者d |
双精度浮点型(8字节):1符号位+11位指数+52位的小数部分(十进制有效数字:~15-17 位) |
|
复数类型 |
||
|
complex_ |
c16 |
complex128的简写形式 |
|
complex64 |
c8 |
复数,由两个32位的浮点数来表示;由两个 |
|
complex128 |
c16 |
复数,由两个64位的浮点数来表示;由两个 |
|
布尔类型 |
||
| bool_ | b | 以一个字节形成存储的布尔值(True或者False) |
|
字符串类型 |
||
|
String_(str_) |
S |
固定长度的字符串类型(每个字符1个字节),比如:要创建一个长度为8的字符串,应该使用S8 |
|
Unicode_ |
U |
固定长度的unicode类型的字符串(每个字符占用字节数由平台决定),长度定义类似String_类型 固定长度字符串(例如 |
|
|
||
|
其他类型 |
||
| object | O | Python对象类型 |
| datetime64
|
M |
日期时间类型(支持年、月、日、小时等单位,如 用于时间序列分析(如 |
| timedelta64 | m | 时间间隔类型(与 datetime64 配合使用) |
创建numpy数组的时候可以通过属性dtype显式指定数据类型,如果不指定的情况下,numpy会自动推断出适合的数据类型,所以一般不需要显示给定数据类型。
NumPy数组基本操作
修改数组形状
ndarray.shape(new_shape)
通过shape()修改数组本身形状

ndarray.resize(new_shape)
ndarray.resize() 是原地修改数组形状和大小的方法,允许调整后的元素数量(总大小)与原数组不同。
- 扩展数组:新形状元素数更多时,填充
0(数值类型)或空值(对象类型)。 - 缩减数组:新形状元素数更少时,截断末尾元素(按内存顺序保留前面的元素)。
| 参数 | 类型 | 说明 |
|---|---|---|
new_shape |
元组/整数 | 新形状的维度。例如 (2,3) 或 2,3(非关键字参数形式)。 |
refcheck |
布尔值 | 默认 True:检查数组是否被其他对象引用。若存在引用,拒绝调整大小。 |


ndarray.resize() 和直接设置 ndarray.shape 都可以修改数组的形状,但它们在元素总数处理、内存操作和数据填充方式上有本质区别。
| 特性 | ndarray.resize(new_shape) |
ndarray.shape = new_shape |
|---|---|---|
| 元素总数是否可变 | ✅ 可以改变(自动填充或截断数据) | ❌ 必须与原数组元素总数一致,否则报错 |
| 是否原地操作 | ✅ 直接修改原数组 | ✅ 直接修改原数组 |
| 填充数据 | 填充 0(数值类型)或空值(对象类型) |
无填充,必须保持元素总数一致 |
| 适用场景 | 需要扩展或缩减数组大小 | 仅调整形状,不改变元素总数 |
ndarray.resize()与 np.resize() 函数的区别
| 特性 | ndarray.resize() |
np.resize() 函数 |
|---|---|---|
| 操作类型 | 原地修改原数组 | 返回新数组,原数组不变 |
| 填充行为 | 填充 0 或空值 |
重复原数据填充至新形状大小 |
| 适用场景 | 需要直接修改原数组 | 需保留原数组并生成新数组 |
ndarray.reshape(shape, order)






ndarray修改数据类型
ndarray.astype(type)
如果需要更改一个已经存在的数组的数据类型,可以通过astype方法进行修改从而得到一个新数组(原数组不变)。

ndarray.tobytes([order])
等价写法:ndarray.tostring([order]),不过ndarray.tostring([order])即将过期不建议使用
-
ndarray.tobytes()将数组的原始数据转换为 Python 的bytes对象,直接反映内存中的二进制内容。
| 参数 | 类型 | 可选值 | 说明 |
|---|---|---|---|
order |
字符串 | 'C', 'F', 'A' |
- 'C':按行优先(C 顺序)展开。- 'F':按列优先(Fortran 顺序)展开。- 'A':自动选择数组的连续顺序。 |
- 数据顺序:默认按 C 顺序(行优先) 展开,但可通过
order参数控制。 - 数据类型影响:字节序列的表示形式由数组的
dtype决定(例如int16占 2 字节,float32占 4 字节)。
x = np.array([[1, 2], [3, 4]], dtype='<u2') # 小端存储的 uint16 类型:每个字符占两个字节 bytes_c = x.tobytes(order='C')#行优先 print(bytes_c)
默认 C 顺序:

字节解析(每个元素占 2 字节,小端存储):
1→01 002→02 003→03 00- 4 →
04 00
内存展开顺序:逐行排列 → 0, 1, 2, 3。
Fortran 顺序:

字节解析:
- 按列优先展开:
1, 3, 2, 4→ 字节序列为01 00(1),03 00(3),02 00(2),04 00(4)。
与 tostring() 的兼容性
- 历史背景:
tobytes()替代了已弃用的tostring()方法,功能完全一致。 - 推荐使用:始终优先使用
tobytes()。
反向操作:np.frombuffer()
可将 bytes 数据重新转换为数组(需指定正确的 dtype 和 order):
# 从 bytes_c 恢复数组 restored = np.frombuffer(bytes_c, dtype='<u2').reshape(2, 2) print(restored) # 输出: # [[1 3] # [2 4]]
应用场景
- 二进制文件 I/O:将数组保存为二进制文件。
- 网络传输:序列化数组数据。
- 内存共享:与其他语言(如 C/C++)交互时传递原始内存数据。
IOPub data rate exceeded.The notebook server will temporarily stop sending outputto the client in order to avoid crashing it.To change this limit, set the config variable`--NotebookApp.iopub_data_rate_limit`.
jupyter notebook --generate-configvi ~/.jupyter/jupyter_notebook_config.py
## (bytes/sec) Maximum rate at which messages can be sent on iopub before they# are limited.c.NotebookApp.iopub_data_rate_limit = 10000000
数组与标量、数组之间的运算
数组不用循环即可对每个元素执行批量的算术运算操作,这个过程叫做矢量化,即用数组表达式代替循环的做法。
矢量化数组运算性能比纯Python方式快上一两个数据级。
大小相等的两个数组之间的任何算术运算都会将其运算应用到元素级上的操作。
元素级操作:在NumPy中,大小相等的数组之间的运算,为元素级运算,即只用于位置相同的元素之间,所得的运算结果组成一个新的数组,运算结果的位置跟操作数位置相同。

数组与标量运算
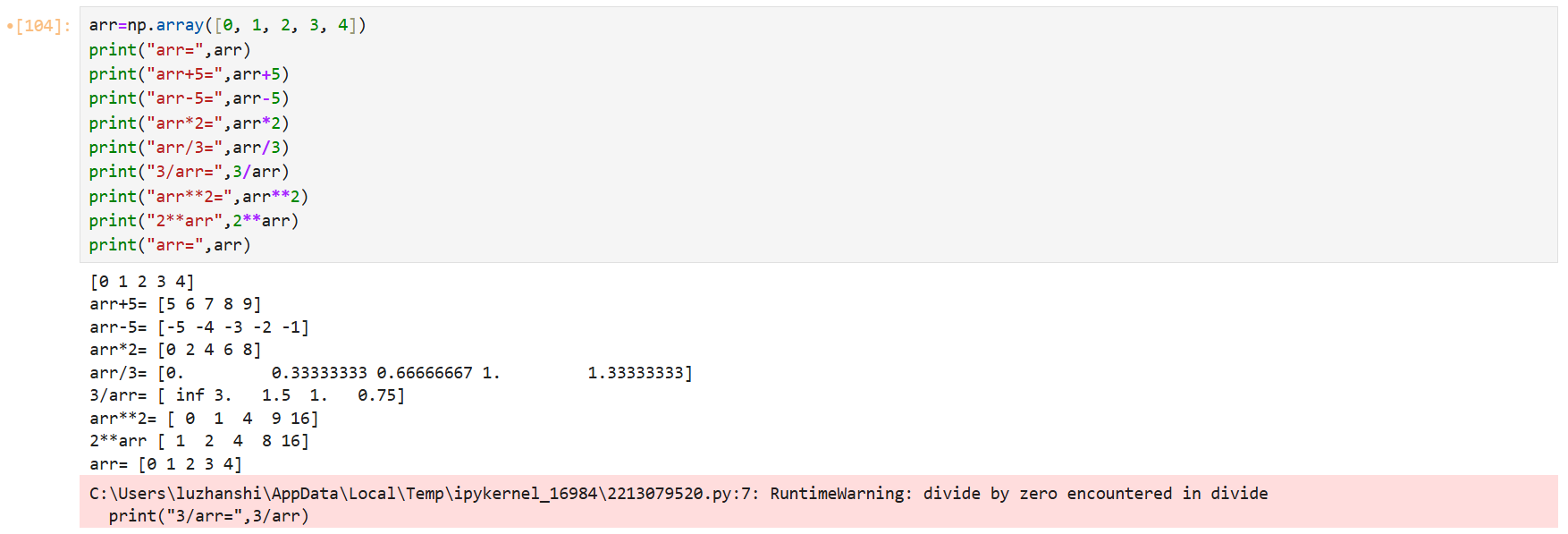
数组与数组运算

数组的矩阵积(matrix product)
矩阵积(matrix product):两个二维矩阵(行和列的矩阵)满足第一个矩阵的列数与第二个矩阵的行数相同,那么可以进行矩阵的乘法,即矩阵积,矩阵积不是元素级的运算。也称为点积、数量积。
一句话总结:矩阵积的结果数组的形状是(arr1的行数,arr2的列数)。
案例:根据学生的平时成绩(权重0.3)和期末成绩(权重0.7),求出最终成绩
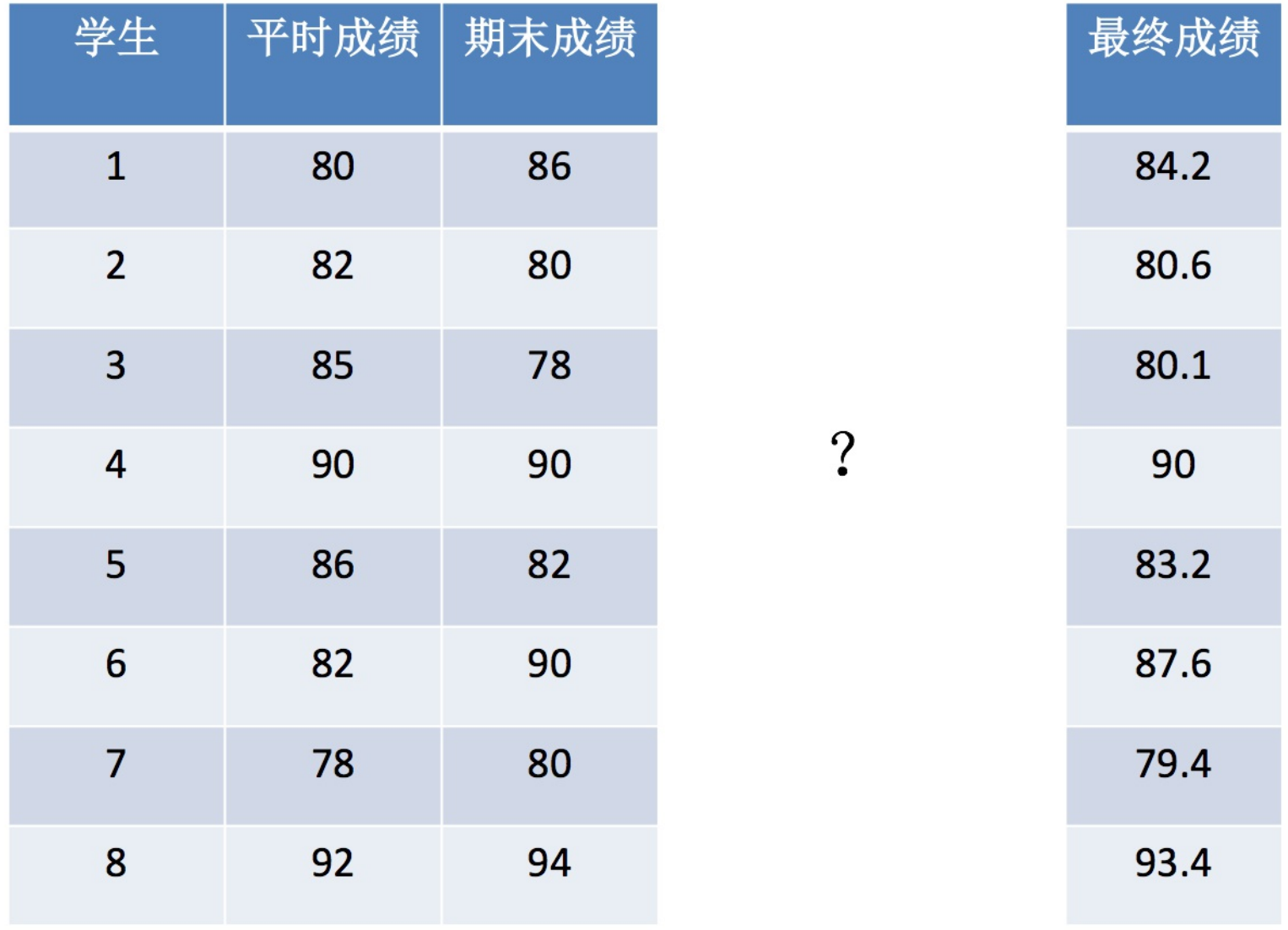
需求拆解:其实就是矩阵的乘法:

运算拆解=(80*0.3+86*0.7)+(82*0.3+80*0.7)+(85*0.3+78*0.7)+(...*0.3+...*0.7)
numpy.dot(arr1,arr2)

补充
np.dot(arr1, arr2) 并不仅限于二维数组的矩阵乘法。它是一个广义的点积函数,支持不同维度的数组运算,具体行为取决于输入数组的维度:1. 不同维度的行为总结
| 输入数组维度 | 运算规则 |
|---|---|
| 两个一维数组 | 计算向量内积(标量):所有对应元素乘积之和 |
| 一个二维 + 一个一维 | 矩阵与向量乘法,结果为一维数组 |
| 两个二维数组 | 标准矩阵乘法 |
| 高维数组(≥3维) | 执行张量收缩(沿特定轴的点积求和),结果维度由输入形状决定 |
具体示例
(1) 一维数组 → 标量内积
import numpy as np a = np.array([1, 2, 3]) b = np.array([4, 5, 6]) result = np.dot(a, b) # 1 * 4 + 2 * 5 + 3 * 6 = 32 print(result) # 输出: 32
二维数组与一维数组 → 矩阵乘向量(其实也是特殊的矩阵积:就好比把一维数组转成二维:(竖起来))
A = np.array([[1, 2], [3, 4]]) v = np.array([5, 6]) result = np.dot(A, v) # [1 * 5 + 2 * 6, 3 * 5 + 4 * 6] = [17, 39] print(result) # 输出: [17 39]
二维数组 → 矩阵乘法
A = np.array([[1, 2], [3, 4]]) B = np.array([[5, 6], [7, 8]]) result = np.dot(A, B) # 标准矩阵乘积 print(result) # 输出: # [[19 22] # [43 50]]
高维数组 → 张量收缩
A = np.arange(24).reshape(2, 3, 4) # 形状 (2, 3, 4) B = np.arange(24).reshape(2, 4, 3) # 形状 (2, 4, 3) result = np.dot(A, B) # 形状 (2, 3, 2, 3) # 计算逻辑:对 A 的最后一个轴(4)和 B 的倒数第二个轴(4)进行点积求和 # 输出维度为 (A.shape[0], A.shape[1], B.shape[0], B.shape[-1]) print(result.shape) # 输出: (2, 3, 2, 3)
与 @ 运算符和 np.matmul 的区别
| 函数/运算符 | 行为 |
|---|---|
np.dot |
支持广义点积(包括标量、矩阵、张量收缩) |
@ 或 np.matmul |
专为矩阵乘法设计,对高维数组执行广播矩阵乘法,不支持标量或某些维度收缩 |

# 高维数组使用 @ 运算符 A = np.arange(24).reshape(2, 3, 4) B = np.arange(24).reshape(2, 4, 3) result = A @ B # 形状 (2, 3, 3),执行批量矩阵乘法 print(result.shape) # 输出: (2, 3, 3)
总结
-
np.dot的通用性:
不仅支持二维矩阵乘法,还兼容一维向量内积和高维张量运算。 - 适用场景:
- 需要明确控制点积轴时(如自定义张量收缩)。
- 处理混合维度(如一维与二维数组相乘)。
- 替代方案:
- 若需纯矩阵乘法或广播行为,优先使用
@或np.matmul。
- 若需纯矩阵乘法或广播行为,优先使用
数组的索引与切片
多维数组的索引


数组的切片


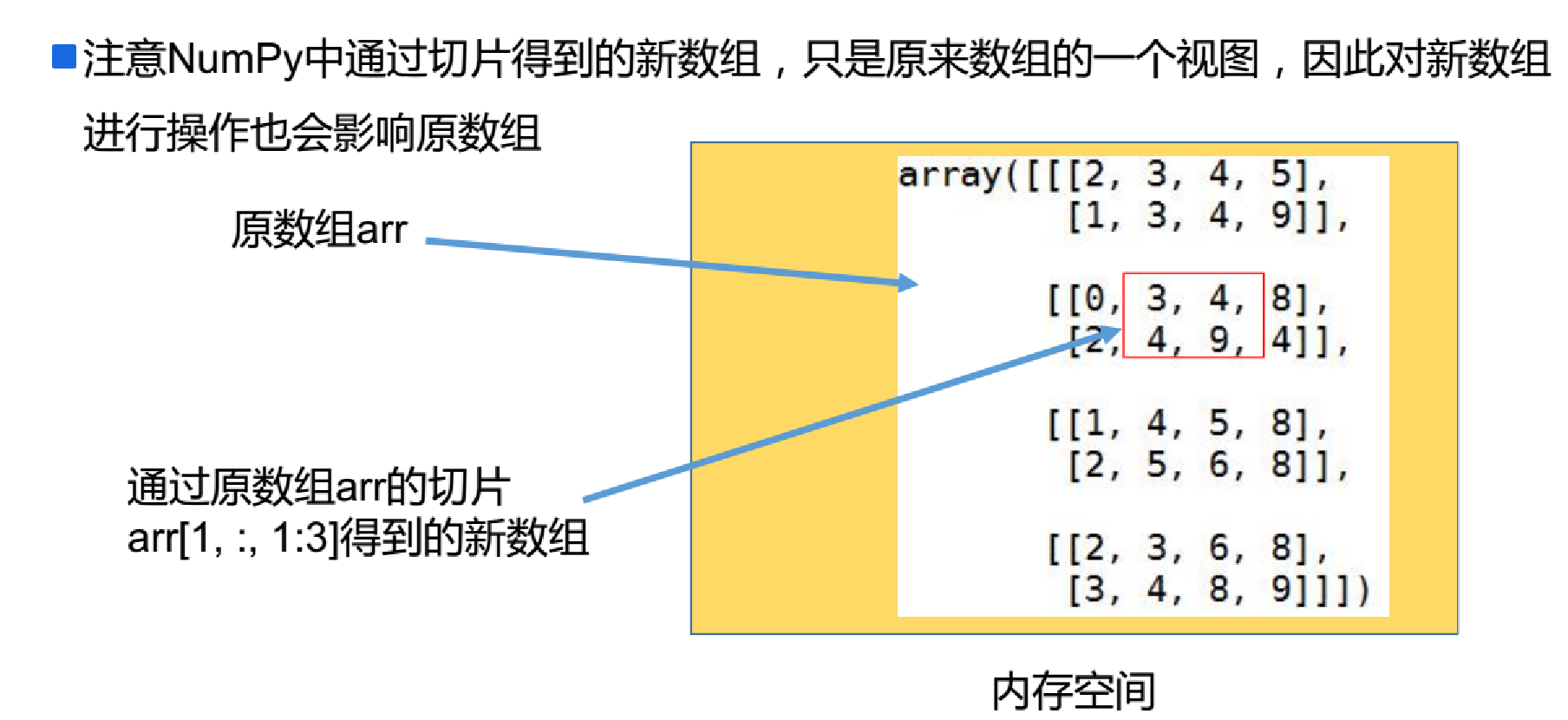
布尔类型索引

students=np.array(["张飞","关羽","刘备","曹操","孙权"])
scores=np.array([[ 70, 82, 101, 60, 72, 77],
[107, 96, 97, 61, 98, 60],
[ 69, 117, 97, 62, 76, 72],
[ 95, 86, 66, 66, 105, 111],
[111, 60, 81, 68, 70, 100]])
classs=np.array(["语文","数学","英语","物理","化学","生物"])
#获取刘备的成绩
liubei_score=scores[students=="刘备"]
print("刘备的成绩:\n",liubei_score)
print(liubei_score.reshape(-1))#去掉外面一层“[]”相当于降维[ 69 117 97 62 76 72]
#获取刘备的数学成绩
liubei_math_score=scores[students=="刘备"].reshape(-1)[classs=="数学"]
print("刘备的数学成绩:\n",liubei_math_score)
#获取刘备和曹操的成绩
liubei_caocao_score=scores[(students=="刘备")|(students=="曹操")]
print("刘备和曹操的成绩:\n",liubei_caocao_score)
#除了刘备和曹操之外的其他人的成绩
not_liubei_caocao_score=scores[(students!="刘备")&(students!="曹操")]
print("除了刘备和曹操之外的其他人的成绩:\n",not_liubei_caocao_score)输出结果:
刘备的成绩: [[ 69 117 97 62 76 72]] [ 69 117 97 62 76 72] 刘备的数学成绩: [117] 刘备和曹操的成绩: [[ 69 117 97 62 76 72] [ 95 86 66 66 105 111]] 除了刘备和曹操之外的其他人的成绩: [[ 70 82 101 60 72 77] [107 96 97 61 98 60] [111 60 81 68 70 100]]
花式索引
花式索引(Fancy indexing)指的是利用整数数组进行索引的方式
arr=np.arange(32).reshape(8,4) print(arr) print("-"*50) #!!!注意arr[3,2]是获取第四行的第三个数据等价于arr[3][2] print(arr[3,2]) print("-"*50) #获取第四行和第三行 print(arr[[3,2]])
[[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11] [12 13 14 15] [16 17 18 19] [20 21 22 23] [24 25 26 27] [28 29 30 31]] -------------------------------------------------- 14 -------------------------------------------------- [[12 13 14 15] [ 8 9 10 11]]
# 获取位置为(0,0)(4,3)(5,2)的数据 print(arr[[0,4,5],[0,3,2]]) print("-"*50) # 获取第1,5,6行第1,4,3列的数据 print(arr[[0,4,5]].T[[0,3,2]].T) print("-"*50) # 获取第1,5,6行第1,4,3列的数据:使用ix_函数产生的索引器 print(arr[np.ix_([0,4,5],[0,3,2])]) print("-"*50)
[ 0 19 22] -------------------------------------------------- [[ 0 3 2] [16 19 18] [20 23 22]] -------------------------------------------------- [[ 0 3 2] [16 19 18] [20 23 22]]
数组的转置与轴对换
数组转置是指将shape进行重置操作,并将其值重置为原始shape元组的倒置,比如原始的shape值为:(2,3,4),那么转置后的新元组的shape的值为: (4,3,2)f
对于二维数组而言(矩阵)数组的转置其实就是矩阵的转置;
可以通过调用数组的transpose函数或者T属性进行数组转置操作

| 特性 | .T 属性 |
transpose() 方法 |
|
|---|---|---|---|
| 功能范围 | 仅支持完全转置(反转所有轴)例如三维数组形状从 (a, b, c) 变为 (c, b, a) |
支持任意轴顺序的排列 | |
| 参数灵活性 | 无需参数 | 需指定 axes 参数(可选),通过 axes 参数自由指定轴的顺序 |
|
| 适用维度 | 适合二维数组快速转置 | 适合高维数组自定义轴顺序 | |
| 代码简洁性 | 更简洁(如 arr.T) |
稍复杂(如 arr.transpose(1,0,2)) |
|
| 示例 |
|
|
.T和transpose对比
内存与性能
视图而非副本:两者均返回原数组的视图(共享内存),修改转置后的数组会影响原数据。
性能一致:两者时间复杂度相同(O(1)),无显著性能差异。
transpose(axes)应用场景
- 调整高维数据轴顺序(如深度学习中的张量格式转换):
# 将图像数据从 (batch, height, width, channels) 转换为 (batch, channels, height, width)在深度学习和批量数据处理中,图像数据的维度通常会被扩展为四维数组 images = np.random.rand(32, 224, 224, 3) reshaped = images.transpose(0, 3, 1, 2) # 形状 (32, 3, 224, 224) #了解内容: 当处理批量图像数据时,四维数组的维度含义为: (batch_size, height, width, channels) batch_size:一次性处理的图像数量(如32张图)。 height/width:单张图像的分辨率(如224x224)。 channels:颜色通道数(如RGB图像的3通道)。
通用函数
ufunc:numpy模块中对ndarray中数据进行快速元素级运算的函数,也可以看做是简单的函数(接受一个或多个标量值,并产生一个或多个标量值)的矢量化包装器。
主要包括一元函数和二元函数;
一元函数
|
一元ufunc |
描述 |
调用方式 |
|
abs, fabs |
计算整数、浮点数或者复数的绝对值,对于非复数,可以使用更快的fabs |
np.abs(arr) |
|
sqrt |
计算各个元素的平方根,相当于arr ** 0.5, 要求arr的每个元素必须是非负数 |
np.sqrt(arr) |
|
square |
计算各个元素的平方,相当于arr ** 2 |
np.square(arr) |
|
exp |
计算各个元素的指数e的x次方 |
np.exp(arr) |
|
log、log10、log2、log1p |
分别计算自然对数、底数为10的log、底数为2的log以及log(1+x); 要求arr中的每个元素必须为正数 |
np.log(arr) |
|
sign |
计算各个元素的正负号: 1 正数,0:零,-1:负数 |
np.sign(arr) |
|
ceil |
计算各个元素的ceiling值,即大于等于该值的最小整数 |
np.ceil(arr) |
|
floor |
计算各个元素的floor值,即小于等于该值的最大整数 |
np.floor(arr) |
|
rint |
将各个元素值四舍五入到最接近的整数,保留dtype的类型 |
np.rint(arr) |
|
modf |
将数组中元素的小数位和整数位以两部分独立数组的形式返回 |
np.modf(arr) |
|
isnan |
返回一个表示“那些值是NaN(不是一个数字)”的布尔类型数组 |
np.isnan(arr) |
|
isfinite、isinf |
分别一个表示”那些元素是有穷的(非inf、非NaN)”或者“那些元素是无穷的”的布尔型数组 |
np.isfinite(arr) |
|
cos、cosh、sin、sinh、tan、tanh |
普通以及双曲型三角函数 |
np.cos(arr) |
|
arccos、arccosh、arcsin、arcsinh、arctan、arctanh |
反三角函数 |
np.arccos(arr) |
arr=np.array([-2.2,-5.5,-5,0,2,3,8,7,6]) print("arr=",arr) newarr=np.fabs(arr)+1 print("np.abs(arr)=",np.abs(arr)) print("np.fabs(arr)=",np.fabs(arr)) print("np.sqrt(arr)=",np.sqrt(newarr)) print("np.square(arr)=",np.square(arr)) print("np.exp(arr)=",np.exp(arr)) print("np.log(newarr)=",np.log(newarr)) print("np.log10(newarr)=",np.log10(newarr)) print("np.sign(arr)=",np.sign(arr)) print("np.ceil(arr)=",np.ceil(arr)) print("np.floor(arr)=",np.floor(arr)) print("np.rint(arr)=",np.rint(arr)) print("np.modf(arr)=",np.modf(arr)) print("np.isnan(arr)=",np.isnan(arr)) print("np.isfinite(arr)=",np.isfinite(arr)) print("np.cos(arr)=",np.cos(arr)) print("np.arccos(newarr)=",np.arccos(np.cos(arr)))
arr= [-2.2 -5.5 -5. 0. 2. 3. 8. 7. 6. ] np.abs(arr)= [2.2 5.5 5. 0. 2. 3. 8. 7. 6. ] np.fabs(arr)= [2.2 5.5 5. 0. 2. 3. 8. 7. 6. ] np.sqrt(arr)= [1.78885438 2.54950976 2.44948974 1. 1.73205081 2. 3. 2.82842712 2.64575131] np.square(arr)= [ 4.84 30.25 25. 0. 4. 9. 64. 49. 36. ] np.exp(arr)= [1.10803158e-01 4.08677144e-03 6.73794700e-03 1.00000000e+00 7.38905610e+00 2.00855369e+01 2.98095799e+03 1.09663316e+03 4.03428793e+02] np.log(newarr)= [1.16315081 1.87180218 1.79175947 0. 1.09861229 1.38629436 2.19722458 2.07944154 1.94591015] np.log10(newarr)= [0.50514998 0.81291336 0.77815125 0. 0.47712125 0.60205999 0.95424251 0.90308999 0.84509804] np.sign(arr)= [-1. -1. -1. 0. 1. 1. 1. 1. 1.] np.ceil(arr)= [-2. -5. -5. 0. 2. 3. 8. 7. 6.] np.floor(arr)= [-3. -6. -5. 0. 2. 3. 8. 7. 6.] np.rint(arr)= [-2. -6. -5. 0. 2. 3. 8. 7. 6.] np.modf(arr)= (array([-0.2, -0.5, -0. , 0. , 0. , 0. , 0. , 0. , 0. ]), array([-2., -5., -5., 0., 2., 3., 8., 7., 6.])) np.isnan(arr)= [False False False False False False False False False] np.isfinite(arr)= [ True True True True True True True True True] np.cos(arr)= [-0.58850112 0.70866977 0.28366219 1. -0.41614684 -0.9899925 -0.14550003 0.75390225 0.96017029] np.arccos(newarr)= [2.2 0.78318531 1.28318531 0. 2. 3. 1.71681469 0.71681469 0.28318531]
二元函数
|
二元ufunc |
描述 |
调用方式 |
|
mod |
元素级的取模(就是arr1对arr2取余) |
np.mod(arr1,arr2) |
|
dot |
求两个数组的点积(所有对应的点的乘积之和) |
np.dot(arr1,arr2) |
|
greater、greater_equal、less、less_equal、equal、not_equal |
执行元素级别的比较运算,最终返回一个布尔型数组 greater:(arr1>arr2)、greater_equal:(arr1>=arr2)、less:(arr1<arr2)、less_equal:(arr1<=arr2)、equal:(arr1==arr2)、not_equal |
np.greater(arr1, arr2) np.less(arr1, arr2) np.equal(arr1, arr2) |
|
logical_and、 logical_or、 logical_xor |
执行元素级别的布尔逻辑运算,相当于中缀运算符&、|、^(与或非) 如: A = np.array([True, False, True, False]) |
np.logical_and(arr1,arr2) np.logical_or(arr1,arr2) np.logical_xor(arr1,arr2) |
|
power |
求解对数组中的每个元素进行给定次数的指数值,类似于: arr ** 3 |
np.power(arr, 3) |

聚合函数:统计运算
聚合函数是对一组值(eg一个数组)进行操作,返回一个单一值作为结果的函数。当然聚合函数也可以指定对某个具体的轴进行数据聚合操作;
常将的聚合操作有:平均值、最大值、最小值、标准差等等。
- min(a,axis)
- 返回数组的最小值或轴向的最小值。
- max(a, axis])
- 返回数组的最大值或轴向的最大值。
- median(a, axis)
- 计算指定轴上的中位数。
- mean(a,axis, dtype)
- 沿指定轴计算算术平均值。
- ·std(a,axis, dtype)
- 计算沿指定轴线的标准差。
- ·var(a,axis,dtype)
- 计算指定轴上的方差。
arr=np.array([[1,2,3,4],[5,6,7,8]]) arr print("最小值",np.min(arr)) print("最小值",arr.min()) print("最大值",np.max(arr)) print("中位数",np.median(arr)) print("平均值",np.mean(arr)) print("方差",np.var(arr)) print("标准差",np.std(arr)) print("自己计算的标准差",np.sqrt(np.power(arr-np.mean(arr),2).sum()/arr.size))
最小值 1 最小值 1 最大值 8 中位数 4.5 平均值 4.5 方差 5.25 标准差 2.29128784747792 自己计算的标准差 2.29128784747792
arr=np.array([[1,2,3,4],[5,6,7,8]]) print(arr) # 二维数组情况下axis=0表示对同列数据进行聚合 print("同列最小值:",arr.min(axis=0)) print("同列平均值",arr.mean(axis=0)) print("同列之和",arr.sum(axis=0)) # axis=1表示对同行数据进行聚合 print("同行最小值",arr.min(axis=1)) print("同行平均值",arr.mean(axis=1)) print("同行之和",arr.sum(axis=1))
[[1 2 3 4] [5 6 7 8]] 同列最小值: [1 2 3 4] 同列平均值 [3. 4. 5. 6.] 同列之和 [ 6 8 10 12] 同行最小值 [1 5] 同行平均值 [2.5 6.5] 同行之和 [10 26]

# 接下来对于前四名学生,进行一些统计运算 temp = scores[:4] # 按照列统计 print("前四名学生,各科成绩的最大分:{}".format(np.max(temp, axis=0))) print("前四名学生,各科成绩的最小分:{}".format(np.min(temp, axis=0))) print("前四名学生,各科成绩波动情况:{}".format(np.std(temp, axis=0))) print("前四名学生,各科成绩的平均分:{}".format(np.mean(temp, axis=0)))
前四名学生,各科成绩的最大分:[98 85 93 89 96 71] 前四名学生,各科成绩的最小分:[51 69 44 53 61 62] 前四名学生,各科成绩波动情况:[18.26198237 5.67340286 17.86756839 13.49768499 12.77693234 3.5 ] 前四名学生,各科成绩的平均分:[78. 77.25 64.5 74.75 75.5 67.5 ]
# 接下来对于前四名学生,进行一些统计运算 temp = scores[:4] # 安照行统计 print("前四名学生,各自最高成绩:{}".format(np.max(temp, axis=1))) print("前四名学生,各自最低成绩:{}".format(np.min(temp, axis=1))) print("前四名学生,偏科情况:{}".format(np.std(temp, axis=1))) print("前四名学生,各个学生的平均分:{}".format(np.mean(temp, axis=1)))
前四名学生,各自最高成绩:[74 98 96 82] 前四名学生,各自最低成绩:[51 61 44 58] 前四名学生,偏科情况:[ 8.1240384 12.80299444 17.74589154 7.36357401] 前四名学生,各个学生的平均分:[62. 80.5 77.5 71.66666667]

前四名学生,各科成绩最高分对应的学生下标:[1 1 1 2 2 1]条件判断
np.all()

np.any()

np.where()(三元运算符)
np.where函数是三元表达式x if condition else y的矢量化版本。
就是从两个数组里选出符合条件的元素,重新组成新数组并返回。(建议直接看例子)




x=np.array([-1,-999,-1.2,-3.3]) y=np.array([-2,-2.1,-2.2,-2.3]) condition=x<y#false
#传统写法 res1=[x if c else y for (x,y,c) in zip(x,y,condition)]
#where语句 res2=np.where(condition,x,y) print("使用python语法计算结果为:",res1,"数据类型为:",type(res1)) print("使用where语法计算结果为:",res2,"数据类型为:",type(res2))
使用python语法计算结果为: [-2.0, -999.0, -2.2, -3.3] 数据类型为: <class 'list'> 使用where语法计算结果为: [ -2. -999. -2.2 -3.3] 数据类型为: <class 'numpy.ndarray'>
案例:将数组中的所有异常数字替换为0,比如将NaN替换为0
arr=np.array([[1,2,np.NaN,4],[3,5,6,7],[8,9,np.inf,np.NaN],[8,np.inf,np.inf,10]])
print(arr)
zeros=np.zeros(arr.shape)
print(zeros)
condition=(np.isinf(arr))|(np.isnan(arr))|(arr=='')
print(condition)
res1=np.where(condition,zeros,arr)
res2=np.where(condition,0,arr)
print(res1)
print(res2)[[ 1. 2. nan 4.] [ 3. 5. 6. 7.] [ 8. 9. inf nan] [ 8. inf inf 10.]] [[0. 0. 0. 0.] [0. 0. 0. 0.] [0. 0. 0. 0.] [0. 0. 0. 0.]] [[False False True False] [False False False False] [False False True True] [False True True False]] [[ 1. 2. 0. 4.] [ 3. 5. 6. 7.] [ 8. 9. 0. 0.] [ 8. 0. 0. 10.]] [[ 1. 2. 0. 4.] [ 3. 5. 6. 7.] [ 8. 9. 0. 0.] [ 8. 0. 0. 10.]]
where复合逻辑需要结合np.logical_and和np.logical_or使用:
np.logical_and和np.logical_or
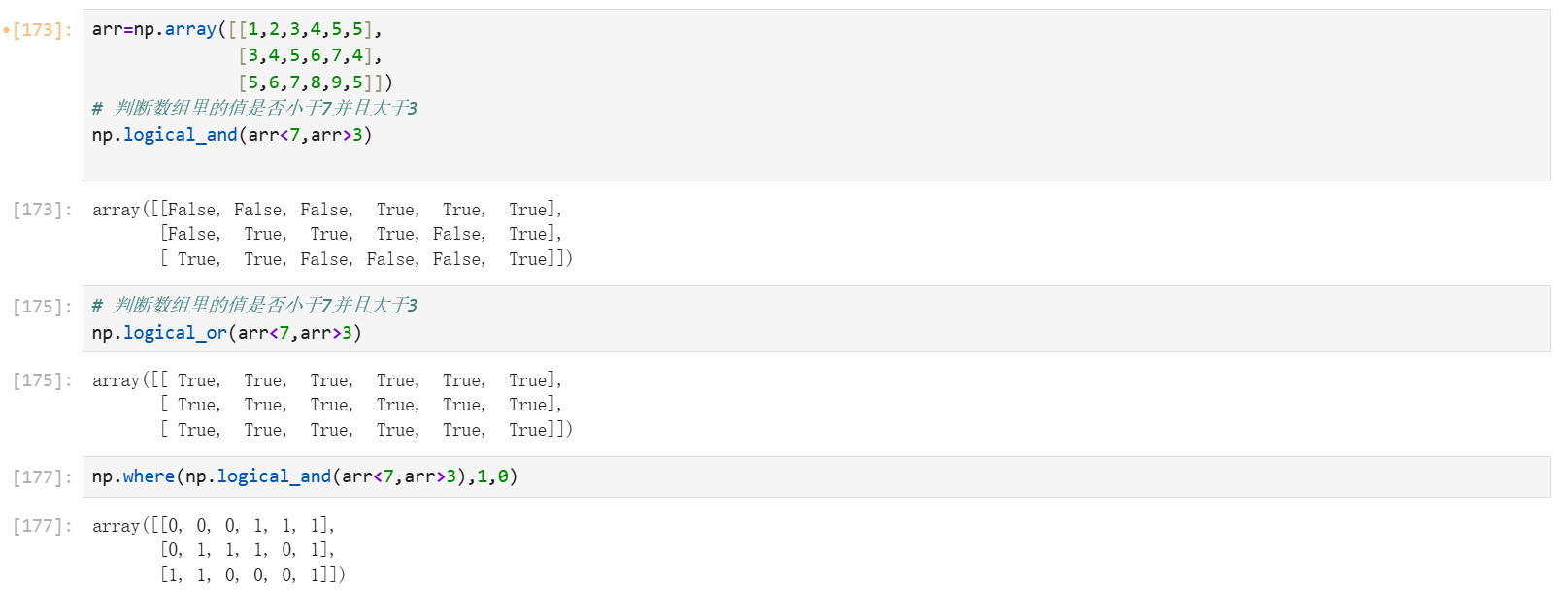
np.unique:数组去重
np.unique 用于查找数组中的唯一元素(去重),并返回排序后的结果。支持以下扩展功能:
- 返回唯一元素的首次出现索引。
- 返回从唯一数组重建原数组的逆索引。
- 统计每个唯一元素的出现次数。
- 支持处理多维数组(沿指定轴操作)。
参数详解
| 参数 | 类型 | 说明 |
|---|---|---|
ar |
array_like | 输入数组。默认会展开为一维数组(除非指定 axis)。 |
return_index |
bool | 若为 True,返回原数组中唯一元素的首次出现索引。默认 False。 |
return_inverse |
bool | 若为 True,返回逆索引数组,用于从唯一数组重建原数组。默认 False。 |
return_counts |
bool | 若为 True,返回每个唯一元素的出现次数。默认 False。 |
axis |
int/None | 指定操作的轴。默认 None(展开为一维数组)。支持多维数组处理。 |
equal_nan |
bool | 若为 True,将多个 NaN 视为相同值。默认 True(自 NumPy 1.24 起)。 |
返回值
| 返回值 | 说明 |
|---|---|
unique |
排序后的唯一元素数组。 |
unique_indices |
(可选)原数组中唯一元素的首次出现索引。需 return_index=True。 |
unique_inverse |
(可选)逆索引数组,用于重建原数组。需 return_inverse=True。 |
unique_counts |
(可选)每个唯一元素出现的次数。需 return_counts=True。 |
示例解析
(1) 基本用法:一维数组去重
import numpy as np arr = np.array([1, 1, 2, 2, 3, 3]) unique_values = np.unique(arr) print(unique_values) # 输出: [1 2 3]
二维、多维数组去重

二维数组按行去重
arr_2d = np.array([[1, 0, 0], [1, 0, 0], [2, 3, 4]]) unique_rows = np.unique(arr_2d, axis=0) print(unique_rows) # 输出: # [[1 0 0] # [2 3 4]]
二维数组按列去重
arr = np.array([[1, 2, 1], [1, 4, 1], [1, 2, 1]]) unique_subarrays = np.unique(arr, axis=1) # 按列去重 unique_subarrays #输出 array([[1, 2], [1, 4], [1, 2]])

应用场景
- 数据清洗:去除重复值或处理缺失值(如合并多个
NaN)。 - 统计分析:计算唯一值的频率分布。
- 机器学习:预处理分类标签或特征编码。
np.round:四舍五入,指定保留小数位数
numpy.round 用于对数组中的数值进行四舍五入,支持以下操作:
- 指定保留的小数位数(
decimals参数)。 - 处理正/负小数位数(如
decimals=-1表示舍入到十位)。 - 支持复数(实部和虚部分别四舍五入)。
- 提供中间值舍入规则(向最近的偶数值舍入)。
参数说明
| 参数 | 类型 | 说明 |
|---|---|---|
a |
array_like | 输入数组(支持整数、浮点数、复数)。 |
decimals |
int | 保留的小数位数。默认 0(舍入到整数);负数表示舍入到十、百、千位等。 |
out |
ndarray | 可选输出数组,用于直接存储结果(需与原数组形状相同)。 |
基本舍入
arr = np.array([0.37, 1.64]) print(np.round(arr)) # 输出: [0., 2.] print(np.round(arr, decimals=1)) # 输出: [0.4 1.6]
负数小数位数
arr = np.array([1, 2, 3, 11]) print(np.round(arr, decimals=-1)) # 输出: [0, 0, 0, 10](舍入到十位)
原地修改数组
arr = np.array([1.234, 5.678]) out = np.empty_like(arr) np.round(arr, decimals=1, out=out) # 结果存入 out print(out) # 输出: [1.2 5.7]
关键行为特性
中间值舍入规则
当数值恰好在两个可能的舍入结果中间时,numpy.round 会舍入到最接近的偶数值:采用 “四舍六入五成双”(Round Half to Even),当末尾是 5 时向最近的偶数方向舍入。
import numpy as np print(np.round([0.5, 1.5, 2.5, 3.5])) # 输出: [0., 2., 2., 4.]
浮点数精度问题
由于 IEEE 754 浮点数标准的限制,某些十进制小数无法精确表示为二进制浮点数,导致舍入结果可能与预期不符:
# 示例:16.055 的二进制表示存在误差 print(np.round(16.055, 2)) # 输出: 16.06(因实际存储值接近 16.0549999999999997) print(round(16.055, 2)) # 输出: 16.05(Python 内置 round 更精确)
高精度数值的舍入误差
对于极大或极小的数值,numpy.round 的快速算法可能导致额外误差:
# 大数值舍入示例 print(np.round(56294995342131.5, 3)) # 输出: 56294995342131.51(误差) print(np.format_float_positional(56294995342131.5, precision=3)) # 输出: '56294995342131.5'
性能与精度权衡
| 方法 | 速度 | 精度 | 适用场景 |
|---|---|---|---|
numpy.round |
快 | 一般 | 大规模数值处理 |
Python 内置 round |
慢 | 高 | 单个浮点数精确舍入 |
np.format_float_* |
慢 | 高 | 显示格式化(不修改数据) |
总结
- 中间值舍入规则:向最近的偶数值舍入,避免统计偏差。
- 浮点数精度陷阱:理解二进制存储限制,必要时使用高精度工具。
- 替代方案选择:根据需求在速度与精度间权衡。
通过合理使用 numpy.round 及其替代方法,可有效平衡数值处理的效率与准确性。
np.rint(x)和np.round(x, decimals=0)
| 对比维度 | np.rint(x) | np.round(x, decimals=0) |
|---|---|---|
| 小数位数控制 | 不支持,只能四舍五入到整数 | 支持通过 decimals 参数指定任意小数位数 |
| 主要用途 | 专门用于取最接近的整数 | 灵活处理不同精度的四舍五入需求 |
| 对 0.5 的处理 | 四舍五入到最近的偶数(银行家舍入) | 与 rint 相同(银行家舍入规则) |
| 返回类型 | 始终为浮点数数组 | 始终为浮点数数组 |
补充
科学计数法
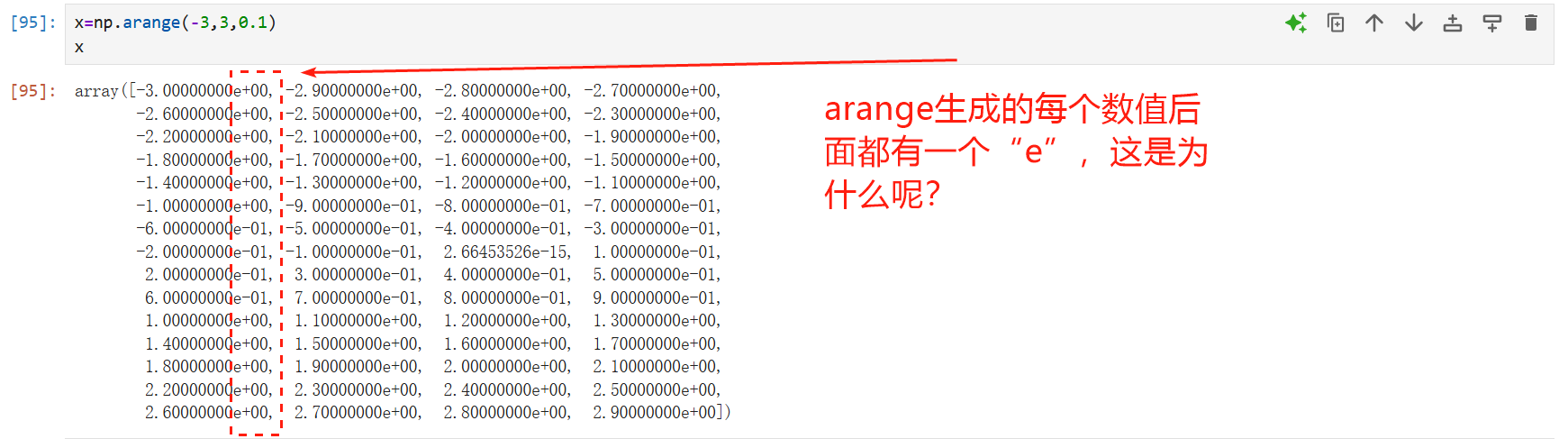
在 NumPy 中,np.arange(-3, 3, 0.1) 生成的数组元素末尾的 e 表示科学计数法(例如 1.5e-16 即 1.5×10⁻¹⁶)。这是因为浮点数精度问题导致某些数值无法精确表示,而 NumPy 默认使用科学计数法显示极小或极小的数值。以下是详细解释和解决方案:
为什么会出现 e(科学计数法)?
- 浮点数精度限制
计算机用二进制存储小数时,某些十进制数(如0.1)无法精确表示,导致微小误差。例如:
0.1 的实际存储值 ≈ 0.10000000000000000555...
NumPy 的默认显示规则
当数值绝对值小于 1e-4 或大于 1e+16 时,NumPy 会自动使用科学计数法。例如:
x = np.array([0.0001, 10000000000000000.0]) print(x) # 输出: [1.e-04 1.e+16]
为什么你的 np.arange(-3, 3, 0.1) 会出现科学计数法?
-
误差积累导致极小值
由于0.1的浮点误差,某些数值的实际计算结果可能接近0(例如-3.0 + 0.1 * 30 = 0.0,但实际值可能是-1.11e-16),触发科学计数法显示。 -
验证示例
检查数组中是否包含极小值:
import numpy as np x = np.arange(-3, 3, 0.1) print(x[x < 1e-10]) # 输出接近 0 的极小值,如 [-1.11e-16]
如何强制禁用科学计数法?
通过 np.set_printoptions 调整显示规则:
方法一:禁用科学计数法(推荐)
import numpy as np # 禁用科学计数法,并设置小数点后显示位数(例如4位) np.set_printoptions(suppress=True, precision=4) x = np.arange(-3, 3, 0.1) print(x)
输出示例:
[-3. -2.9 -2.8 ... 2.8 2.9]方法二:自定义格式(高级)
# 强制所有浮点数用小数点显示,保留5位小数 np.set_printoptions(formatter={'float': '{:0.5f}'.format}) x = np.arange(-3, 3, 0.1) print(x)
输出示例:
[-3.00000 -2.90000 -2.80000 ... 2.80000 2.90000]数值本质未改变
科学计数法只是显示方式,不影响实际数值的精度。例如:
a = 1e-16 b = 0.0000000000000001 print(a == b) # True
总结
| 现象 | 原因 | 解决方案 |
|---|---|---|
数值末尾有 e |
浮点精度误差触发科学计数法 | 使用 np.set_printoptions 禁用 |
| 显示异常但计算正确 | 显示规则不同,数值未改变 | 无需处理,关注实际计算逻辑 |
调整打印选项后,所有数值将以常规小数形式显示。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号