数学基础概念

因为今天的各种人工智能技术都是建立在数学模型基础之上的，必备的数学统计学知识是理解人工智能的基础，所以作为 AI 产品经理来说，这些基础知识也是必须要学习的。

虽然不需要了解数学公式，以及公式背后的逻辑，但我们需要知道数学统计学的基本概念，以及概念的落地应用。

 

数的分类

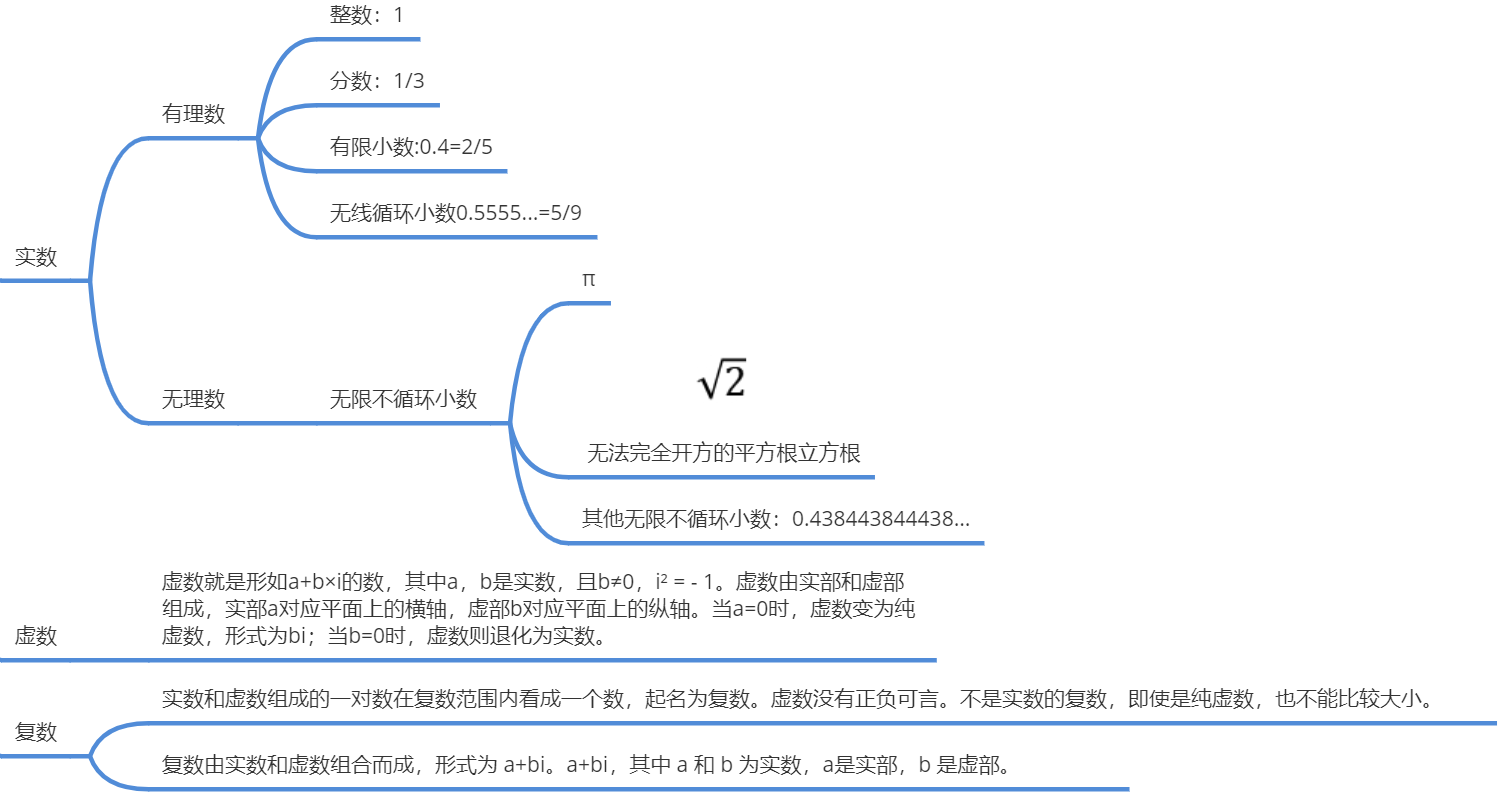
常数（Constant）​​：在运算过程中​​值不发生变化​​的量。

• ​​示例​​：
  • 数值常数：$5$、$\pi$、$e$（自然对数的底）。
  • 符号常数：在方程 $y=kx+b$ 中，$k$ 和 $b$ 可以是常数（如 $k=2$, $b=3$）。

统计学

概率统计中的常见分布

在概率统计中，我们最需要掌握的就是概率的分布。举个例子，我们在做一个预测用户评分的时候，这个分数可能是购买倾向，也可能是信用评分。按照经验，这个评分结果应该是符合正态分布的。这个时候，如果算法同学的模型预测出来的结果不符合正态分布，我们就必须对这个结果进行质疑，让他们给出合理的解释。

从这个例子中我们知道，概率分布是我们用来评估特征数据和模型结果的武器。 那产品经理怎么才能利用好这个武器呢？首先，我们要掌握常用的概率分布的类型。其次，我们还要知道业务场景下的特征数据和模型结果的分布，以及它们应该符合哪种分布类型。这样，产品经理就可以把概率分布应用于日常的工作中。因为概率的分布和随机变量的类型相关，随机变量又可以分为离散型随机变量和连续性随机变量两种。为了方便你查看，我把这两种变量对应的概率分布的类型都总结在了下面这张图里。

伯努利分布

伯努利分布（Bernoulli Distribution）是一种离散概率分布，专门用于描述仅有两种可能结果的随机事件。

1. 定义：伯努利分布指的是对于随机变量X，参数为p（0≤p≤1），如果它分别以概率p和1-p取1和0为值。其中，1代表成功，0代表失败。

2. 特点：

   • 离散型分布：伯努利分布是离散型概率分布，随机变量只能取0或1这两个值。
   • 单参数分布：伯努利分布只有一个参数p，即成功的概率。
   • 基础分布：伯努利分布是二项分布、几何分布、负二项分布等更复杂分布的基础。

应用场景

伯努利分布在现实生活中具有广泛的应用，包括但不限于以下几个方面：

1. 医学领域：可以用来描述某种疾病在特定人群中的发生率。
2. 计算机科学：可以用来模拟计算机在运行过程中是否出现故障。
3. 市场营销：可以用来预测客户是否会购买某种产品。
4. 二分类问题：常用于信用评分、疾病诊断等二分类问题的建模和分析。

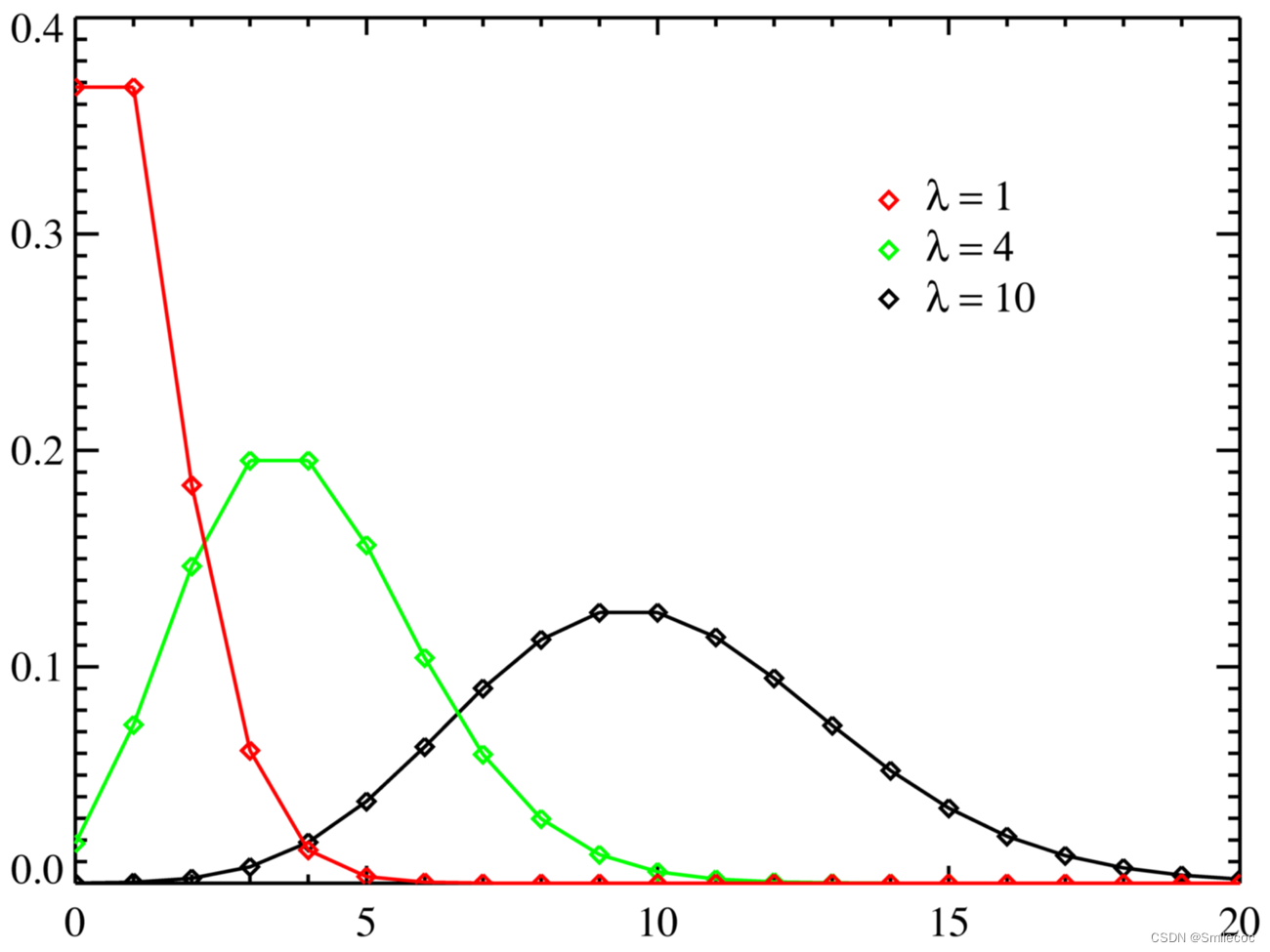
泊松分布

泊松分布描述的是单位时间内，随机事件发生的次数。 比如，我们的频道页平均每分钟就有 2000 次访问，那如果让我们计算出下一分钟能够有 4000 次访问的概率，这个结果就是泊松分布。

二项分布近似于泊松分布(泊松定理)在实验次数n 比较多的情况下，二项分布的概率计算比较麻烦,这时就可以用泊松分布来近似处理二项分布.

 

正态分布

正态分布是一种概率分布。正态分布是具有两个参数μ和σ的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ是此随机变量的标准差，所以正态分布记作N(μ，σ )。

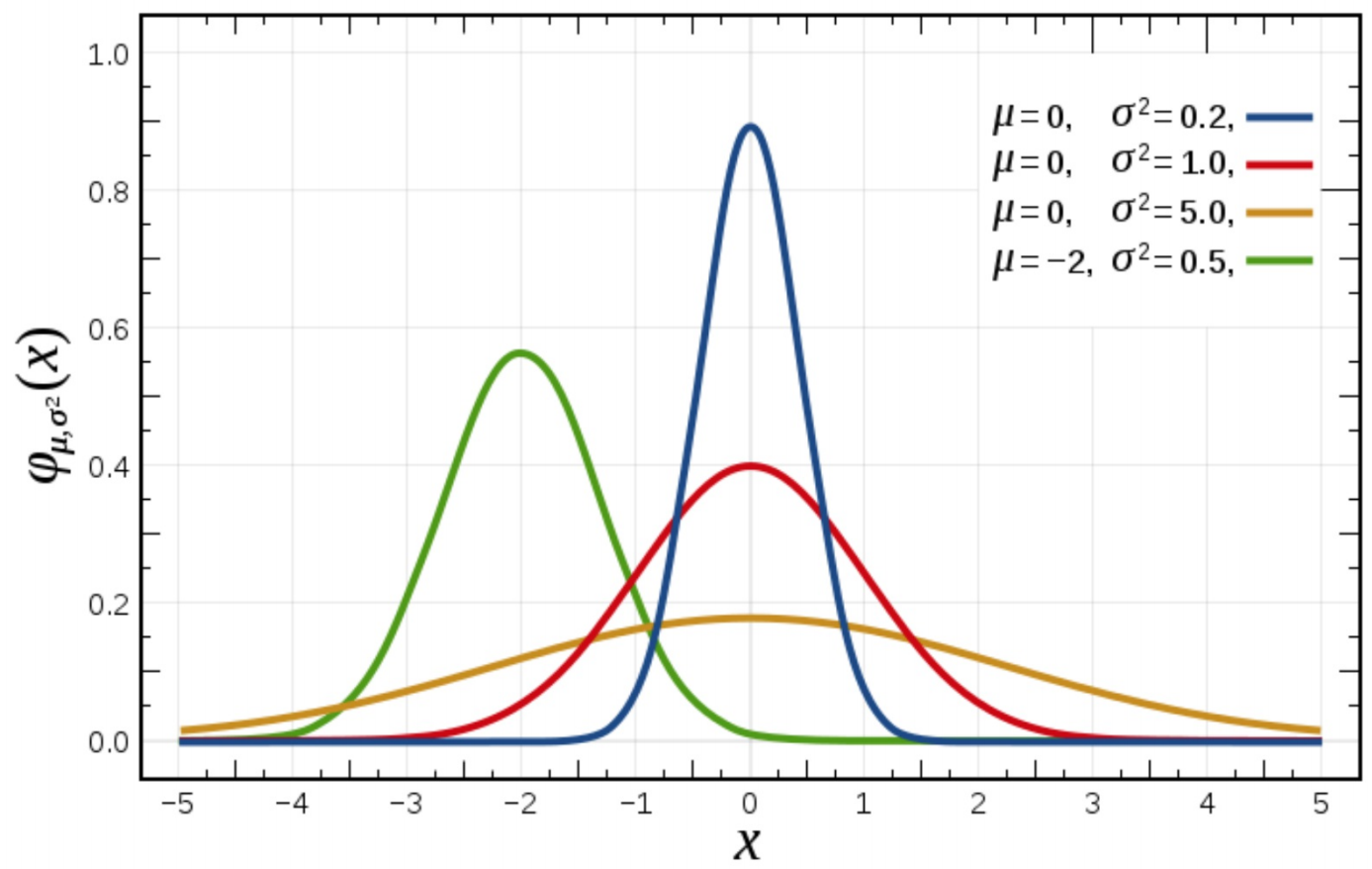
它也叫高斯分布。正态分布的曲线特点是两头低、中间高，左右对称，所以我们也经常叫它钟形曲线。

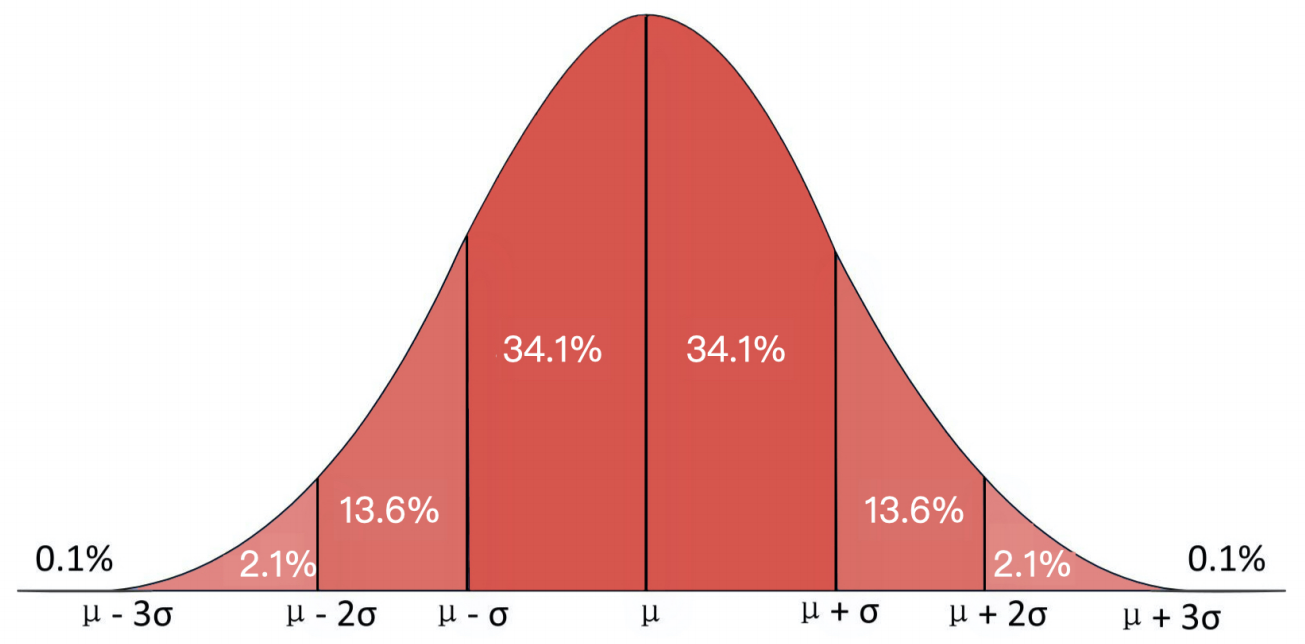
正态分布的应用

在现实生活中，人的很多特质都符合正态分布，比如人的身高、体重、运动量、智力、收入、甚至信用情况等等。

正态分布特点

μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

标准差如何来？

• 方差

是在概率论和统计方差衡量一组数据时离散程度的度量

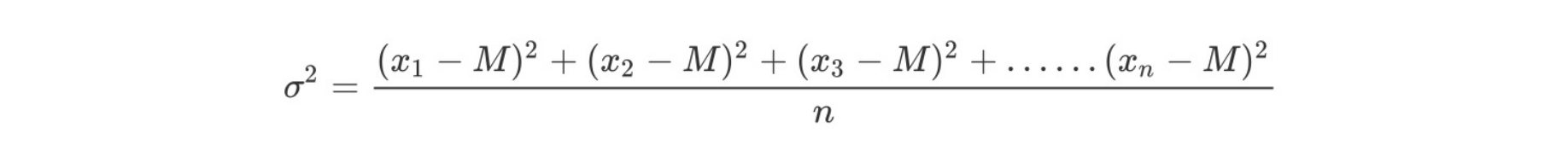
其中M为平均值，n为数据总个数，σ 为标准差，σ ^2可以理解一个整体的方差

标准差与方差的意义

可以理解成数据的一个离散程度的衡量

几何

斜率

斜率表示一条平面上直线关于坐标轴的倾斜程度，符号为字母k。它通常用直线与坐标轴夹角（倾斜角）的正切来定义，也等于直线上两点的纵坐标之差与横坐标之差的比来表示。需要注意的是，当直线与纵坐标轴平行时，斜率不存在。

利用斜率可以解决一些数学问题，可以用来表示直线方程，还可以为一些代数式提供几何直观，如一次函数的表达式为y=kx+b，其图象为一条直线，表达式中的k即为该直线的斜率。