02.深度学习（Deep Learning）概述

深度学习（Deep Learning）是一种特殊的机器学习，（也称为深度结构学习【Deep Structured Learning】、层次学习【Hierarchical Learning】或者是深度机器学习【Deep Machine Learning】）是一类算法集合，是机器学习的一个分支。是借鉴了人脑由很多神经元组成的特性而形成的一个框架。相对于普通的机器学习，深度学习在海量数据情况下的效果要比机器学习更为出色。

我们从上面的“人工智能技术发展时间线”图中也可以分析出来，深度学习是在互联网 DT时代（数据处理技术时代，Data Technology）到来之后才逐渐火起来的，所以数据量对深度学习的重要性是非常高的。

深度学习方法近年来，在会话识别、图像识别和对象侦测等领域表现出了惊人的准确性。

但是，“深度学习”这个词语很古老，它在1986年由Dechter在机器学习领域提出，然后在2000年有Aizenberg等人引入到人工神经网络中。而现在，由于Alex Krizhevsky在2012年使用卷积网络结构赢得了ImageNet比赛之后受到大家的瞩目。

并且，自从 2016 年 Alpha Go 打败了李世石之后，深度学习就正式确立了在机器学习领域中的霸主地位。可以说，目前所有应用了人工智能的行业，基本都用到了深度学习模型。

如何理解深度学习？

因为深度学习可以简单理解为多层的神经网络模型，所以想要理解深度学习，我们就要先理解神经网络。接下来，我就通过一个例子来讲讲什么是神经网络。

什么是神经网络？

假如，你就职于一家很“民主”的公司，每年年终总结的时候，公司会让每名员工写下自己对公司的意见，并且收集起来。为了节约行政成本，这些意见都会由当前层级的领导整合后，提交给他的上一级领导。

比如说，每个“部门组长”收集所有“部门员工”的意见，整合后统一提交给所有“部门经理”。每个“部门经理”收集所有“部门组长”的意见，整合后统一提交给所有“事业群经理”。就这样层层汇总传递，最后由事业群经理汇总提交给总经理：

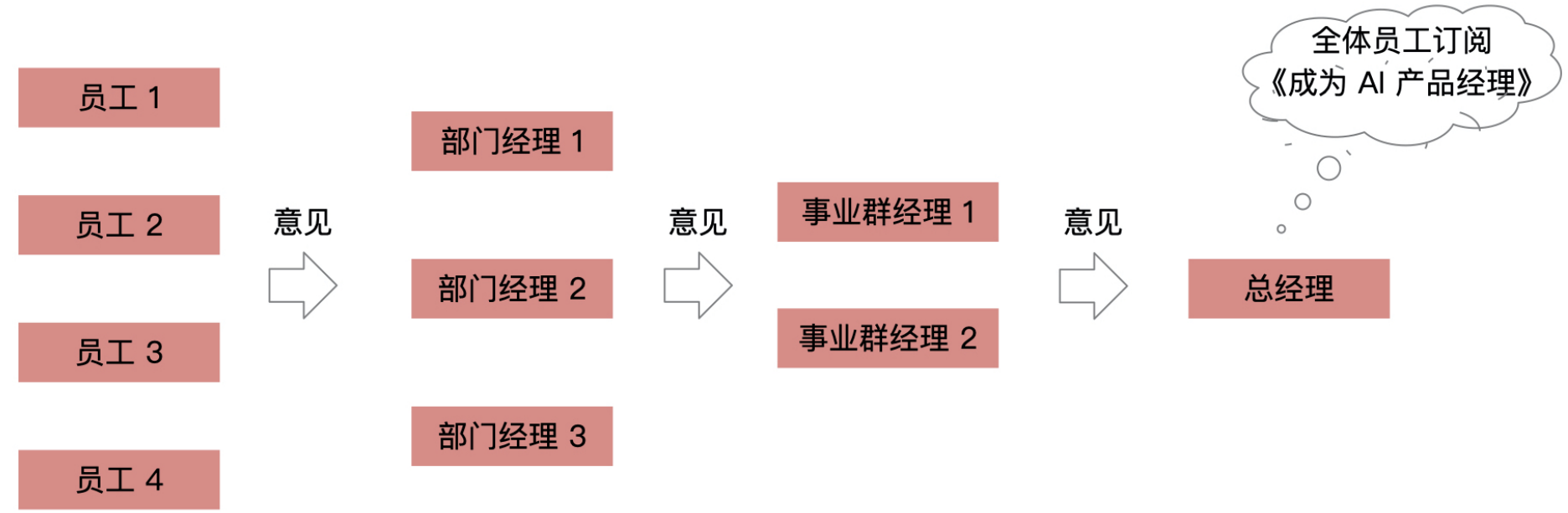
这个例子其实完全可以通过机器学习模型来描述：

把每个“员工”的意见，想象成机器学习中的“特征”，

把每一层“领导”对收集上来的意见的整合，想象成当前层级的“输出”，

最后把“总经理”收到的结果想象成模型的“最终输出”。

这样一来，就形成了一个多层级的机器学习模型，也就是我们说的神经网络。

具体来说，我们可以把这个神经网络用三层结构来表示，分别为输入层、隐藏层，以及输出层。其中，隐藏层对我们来说是黑盒，隐藏层中的每上一个隐藏层的输出都是下一个隐藏层的输入，每一层都是在表达一种中间特征，目的是将特征做非线性高阶变换。

在这个神经网络的结构中，不同层级之间的联系是非常紧密的，因为每个连接层之间的节点（领导），都会和上下两个层级中的所有节点（领导）进行沟通。我们也把这种结构叫做全连接神经网络模型。

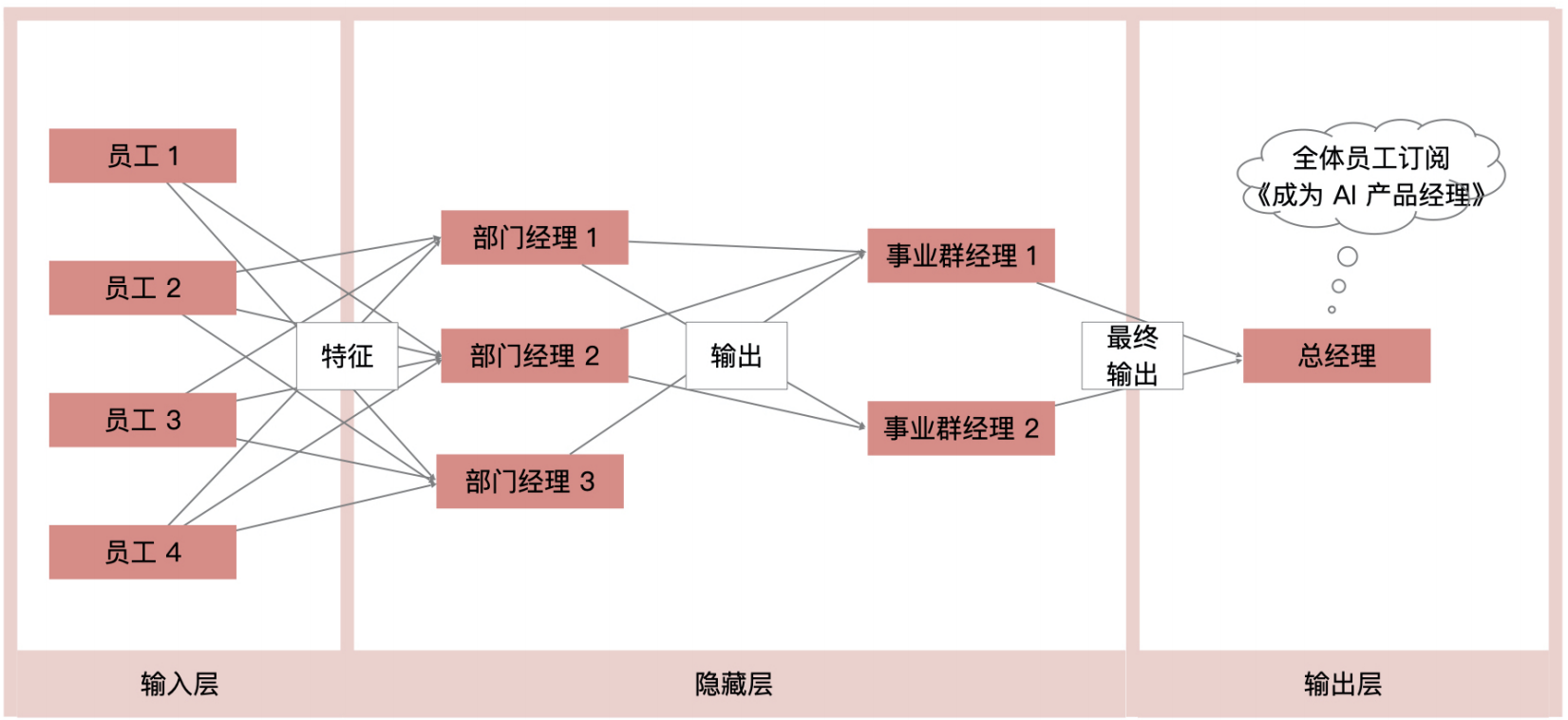
神经网络模型的组成

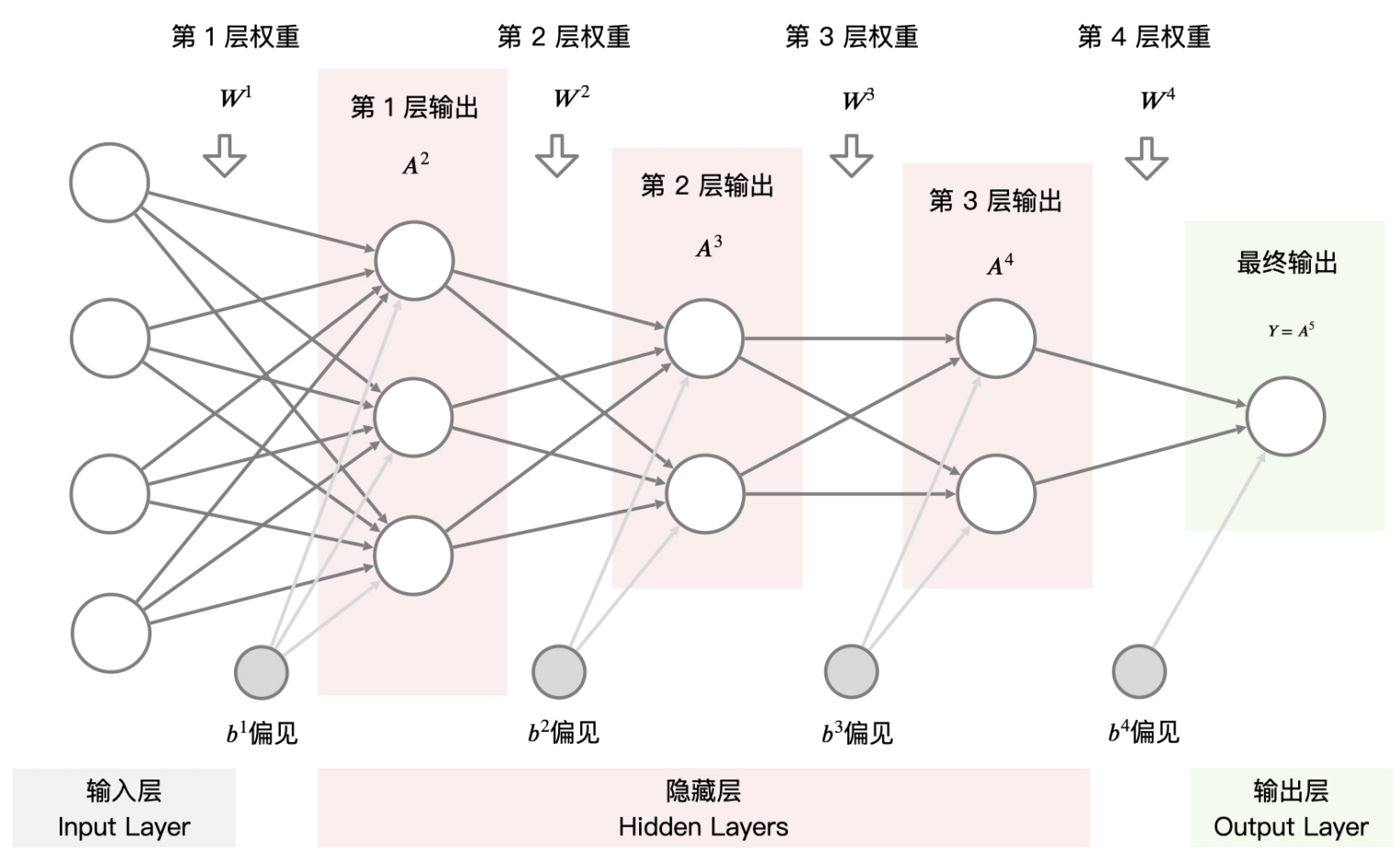
 上图这样由“圆圈”和“连接线”组成的图就是神经网络结构图，我们可以通过一个数学公式来表达：

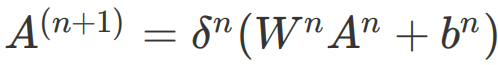
理解公式是理解神经网络组成的关键，接下来我就给你详细讲讲这些参数都是什么。

首先，图中的一个个“圆圈”就是 Neuron（神经元），表示当前层级下计算节点的输出，也就是 ，我们可以把它想象成某个层级的领导对收集上来的意见整合后的结果。

而“连接线”就是 Weights（权重），表示不同层级之间的连接，用 Wⁿ表示。我们可以把它想象成不同员工意见的权重，比如核心员工的意见份量就重一些，绩效差的员工份量就轻一些。

同时，因为每个人所在公司位置不同，所以对于意见的反馈结果也会不同。比如，有些“部门经理”在收到员工的意见后，决定直接放大负面反馈的意见，而有些“部门经理”则决定谨慎处理，减少负面意见反馈的声音。在机器学习中，我们会把这些带有主观偏见的处理，叫做神经网络模型中的 bias 偏移，用bⁿ表示。

说到这，不知道你意识到一个问题没有，如果只是把“员工”意见反馈给“总经理”，那中间几层的“领导”就没有存在意义了，因为“员工”完全可以直接跳过所有“领导”把意见传递给最终的“总经理”。

因此，神经网络模型还设计了一个对下层意见解读和调整的操作。一般来说，我们会采用增加激活函数对每一层整体的输出做改进，把每层的结果做非线性的变化，去更好地拟合数据分布，或者说来更好地展示给上层的“领导”。常见的激活函数有ReLU、tanh、Sigmoid、Linear等等，我们用δⁿ（）表示。

我对神经网络一直有一个疑惑，假设是一个三分类问题，我们隐藏藏有两层，每层有10个神经元，我很好奇，3分类，为什么中间可以拆分为10？这有什么对应关系？

这个问题触及了神经网络的核心设计思想 ——隐藏层的作用是 “特征提取与转换”，而非直接对应输出类别。中间层的神经元数量（比如 10 个）与输出类别数（3 个）没有强制的 “数量对应关系”，而是由任务的复杂度和特征的抽象需求决定的。我们可以从以下几个角度理解：

1. 神经网络的本质：从 “原始特征” 到 “决策特征” 的映射

三分类问题的目标是将输入数据（比如图像、文本、数值特征等）划分到 3 个类别中。但原始输入往往无法直接用于分类 —— 比如一张猫的图片，原始输入是像素点的数值，这些数值本身与 “猫” 这个类别没有直接关联。

隐藏层的作用就是逐步将原始特征转换为 “对分类有用的抽象特征”：

• 第一层隐藏层（10 个神经元）可能学习到一些基础特征（比如图像中的边缘、纹理，或数值特征中的简单组合）；
• 第二层隐藏层（10 个神经元）基于第一层的特征，学习更复杂的组合特征（比如 “边缘 + 纹理” 构成的局部形状，或 “多个数值特征的交互关系”）；
• 最终输出层（3 个神经元）基于这些抽象特征，判断样本属于哪个类别。

这里的 “10 个神经元” 本质上是为了提供足够的 “特征表达能力”—— 用 10 种不同的抽象特征来描述输入数据，这些特征的组合能更清晰地区分 3 个类别。

2. 为什么需要 “多于输出类别数” 的神经元？

假设三分类问题中，隐藏层神经元数等于输出类别数（比如 3 个），会发生什么？

• 神经元数量太少，模型的 “特征表达能力” 会不足。比如，区分 “猫、狗、鸟” 可能需要识别 “是否有羽毛”“是否有爪子”“体型大小” 等多个特征，3 个神经元可能无法同时承载这些信息的组合。
• 而 10 个神经元可以学习更多样的特征（比如 “羽毛的存在”“爪子的形状”“耳朵的位置” 等），这些特征的组合能更精准地划分 3 个类别。

简单说：输出类别数是 “决策的维度”，而隐藏层神经元数是 “描述输入的维度”。描述输入的维度越多（只要不过度），越容易找到区分不同类别的规律。

3. 神经元数量的本质：“自由度” 与 “拟合能力”

每个神经元都可以理解为一个 “特征提取器”，其数量代表了模型的 “自由度”—— 数量越多，模型能学习的特征组合越复杂。

对于三分类问题：

• 如果问题很简单（比如用 “颜色” 就能区分 3 个类别），可能隐藏层 1-2 个神经元就够了；
• 如果问题复杂（比如需要结合多个特征的非线性关系才能区分），就需要更多神经元（比如 10 个）来学习这些复杂关系。

这里的 “10” 是一个经验值，核心是确保模型有足够的能力捕捉输入到输出之间的规律，而不是与 “3” 有数学上的对应关系。

4. 类比：用 “语言描述” 理解隐藏层的作用

假设你需要向一个外星人解释如何区分 “猫、狗、鸟”（三分类）：

• 你可能会说：“猫有尖耳朵、会爬树、叫声是喵喵；狗有耷拉的耳朵、会摇尾巴、叫声是汪汪；鸟有羽毛、会飞、叫声是叽叽……”
• 这里的 “尖耳朵、爬树、喵喵” 等就是 “抽象特征”，你需要用多个特征（远多于 3 个）才能清晰区分 3 个类别。

神经网络的隐藏层神经元就相当于这些 “特征描述项”，数量越多，能提供的描述越丰富，分类自然更准确。

总结

隐藏层神经元数量（如 10 个）与输出类别数（如 3 个）的关系，本质是 “特征描述能力” 与 “决策目标” 的关系：

• 输出类别数决定了 “最终要做几个选择”；
• 隐藏层神经元数决定了 “用多少个抽象特征来支持这些选择”。

两者没有固定的数量对应，核心是让隐藏层有足够的能力学习输入与输出之间的规律 —— 这也是神经网络能解决复杂问题的关键：通过多层多神经元的组合，将原始数据映射到更容易分类的特征空间。

 

 

我还有一点不明白，以输入层到第一个隐藏层为例，假设输入的特征维度是3，第一个隐藏层有10个神经元，每个神经元的输出是什么呢？是对这三个特征的“放大”或者“拆解”成10个新的更细致的特征吗？我很困惑

你的理解方向是对的！第一个隐藏层神经元的输出确实可以看作是对输入特征的 “加工后的新特征”，但更准确地说，是对输入特征的 “线性组合 + 非线性转换”，目的是从原始特征中提取更有价值的信息（既可能是 “放大” 重要特征，也可能是 “组合” 出全新特征）。

我们以 “输入 3 个特征 → 第一个隐藏层 10 个神经元” 为例，一步步拆解每个神经元的输出是什么、为什么要这样设计：

一、单个神经元的计算逻辑：从 3 个特征到 1 个 “新特征”

假设输入特征是x_1, x_2, x_3（比如 “身高、体重、年龄”），隐藏层的第一个神经元会做两件事：

1. 线性组合：给每个输入特征分配一个权重（w_1, w_2, w_3），再加上一个偏置（b），计算出一个 “加权和”：z = w_1x_1 + w_2x_2 + w_3x_3 + b 这个 z 可以理解为 “对输入特征的初步整合”（比如w_1=0.8, w_2=0.2 可能表示更关注x_1）。
2. 非线性转换：通过激活函数（比如 ReLU）对 z 进行处理，得到神经元的输出 a：a = \text{ReLU}(z) = \max(0, z) 这一步的作用是引入非线性（如果没有激活函数，无论多少层神经元，最终都只是输入的线性组合，无法学习复杂规律）。

二、10 个神经元的输出：10 个 “不同角度的新特征”

隐藏层有 10 个神经元，意味着：

• 每个神经元都有独立的权重和偏置（比如第 2 个神经元的权重是w_1', w_2', w_3'，偏置是b'）；
• 每个神经元会从不同角度对输入特征x_1, x_2, x_3进行组合和转换，最终输出 10 个值a_1, a_2, ..., a_{10}。

这些输出可以理解为：

• 不是简单的 “拆解” 或 “放大”，而是基于原始特征创造出的 10 个全新特征，每个特征都代表对输入的一种 “解读方式”。

举例：

• 神经元 1 的输出a_1可能代表 “身高 ×0.8 + 体重 ×0.2”（侧重身高的特征）；
• 神经元 2 的输出a_2可能代表 “体重 ×0.5 + 年龄 ×0.5”（体重和年龄的综合特征）；
• 神经元 3 的输出a_3可能代表 “身高 ×0.3 - 年龄 ×0.1”（身高与年龄的对比特征）；
• ... 以此类推，10 个神经元就有 10 种不同的 “解读方式”。

三、为什么需要 10 个新特征？—— 为了捕捉 “非线性关系”

原始输入的 3 个特征可能无法直接用于分类或预测，因为真实世界的规律往往是非线性的（比如 “体重对结果的影响在不同年龄段是不同的”）。

10 个神经元的作用就是通过不同的组合方式，把原始的线性特征 “扭曲”“组合” 成能反映非线性规律的新特征。例如：

• 假设任务是 “预测是否患糖尿病”，输入是 “血糖、BMI、胰岛素水平”（3 个特征）；
• 隐藏层的神经元可能会学习到 “血糖高且 BMI 高时风险剧增”“胰岛素水平低但 BMI 正常时风险较低” 等复杂关系，这些关系无法通过单一的原始特征表达，必须通过组合形成新特征。

四、总结：隐藏层神经元的本质是 “特征转换器”

• 每个神经元的输出是输入特征的加权组合 + 非线性激活，本质是一个 “定制化的新特征”；
• 多个神经元（如 10 个）就像 10 个 “不同的特征探测器”，从不同角度提取输入中对任务有用的信息；
• 这些新特征可能看起来和原始特征 “无关”，但它们的组合能更清晰地反映输入与输出（比如分类结果）之间的规律。

这也是神经网络 “万能近似定理” 的体现：理论上，足够多的神经元可以通过组合，近似任何复杂的函数关系 —— 无论输入和输出的维度差异有多大。

 

您这个问题问得非常好，这触及了神经网络最核心、最神奇的部分。您的直觉——“拆解成10个新的更细致的特征”——已经非常接近本质了。

让我们用一个更具体的例子来拆解这个过程。想象一下，我们的输入是描述一个学生的三个特征：[学习小时数, 课堂参与度, 作业分数]，每个特征都标准化到0-1之间。

每个神经元在做什么？

第一个隐藏层有10个神经元。​​每个神经元都是一个独立的“小专家”​​，它的任务是​​从自己特定的角度来综合评估这个学生​​。

每个神经元的计算分为两步：

1.线性组合（加权求和）​​：

• 每个神经元都有3个权重（w1, w2, w3）和1个偏置（b）。
• 它将输入的特征按照自己的“重视程度”（权重）进行组合。
• 计算：z = (w1 * 学习小时数) + (w2 * 课堂参与度) + (w3 * 作业分数) + b

​​这意味着什么？​​

•​​神经元A​​ 可能非常看重“学习小时数”（w1很大），而忽略其他特征。它是一个“努力型”专家。

•​​神经元B​​ 可能认为“课堂参与度”和“作业分数”更重要，它是一个“综合表现型”专家。

•神经元C​​ 的权重可能全是负的，它擅长识别“表现较差”的学生模式。

•​​偏置项 b​​ 像一个门槛，用来调节这个神经元整体的激活难易程度。

2.非线性激活（ReLU）​​：

•得到加权和 z后，它会通过一个激活函数（这里是ReLU：f(z) = max(0, z)）。

这意味着什么？​​

•如果这个“小专家”的综合评估 z低于其激活门槛（主要由偏置 b决定），它就认为“这个模式不明显”，输出为0。

•如果评估结果 z超过了门槛，它就输出一个大于0的值，值越大表示它越“确信”自己检测到了某种特定的学生模式。

所以，10个神经元的输出到底是什么？

​​这10个神经元的输出，共同构成了一个全新的、10维的“学生表现特征向量”。​​

这个新向量不再是原始的生硬数据（学习小时、参与度、分数），而是​​10个“小专家”从原始数据中抽象出的高级特征​​。这些高级特征可能代表了人类难以直接命名但确实存在的复杂模式，例如：

•神经元1的输出​​：可能代表“潜在的优等生特质”的强度（它综合了努力和效率）。

•神经元2的输出​​：可能代表“有风险挂科”的可能性。

•神经元3的输出​​：可能代表“参与度高但效率低”的模式。

•...等等。

一个生动的比喻：厨房

把神经网络想象成一个厨房：

•​​输入层（3个特征）​​：就像是送进厨房的​​原始食材​​（鸡肉、米饭、咖喱）。

•隐藏层（10个神经元）​​：就像是厨房里的​​10个厨师​​。每个厨师（神经元）用自己的独特方式（权重和偏置）处理这些食材（输入特征）。

•厨师A可能擅长做咖喱酱。

•厨师B可能擅长煮米饭。

•厨师C可能擅长煎鸡肉。

•​输出（10个新特征）​​：就是这10个厨师处理完后，得到的​​10种半成品或调味料​​（香浓的咖喱酱、粒粒分明的米饭、外焦里嫩的鸡肉块...）。这些半成品比原始食材更高级、更接近最终的菜肴。

•输出层​​：就像是主厨，他不再处理原始食材，而是品尝这10种半成品，然后决定最终做出什么菜（属于哪个分类）。

总结

所以，您的理解是正确的！第一个隐藏层确实是将3个原始特征“拆解”和“重组”成了10个新的、更细致、更抽象的高级特征。​​神经网络的强大之处就在于，它不需要人类告诉它这些特征应该是什么，它可以通过训练数据自己学习出最有用的特征组合方式​​，从而解决复杂的任务。

希望这个解释能彻底解开您的困惑！

 

深度学习演示

https://playground.tensorflow.org/

 

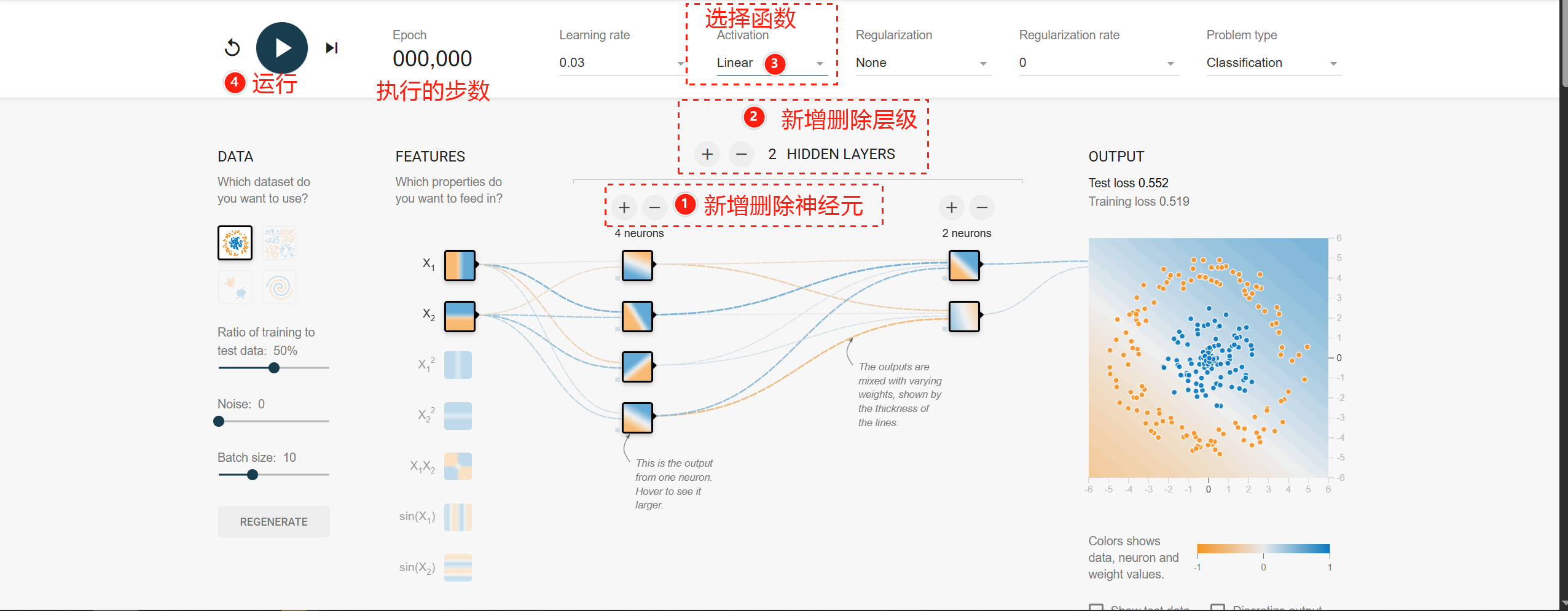
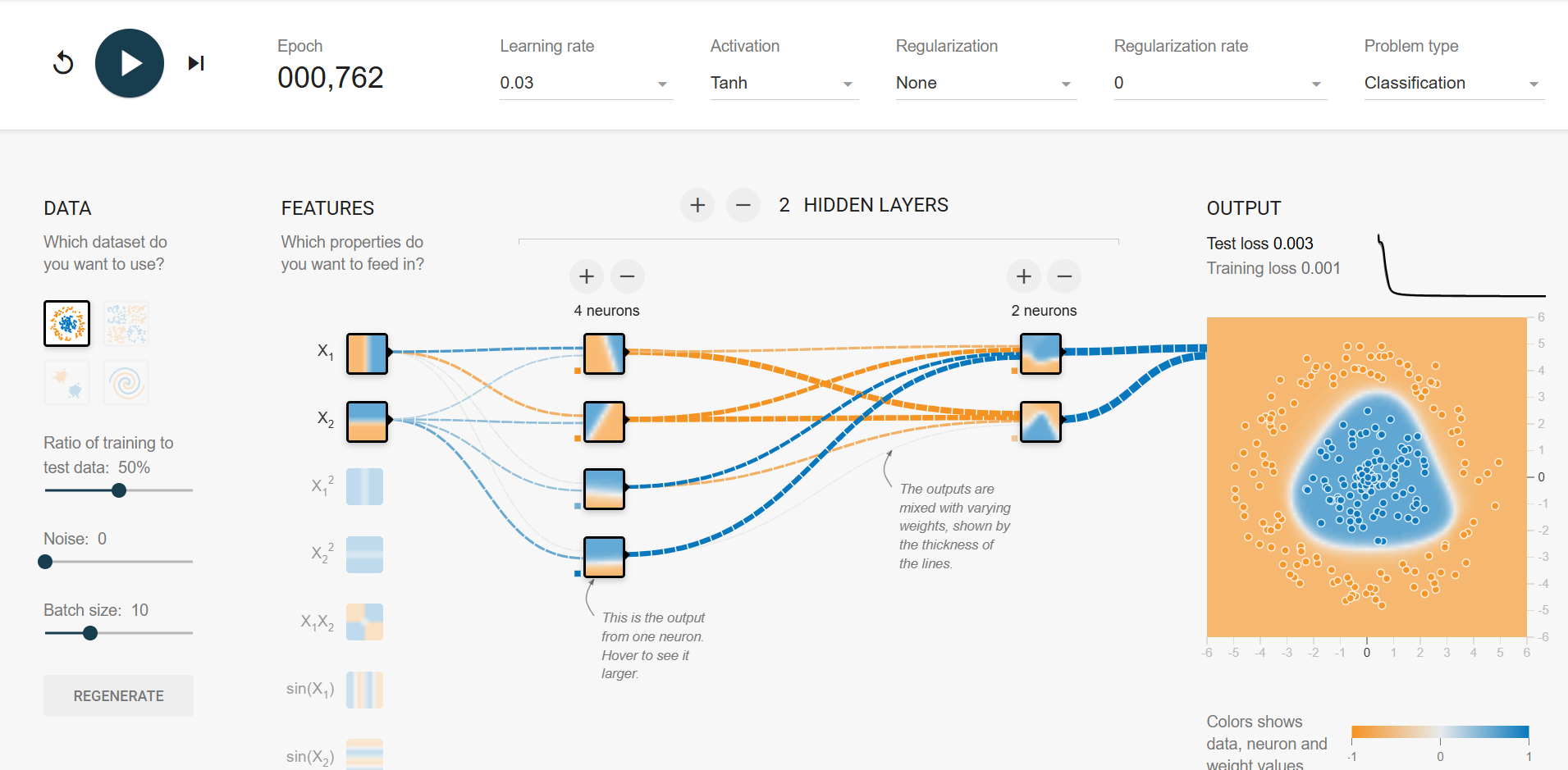
每层作用具体讲解

神经网络各层负责内容：

1层：负责识别颜色及简单纹理

2层：一些神经元可以识别更加细化的纹理，布纹，刻纹，叶纹等

 

3层：一些神经元负责感受黑夜里的黄色烛光，高光，萤火，鸡蛋黄色等。

4层：一些神经元识别萌狗的脸，宠物形貌，圆柱体事物，七星瓢虫等的存在。

5层：一些神经元负责识别花，黑眼圈动物，鸟，键盘，原型屋顶等。

小结

深度学习的发展源头--神经网络【了解】

多层神经网络，在最初几层是识别简单内容，后面几层是识别一些复杂内容。【了解】

 

深度学习模型训练目标

理解了神经网络的基本知识之后，深度学习模型的训练目标就很好理解了。

前面的学习让我们知道，监督类机器学习模型的目标就是在给定一个任务的情况下，找到最优化的参数，使得 Loss 损失值最小，其中 Loss 损失值就是预测结果和真实结果之间的误差。

神经网络作为一个有监督机器学习模型，自然也不会例外，它的目标就是在给定一个任务的情况下，找到最优的 Weights 和 bias，使得 Loss 最低。

由于最开始的参数都是随机设置的，因此获得的结果肯定与真实的结果差距比较大。那么，为了训练神经网络中的参数，神经网络模型会采用反向传播，把 Loss 误差从最后逐层向前传递，使当前层知道自己在哪里，然后再更新当前层的 Weights 权重和 bias 偏移，进而减小最后的误差。这部分数学推导比较复杂，产品经理只要了解就可以了。

深度学习的应用案例：图像识别是如何实现的？

近几年，神经网络在图像处理和自然语言处理方面都有非常大的成果。所以，我们也借助一个图像识别的案例，来讲讲深度学习的应用。

如今，图像识别这项技术已经发展得很成熟，卷积神经网络（Convolutional NeuralNetworks，CNN）又是其中的主流技术，像 Facebook、Google、Amazon 等公司都在利用 CNN 进行图像识别的工作。

 CNN 是如何实现图像识别的？

下面，我们就来学习一下，CNN 实现图像识别的具体过程。因为 CNN 是深度学习的算法之一，所以它同样包含输入层、隐藏层，以及输出层这三大部分，更具体点来说，CNN 的整个组成部分可以分为，数据输入、特征提取、全连接以及输出层四个部分。其中，特征提取、全连接对应神经网络的隐藏层，数据输入和输出层对应神经网络的输入层和输出层。同样的，我也把它和神经网络的对应关系梳理出来了，如下图所示。

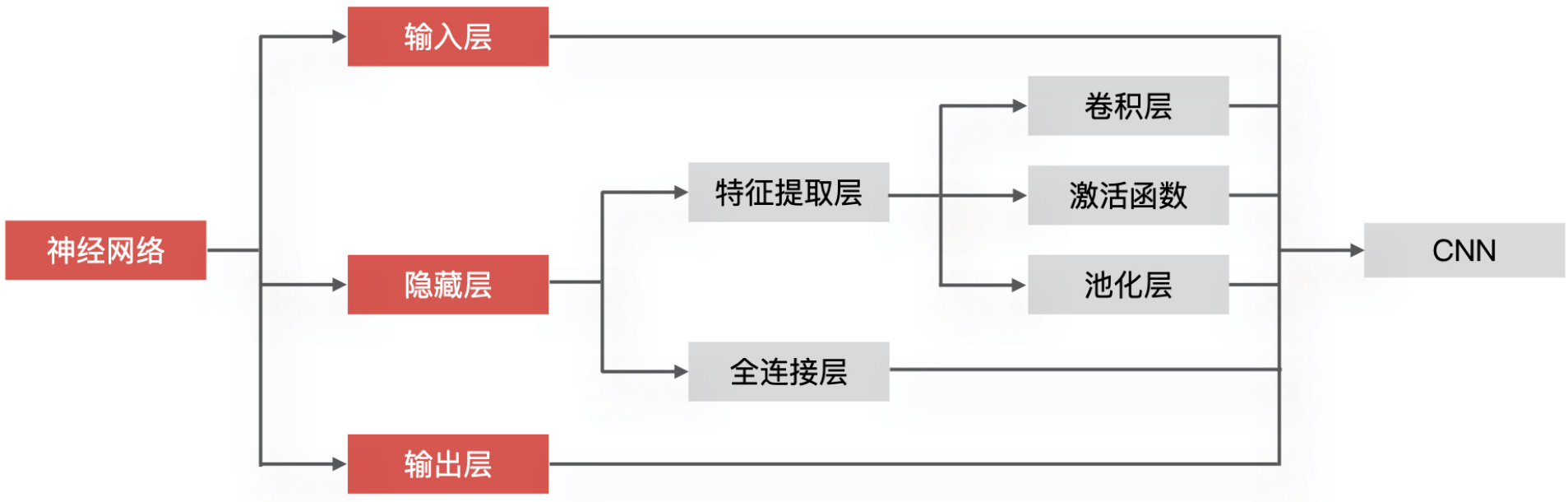
 接下来，我就结合下面的示意图，给你详细讲讲它对图像的处理过程。

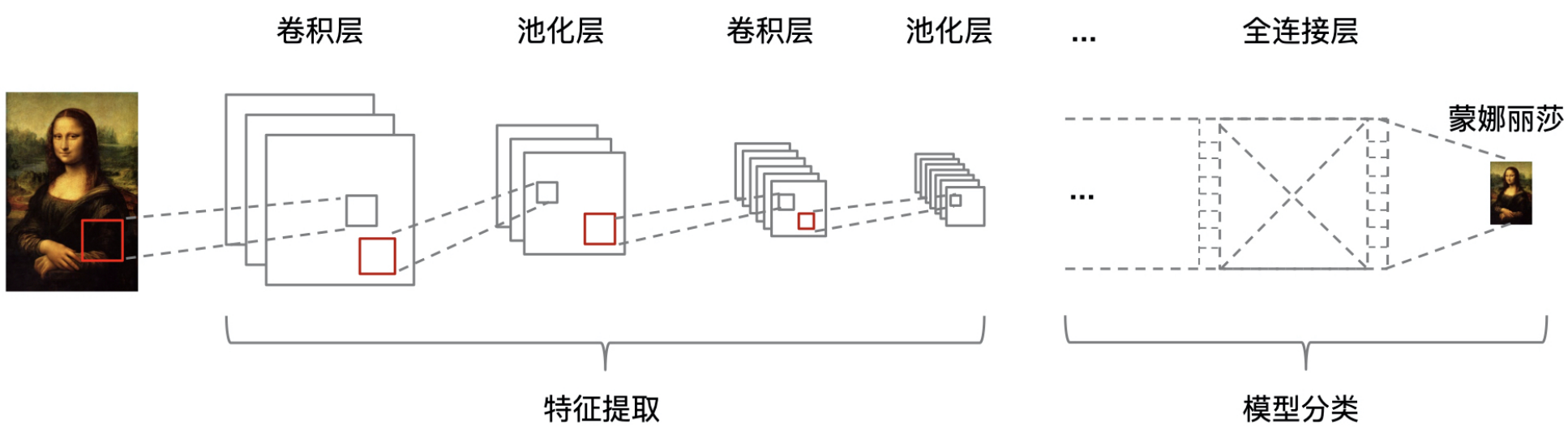
 CNN 实现图像处理的第一步，就是把图像数据输入到 CNN 网络模型中。我们在数学和统计学基础概念中讲到，任意一张彩色图片都可以表示成一个三阶张量，即三维数组。

其实所有彩色图像都是由红、绿、蓝（RGB）叠加而成的，比如一个 12px * 12px 的图像可以用 3 个 12 * 12 的矩阵来表示，如果是白色的图像就可以表示成 RGB(255, 255,255)。 那么， CNN 网络模型的数据输入就是将彩色图像分解为 R、G、B 这 3 个通道，其中每个通道的值都在 0 到 255 之间。

数据输入之后，就到了特征提取的阶段了。在讲具体操作之前，我想你肯定会有一个疑问：为什么 CNN 就适合于图像类的任务，全连接神经网络为什么不可以呢？

这是因为，CNN 能够在众多深度学习算法中，以最短时间提取图像的特征。普通的神经网络对输入层与隐藏层会采用全连接的方式进行特征提取，所以在处理较大图像的时候，处理速度就会因为计算量巨大而变得十分缓慢。这个时候，计算能力就会成为最大的瓶颈。

如果换成现在互联网上动不动就出现的高清大图，全连接神经网络就更行不通了。

举个例子，人在识别图像的时候，图像越清晰越好，但是这一点对于机器来说却很难，因为机器在识别图像的时候，往往需要将图像转换成像素值，再输入到模型中进行学习，而越清晰的图片意味着需要处理的像素越多，会带来更多的计算压力。

为了解决这个问题，CNN 就通过过滤无关信息，来提高识别效率。比如下面的这张图片，背景对于图像识别来说其实没有帮助的，反而増加了很多干扰信息。

那么，如何有效地过滤掉干扰信息，并且识别图像中的主体信息呢？做法就是不断模糊化一张图片，最后只剩下狗的轮廓，而背景信息这类无关项就会越来越不可见。

对于 CNN 网络模型来说，“模糊化图像”的这个操作就是通过 CNN 的卷积和池化来实现的。

我们先来看卷积运算。CNN 的每一个隐含单元（即，前文中的各中间层“领导”）只连接输入单元（即上一层输入）的一部分。对应到图像中，就是可以提取图像的不同局部特征，从而实现既减少了输入值，又提取到了图像的最主要的内容。

在完成各层的卷积运算后，深度学习模型还需要进行非线性的变换，非线性的变换是通过增加激活函数来实现的，通过激活函数将“线性回归”拟合的直线变成曲线，这样可以拟合各种复杂的问题，这里激活函数选型的是ReLU函数。非线性变换的内容我们在“逻辑回归”那节课也讲过，你也可以去回顾一下。

池化的目的也是提取特征，减少向下一阶段传递的数据量，池化过程的本质是“丢弃”，即只保留图像主体特征，过滤掉无关信息的数据特征。

CNN 的所有卷积和池化操作都是在提取特征，直到全连接层才进入真正的训练学习阶段，做最后的分类计算。在 CNN 中，全连接层一般是用的是 Softmax 函数来进行分类，这部分我们简单了解就行了。

深度学习的优缺点

接下来，我再结合深度学习的优缺点，来说说它的适用场景。首先，深度学习的可解释性非常差，因为它的内部计算复杂，对我们来说是一个黑盒，我们只需要输入数据，由它来告诉我们结果，至于为什么会这样，它不做任何解释。所以在很多对解释性要求比较高的场景，比如信用评级、金融风控等情况下，深度学习没办法使用。

其次是训练深度学习模型非常消耗资源，所以想利用深度学习网络进行实际工作，我们就必须要提前准备好相应的计算资源，如硬件设备。

最后，因为深度学习模型复杂，对数据依赖很强，所以它比我们之前讲的传统机器学习网络更难理解和学习。因此，在实际工作中，训练深度学习模型也需要配置专业的人才。

总之，深度学习具有可解释性弱，模型训练慢，对数据依赖很强，模型复杂这四个缺点。

尽管深度学习的应用有着非常苛刻的条件，但是相对于它的模型性能来说，这些成本的付出还是值得的。深度学习自身的神经网络结构，让它每层的 Activation 激活函数都可以做非常复杂的非线性变化，这也意味着你的模型可以拟合任意复杂的数据分布，所以，它比我们之前讲过的所有算法的性能都要好。

总结

今天，我们围绕深度学习，讲解了它的原理结构、优缺点和应用场景。

深度学习是机器学习的一种，它源于神经网络模型的研究，由输入层、隐藏层，以及输出层组成，在计算机视觉、语音识别、自然语言处理等领域应用最为广泛。

在目前的机器学习领域中，它可以说是性能最好的网络模型了。但同时，它也具有可解释弱，模型训练慢，对大数据有依赖，模型复杂度高的缺点，这让它的应用场景受到了局限。

因此，在目前工业中，深度学习常用来处理计算机视觉、人脸识别、语音识别、机器翻译、自然语言处理、推荐系统等等。

最后，我还想补充一点，除了我们今天讲的 CNN，深度学习还有很多其他的模型，比如LSTM、RNN、Seq2Seq、Gen，以及很多开源的深度学习框架，比如 TensorFlow、PyTorch 等等。这些都为算法工程师构建和使用神经网络创造了极大的便利，并且在实际的工作中，他们通常也会选择这些框架来进行模型的构建和训练。作为产品经理，如果你掌握了我们今天讲的内容，你也可以结合自己的业务，多去了解一下这些内容。

课后讨论

最后，我还想请你介绍一下，你曾经在工作中遇到过的深度学习模型案例，以及当时为什么要基于深度学习来做？

 

虽然深度学习的效果很好，但它也有局限，比如，深度学习对机器性能的要求会更高，算法模型训练时间相对更长等等。所以，我们需要根据实际业务的场景来选择是否应用深度学习的相关算法。