第四章学习小结

学习内容小结：

一、串

1、BF算法

　将模式串跟主串从开头一个一个比较，如果匹配失败，又从模式串第二个字符一次比较，匹配，++i；++j；不匹配，i=i-j+2；j=1;

　　一般情况下，BF算法时间复杂度为O（m*n），数据量不大时候，执行时间近似为O（m+n）,但如果是庞大数据，那它的效率就很低了，一个测试点主串长度100万，模式长度10万，而且是那种主串为aaaaaaaa...,模式串是ba......。所以，从第一个字符比较一直不匹配，而模式串一直回溯到j=0,这样工作量超大，所以上面BF算法提交之后在这个测试点是运行超时的。

2、KMP算法

以下见解是经历多方参考后的结果

首先是主串s 和模式串t 的比较，当前比较的是主串s的第i个和模式串的第j个，若s[i]==t[j]; 则++i; ++j; 这里i，j为位置，而非下标

当出现不匹配时，i不回溯（停留在当前位置），通过next数组找到下一个和s[i]比较的数的下标k；

由于模式串t的任一元素都有可能和s在匹配时，失配，所以要为t的每个元素找好一个“后备军”k 以应对t[j]和s[i]不匹配的情况。于是这里用next数组来存储这些"后备军“k，当s[i]!=t[j]，则j退到第二选择k，再进行s[i]和s[k]的比较

明显k不是随便的一个数，作为t[j]的“后备军”，满足：k之前的k-1个数和j前的k-1个数一一相等，只有这样t[k]才能而直接和当前已和t[i]失配的s[i]比较，而免去前k-1次和s的比较

设此时j的“后备军”为k，即next[j]=k，那么要求next[j+1]的值，则需要比较t[j]和t[k]的值，即比较t[j]和t[k]

若t[j]==t[k]，那么next[j+1]=next[j]+1；否则再退一步，比较t[j]和t[next[k]]直到比较到相等的，或比到最后的最后：t[j]!=t[1]，则next[j]=1

复制代码
void get_next(SString T, int next[])
{//求模式串T的next函数值并存入数组next
    i=1;next[1]=0;j=0;
    while(i<T.length)
    {
        if(j==0 || T.ch[i]==T.ch[j]
        {
            ++i;
            ++j;
            next[i]=j;
        }
        else
            j=next[j];
    }
}
复制代码

然而，以上函数然存在缺陷，例如在面对主串为“aaabaaaab",模式串为”aaaab“时，仍浪费了时间

于是改进为

复制代码
void get_next(sstring t,int Next[])  //求模式串t的next函数值并存入数组next 
{
    int i=1,j=0;
    Next[1]=0;
    while(i<t.length)
    {
        if(j==0 || t.ch[i]==t.ch[j])
        {
            ++i;
            ++j;
            if(t.ch[i]!=t.ch[j])
                Next[i]=j;
            else
                Next[i]=Next[j];
        }
        else
            j=Next[j];
    }
复制代码

不同的是，若当前比较时t.ch[i]!=t.ch[j]，则Next[i]的值再退一步到Next[j]的值

以下贴上两种代码

#include<iostream>
using namespace std;
#include<string.h>

//采用静态顺序存储结构（定长）
typedef struct{
    char ch[1000002];   //存储串的一维数组
    int length;     //串的长度
}SString;

SString S,T;

char s[1000002];
char t[1000002];
int nex[1000002];

//KMP算法
//查找 模式T 在 主串S 中第pos个字符开始第一次出现的位置，并返回
//若不存在，则返回0 （T非空，1<=pos<=S.length）
int Index_KMP(SString S,SString T,int next[]) 
{              
    int i,j;
    i=j=0;
    while(i<=S.length-1 && j<=T.length-1)
    {
        if(j==-1||S.ch[i]==T.ch[j]){    //从各自的第一位开始比较，如果相同，比较下一位
            ++i;
            ++j;
        }
        else {
            j=next[j];
        }
    }
    if(j>T.length-1)        //匹配成功
        return i-T.length+1;//
    else            //匹配失败
        return 0;
}

void get_next(SString T,int next[]){
    int i=0;
    next[0]=-1;
    int j=-1;
    while(i<T.length-1){
        if(j==-1||T.ch[i]==T.ch[j]){
            ++i;
            ++j;
            next[i]=j;
         }
         else {
            j=next[j];
         }
     }
}
//主函数
int main()
{
    cin>>s>>t;
    strcpy(S.ch,s);
    strcpy(T.ch,t);
    S.length=strlen(S.ch);
    T.length=strlen(T.ch);
    get_next(T,nex);
    cout<<Index_KMP(S,T,nex)<<endl;
    return 0;
}

 

PTA作业的另一种代码：

#include <iostream>
#include <string.h>
using namespace std;

//定义从1开始存放的串结构
typedef struct {
    char ch[1000002] = { " " };
    int length;
}SString;

void Read(SString &S, char temp[]);
void getNext(SString T, int next[]);
int KMP(SString S, SString T, int next[]);

SString S, T;
char temp[1000002] = { " " };
int Next[1000002] = { 0 };

int main() {
    int result = 0;     //result为结果，即T在S中第一个出现的位置，没有出现则为0
    cin >> temp;
    Read(S, temp);
    cin >> temp;
    Read(T, temp);
    getNext(T, Next);
    result = KMP(S, T, Next);
    cout << result;
    return 0;
}

//先让模式串自我比较得出next数组，因为数组实际上是首地址，所以可以用void类函数且不引用
void getNext(SString T, int next[]) {
    int i = 1, j = 0;   //j表示最长串的最后一个，i进行遍历
    next[1] = 0;
    while (i < T.length) {
        if (j == 0 || T.ch[i] == T.ch[j]) {     //j=0表示没有相同串，ch[i] = ch[j]表示如果相同那么没有必要右移模式串
            i++;
            j++;
            if (T.ch[i] != T.ch[j]) {   //i和j都右移后如果不同，是正常情况，直接把最长串最后一个的位置给next
                next[i] = j;
            }
            else {                      //但是如果相同，就让next变为next[j]，因为next[j]是之前已经得到的最长串最后一个的位置
                next[i] = next[j];
            }
        }
        else {                  //如果j不为0且ch[i] 与 ch[j]不等，表示之前有相同串，但是现在右移了导致之前的相同串不相同了，说明之前得出的相同串已经废了，于是重置j
            j = next[j];
        }
    }
    return;
}

int KMP(SString S, SString T, int next[]) { //S主串，T模式串
    int i = 1, j = 1;       //i指主串，j指模式串
    int result = 0;
    while (i <= S.length&&j <= T.length) {
        if (j == 0 || S.ch[i] == T.ch[j]) {     //如果匹配接着往下比较，不匹配就右移T
            i++;
            j++;
        }
        else {
            j = next[j];
        }
    }
    if (j > T.length) {     //当且仅当j到最后仍与主串相等+1时匹配成功
        result = i - T.length;
    }
    return result;
}

void Read(SString &S, char temp[]) {    //将输入的字符串接在S后面
    S.ch[0] = ' ';
    strcat(S.ch, temp);
    S.length = strlen(S.ch) - 1;
    return;
}
 
二，数组
在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵。
为了更好地定义稀疏矩阵，引入稀疏因子 t =num/(n*m)[其中num为矩阵中非零元素个数，n为矩阵行数，m为矩阵列数]，
当t<=0.05时，该矩阵即可称作稀疏矩阵。


压缩稀疏矩阵的常见方法有两种：
1.利用三元组表压缩
  优点：①代码简易；
       ②占用空间相对较小
  缺点：①无法实现随机存储；
       ②在进行对矩阵的操作（如矩阵的乘法/加法）矩阵中数据改变后，需要重新定义三元组表，不具有通用性，不灵活。

2.利用十字链表压缩
  优点：①能够实现随机存储；
       ②对于任意矩阵具有通用性
  缺点：①代码实现困难；
       ②占用空间相对较大

十字链表（Orthogonal List)是有向图的另一种链式存储结构。该结构可以看成是将有向图的邻接表和逆邻接表结合起来得到的。

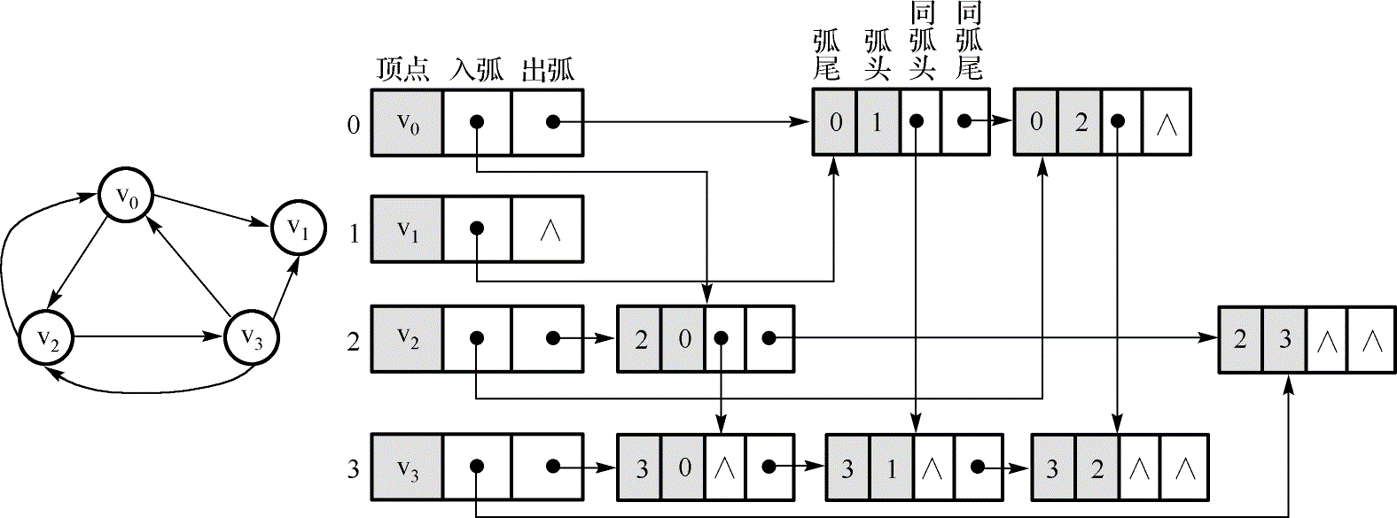
  • 入弧和出弧：入弧表示图中发出箭头的顶点，出弧表示箭头指向的顶点。
  • 弧头和弧尾：弧尾表示图中发出箭头的顶点，弧头表示箭头指向的顶点。

  • 同弧头和同弧尾：同弧头，弧头相同弧尾不同；同弧尾，弧头不同互为相同。

    心得体会：
    打代码的时候要尽力远离书本，上次小测成绩不理想完全是因为在之前耗费的时间太多了，以至于剩下了最后一道很简单的题目orz。
    又很多情况下都是思维想好了但不能转化成正确的能跑起来的代码，归根结底还是打代码能力的不足吧

posted on 2019-04-14 15:50  陆佑蓝  阅读(304)  评论(1)    收藏  举报

导航