Matlab 设计仿真CIC滤波器
2023.09.26
使用CIC滤波器用于降采样。同样的,CIC滤波器也适用于升采样。
参考连接:
[1] Matlab中CIC滤波器的应用_dsp.cicdecimator_张海军2013的博客-CSDN博客
[2] Matlab中CIC滤波器的应用 - 知乎 (zhihu.com)
[3] CIC filter及其matlab实现-CSDN博客
[4] 【ljelly原创】 Matlab实现抽取滤波器的设计(CIC) – MATLAB中文论坛 (ilovematlab.cn)
[5] 基于CIC抽取滤波器设计与实现 - 知乎 (zhihu.com)
进行CIC降采样滤波器设计,实现采样率从50kSPS降至2kSPS,25倍降采样。简单分析:要实现25倍降采样率,可以通过使用2个5倍降采样率的CIC串联实现,也可以使用1个25倍降采样率的CIC实现。具体分别使用几级滤波器需要按照需求和硬件支持调整,此处以常见和通用的3级CIC滤波器为例进行设计。
CIC滤波器的系统函数为
其中,\(M\) 为CIC滤波器长度,也是CIC滤波器的升/降采样倍率;\(N\) 为CIC滤波器级数。那么,其频率响应为
关于CIC数字滤波器的基本知识此处不做过多介绍,后续有计划会整理相关内容。
1. 使用函数设计
在Matlab中,有两个函数可以生成CIC滤波器。我们以CIC抽取滤波器为例,一个是fdesign.decimator,第二个是dsp.CICDecimator。详细用法在上述参考链接[1]中有说明 。
下面使用 fdesign.decimator() 函数设计5倍降采样率CIC
%-------------------------------------------------------
% 参数设置
Fs = 50e3; % sample rate
R = 5; % decimator factor
D = 1; % differential delay
Fp = 4e3; % pass band
Fstp = 5e3; % stop band
Ap = 0.1; % attenuation in pass band
Astp = 40; % attenuation in stop band
%-------------------------------------------------------
%-------------------------------------------------------
% 设计方法1: 设计单位增益CIC滤波器
d1 = fdesign.decimator(R,'cic',D, Fp, Astp, Fs);
hcic = design(d1);
H1 = cascade(1/gain(hcic),hcic);
d2 = fdesign.ciccomp(hcic.DifferentialDelay, ...
hcic.NumberOfSections,Fp,Fstp,Ap,Astp,Fs/R);
cic_comp = design(d2);
%--------------------------------------------------------
%-------------------------------------------------------------------------------
% 设计方法2: 设计未做单位增益CIC滤波器
% hcic = design(fdesign.decimator(R,'cic',D, Fp, Astp, Fs),'SystemObject',true);
% cic_comp = design(fdesign.ciccomp(hcic.DifferentialDelay, ...
% hcic.NumSections,Fp,Fstp,Ap,Astp,Fs/R), 'SystemObject',true);
%-------------------------------------------------------------------------------
fvtool(H1,cic_comp,cascade(H1,cic_comp),'ShowReference','off','Fs',[Fs Fs/R Fs]) % 未做归一化处理
legend('CIC Decimator','CIC Compensator','Resulting Cascade Filter');
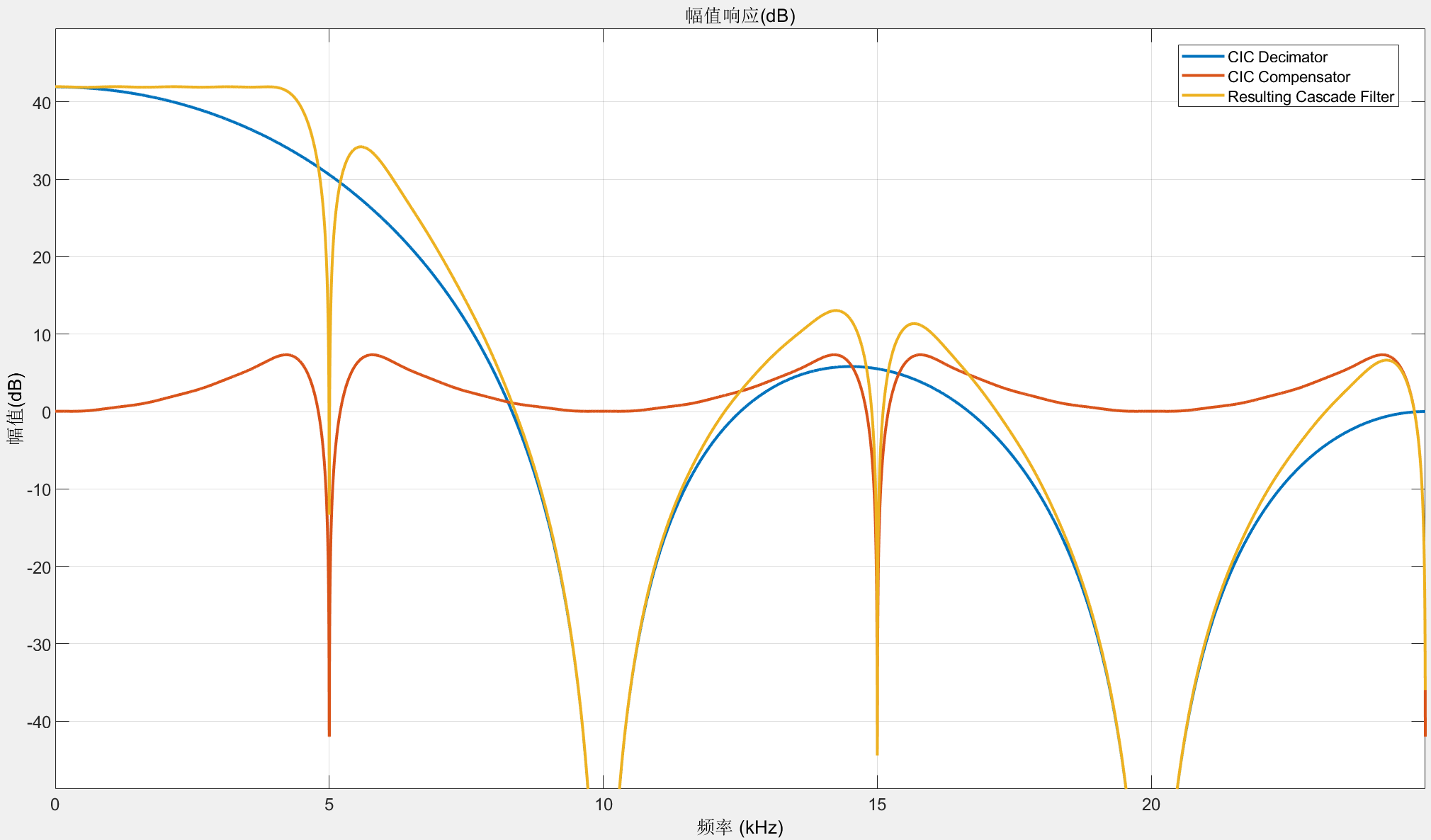
下面使用 dsp.CICDecimator 函数设计5倍降采样率CIC
Fs = 50e3; % sample rate
R = 5; % decimator factor
D = 1; % differential delay
N = 3; % number of stage
Fp = 0.05; % pass band
Fstp = 0.075; % stop band
Ap = 0.1; % attenuation in pass band
Astp = 60; % attenuation in stop band
CICDecim = dsp.CICDecimator(R, D, N);
CICCompDecim = dsp.CICCompensationDecimator(CICDecim, ...
'DecimationFactor',2,'PassbandFrequency',Fp, ...
'StopbandFrequency',Fstp,'SampleRate',Fs/R);
fvtool(CICDecim,CICCompDecim,...
cascade(CICDecim,CICCompDecim),'ShowReference','off','Fs',[Fs Fs/R Fs])
legend('CIC Decimator','CIC Compensator','Resulting Cascade Filter');
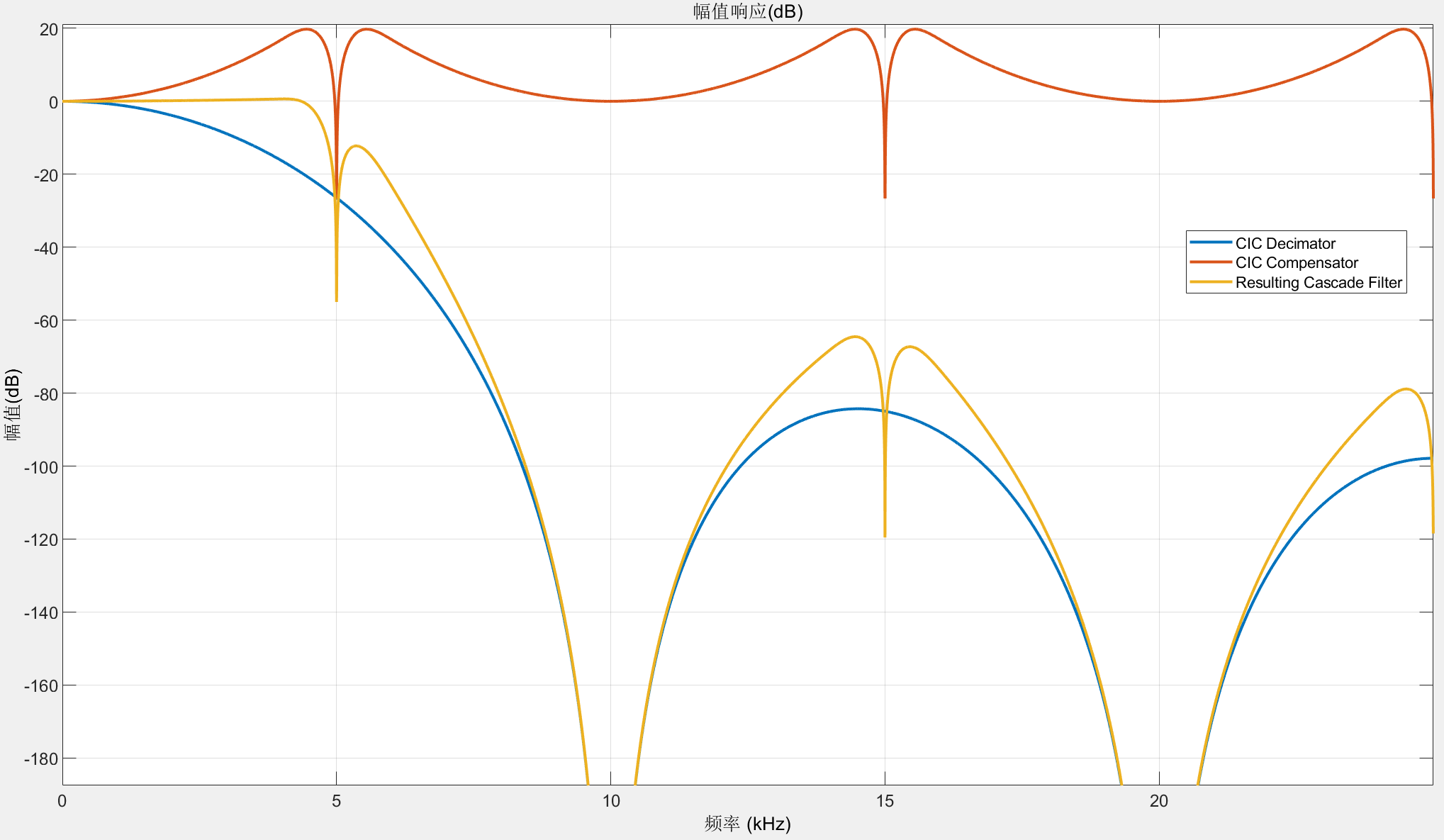
2. 使用工具箱设计
打开 filterDesigner 工具箱,两种方式:
- matlab 命令行输入
>> filterDesigner回车; - matlab 主界面顶部
APP选项卡,搜索 filterDesigner 打开。
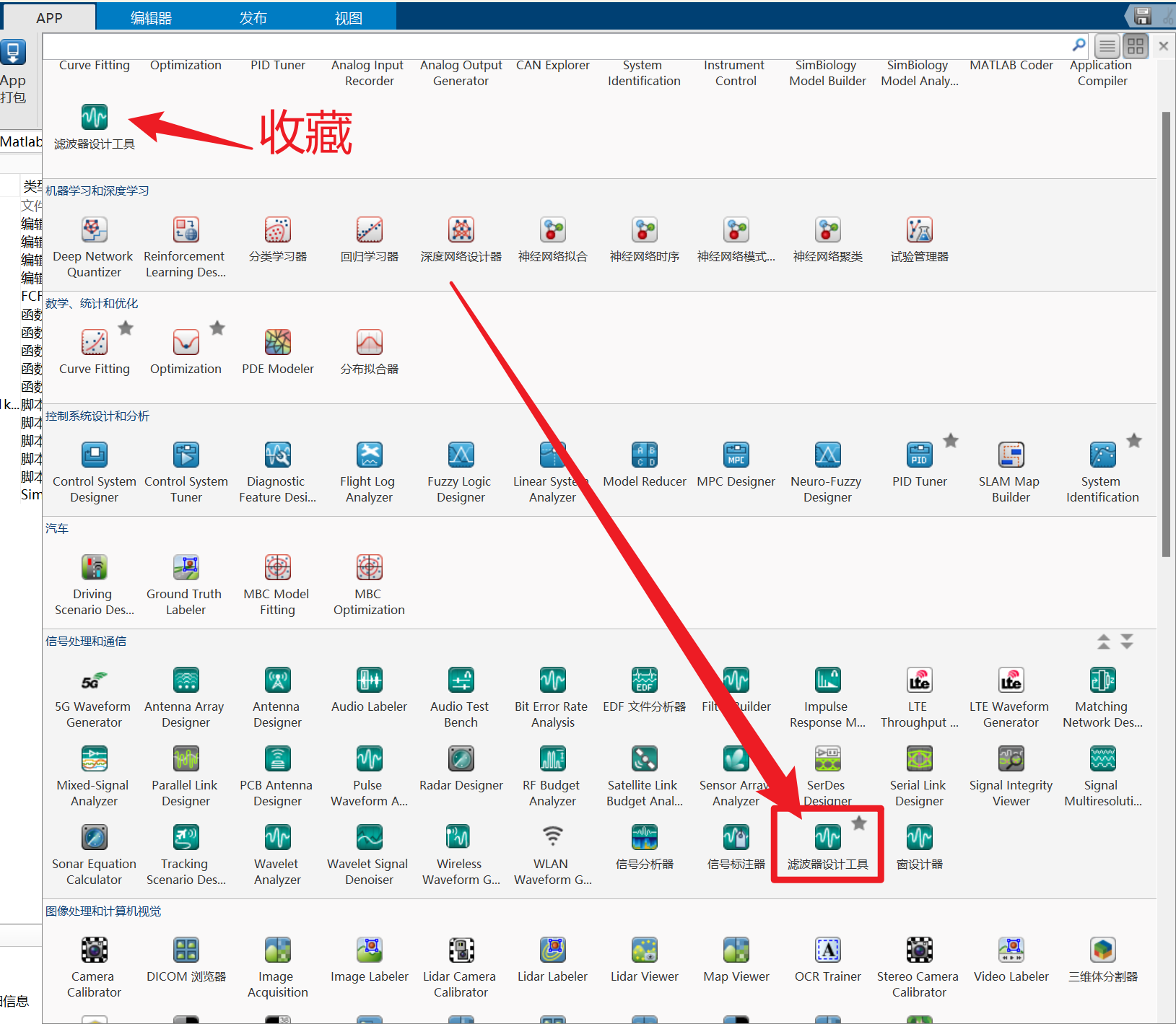
打开后,进行CIC抽取滤波器设计:
- 主界面选择 :
创建多速率滤波器 - 类型选择:
抽取器 - 选择使用滤波器类型:
级联积分梳妆(CIC)滤波器 - 设置抽取因子:
5(示例) - 设置采样频率: 归一化与采样率都可以
- 设置积分延迟和节数(级数): 延迟一般设计为
1节数(级数)设计:3 - 选择频响显示样式
- 创建滤波器
- 设计信息展示于左上角
- 定点化设计:根据带滤波信号的数据范围进行滤器定点化设计,特别是滤波器级联使用时
设计界面展示:
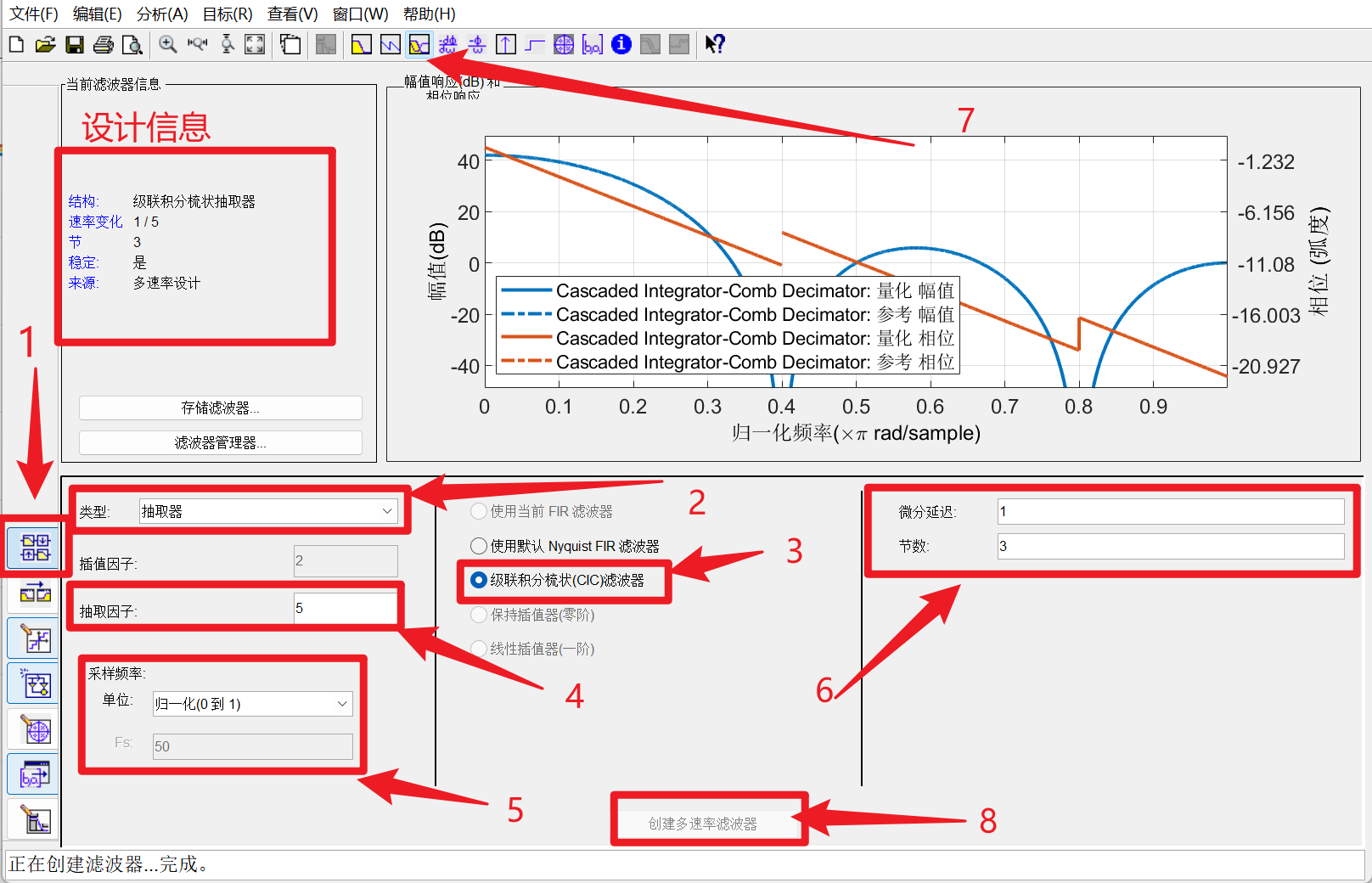
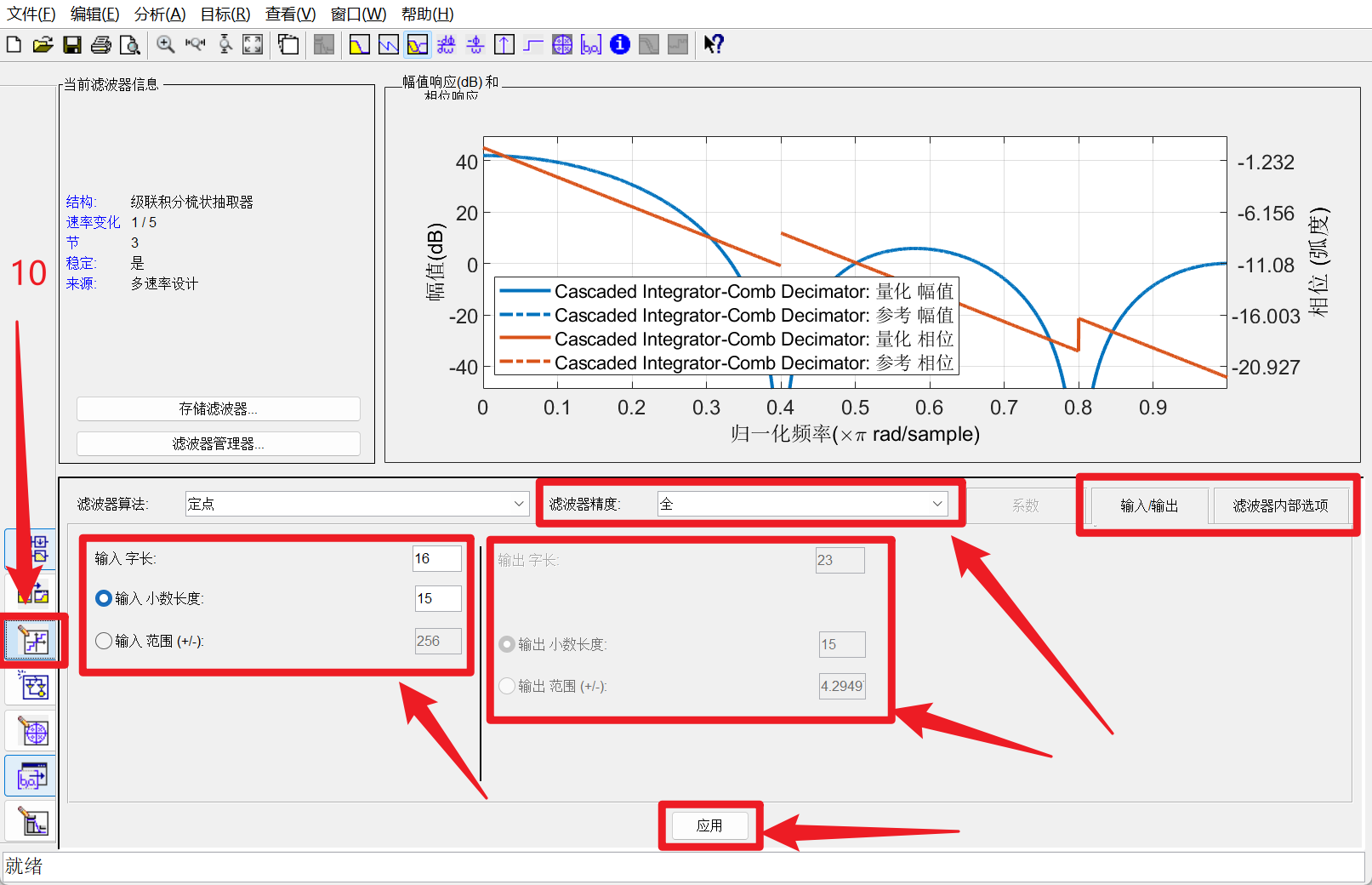
设计完成后,可以选择将滤波器导出为matlab函数经行调用使用,也可以选择直接导出HDL代码经行硬件仿真验证.
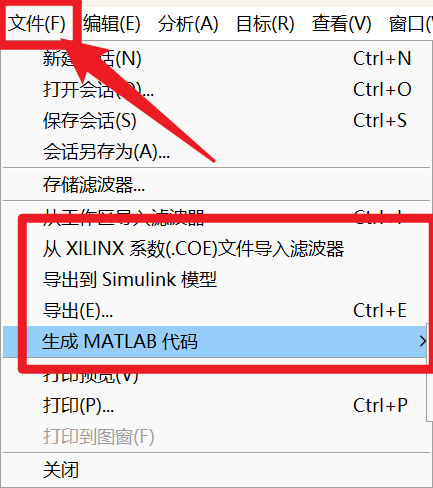
3. matlab 调用函数仿真
通过上述设计过程,已经得到了所使用的滤波器。下面进行滤波器效果仿真测试。
生成一段 \(60 \ \text{Hz} + 270 \ \text{Hz} + 3200 \ \text{Hz}\) 采样率为 \(50 \ \text{kSPS}\) 的混合正弦波信号;
可以通过连续使用两次上述设计的5倍降采样率的CIC滤波器,也可以使用一次25倍降采样率的CIC滤波器实现 \(50 \ \text{kSPS} -> 2 \ \text{kSPS}\) 降采样过程。
函数调用示例:
%%
Fs = 50e3; % sample rate
R = 5; % decimator factor
D = 1; % differential delay
T = 5;
t_50k = 1/Fs * (0:Fs*T-1)';
t_10k = 1/(Fs/R) * (0:(Fs/R)*T-1)';
t_2k = 1/(Fs/R/R) * (0:(Fs/R/R)*T-1)';
f1 = 60; f2 = 270; f3 = 3200;
% Aliasingf = (1 - (f3/(Fs/R/2) - floor(f3/(Fs/2/R))))*(Fs/R/2);
% signals generate
s1 = sin(2*pi*f1*t_50k) + sin(2*pi*f2*t_50k) + sin(2*pi*f3*t_50k);
% filte
y = untitled(s1)/5^5; % 使用5倍降采样率CIC滤波器对信号是s1 进行滤波降采样,5倍降采样,50kSPS -> 10kSPS
y2k = untitled25(s1)/25^5; % 使用25倍降采样率CIC滤波器对信号是s1 进行滤波降采样,25倍降采样,50kSPS -> 2kSPS
yy = untitledHm(y); % 对5倍降采样后的信号y 进行补偿滤波
y1 = untitledf2(y)/5^5; % 使用5倍降采样率CIC滤波器对信号是y 进行滤波降采样,5倍降采样,10kSPS -> 2kSPS
yy1 = untitledf2(yy); % 对5倍降采样后进行补偿滤波的信号yy 继续进行5倍降采样,10kSPS -> 2kSPS
% fft : amplitude
m_s1 = 20*log10(abs(fft(s1)));
m_y = 20*log10(abs(fft(double(y)))); %m_y = m_y - max((m_y));
m_y2k = 20*log10(abs(fft(double(y2k))));
m_yy = 20*log10(abs(fft(double(yy))));
m_y1 = 20*log10(abs(fft(double(y1)))); %m_y1 = m_y1 - max((m_y1));
m_yy1 = 20*log10(abs(fft(double(yy1))));
%
figure
subplot(3,4,[1 2]) % 原始信号s1 时域
plot(t_50k,s1,'-*'); grid; xlim([0,0.05]);
legend([num2str(f1),'Hz + ',num2str(f2),'Hz + ',num2str(f3),'Hz'])
subplot(3,4,[3 4]) % 原始信号s1 幅度谱
x_f=[0:(Fs/length(m_s1)):Fs/2]';
semilogx(x_f,m_s1(1:length(x_f))); grid; xlim([min(x_f) max(x_f)]);
legend([num2str(f1),'Hz + ',num2str(f2),'Hz + ',num2str(f3),'Hz'])
subplot(3,4,5) % 5倍降采样后信号y 时域
plot(t_10k,double(y),'-*'); grid; xlim([0,0.05]);
% legend([num2str(f1),'Hz + ',num2str(f2),'Hz + ',num2str(f3),'Hz','down 5'])
subplot(3,4,6) % 5倍降采样后信号y 幅度谱
x_f=[0:(Fs/R/length(m_y)):Fs/R/2]';
semilogx(x_f,m_y(1:length(x_f))); grid; xlim([min(x_f) max(x_f)]);
% legend([num2str(f1),'Hz + ',num2str(f2),'Hz + ',num2str(f3),'Hz','down 5'])
subplot(3,4,7) % 5倍降采样后级联补偿滤波器信号yy 时域
plot(t_10k,(yy),'-*'); grid; xlim([0,0.05]);
% legend([num2str(f1),'Hz + ',num2str(f2),'Hz + ',num2str(f3),'Hz','down 5 and'])
subplot(3,4,8) % 5倍降采样后级联补偿滤波器信号yy 幅度谱
x_f=[0:(Fs/R/length(m_yy)):Fs/R/2]';
semilogx(x_f,m_yy(1:length(x_f))); grid; xlim([min(x_f) max(x_f)]);
subplot(3,4,9) % 5倍降采样信号y再5倍降采样的信号y1 时域
plot(t_2k,double(y1),'-*'); grid; xlim([0,0.05]);
subplot(3,4,10) % 5倍降采样信号y再5倍降采样的信号y1 幅度谱
x_f=[0:(Fs/R/R/length(m_y1)):Fs/R/R/2]';
semilogx(x_f,m_y1(1:length(x_f))); grid; xlim([min(x_f) max(x_f)]);
subplot(3,4,11) % 5倍降采样后级联补偿滤波器信号yy再5倍降采样的信号yy1 时域
plot(t_2k,double(yy1),'-*'); grid; xlim([0,0.05]);
subplot(3,4,12) % 5倍降采样后级联补偿滤波器信号yy再5倍降采样的信号yy1 幅度谱
x_f=[0:(Fs/R/R/length(m_yy1)):Fs/R/R/2]';
semilogx(x_f,m_yy1(1:length(x_f))); grid; xlim([min(x_f) max(x_f)]);
%
figure
subplot(3,4,[1 2]) % 原始信号s1 时域
plot(t_50k,s1,'-*'); grid; xlim([0,0.05]);
subplot(3,4,[3 4]) % 原始信号s1 幅度谱
x_f=[0:(Fs/length(m_s1)):Fs/2]';
semilogx(x_f,m_s1(1:length(x_f))); grid; xlim([min(x_f) max(x_f)]);
subplot(3,4,[5 6]) % 25倍降采样后信号y2k 时域
plot(t_2k,double(y2k),'-*'); grid; xlim([0,0.05]);
subplot(3,4,[7 8]) % 25倍降采样后信号y2k 幅度谱
x_f=[0:(Fs/R/R/length(m_y2k)):Fs/R/R/2]';
semilogx(x_f,m_y2k(1:length(x_f))); grid; xlim([min(x_f) max(x_f)]);
subplot(3,4,[9 10]) % 5倍降采样信号y再5倍降采样的信号y1 时域
plot(t_2k,double(y1),'-*'); grid; xlim([0,0.05]);
subplot(3,4,[11 12]) % 5倍降采样信号y再5倍降采样的信号y1 幅度谱
x_f=[0:(Fs/R/R/length(m_y1)):Fs/R/R/2]';
semilogx(x_f,m_y1(1:length(x_f))); grid; xlim([min(x_f) max(x_f)]);
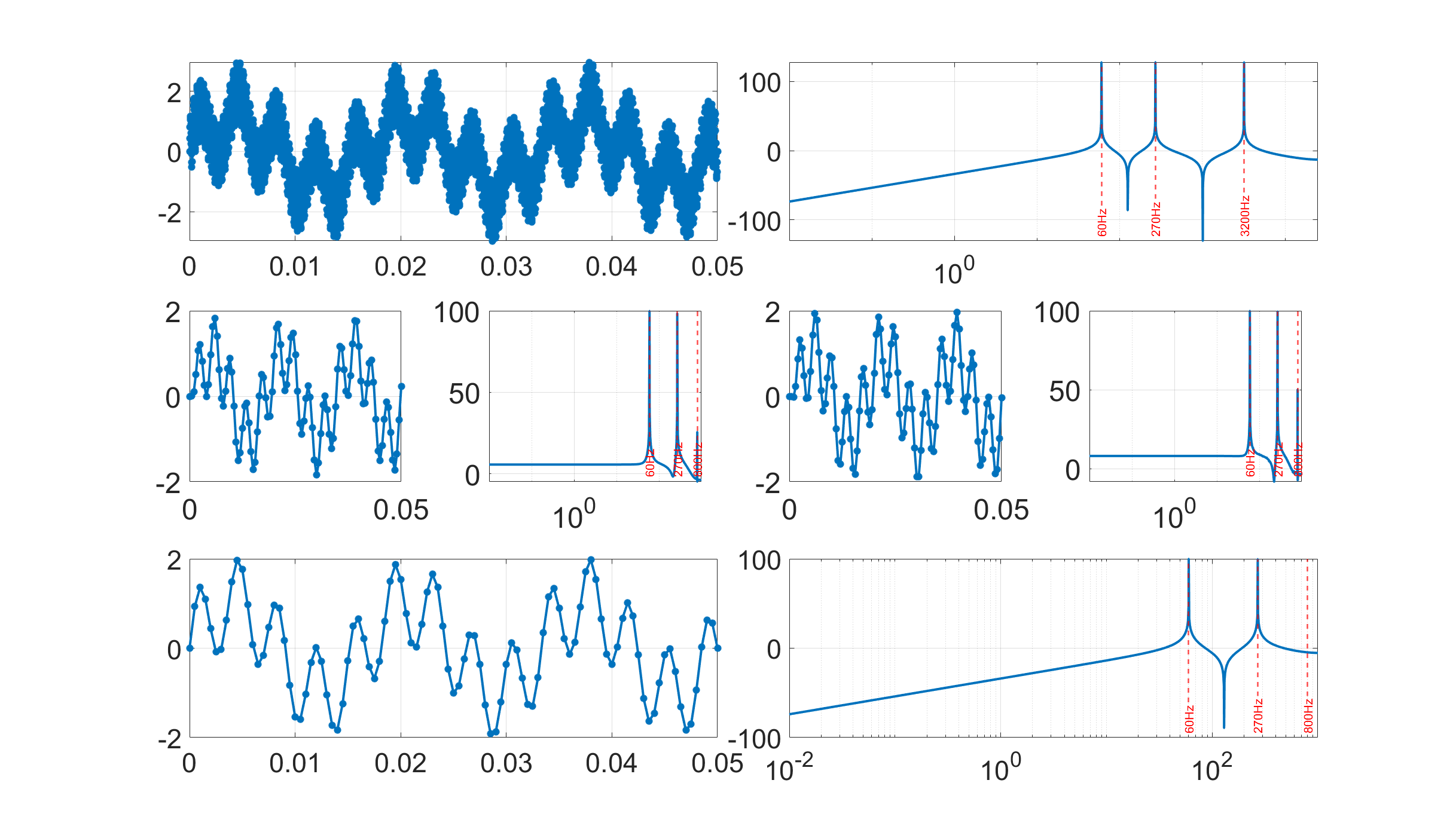
最终效果图:
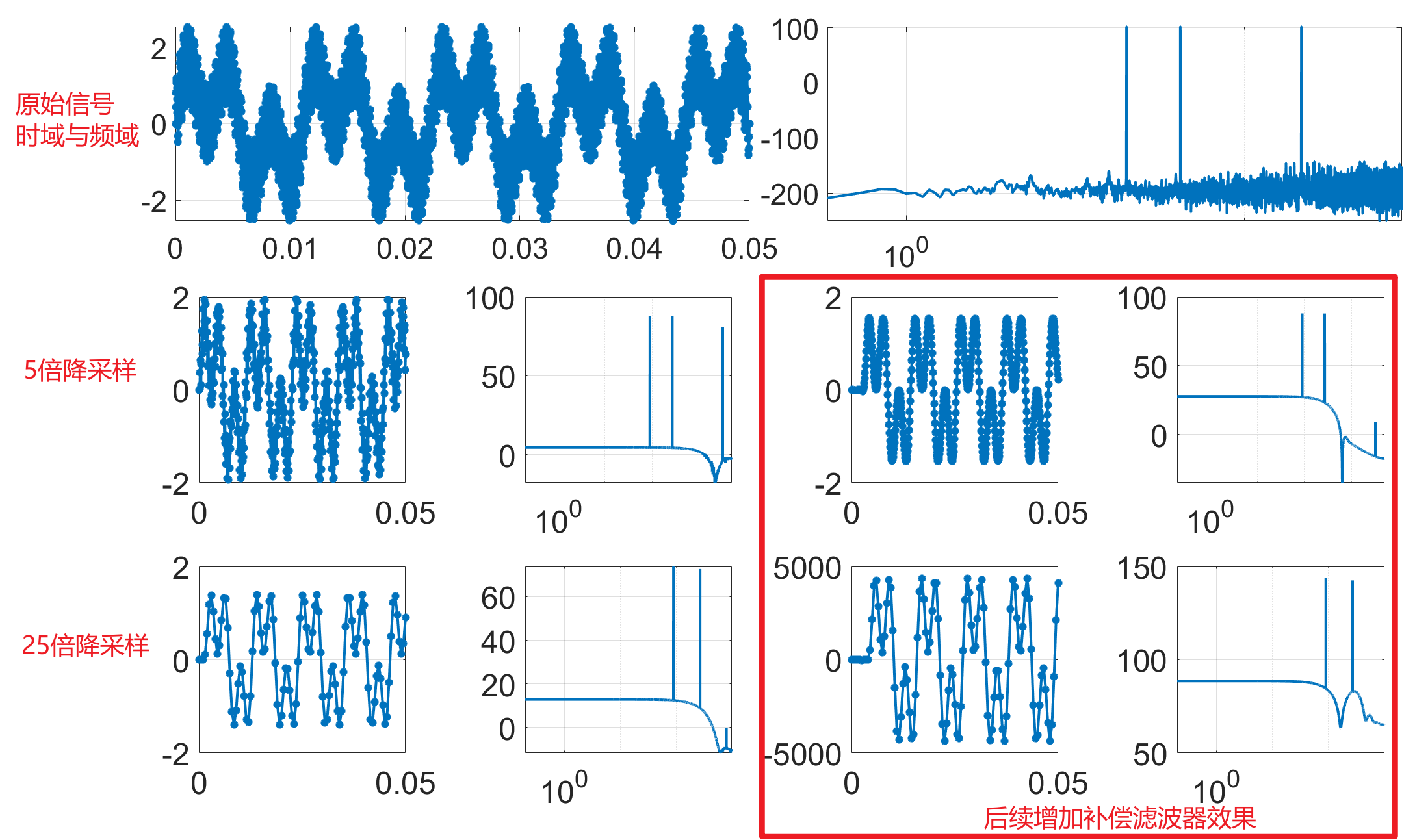
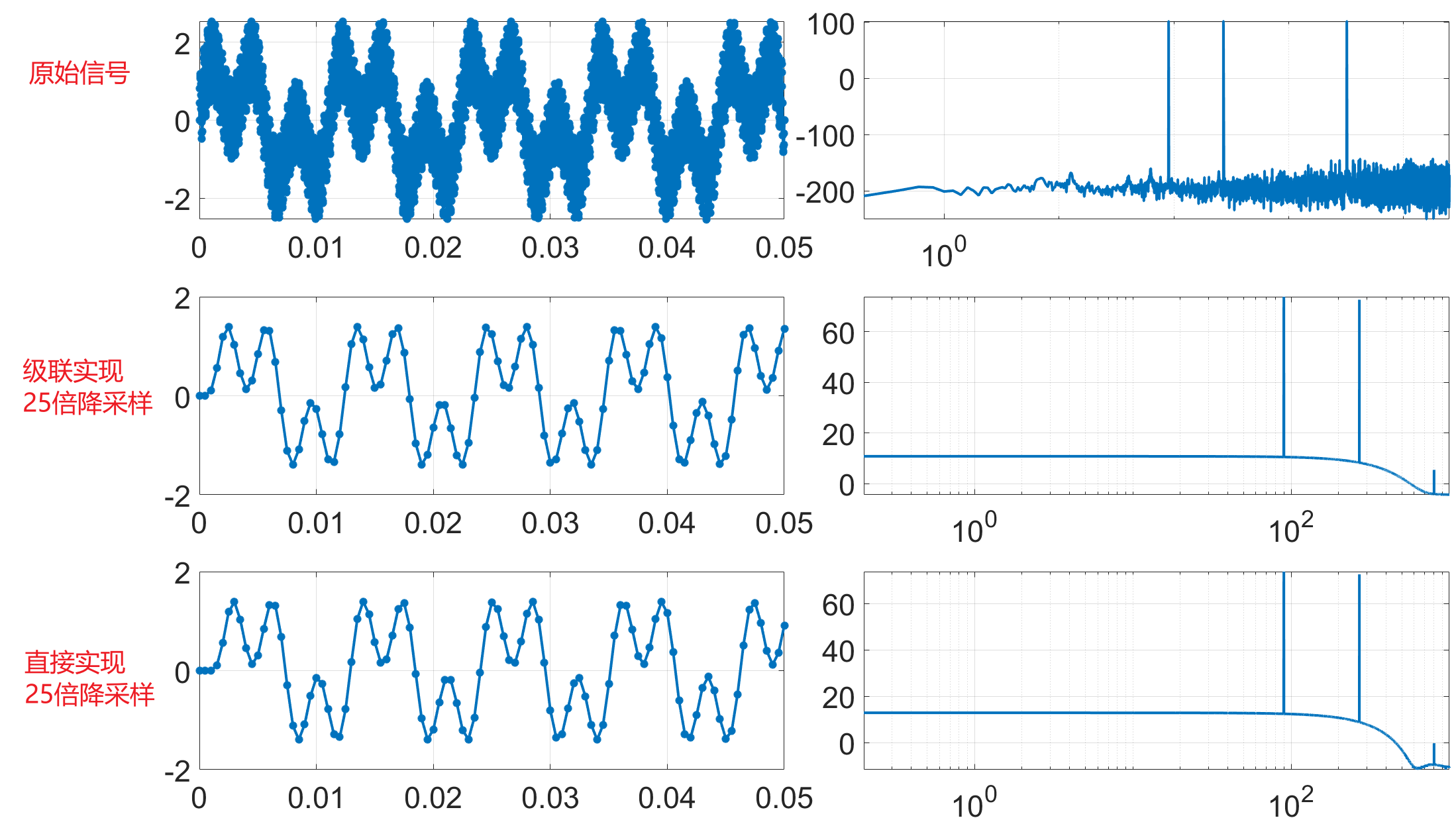
在上述仿真结果中可以看到,当前滤波器参数设计情况加,发生了滤波后高频混叠显现,尤其是在未使用补偿滤波器情况下尤为严重。
这说明,在经行CIC滤波器设计的时候要考虑滤波效果和级联补偿滤波器的作用。
4. simulink 进行仿真
前面在说到可以从filterDesigner工具箱中导出以供使用的滤波器,其中一项为可以直接导出为simulink模型,可以导出为使用CIC滤波器模块的模型,也可以是使用基本模块组合成的CIC滤波器。
使用CIC滤波器模块的模型
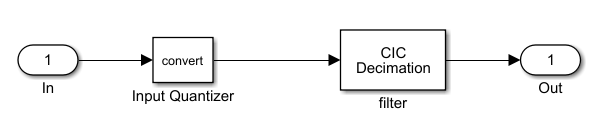
使用基本模块组成的CIC滤波器模型

仿真模型如下
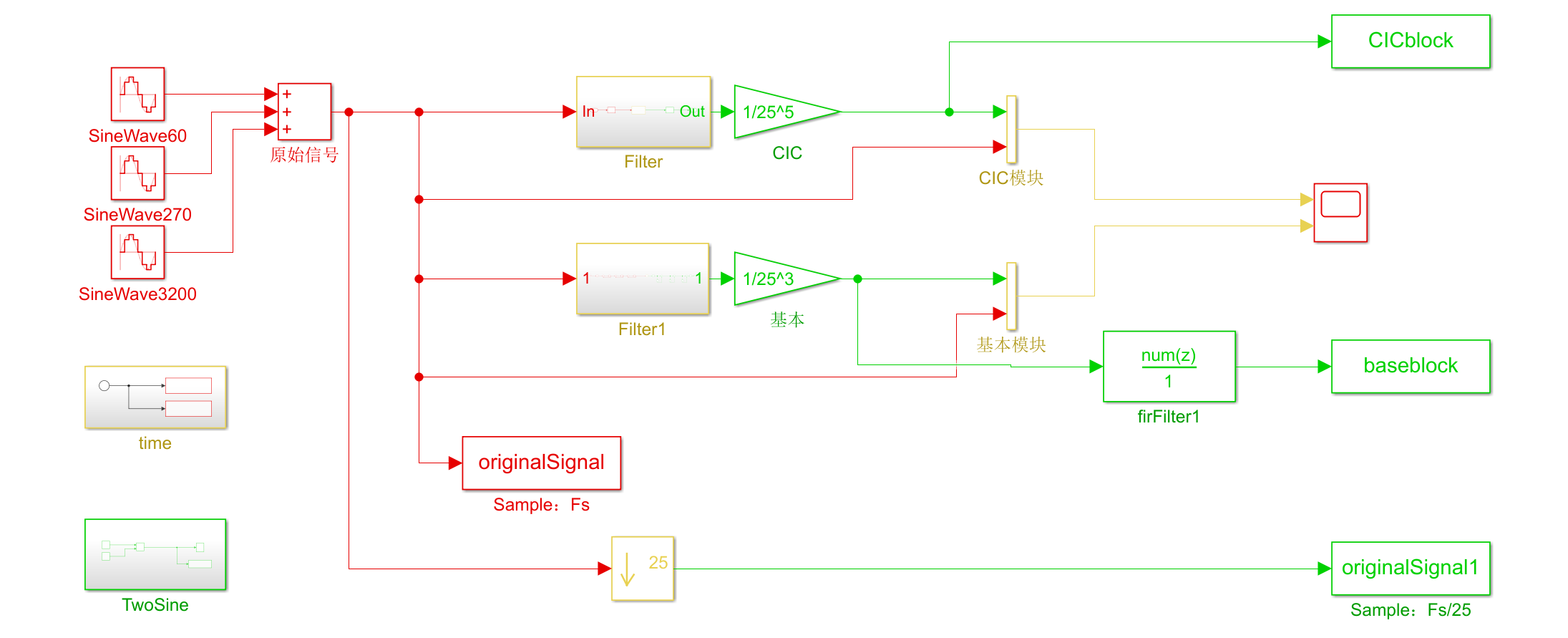
设置一个输入,观察效果
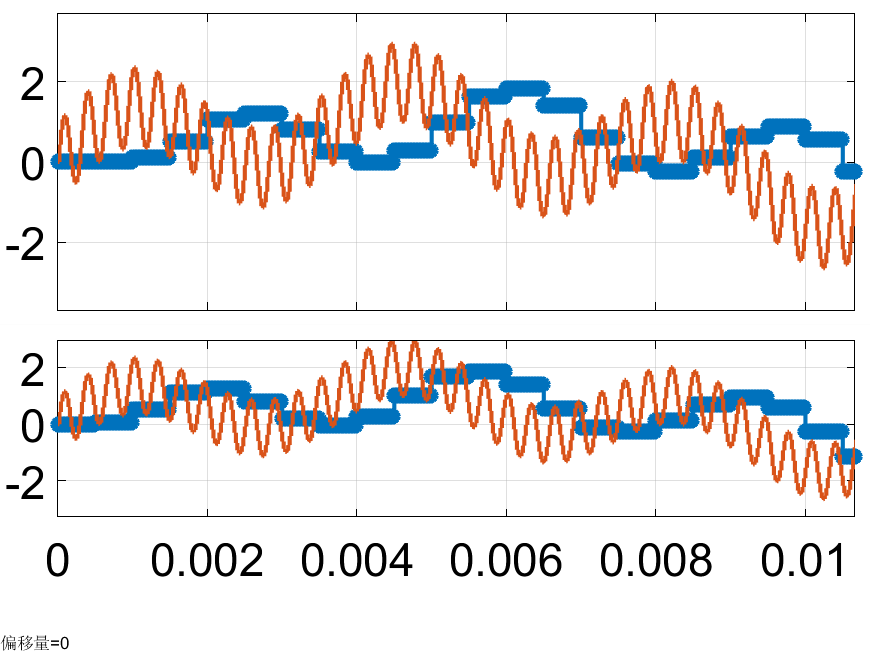
60+270+3200


 浙公网安备 33010602011771号
浙公网安备 33010602011771号