概率密度估计(EM算法,混合朴素贝叶斯模型(朴素贝叶斯模型的无监督学习),因子模型)
概率密度估计最基本任务是为了估计在给定X下,会产生类似于X的输入的概率。
一般的估计方法:
1、柱状图估计:
$P(X) = \frac{1}{N}*\frac{N(x)}{V} $
这里,$ \frac{1}{N}$是归一化参数,$\frac{N(x)}{V} $表示数据的密度,V是超立方体,是设计好的一个常数,最好的估计下,V->0,NV趋于无穷。
通常情况下可以选择$V=1/\sqrt{N}$
2、最近邻估计:
3、Parzen windows:径向函数估计:
其中径向函数估计有有参数和无参数的方法(类似于算法当中,KNN的RBF和linear model中的RBF估计(RBF网络)):
GMM就是Parzen窗的密度估计的有参数模型:
由于GMM最后需要最大化似然概率,但是相加的概率无法直接用梯度法求解,由此引出EM算法(为了计算最大似然概率得出)
EM算法
完整的数据是(X,J),但是J未知,所以不完整数据(X)
求完整数据的联合概率$\mathbb{P}[x_{n},j_{n}|\Theta]$,利用贝叶斯公式:
$$ \begin{align} \mathbb{P}[x_{n},j_{n}|\Theta] & =\mathbb{P}[j_{n}|\Theta]\mathbb{P}[x_{n}|j_{n},\Theta] \\&=w_{j_{n}}P_{j_{n}}(x_{n};\theta_{j_{n}}) \\\end{align}$$
因为data是相互独立的,所以:
$$ \begin{align} \mathit{P}(\mathit{X,J}|\Theta) &=\prod_{n=1}^N\mathbb{P}[x_{n},j_{n}|\Theta] \\&=\prod_{n=1}^Nw_{j_{n}}P_{j_{n}}(x_{n};\theta_{j_{n}}) \\\end{align}$$
令$N_{k}$是在$J$中$k$出现的次数,在$k$中出现的数据点由$X_{k}$表示,也就是说$X_{k} = { x_n \in X; j_n \in k}$。所以整个完全数据$(X,J)$的最大似然的对数值(log-liklihood)如下所示:
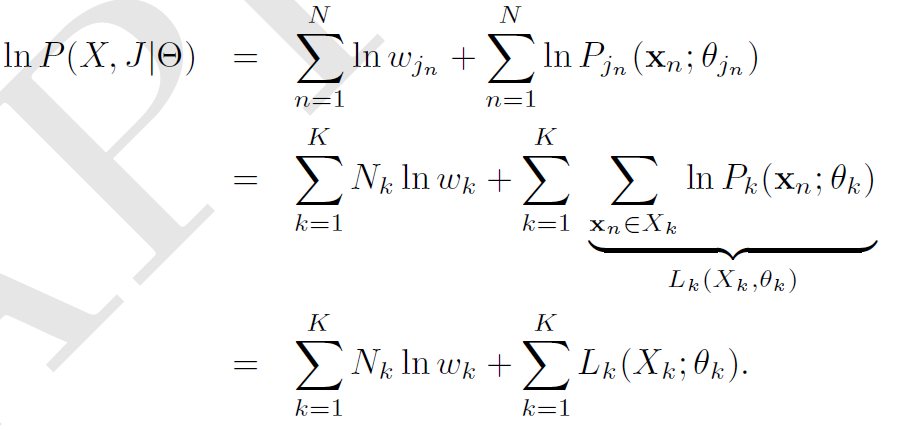
EM 算法通过从一个错误的参数猜测开始,通过数据信息和错误的模型信息来得到一个更好的模型,最后得到一个能够解释这个数据的模型。EM算法在强化学习当中也由一席之地。
EM算法推导






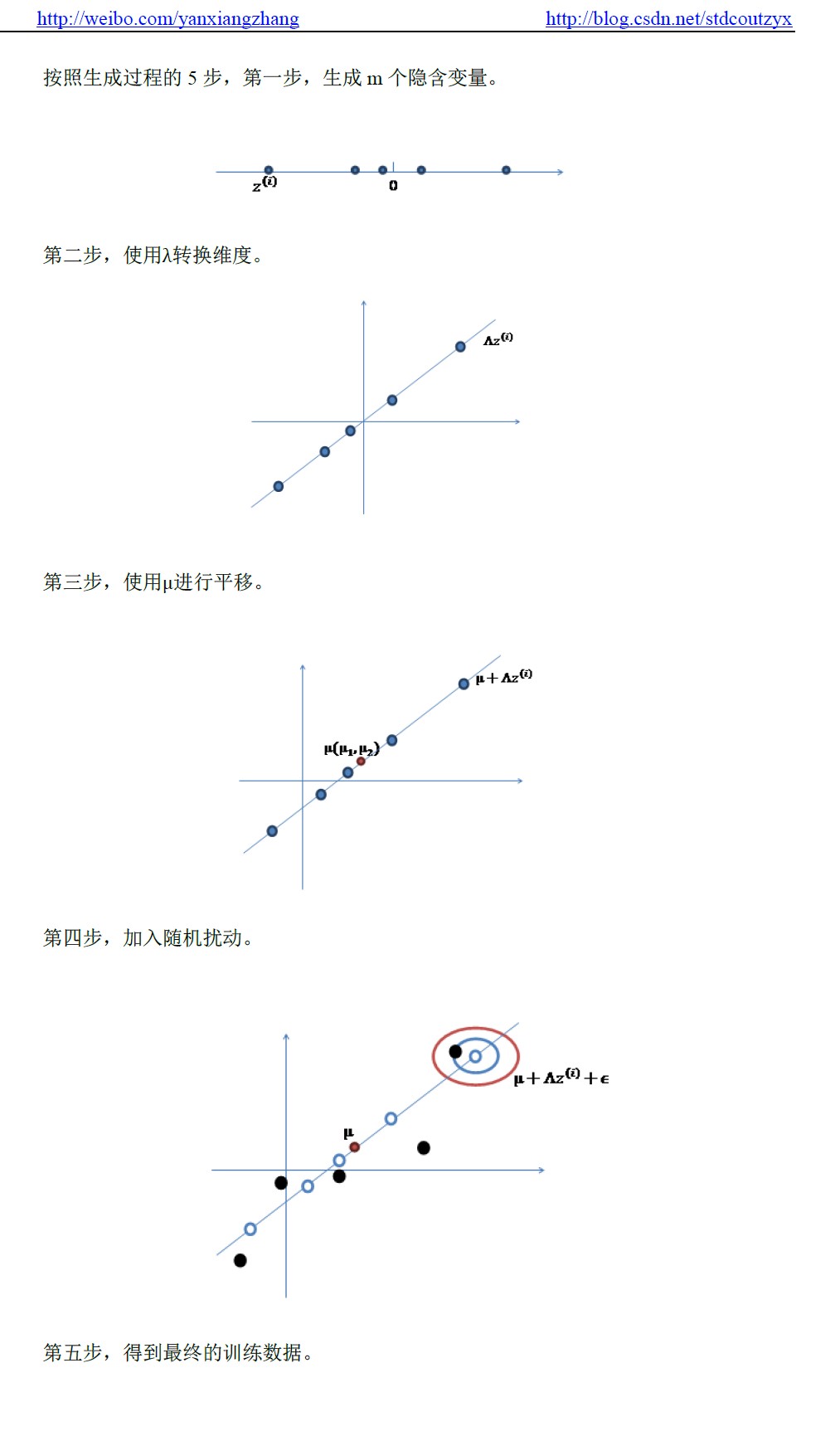
因子模型
来源:https://blog.csdn.net/stdcoutzyx/article/details/37559995








 浙公网安备 33010602011771号
浙公网安备 33010602011771号