笔记06. 假设检验

设检验中的几个核心概念：否定域（拒绝域）、显著性水平 α、p 值（p-value）**。这些概念在统计推断中彼此紧密相关，理解它们能帮助你正确设计统计检验并解读检验结果。

---

📖 第一人称心路独白：关于 H₀、5%，以及那条我必须画出的界线

有时候，我觉得做假设检验就像是在和“未知”对话。

我面前摆着一份假设书，标题写着：
“H₀：事情就是这样的。”

我不知道这个假设是不是对的，但在没有更充足的证据前，我愿意把它当成一个起点，一个暂时不会轻易推翻的立场。

可我心里总是有一点不安。
我会偷偷问自己：

“如果它明明是真的，我却误以为它是错的怎么办？”
“我会不会冤枉了一个其实清白的假设？”

这种担忧并不是杞人忧天，而是统计学里再正常不过的事情——
它有个名字，叫第一类错误。

我不想轻易犯这种错误。
我希望自己稳一点、慎重一点。
所以我给自己设下了一条界限：

“让我犯这种错的概率不要超过 5%。”

也就是说，如果未来我的判断真的错了，那至少我知道——
这是我事先同意的风险上限，是我愿意承担、能解释给自己听的范围。

于是，我开始翻看数据，把样本交给统计量，让它去告诉我它所看到的世界。
我让自己安静下来，跟着它的分布慢慢描绘那条界线。

根据这条分布，我画出一片地方。
它像是一块红色的禁区，或者说是一个我心里暗暗标出的**“危险地带”**：

只要统计量落到这里，就说明这种结果太罕见了，罕见到如果 H₀ 真的为真，那我几乎不会看到它。

这片区域，就是统计学里的拒绝域。
但对我来说，它更像是我设给自己的一个提醒：

“如果你走到这里，就代表你真的有理由怀疑 H₀。”

于是，当我真正拿到一个统计量值时，我会看着那条红线，问自己：

“它有没有越界？是不是进入了我不想随便踏入的那片区域？”

如果它真的跨过去了，我便会拒绝 H₀，哪怕心里仍然知道：

“我这样做有 5% 的可能是在误会一个真实的假设。”

但那 5%，是我自己定下、自己承担、自己愿意面对的。

这一刻，我并不是在追求绝对的真相，而是在有限的信息下，做出一个最稳妥、最可控、最合乎理性的决定。

---

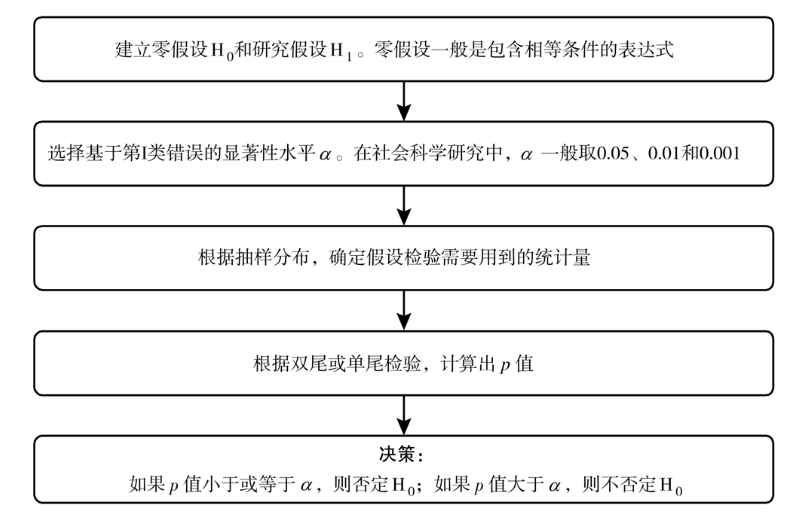
📌 1. 假设检验的整体框架（快速回顾）

假设检验的目标是：
根据样本数据判断总体是否具有某个特征。核心是比较数据支持原假设 H₀ 的程度。

● 原假设 H₀（null hypothesis）：我们要检验的基准假设（例如平均值 = μ₀）。
● 备择假设 H₁（alternative hypothesis）：与原假设对立的假设（例如平均值 ≠ μ₀）。

检验的逻辑是：

如果样本数据与 H₀ 假设“太不一致”，则拒绝 H₀。

---

📌 2. 否定域（拒绝域 Rejection Region）

✔ 定义

否定域也叫“拒绝域”，指的是在某个显著性水平下，会导致我们拒绝原假设 H₀ 的统计量取值区域。

例如：

• 做均值的 z 检验
• 设显著性水平 α = 0.05
• 双侧检验下的临界值为 ±1.96

则当统计量 Z 超过这个范围（比如 Z > 1.96 或 Z < -1.96）时，我们认为样本与 H₀ 差异太大，进入“否定域”，从而拒绝 H₀。

✔ 直观理解

否定域 = “如果统计量落在这里，就是太极端太反常了，说明 H₀ 可能不成立”。

---

📌 3. 显著性水平 α（Significance Level）

✔ 定义

显著性水平 α 是你愿意承担的错误拒绝 H₀ 的最大概率。
也就是说：

α = 在 H₀ 为真时你仍然拒绝 H₀ 的概率（即第一类错误概率）。

常见取值：

• α = 0.05（最常用）
• α = 0.01（更严格）
• α = 0.1（较宽松）

✔ α 的作用

1. 决定拒绝域的大小
   α 越小 → 拒绝域越窄 → 需要更极端的证据才能拒绝 H₀。

2. 控制错误判断的风险
   α 是事先确定的（不能看数据之后再改）。

---

📌 4. p 值（p-value）

✔ 定义

p 值是：

在原假设 H₀ 为真的前提下，得到当前样本结果或更极端结果的概率。

它衡量的是观察到的数据对反对 H₀ 的支持程度。

✔ p 值大小的含义：

• 小 p 值 → 数据非常不支持 H₀ → 倾向拒绝 H₀
• 大 p 值 → 数据与 H₀ 可以“和平共处” → 没有证据拒绝 H₀

常用判断规则：

• 如果 p < α → 拒绝 H₀
• 如果 p ≥ α → 没有足够证据拒绝 H₀（注意不是接受 H₀）

✔ 直觉理解

你可以把 p 值看成：

“如果 H₀ 是真的，我见到这么极端的数据会有多罕见？”

越罕见，说明 H₀ 越可疑。

---

📌 5. 三者之间的关系（重点）

概念	谁决定？	作用	本质含义
显著性水平 α	你事先设定	决定拒绝域	你希望控制的第一类错误概率
否定域（拒绝域）	由 α 决定	检验统计量落入此区 → 拒绝 H₀	“太极端”的范围
p 值	由数据算出	与 α 比较决定是否拒绝 H₀	数据反对 H₀ 的强度指标

关系总结一句话：

α 决定拒绝域；数据给你 p 值；比较 p 与 α 决定是否拒绝 H₀。

---

📌 6. 一个直观例子（最易懂）

假设你想检验产品重量是否仍为 500g。

设定：

• H₀：平均重量 = 500g
• H₁：平均重量 ≠ 500g
• 显著性水平 α = 0.05

计算：

• 得到检验统计量 Z = 2.3
• 查表可得 p = 0.021

判断：

• 因为 p = 0.021 < 0.05
  → 落入拒绝域
  → 拒绝 H₀

结论：产品平均重量很可能不再是 500g。