笔记02. 卡方分布

《回归分布》第二章
误差平方和是统计学、机器学习、工程优化等领域的 “底层工具”，它的有效性和普适性，源于几个核心优势 ——不抵消偏差、放大关键异常、数学性质优良。比如机器学习里的均方误差（MSE），本质就是 “平均化的误差平方和”，是最常用的回归任务损失函数之一 —— 它的优化目标，就是最小化预测值和真实值的误差平方和。

卡方分布的核心本质是 “独立标准正态误差的平方和”，这一定义决定了它天然适配各类需要量化“偏差累积效应”的实际问题。

深入浅出卡方分布：定义、与样本方差的关联及核心应用

在统计学的大家族中，卡方分布（\(\chi^2\)分布）是一类基于正态分布衍生的连续型概率分布，它在方差检验、拟合优度分析、独立性检验等场景中扮演着不可替代的角色。本文将抛开复杂的衍生分布（如F分布），聚焦卡方分布的核心定义、与样本方差的深层关联、直观性质及典型应用，帮助读者构建清晰的知识框架。

一、 卡方分布的核心定义

卡方分布的定义完全基于标准正态分布的平方和，这是理解它的根本出发点。

1. 数学定义

若随机变量 \(Z_1,Z_2,\dots,Z_n\) 相互独立，且均服从标准正态分布，即 \(Z_i \sim N(0,1)\)，则它们的平方和所构成的新随机变量 \(\chi^2\) 服从自由度为 \(n\) 的卡方分布，记为：

\[\chi^2 = \sum_{i=1}^n Z_i^2 \sim \chi^2(n) \]

2. 关键概念：自由度

这里的自由度 \(n\) 指的是参与平方和计算的独立标准正态变量的个数。自由度是卡方分布的核心参数，它直接决定了分布的形状。

二、 样本方差与卡方分布的紧密关联

卡方分布最核心的应用场景之一，就是研究样本方差与总体方差的关系。这也是它在方差检验中发挥作用的理论基础。

1. 关键定理：正态总体下的样本方差分布

设总体 \(X\) 服从正态分布 \(N(\mu,\sigma^2)\)，其中 \(\mu\) 是总体均值，\(\sigma^2\) 是总体方差；从该总体中抽取容量为 \(n\) 的简单随机样本 \(X_1,X_2,\dots,X_n\)，样本均值为 \(\bar{X} = \frac{1}{n}\sum_{i=1}^n X_i\)，样本方差为：

\[S^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i-\bar{X})^2 \]

则有如下重要结论：

\[\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1) \]

2. 自由度为什么是 \(n-1\)？

这个结论中自由度为 \(n-1\) 而非 \(n\)，是统计学中典型的自由度损失现象：

• 样本方差的计算依赖样本均值 \(\bar{X}\)；
• 样本均值 \(\bar{X}\) 是一个约束条件（\(\sum_{i=1}^n (X_i-\bar{X})=0\)），这意味着 \(n\) 个偏差 \((X_i-\bar{X})\) 中只有 \(n-1\) 个是独立的；
• 因此，最终服从的卡方分布自由度为 \(n-1\)。

3. 实战例子：检验零件尺寸方差是否达标

某工厂声称生产的零件尺寸方差 \(\sigma^2=0.04\)（方差越小，精度越高）。为验证该说法，质检人员抽取了 \(n=10\) 个零件作为样本，计算得样本方差 \(S^2=0.06\)。

我们可以利用卡方分布进行分析：

1. 计算检验统计量：
   \[\frac{(n-1)S^2}{\sigma^2} = \frac{9\times0.06}{0.04}=13.5 \]

2. 该统计量服从 \(\chi^2(9)\) 分布，查阅卡方分布表可知，\(\chi^2_{0.90}(9)=14.684\)；
3. 由于 \(13.5 < 14.684\)，在 \(0.10\) 的显著性水平下，没有足够证据否定工厂的说法，即认为零件尺寸方差符合标准。

三、 卡方分布的均值与方差：直观理解 \(n\) 和 \(2n\)

对于服从 \(\chi^2(n)\) 分布的随机变量，其均值和方差具有简洁的形式：

• 均值：\(E[\chi^2(n)] = n\)
• 方差：\(D[\chi^2(n)] = 2n\)

直观推导（非严格证明）

我们可以从卡方分布的定义出发，用标准正态分布的性质直观理解：

1. 均值的推导
   对于标准正态变量 \(Z_i \sim N(0,1)\)，根据方差的定义：

   \[D[Z_i] = E[Z_i^2] - (E[Z_i])^2 \]

   由于 \(E[Z_i]=0\)，\(D[Z_i]=1\)，因此 \(E[Z_i^2]=1\)。
   而 \(\chi^2 = \sum_{i=1}^n Z_i^2\)，根据期望的可加性：

   \[E[\chi^2] = \sum_{i=1}^n E[Z_i^2] = n \times 1 = n \]

2. 方差的推导
   标准正态变量的四阶矩 \(E[Z_i^4]=3\)（这是标准正态分布的固有性质），因此 \(Z_i^2\) 的方差为：

   \[D[Z_i^2] = E[Z_i^4] - (E[Z_i^2])^2 = 3-1=2 \]

   由于 \(Z_1,Z_2,\dots,Z_n\) 相互独立，方差也具有可加性：

   \[D[\chi^2] = \sum_{i=1}^n D[Z_i^2] = n \times 2 = 2n \]

简单来说：每个独立的 \(Z_i^2\) 贡献1个单位的均值和2个单位的方差，\(n\) 个变量相加，均值就是 \(n\)，方差就是 \(2n\)。

四、 卡方分布不对称性的本质原因

卡方分布的概率密度函数（PDF）是右偏分布，即峰值偏左，右侧有一条长长的“尾巴”。这种不对称性可以从两个角度直观理解：

1. 取值范围的约束

卡方分布的随机变量是标准正态变量的平方和，而平方数的取值范围是 \([0,+\infty)\)，即卡方变量的取值不可能为负数。

• 分布的左侧被“截断”在0处，无法向左延伸；
• 右侧则可以随着平方和的增大无限延伸；
• 这种取值范围的非对称性，直接导致了分布的右偏。

2. 自由度对偏度的影响

• 当自由度 \(n\) 较小时（如 \(n=1,2\)），右偏程度非常明显；
• 随着自由度 \(n\) 的增大，卡方分布的峰值逐渐右移，偏度逐渐减小，越来越接近对称的正态分布（这是中心极限定理的体现）。

五、 总结卡方分布

卡方分布是统计学中连接正态分布与样本方差的桥梁，其核心知识点可归纳为：

1. 定义：\(n\) 个独立标准正态变量的平方和，自由度 \(n\) 决定分布形状；
2. 与样本方差的关系：正态总体下 \(\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)\)，是方差检验的理论基础；
3. 核心应用：样本方差的检验与区间估计、拟合优度检验、独立性检验；
4. 关键性质：均值为 \(n\)，方差为 \(2n\)；取值非负导致右偏分布，自由度越大越接近正态。

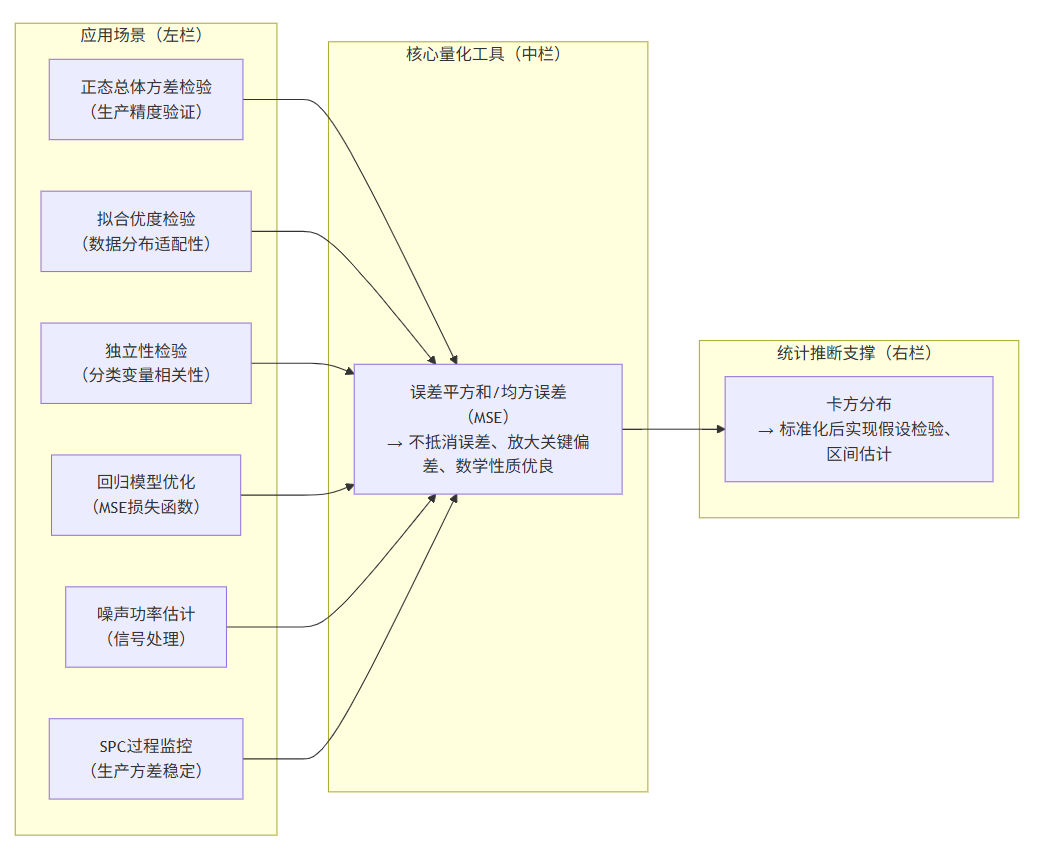
卡方分布的实战应用场景：平方和构造的合理性与分布必然性

卡方分布的核心本质是 “独立标准正态误差的平方和”，这一定义决定了它天然适配各类需要量化“偏差累积效应”的实际问题。我们先梳理基于平方和的核心应用场景，再从问题需求和数学本质两层，解释“为什么平方和是合理选择”以及“为什么这类平方和恰好服从卡方分布”。

一、 卡方分布的核心应用场景（基于独立误差平方和）

所有场景的共性是：需要衡量一组独立偏差的总大小，且偏差本身服从（或可标准化为）正态分布。以下是5类典型落地场景：

1. 正态总体方差的检验与区间估计（最基础场景）

• 核心问题：工厂零件尺寸、仪器测量值等数据通常服从正态分布，我们需要判断“样本方差是否与总体方差一致”（比如验证生产精度是否达标）。
• 平方和的构造逻辑：样本方差的本质是“样本值与样本均值的误差平方和”，即 \(\sum_{i=1}^n(X_i-\bar{X})^2\)。为了消除量纲影响并满足卡方分布的前提，我们将其标准化为 \(\frac{(n-1)S^2}{\sigma^2} = \frac{\sum_{i=1}^n(X_i-\bar{X})^2}{\sigma^2}\)。
• 为什么用卡方分布：当总体服从 \(N(\mu,\sigma^2)\) 时，误差 \(\frac{X_i-\bar{X}}{\sigma}\) 可标准化为近似独立的正态变量，其平方和恰好服从 \(\chi^2(n-1)\) 分布。

2. 拟合优度检验：验证数据是否符合理论分布

• 核心问题：判断观测数据是否服从某一理论分布（比如骰子是否均匀、用户性别分布是否符合预期比例）。
• 平方和的构造逻辑：定义“观测频数与理论频数的偏差” \(O_i-E_i\)，构造统计量 \(\chi^2=\sum_{i=1}^k\frac{(O_i-E_i)^2}{E_i}\)。这里的平方是为了保留偏差方向，分母 \(E_i\) 是为了消除组容量差异的影响。
• 为什么用卡方分布：当样本量足够大时，偏差 \(\frac{O_i-E_i}{\sqrt{E_i}}\) 近似服从独立标准正态分布，因此其平方和近似服从自由度为 \(k-r-1\) 的卡方分布（\(r\) 是待估参数个数）。

3. 列联表独立性检验：判断两个分类变量是否相关

• 核心问题：分析两个分类变量是否独立（比如“用户年龄段”与“购买偏好”是否相关、“吸烟与否”与“患肺癌”是否相关）。
• 平方和的构造逻辑：基于列联表，计算每个单元格的“观测频数 \(O_{ij}\)”与“独立假设下的期望频数 \(E_{ij}\)”，构造统计量 \(\chi^2=\sum_{i=1}^r\sum_{j=1}^c\frac{(O_{ij}-E_{ij})^2}{E_{ij}}\)。
• 为什么用卡方分布：独立假设下，偏差 \(\frac{O_{ij}-E_{ij}}{\sqrt{E_{ij}}}\) 近似独立标准正态分布，平方和服从自由度为 \((r-1)(c-1)\) 的卡方分布。

4. 信号处理：噪声功率的估计与检测

• 核心问题：通信或雷达系统中，需要估计背景噪声的功率，或检测“是否存在有用信号”。
• 平方和的构造逻辑：噪声信号通常服从正态分布 \(N(0,\sigma^2)\)（均值为0的白噪声），噪声功率的本质是噪声幅值的平方期望。我们取 \(n\) 个独立的噪声采样值 \(Z_1,Z_2,\dots,Z_n\)，构造平方和 \(\sum_{i=1}^n Z_i^2\) 来估计总功率。
• 为什么用卡方分布：噪声采样值 \(Z_i\) 本身就是独立正态变量，标准化后 \(\frac{Z_i}{\sigma}\sim N(0,1)\)，因此 \(\frac{1}{\sigma^2}\sum_{i=1}^n Z_i^2 \sim \chi^2(n)\)，可直接用卡方分布对功率进行区间估计。

5. 质量管理：过程方差的监控（SPC控制图）

• 核心问题：在生产过程中，实时监控产品质量特性的方差是否稳定（比如芯片尺寸的波动是否超出阈值）。
• 平方和的构造逻辑：采用“极差法”或“方差法”监控，其中方差法的核心是计算每个子组的误差平方和 \(\sum_{i=1}^m(X_{ij}-\bar{X}_j)^2\)（\(m\) 是子组容量，\(j\) 是子组序号）。
• 为什么用卡方分布：正态总体下，子组平方和标准化后服从卡方分布，因此可以设定卡方控制图的上下限，判断过程方差是否失控。

二、 为什么构造平方和解决问题更合理？

在上述场景中，我们完全可以用“绝对值和”\(\sum|误差|\) 来衡量偏差累积，但平方和是更优选择，原因有4点：

1. 消除正负误差的相互抵消

误差本身是有正有负的（比如测量值可能高于或低于真实值）。如果直接对误差求和，正负误差会相互抵消，导致总偏差被低估。

• 例子：测量3个物体的误差为 \(+2, -1, -1\)，求和结果为 \(0\)，看似无偏差；但平方和为 \(4+1+1=6\)，能真实反映总偏差大小。
• 平方运算的本质是“保留所有偏差的贡献，不抵消、不遗漏”。

2. 放大关键的大偏差，符合实际需求

在大多数实际问题中，大偏差的危害远大于小偏差的总和（比如生产中尺寸超标的零件、信号中过大的噪声脉冲）。

• 平方运算具有“非线性放大”效应：偏差从 \(1\) 增加到 \(3\)，平方值从 \(1\) 增加到 \(9\)，大偏差的权重被显著提升。
• 这种放大特性，恰好契合了“优先关注极端偏差”的实际需求（比如质检中重点排查不合格品）。

3. 数学性质优良，便于理论推导与计算

平方和的数学可处理性远高于绝对值和：

• 可加性：独立随机变量的平方和，其方差与期望均可直接相加（这是卡方分布均值 \(n\)、方差 \(2n\) 的推导基础）；
• 微分性质：平方函数 \(f(x)=x^2\) 处处可导，方便用微积分工具求最优解（比如最小二乘法的核心就是最小化误差平方和）；
• 与方差的天然关联：方差的定义是 \(D(X)=E[(X-E[X])^2]\)，平方和是方差的样本估计量，二者一脉相承。

4. 与正态分布的完美适配

绝大多数自然现象和工程数据都服从正态分布（中心极限定理保证）。而正态变量的平方和恰好服从卡方分布，这种“分布匹配”是统计学的重要桥梁——如果用绝对值和，很难找到对应的理论分布，无法进行假设检验和区间估计。

三、 为什么这类平方和恰好服从卡方分布？

核心结论：只有当平方和的“构成项是独立标准正态变量”时，其总和才服从卡方分布。这不是偶然，而是由定义和数学推导共同决定的，分两步理解：

1. 卡方分布的定义是“因”，平方和服从分布是“果”

卡方分布的定义就是：若 \(Z_1,Z_2,\dots,Z_n \sim_{i.i.d.} N(0,1)\)，则 \(\chi^2=\sum_{i=1}^n Z_i^2 \sim \chi^2(n)\)。

• 这个定义是人为规定的吗？不是。它是统计学家长期研究后，对“独立标准正态平方和”这一特殊形式的命名与建模。
• 就像“正态分布”描述了“大量独立随机变量的和”的分布规律一样，卡方分布专门描述“独立标准正态变量的平方和”的规律。

2. 实际问题中的平方和，可通过标准化转化为定义形式

在前面的应用场景中，我们构造的平方和并非直接是 \(Z_i^2\)，但都可以通过标准化转化为卡方分布的定义形式：

• 步骤1：误差正态化：实际问题中的偏差（如 \(X_i-\bar{X}\)、\(O_i-E_i\)），在大样本或正态总体假设下，本身服从或近似服从正态分布；
• 步骤2：误差标准化：将正态偏差减去均值、除以标准差，得到标准正态变量 \(Z_i = \frac{偏差 - E[偏差]}{\sqrt{D[偏差]}}\)；
• 步骤3：求和匹配定义：标准化后的 \(Z_i^2\) 之和，完全符合卡方分布的定义，因此服从 \(\chi^2(n)\) 分布。

关键补充：不满足条件时，平方和不服从卡方分布

如果平方和的构成项不满足“独立+标准正态”，则结果不服从卡方分布：

• 若变量不独立：比如样本误差 \((X_i-\bar{X})\) 之间存在约束 \(\sum_{i=1}^n(X_i-\bar{X})=0\)，因此自由度会损失1，变成 \(\chi^2(n-1)\)；
• 若变量非标准正态：比如偏差服从 \(N(\mu,1)\)（\(\mu\neq0\)），则 \(Z_i^2\) 服从非中心卡方分布，而非普通卡方分布。

四、 总结

1. 应用场景的核心逻辑：卡方分布适配所有需要“量化独立正态偏差累积效应”的问题，从方差检验到信号处理，本质都是对“误差平方和”的分析。
2. 平方和的合理性：不抵消误差、放大关键偏差、数学性质优良、适配正态分布，这四大优势让它成为比绝对值和更优的选择。
3. 分布必然性：卡方分布的定义就是“独立标准正态变量的平方和”，实际问题中的平方和只需经过标准化，就能匹配定义形式——这是“定义→推导→应用”的必然结果。

卡方分布的价值，在于它搭建了“理论分布”与“实际偏差分析”之间的桥梁，让我们可以用严谨的统计学工具，解决生产、科研、工程中的真实问题。