笔记01. 统计推断核心知识点梳理：统计量、参数与三大分布+标准差vs标准误

《回归分析》第一章和第二章~P21。

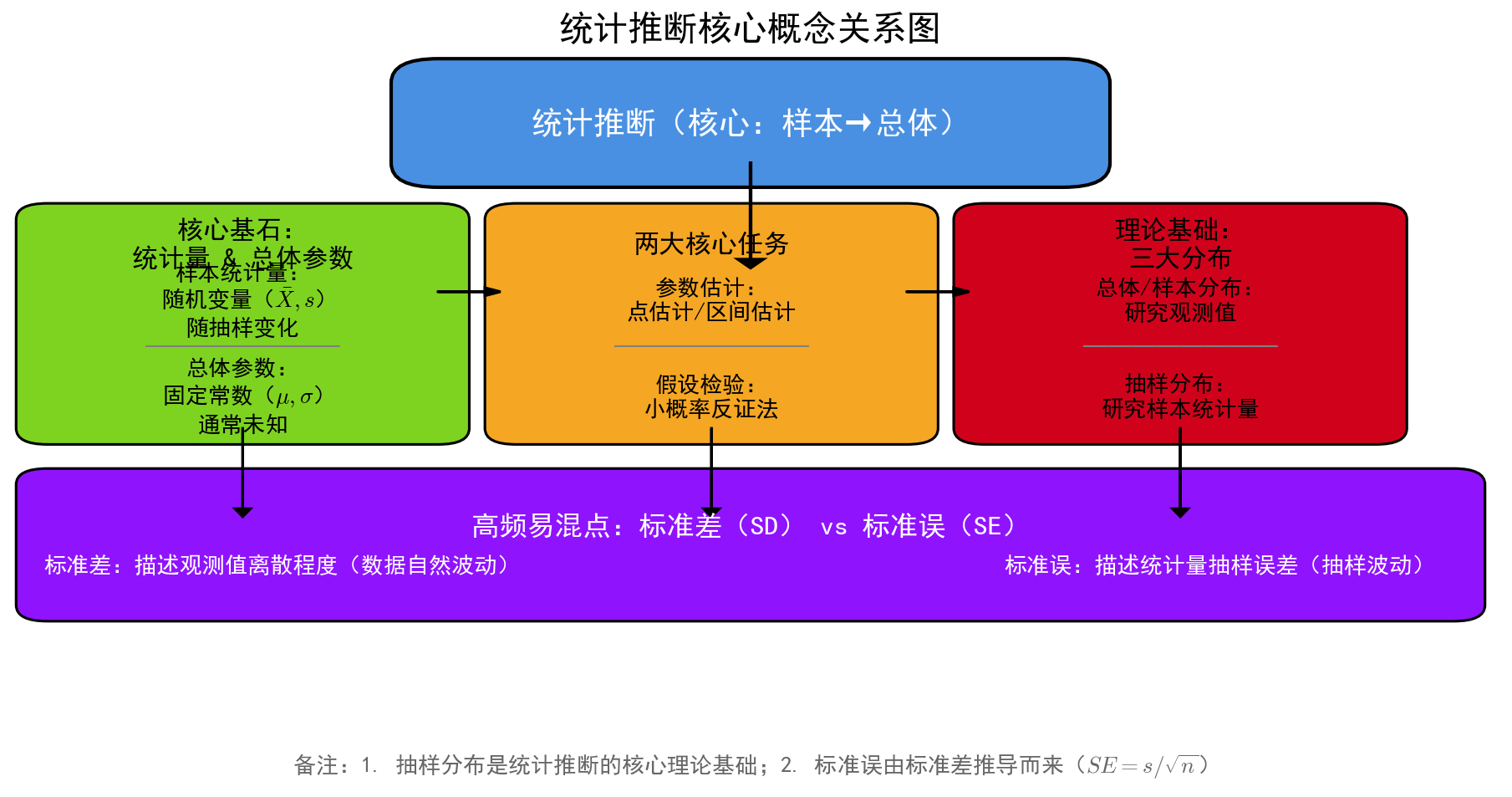
统计推断是统计学的核心逻辑之一，其本质是利用有限的样本数据，对未知的总体特征做出合理的估计和判断，也是从“样本”到“总体”的关键桥梁。本文将系统梳理统计推断的核心基础概念：统计量与总体参数的定义及区别、统计推断的两大核心方法、总体/样本/抽样分布的界定，以及易混的标准差与标准误，帮大家建立统计推断的基础认知框架。

一、核心基石：统计量与总体参数

统计推断的核心动作，是用样本统计量对总体参数进行推断，二者是统计推断中最基础的一对概念，核心区别在于是否随抽样变化、是否已知，先完善核心定义并明确核心属性：
样本统计量是随机变量，每次抽样的结果不同而不同；
总体参数是固定常数，它在研究过程中通常是未知的。

1. 样本统计量（Sample Statistic）

基于抽样样本的观测值计算得到的数值，是对样本特征的描述，也被称为样本特征数。
因为抽样的随机性（同一总体中抽取不同的样本，观测值会存在差异），样本统计量的取值会随样本不同而变化，因此其本质是随机变量。
常见例子：样本均值\(\bar{X}\)、样本方差\(s^2\)、样本比例\(\hat{p}\)、样本标准差\(s\)等，这些都是最常用的样本统计量。

2. 总体参数（Population Parameter）

描述总体整体特征的固定数值，是研究中我们想要探究的“真实值”，属于总体的固有属性。
总体是研究对象的全体，其特征是确定的，因此总体参数是固定不变的常数；但由于总体规模通常较大，我们无法对所有个体进行观测，因此总体参数在研究中通常未知，这也是统计推断的必要性所在。
常见例子：总体均值\(\mu\)、总体方差\(\sigma^2\)、总体比例\(p\)、总体标准差\(\sigma\)等。

3. 统计量与参数的核心对比

维度	样本统计量	总体参数
本质	随机变量	固定常数
取值特性	随抽样样本不同而变化	研究过程中保持不变
可知性	可通过样本数据直接计算	通常未知，需推断
表示符号	拉丁字母（如\(\bar{X},s\)）	希腊字母/固定符号（如\(\mu,\sigma,p\)）
核心作用	推断总体参数的“工具”	统计推断的“目标量”

二、统计推断的两大核心任务

统计推断的所有方法，本质上都围绕样本统计量推断总体参数展开，核心分为两大模块：参数估计和假设检验，二者相辅相成，共同实现对总体特征的推断。

1. 参数估计（Parameter Estimation）

核心目标：基于样本数据计算的统计量，对未知的总体参数给出具体的数值估计或取值范围估计。
简单来说，就是回答“总体参数大概是多少？”的问题，分为两种基本形式：

• 点估计：用单个样本统计量的值作为总体参数的估计值，比如用样本均值\(\bar{X}\)估计总体均值\(\mu\)，用样本比例\(\hat{p}\)估计总体比例\(p\)；
• 区间估计：给出总体参数的一个置信区间，并标注置信水平，比如“95%置信水平下，总体均值的置信区间为(20,30)”，相比点估计，区间估计更能反映抽样的随机性带来的误差。

2. 假设检验（Hypothesis Testing）

核心目标：先对总体参数的取值提出一个假设，再利用样本数据判断这个假设是否“合理”，即是否有足够的统计证据推翻该假设。
简单来说，就是回答“关于总体参数的某个说法是否成立？”的问题，比如“假设总体均值\(\mu=50\)，基于样本数据，这个假设是否可信？”。
假设检验的核心逻辑是小概率反证法：如果一个假设成立时，观测到当前样本结果的概率极小，就有理由推翻这个假设，否则暂时接受该假设。

三、统计推断的理论基础：三大分布（总体/样本/抽样分布）

理解统计推断，必须区分总体分布、样本分布、抽样分布三个概念，其中抽样分布是统计推断的核心理论基础，也是最容易混淆的分布概念，三者的研究对象截然不同，且抽样分布直接决定了统计推断的方法选择。

1. 总体分布（Population Distribution）

定义：总体中所有个体的取值所构成的概率分布，描述了总体取值的整体规律，是总体的固有分布。
研究对象：总体的观测值本身，其特征由总体参数决定（比如总体服从正态分布\(N(\mu,\sigma^2)\)，则\(\mu\)和\(\sigma^2\)是决定该分布的核心参数）。
例子：全校学生的身高构成一个总体，全校学生的身高取值的分布就是总体分布；该分布的均值\(\mu\)是全校学生的平均身高（总体参数）。

2. 样本分布（Sample Distribution）

定义：单次抽样得到的样本中，所有观测值所构成的概率分布，是对总体分布的一次“近似反映”。
研究对象：单次抽样的观测值本身，其形状会随样本不同而略有差异，但样本量越大，样本分布越接近总体分布（大数定律的直观体现）。
例子：从全校学生中随机抽取100名学生，这100名学生的身高取值的分布就是样本分布；该分布的均值\(\bar{X}\)是这100名学生的平均身高（样本统计量）。

3. 抽样分布（Sampling Distribution）

定义：在相同的抽样规则下，从总体中重复抽取大量同容量的样本，对每个样本计算某一样本统计量的取值，这些统计量的取值所构成的概率分布，即抽样分布是样本统计量的分布。
核心关键点：抽样分布的研究对象不是观测值本身，而是样本统计量（如样本均值、样本比例），这是它与总体分布、样本分布的本质区别。
例子：从全校学生中重复抽取1000组样本，每组样本都有100名学生，对每组样本计算身高的样本均值\(\bar{X}\)，这1000个\(\bar{X}\)的取值所构成的分布，就是样本均值的抽样分布。

4. 三大分布的核心对比

分布类型	研究对象	核心特征	与统计推断的关系
总体分布	总体的所有观测值	固定分布，由总体参数决定	统计推断的研究目标分布
样本分布	单次抽样的观测值	随样本变化，近似反映总体分布	统计推断的原始数据来源
抽样分布	样本统计量的取值	统计量的分布，是随机变量的分布	统计推断的核心理论基础，参数估计和假设检验的方法均由抽样分布决定

抽样分布的重要意义

抽样分布揭示了样本统计量的取值规律，让我们可以量化“用样本统计量推断总体参数”的误差大小：比如样本均值的抽样分布服从正态分布（中心极限定理），我们就能基于这一分布计算置信区间、进行假设检验，这也是统计推断从“直观判断”走向“定量分析”的关键。

四、高频易混点：标准差（Standard Deviation）与标准误（Standard Error）

标准差和标准误是统计推断中最易混淆的两个概念，二者均用于描述“离散程度”，但描述的对象、含义、用途完全不同，且标准误与抽样分布直接相关，是统计推断中衡量抽样误差的核心指标。

1. 标准差（SD, Standard Deviation）

定义：描述一组观测值本身的离散程度，反映观测值围绕其均值的波动大小。
分为总体标准差（\(\sigma\)，总体参数）和样本标准差（\(s\)，样本统计量），计算公式分别为：
总体标准差：\(\sigma = \sqrt{\frac{1}{N}\sum_{i=1}^N(X_i-\mu)^2}\)
样本标准差：\(s = \sqrt{\frac{1}{n-1}\sum_{i=1}^n(X_i-\bar{X})^2}\)（\(n-1\)为自由度，用于无偏估计）
核心含义：观测值的“自然波动”，比如学生身高的标准差，反映的是学生身高本身的个体差异大小。
用途：描述一组数据的离散程度，判断数据的波动范围；是计算标准误的基础。

2. 标准误（SE, Standard Error）

定义：描述样本统计量的抽样误差，即样本统计量围绕总体参数的离散程度，本质是样本统计量的抽样分布的标准差。
最常用的是样本均值的标准误（SE of the mean），计算公式为：
\(SE = \frac{s}{\sqrt{n}}\)（当总体标准差\(\sigma\)未知时，用样本标准差\(s\)代替）
核心含义：样本统计量的“抽样波动”，比如样本均值的标准误，反映的是多次抽样中样本均值围绕总体均值的波动大小，即“用样本均值估计总体均值的误差大小”。
用途：统计推断的核心指标，用于计算置信区间、进行假设检验（如t检验、Z检验）；标准误越小，抽样误差越小，样本统计量对总体参数的估计越精准。

3. 标准差与标准误的核心区别

维度	标准差（SD）	标准误（SE）
描述对象	一组观测值的离散程度	一个样本统计量的抽样离散程度
本质	数据本身的波动	抽样误差的大小
与样本量的关系	与样本量无明显关联（样本量足够大后趋于稳定）	与样本量的平方根成反比（样本量越大，标准误越小）
计算公式	样本标准差\(s=\sqrt{\frac{1}{n-1}\sum(X_i-\bar{X})^2}\)	样本均值标准误\(SE=\frac{s}{\sqrt{n}}\)
核心用途	描述数据分布特征	统计推断（置信区间、假设检验）
对应分布	总体分布/样本分布	抽样分布

4. 二者的核心关联

标准误由标准差推导而来，标准差是标准误的计算基础：在样本量固定时，数据的标准差越大，观测值的波动越大，样本统计量的抽样误差也越大，标准误就越大；而在标准差固定时，增大样本量可以显著减小标准误，降低抽样误差，这也是“大样本推断更精准”的数学依据。

五、统计推断核心知识点总结

1. 统计推断的核心是用样本统计量推断总体参数，样本统计量是随机变量（随抽样变化），总体参数是固定常数（通常未知）；
2. 统计推断分为两大核心任务：参数估计（估计总体参数的取值）和假设检验（检验关于总体参数的假设是否成立）；
3. 三大分布的核心区别在研究对象：总体分布/样本分布研究观测值，抽样分布研究样本统计量，抽样分布是统计推断的理论基础；
4. 标准差描述观测值的离散程度，反映数据自然波动；标准误描述样本统计量的抽样离散程度，反映抽样误差，是统计推断的核心指标；
5. 统计推断的所有方法，本质都是基于抽样分布，量化样本统计量的抽样误差，从而实现对总体参数的合理推断。