旅游巴士

旅游巴士
一看题啥也不会

注意到数据点范围，发现有特殊性质 a_i=0 ，也就是说，每个景点没有时间限制，所以在分层图上跑BFS最短路就行了。设 dis[i][j] 为到第 i 个点时，在时刻 t 时刻到达，记录为 t mod k=j，分为 j 层。

考虑正解，假设现在到达了 u 号点，在 t 时刻，要去往点 v，开放时间为 w，如果现在 t >= w，直接通过就行了，到达时间为 t+1。

如果现在 t < w，其实就可以看为，在起点时，往后推移 k 个时间，也就是来景点是的公交车晚上几辆，直到时间 $\geq w$，也就是说等待的时间为 。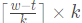

最后就可以用 dijistra 跑一遍分层图最短路，起点是 dis_1,0，终点是 dis_n,0。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m,k,uu,vv,ww,dis[200010][200];
bool vis[200010][200];
struct node{
	ll v,w;
};
struct D{
	ll x,y,w;
	bool operator<(const D &x)const{
		return w>x.w;
	}
};
vector<node> v[200010];
priority_queue<D> q;
int main(){
	cin>>n>>m>>k;
	for(int i=1;i<=m;i++){
		cin>>uu>>vv>>ww;
		v[uu].push_back({vv,ww});
	}memset(dis,0x3f,sizeof(dis));
	dis[1][0]=0;//dijistra跑分层图
	q.push({1,0,0});
	while(!q.empty()){
		ll x=q.top().x,y=q.top().y,w=q.top().w;
		q.pop();
		if(vis[x][y]==1) continue;
		vis[x][y]=1;
		for(int i=0;i<v[x].size();i++){
			ll nx=v[x][i].v,ny=(y+1)%k,nw=v[x][i].w,p=dis[x][y];//nx 为新的节点，ny 表示为新的节点在第 ny 层
			if(vis[nx][ny]==0){
				if(p<nw) p+=(nw-p+k-1)/k*k;//时间不够，原地等待
				if(p+1<dis[nx][ny]){//如果可以松弛，那就松弛
					dis[nx][ny]=p+1;
					q.push({nx,ny,p+1});
				}
			}
		}
	}if(dis[n][0]>=0x3f3f3f3f) cout<<-1;//实在不会可以祈求CCF善良
	else cout<<dis[n][0];
	return 0;
}