2025.2.18的模拟赛“春日” 题解

2025.2.18的模拟赛“春日” 题解

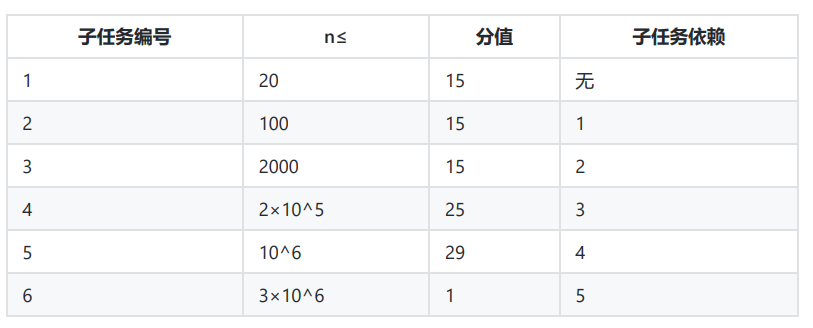
神奇性质题，一堆性质里面随便选几个就可以过，然而我一个都没找到。

先给出性质：

• 最小表示法处一定要断开

• 答案一定是第 \(k\) 小表示法的前缀

• 答案很明显有单调性可以二分

• ……

我们逐一探究。

关于表示法

设以位置 \(i\) 开头的表示法为 \(s_i\)，设表示法 \(s_i\) 的排名为 \(rk_i\)。

结论：当原串的最小循环节为本身时，划分点集合 \(\{i|1\le rk_i\le k\}\) 可以得到答案。

证明（反证法）：我们将第 \(i\) 表示法的划分点到下一个划分点的这段字符串设作 \(t_i\)。假设将 \(t_i(rk_i\le k)\) 换作 \(t_j(rk_j>k)\) 使得答案更优，因为 \(s_j>s_i\) 这种情况发生当且仅当 \(|t_j|<|t_i|\land t_j=t_i[1\sim |t_j|]\) 成立。然而这种情况的成立说明 \(rk_{j+|t_j|}\le k<rk_{i+|t_j|}\) （即 \(j+|t_j|\) 被选了但 \(i+|t_j|\) 没被选），又因为 \(t_j=t_i[1\sim |t_j|]\)，所以 \(rk_j<rk_i\)。这与 \(rk_i\le k<rk_j\) 矛盾，所以原结论成立。

当且仅当原串有更小的循环节时，存在多个 \(rk\) 相等的情况。

• 若循环节个数 \(cnt\le k\)，那么依然不会出现一个没有被选择的 \(rk_j\le k\)，上述结论依然成立。

• 若 \(cnt>k\)，虽然上述结论不成立，但答案显然就是将最小循环节的最小表示法重复 \(\lceil\frac{cnt}{k}\rceil\) 遍。

处理最小表示法需要用 SA，所以最后理论最优复杂度 \(\mathcal O(n)\)，但考场上写个 \(\mathcal O(n\log n)\) 的 SA 不错了。

如果你没有发现这个性质也没关系我们还有别的办法。

作者，作者，你的性质确实很强，但还是太吃注意力了，有没有更加简单又通用的算法推荐一下吗？

有的兄弟，有的。这么强的算法当然是不止一个了。

关于二分

其实根据上述结论，不难得到两个推论：

• 最终答案一定是第 \(k\) 小表示的前缀

• 最小表示法处一定要切断

但是我都上述结论了我还要这两个推论做什么，所以这两个结论还有别的证明方法：

结论一证明：设最终答案为 \(ans\) 第 \(i\) 小表示法的一个前缀为 \(p_i\) （不用知道是哪一个，可以理解为 \(\exists\)）。

• 首先因为存在一种划分点集合为 \(\{i|1\le rk_i\le k\}\)，所以 \(ans\le p_k\)。

• 假设我们有另一种划分方案将原串划分为 \(t_1,t_2,t_3,\cdots t_k\)，这里对其排序使得 \(t_{i-1}<t_i\)，有一个结论是 \(\forall i\in [1,k],t_i\ge p_i\)，用反证法从 \(t_1\le p_1,t_2\le p_2,\cdots\) 开始往后推可以证明。最后得到 \(t_k=ans\ge p_k\)。

于是 \(ans=p_i\)，即答案一定是第 \(k\) 小表示的前缀。

关于第二个性质，依然使用反证法：

假设最小表示法处往后的字符串为 \(s_1\)，往前的那个字符串为 \(s_2\)，若不割，则有 \(s_1'=s_1[2\sim |s_1|],s_2'=s_2+s_1[1]\)，易得 \(s_1\le s_1',s_2<s_2'\) 所以割掉最小表示法处一定更优。

根据第一个性质我们可以二分第 \(k\) 小表示法的的长度然后尝试验证。

如果你没有发现第一个性质也没关系，我们还有别的办法，即直接对所有所有子串二分。

可是子串总共有 \(\mathcal O(n^2)\) 个，这里不能直接二分。

可以先后缀排序，在后缀数组上二分，确定了后缀再在二分这个后缀的前缀。

做到真正的 \(\mathcal O(\log n)\) 可以证明并且已经用c++验证这样是正确的。

二分之后就是如何验证的问题。

根据性质二我们将整个环破成一条链，设待检测的字符串为 \(str\)。

设 \(d_i\) 表示以 \(i\) 开头的最长的字符串使得字典序小于等于 \(str\)，及 \(d_i:=\max\limits_{s[i,j]\le str}\{j\}\)，那么整个问题转化为：通过 \(k\) 个线段覆盖 \(1\sim n\) 是否可行。

不难猜测性质：设用 \(x\) 条线段可以覆盖 \(1\sim n\) 那么 \(x\) 的合法可取集合为一个区间。

设最多用 \(mx\) 个区间进行覆盖，证明就考虑将使用区间数减少，想一个从左往右"跳“的过程，发现转移每次不会存在“必须减少使用两个区间”的情况，即要减少则一定可以减少一个，所以 \(x\) 的合法可取集合一定是个区间。

我们就用 dp 求出 \(mn\) 和 \(mx\) 就行了。朴素转移 \(\mathcal O(n^2)\)，数据结构优化后复杂度 \(\mathcal O(n\log n)\)。

考虑使用刷表法，由于区间左端点是单调的，我们在转移的时候只需要记录右端点的答案，而越靠左的越容易被更新，所以可以发现那些还没有被确定的dp数组时刻是单调的（求 \(mn\) 的时候单增，求 \(mx\) 的时候单减）。发现这就是类似决策单调性的东西。用维护决策单调性的方式维护当前的集合，复杂度 \(\mathcal O(n)\)。

给一个伪代码：

//以求min为例，这是一个暴力 
int dp[NN],d[NN];
void DP(){
    memset(dp,0x3f,sizeof dp);
    dp[0]=1;
    for(int i=1;i<=n;i++){
        int tmp=dp[i]+1;
        if(d[i])for(int j=i;j<=i+d[i];j++)dp[j]=min(dp[j],tmp);
    }
    return;
}
//可以发现[i+1,n]即还没有确定的dp是单调的，我们去维护那些dp，下面是优化后的
struct Node{
    int l,r,val;
};
deque<Node> q;
void DP(){
    q.push_back({1,1,0}),q.push({2,n,INF});
    for(int i=1;i<n;i++){
        while(!q.empty()&&q.front().r<=n)q.pop_front();
        int tmp=q.front().val+1;
        Node nw={i,i+d[i]-1,tmp};
        while(!q.empty()&&q.back().val>=tmp&&q.back().l>=i)q.pop_back();//先是整段的 
        if(!q.empty()&&q.back().r>=i&&q.back().val>=tmp)//再是零散段的 
            q.back().r=i;
        if(!q.empty()){
            if(q.back().r>=nw.r)continue;
            nw.l=max(nw.l,q.back().r+1);
        }
        q.push(nw);
    }
    return;
}

实现中max是从前面取，即·while(q.back().val)>=tmp要换成while(q.front().val<=tmp) 那么就不用双端队列而是用一个栈就实现了。

于是复杂度 \(\mathcal O(n\log n)\)。

如果你没有发现第二个性质也没关系，有更暴力的做法，即直接在环上dp

这与一个问题十分相似：给定圆上若干个弧，询问能否选择 k 个弧覆盖
整个圆。

这个问题是可以 O(n) 解决的：复制一倍断环为链之后，考虑 [l, r] 表示可以从 l
走到 r + 1。对于所有 i 求出从 ≤ i 的位置走一步最多能走到的位置 pi，
令 i 的父亲为 pi。然后我们直接在树上 dfs，用栈记录 k 级祖先，直接
判断即可。

但是两个问题并不完全等价。可以发现：若 di > 0，且覆盖圆使用的最
少弧数量 c ≤ k，则存在选择 k 个位置的方案。

若 di = 0，我们可以把第 i 个字符和顺时针顺序左侧的字符看作一个字
符，然后更新 d，并检查是否有新的 dj = 0 产生。

复杂度 \(\mathcal O(n\log n)\)

——sol