记录
CF1556F Sports Betting
DP、正难则反
首先很明显可以转化为求每个点的获胜概率。
直接考虑获胜的情况,发现由于获胜具有传递性,一个点的全局获胜情况可以会有其他点的局部获胜情况转移得来。
由于每个点有一个权值 \(a_i\),每个点不是等价的,也就是说到达点的不同会影响答案,这里只能将边全部状压,复杂度为 \(\mathcal O(2^{n^2})\)。
点之间的转移是由于“获胜具有传递性”导致的,考虑取其反命题,可以发现"不获胜"不具有传递性,甚至必须同时满足,所以再从不获胜的角度考虑。
全部获胜的概率应该等于 \(1-\) 部分不获胜的概率,可以考虑枚举这个集合。那么就会有一部分获胜一部分不获胜,前者是一个子问题关系,后者由于“必须同时满足”,应该是直接将概率相乘,这是可做的。
剩下就与题解一样了。
所以我认为,“正难则反”其实是因为“正”的时候所满足的一些性质不好处理,而“反”所满足的一些性质截然不同,可能就易于处理了。
CF1734F Zeros and Ones
数位DP,构造不可求类型
很容易转化到这个式子
\(\sum_{i=0}^{m-1}(\bigoplus\limits_{j=0}^{60}\operatorname{bit}[i][j]\oplus\operatorname{bit}[i+n][j])\)
如果直接寻找 \(i\) 的性质,试图进一步化简,发现十分困难。
注意到所有的操作只与数码而不与真实的值有关,并且是计算一段区间的答案,可以考虑数位DP。
有一个式子:\((a\operatorname{bitand}c)\oplus(b\operatorname{bitand}c)=(a\oplus b)\operatorname{bitand}c\)
在处理“构造不可求类型”的题目时,应该尝试将询问转化成另外一个式子。
AGC013E Placing Squares
矩阵快速幂优化DP
很明显这是一道DP题,且需要在连续的非标记段使用矩阵快速幂优化DP。
直接考虑令 \(dp_i\) 表示考虑前 \(i\) 个木板的权值和,有以下式子:
\(dp_i=\sum_{j=0}^{i-1}dp_j(i-j)^2\)
最朴素的想法是,将 \((i-j)^2\) 拆开进行处理,有:
光是 \(a_i\) 的变化,就注定这样用不了矩阵快速幂,因为有 \(i^2a_i\) 与\(2ib_i\) 这两项变量相乘的项,不构成线性变化,怎么办呢?
由于找转移是找相邻元素的关系,我们应该使用“2024.7.11T2”的方法,整体代换成前一项。
我们发现用整体代换的方式去掉的平方,接下来令\(\def\mark{\sum_{j=0}^{i-1}}a_{i}=\mark dp_j,b_{i}=\mark (i-j)dp_j\),有:
-
\(dp_{i+1}=2dp_i+a_i+2b_i\)
-
\(a_{i+1}=a_i+dp_i\)
-
\(b_{i+1}=b_i+a+i\)
可以线性转移
还有一种方法:赋予组合意义,寻求新的解法。
在这里就是“在上面放一个黑球和一个白球的方案数为 \(l^2\),也就对应了原题面中的’平方‘ ”,并转化使用新的线性DP解法,具体如下:

AGC030D Inversion Sum
计数、概率DP
因为一种情况改变的逆序对太多,只想到了 \(\mathcal O(n2^q)\) 的解法
由于这是关心“所有情况的总和”,然而操作对整体的变化太过于复杂,于是转化为局部的考虑。
这里根据期望的定义,化“所有情况的的总和”为逆序对的“期望”乘上方案数,又根据期望的线性,那么转化为求 \(f[i][j]\) 表示最终 \(a[i]>a[j]\) 的概率,就有一个很简单的DP,于是就做出来了。
启示是:求“所有情况的总和"等价于求期望乘上总方案数,就可以利用线性拆贡献。
P4655 Building Bridges
斜率优化DP,动态背包
李超线段树可以通过维护取min后的折线,从而代替线段树维护凸包解决斜率优化DP
CF1194G Another Meme Problem
数位DP
首先一眼数位DP。
但是数位DP是不关心具体数值的,但这道题很明显要关注具体数值。
于是考虑枚举数值大小,易得最终合法的分数值很少,假设最简形式为 \(\frac pq\),那么就枚举\(t\) 计数 \(\frac {pt}{qt}\) 由于需要乘法,只能从低到高枚举,所以需要记录进位以及是否超过上限的后 \(i\) 位,以便统计答案,就做出来了。
如果题目一个点不满足算法前提,可以考虑枚举他
P4590 游园会
状压DP,DP套DP
一个朴素的想法是令 \(f_{i,j,s}\),表示对于前 \(i\) 个位置,已经匹配了 \(NOI\) 的前 \(j,j\in \{0,1,2\}\) 位,并且与奖章串的 LCM 匹配情况为 \(s\) 时的方案数。但是我们发现,仅仅知道匹配的 LCM 的情况是不能得到下一个状态的 LCM 的。这样就无法转移了。
于是想怎么可以在LCM之间转移。
我们知道有一种DP的转移方法:
\(dp_{i,j}=\min(dp_{i,j-1},dp_{i-1,j},dp_{i-1,j-1}+[a_i==b_j])\)
也就是说,只要我们记录 \(dp_{i,*}\) 就可以得到 \(dp_{i+1,*}\) 于是可以考虑将 \(dp_{i,*}\) 放入状态。
但是 \(dp_{i,*}\) 的值 \(dp_{i,j}\in[0,\min(i,j)]\) 并不能直接压位,于是可以考虑压其双射。发现 差分数组 \(c_j=dp_{i,j}-dp_{i,j-1}\in[0,1]\) 直接将 \(c\) 放入状态,实现了状态的表示。
在 \(f_{i,j,dp_{i,*}}\) 之间转移,状态数 \(\mathcal O(n2^k)\) 转移 \(\mathcal O(k)\),总复杂度 \(\mathcal O(nk2^k)\) 剪枝后可通过本题。
P3349 小星星
计数,反演
首先肯定是在树上考虑更简单。
令 \(dp_{i,j,S}\) 表示以 \(i\) 为根的子树上,\(i\) 对应的编号为 \(j\) ,子树选取情况为 \(S\) 的方案数,状态数 \(\mathcal O(n^2\times 2^n)\) ,转移枚举子集,总复杂度\(\mathcal O(n^3\times 3^n)\)。发现是记录 \(S\) 太多了,但不记录的话,转移可能会赋值成相同的编号。
既然限制是必须的,就想能不能通过别的方法代替“通过状态进行”的限制。
利用容斥,转化限制,当有一个较好的全局限制的时候,就可以避免在DP状态中存入过多的信息 。
我们发现“恰好”映射不好做,于是考虑计算“至多”映射,再通过子集反演就可求得
BZOJ4671 异或图
反演
结果恰为 \(1\) 个连通图可以转化为求结果至少为若干个连通图,但之间的关系是什么呢?
令 \(g_i\) 为至少 \(i\) 个连通图, \(f_i\) 为恰好 \(i\) 个连通图,有:
为什么系数是一个斯特林数呢?因为对于一个恰好有 \(i\) 个连通块的方案,我们有 \(\begin{Bmatrix}i\\k\end{Bmatrix}\) 种方法把 \(i\) 个块分到 \(k\) 个子集里面去,所以一个恰好有 \(i\) 个连通块的方案被统计到 \(g_k\) 中的时候会被计算\(\begin{Bmatrix}i\\k\end{Bmatrix}\)次。
根据反演最后的答案为 :
接下来就是考虑如何求出 \(g\)。
由于 \(n,s\) 很小这里可以直接枚举子集划分。子集之间的边就是限制不能选的,我们把这些有限制的边拿出来,用二进制数表示一张图里面有没有这条边,我们要求的就是有多少个图的子集的异或和是 \(0\)。
这是经典的线性基的问题,假如线性基里有 x 个数,答案就是 \(2^{s-x}\)。
时间复杂度 \(\mathcal O(B(n)sn^2)\),其中 \(B(n)\) 为贝尔数,\(B(10)=115975\)。
CF622F The Sum of the k-th Powers
多项式,拉格朗日插值,线性筛
易得原式是一个 \(k+1\) 次多项式,当 \(n\le k+2\) 的时候直接算。否则根据拉格朗日插值有
\(y\) 可以递推求得,总复杂度 \(\mathcal O(k\log k)\)。
可以发现复杂度的瓶颈在预处理 \(\forall j\in[1,k+2],j^k\),怎么快速处理呢?
注意到 \(f(j)=j^k\) 是一个完全积性函数,于是就可以线性筛预处理了。复杂度 \(\mathcal O(k)\)。
找到函数的积性往往可以借助线性筛加速预处理
CF995C Leaving the Bar
归纳、贪心
有一个贪心的思路:
每次随便选取两个向量 \(\vec a,\vec b\) 进行操作,取 \(\vec a+\vec b\) 与 \(\vec a-\vec b\) 中的模长较小值,知道最后只剩下一个向量。
但这样很明显是假的,Hack如下。
3
1000000 0
0 999999
600000 -600000
他的原理是一开始放两个无论如何处理后模长度都很大的向量,让你最后只能爆掉。
乱搞!
为了避免使得两个很大的向量放在一起,可以不断random_shuffle,直到得到正确的结果。然后就过了。
根据归纳的思路,在减小规模的同时不能改变其他的限制,而上述方法却改变的值域的上限。
其实改成一次取三个向量就行了,因为对于任意三个向量,一定会存在两个向量所在直线的夹角小于 \(\frac\pi3\) 此时相加或相减的新向量的模长一定小于等于原来的向量的模长中的较大值,于是可以重复执行这种操作,直到只剩下两个向量,那这两个向量合并后的模长一定 \(\le\sqrt2\times 10^6\) 于是得到答案。
P5298 Minimax
线段树合并
令 \(dp_{x,i}\) 表示节点 \(x\) 取到第 \(i\) 个值的概率,不难列出方程:
复杂度 \(\mathcal O(n^2)\),随机情况下\(\mathcal O(n\log n)\)。并且应该是用线段树合并优化。但是不知道如何合并。
其实合并的时候不一定需要
if(!lt||!rt)return lt|rt;
在这道题中,if(!lt&&rt) 说明 \(i\in tree(rt)\),if(!rt&<) 说明 \(i\in tree(rt)\),分类处理即可。
并且递归的时候可以记录左右儿子信息,便于转移。
P8511 TEST_68
将树转到序列上,对于每个点的答案就是总序列除去中间一段后的两端区间中的最大两数异或。
考虑建可持久化01字典树,但似乎并没有什么好用的处理跨越中间一段的做法。
复杂度 \(\mathcal O(n^2)\)。
发现字典树上的操作是以一个与节点数相关的复杂度插入删除的,于是有一个树上启发式合并的做法:每次先把轻儿子和自己全扔进 trie 然后 DFS 重儿子并保留,接下来遇到一个轻儿子先从 trie 里面删掉这个子树再 DFS 进去,再加回 trie 树,继续 DFS 别的轻儿子。复杂度 \(\mathcal O(n\log n\log v)\),无法通过本题。
考虑全局最值取到的两个点 \(x,y\) 对于子树中不包含这两个点的答案就等于全局答案。只有 \(x,y\) 到根之间的路径上的点的答案不一样,对于这部分,我们从根向下暴力插入或从下往上暴力删除都是可以做的。复杂度 \(\mathcal O(n\log V)\),可以通过本题。
样例不只用来检测你的程序,有时看一看样例(比如这道题,一堆都是 \(15\)),可以给你思路。
最值得到方案又是也是一个关键,特别是全局的最值方案,往往以这个为突破口,可以简化条件。
如果单次询问可能降到更优了,那一定是因为许多答案都是重复的。
P3242 接水果
扫描线,整体二分、链覆盖问题
首先可以转化为一个二位数点问题,然而这里是求第k小,我并没有什么扫描线的方法,所以这里可以使用线段树套线段树套平衡树的方法解决,复杂度 \(\mathcal O(n+p\log^3n+q\log^3n)\) 卡常应该可以通过本题。但是这样写难中难,可以放弃了。
如果每次二分一个 \(x\) 判断比 \(x\) 小的树是否超过 \(k\) 那么就可以使用扫描线了,于是可以使用整体二分来解决,复杂度 \(\mathcal O(n\log^2n)\)
但我写了半个下午才想起来整体二分单次处理不能有设计复杂度的全局变量,只能重构了。
但我又写了半下午没过样例才发现写代码的时候记错题了 QWQ。只能重构了。但有这样一点:
-
一条路径包含多少条路径⇔对应点被多少个矩形覆盖
-
一条路径被多少条路径包含⇔对应矩阵被多少个点覆盖
P2056 捉迷藏
括号序列,先咕一下。
P8253 如何正确地排序
先咕一下。
P5304 旅行者
最短路,二进制划分(不是二进制分组)
本题是要求一个两两之间最短路的最短路,通过建立超级源点的方式可以将求多源最短路化为单源最短路(因为不关心两两间的具体信息)。
然而为了避免从自己走到自己的情况,应该使图划分为两个部分,只计算部分之间的答案。
这就要求任意两个关键点都要分属两边过。
那么对于 \(k\) 个特殊点,我们枚举二进制里的第 \(i\) 位,把二进制第 \(i\) 位是 \(0\) 的点放在 \(A\) , \(1\) 的点放在 \(B\) ,用以上方法跑一个最短路。
原理是,假设 \(k\) 个特殊点里最近的是 \(x\) 和 \(y\) ,那么 \(x\) 和 \(y\) 一定有一个二进制位不一样,那么他们肯定在那次分组的时候被放进了不同的集合,从而肯定被算进了最后的答案之中最短路。
其实还有种方法是随机划分成两部分,一次得到最优解的概率是\(\frac1 4\) 。
假设关键点a到关键点b的最短路径最短,那么当关键点a被分到从源点连边的一半,关键点b被分到向汇点连边的一半时,能够取到最优解,所以概率为1/4。(注意图是有向的)
随机 \(20\) 次,求出最优解的概率就是 \(1-(\frac 34)^{20}\approx99.7\%\),正确性非常高了。
好像还有好几种做法,可以后面研究一下。
ABC077D Small Multiple
同余最短路
“如果你要写风,就不能只写风。你要写柳条轻轻柔柔飘入你心中。”
这道题也是,虽说求的是 \(K\) 的倍数中最大的,但不能只看着这个集合,因为倍数与数位累和并没有什么关系。
因为这是一道数码题,我们要看数值的变化对数码变化的影响。
不考虑进位,那么一个数个位加一,会导致值加一并答案加一。
对于进位,我们可以直接乘十,答案不变。
可以发现从 \(1\) 开始可以计算出所有的正整数。
由于答案自变量集合取于 \(k\) 的倍数,那么数值应该在模 \(k\) 的意义下讨论,直接同余最短路,并且注意到边权只有 \(0,1\) 两种,可以使用 01BFS 复杂度 \(\mathcal O(n+m)\) 。
既然是数码问题,就应该也有数位 DP 做法。
假设位数是有限的,考虑一个不断加数码的过程,设 \(f_{i,j}\) 表示考虑前 \(i\) 位时,模 \(k\) 意义下为 \(j\) 时的最小数码(允许前导 \(0\))。枚举第 \(i+1\) 位填什么,有方程:
枚举 \(i:1\to 1000\) 这个乱搞可以使得你在 \(64\) 个测试点中获得 \(62\) 个 \(\color{Green}AC\)。
当然这是有问题的,因为 \(k\) 可能有无限位,然而这个只能处理有限位的情况。
由于是去最值,一次重复更新没有关系,所以方程可以改为:
这就可以适用于无限的情况。然而这需要解方程。
但我们知道 \(f_1=1\) 所以直接最短路就跑出来了,就转换为了上一个做法。
P4926 倍杀测量者
差分约束
一个Grimgod告诉我的方法:如果贡献以乘积形式累计,可以通过取对数转化为加减
P5905 【模板】全源最短路
太巧妙了。
将 \(0\) 号节点的最短路当作势能,既保证了三角形不等式使得所有节点为正,又使得可以一下转化成最终的正确答案。
关键在于,新增的权值与走的路径没有关系,一条路径就是一个连续的状态变化,设计给每个点赋一个权值,并以差放入答案, 利用叠进和相消,最后就只与初始两种状态有关了。
给每个点赋权值,施以变化累积之相逆变换之正变换,以抵消中间过程,我称其为“势能法”。如果状态变化是通过异或累积,那么\(W(u,v)\leftarrow W(u,v)\oplus h(v)\oplus h(u)\)。如果状态变化是通过乘积累积, 那么\(W(u,v)\leftarrow W(u,v)\times h(v)\div h(u)\)
P7515 矩阵游戏
差分约束、调整法
P3749 寿司餐厅
最小割,最大权闭合子图
当我们连边 \(d_{l,r}\to d_{l+1,r},d_{l,r}\to d_{l,r-1}\),此题变为了一个最大权闭合子图问题,当 \(m=0\) 的时候,直接 \(d_{i,i}\leftarrow d_{i,i}-a_i\) ,跑最大权闭合子图问题即可。
当 \(m\ne 0\) 的时候,代价与选的个数不呈线性关系,但由于 \(m\) 是个常数,直接建立一个新节点就可以了。
P4249 剪刀石头布
网络流,结构解析化
竞赛图三元环的数量为 \({n\choose 3}-\sum_{i=1}^n{in_i\choose 2}\) 。
证明:考虑 \(3\) 个点不构成三元环的情况,必然为一点的入度为 \(2\),一点的出度为 \(2\),一点的入度出度为 \(1\)。不妨从入度入手,一个点若入度为 \(2\),则表明失去了一个三元环,若入度为 \(3\),则会失去 \(3\) 个三元环(考虑点 \(A\) 被点 \(B,C,D\) 通过边指向,那么 \((A,B,C),(A,B,D),(A,C,D)\) 都不会是三元环),因此,对于一个点 \(u\) 而言,记其入度为 \(in_u\),那么点 \(u\) 会使整张图会失去 \({in_u\choose 2}\)个三元环。
差分建图即可。
差分建图:用于处理平方,且希望求最小。
P4843 清理雪道
上下界最小流
建图方式:每条边必须流过一次,即下界。
xht算法:类似有源汇上下界可行流的构图方法,但先不添加 \(T\) 到 \(S\) 的边,求一次超级源到超级汇的最大流。然后再添加一条从 \(T\) 到 \(S\) 下界为 \(0\) ,上界为 \(\infin\) 的边,在残量网络上再求一次超级源到超级汇的最大流。流经 \(T\) 到 \(S\) 的边的流量就是最小流的值。该算法的思想是在第一步中尽可能填充循环流,以减小最小流的代价。
不仅关心网络流的结果,更关心其过程与状态。
Tree MST
最小生成树
有个技巧:
- 对于完全图 \((V,E)\),将 \(E\) 分成 \(E_1 \cup E_2 \cup \cdots \cup E_k = E\))。对每个边集求 最小生成森林,得到新边集 \(E_1^{'}, E_2^{'}, \cdots, E_k^{'}\),再求 MST。最终剩下的边集,等同于原边集的 MST。
此法可减小边的规模。
我们可以点分治,考虑跨越重心的路径所生成的边集。
以分治中心为根,令\(p[u]=w[u]+dep[u]\),则连接两个点的代价就是\(p[u]+p[v]\) (关建边的长度)
我们只需保留p最小的一个点,然后把其他点都和他相连,显然就是MST了。
这里会产生子树内自己连的路径,但是比直接连劣所以不会影响答案。
点分治一共会产生\(O(n\log n)\)条边,然后跑一个kruskal就\(O(n\log^2n)\)
P8078 秃子酋长
回滚莫队
回滚莫队不一定处理无法删除/插入的情况,也可以用于只插入/删除可以减小复杂度的情况。
这题很容易想到以平衡树实现 \(\log\) 的转移。
发现如果只有删除的话,可以用链表 \(O(1)\) 解决。
P8421 rsraogps
扫描线(子区间权值和问题),增量法,势能法
首先这是一个子区间权值和问题,套路扫描线,其实本质就是在看增量贡献,即添加一个元素时,答案如何变化。
扫描 \(r\),为了有前缀相减,令 \(s_i=\sum_{L\le i,R\le r}val(L,R)\)。则答案为 \(s_r-s_{l-1}\)。(扫描线辅助下的子区间前缀化)
考虑增量贡献,即\([i,r+1]\xrightarrow{add\ in} s_i\),在这里要结合性质。
令 \(a'_i=\operatorname{and}_{j=i}^ra_i,b'_i=\operatorname{or}_{j=i}^rb_i,c'_i=\gcd_{j=i}^rc_i\)
\(a',b',c'\) 的变化不会超过 \(\log\) 次,所以 \(a'\times b'\times c'\) 的变化也不会超过 \(O(\log)\) 次,于是可以直接考虑只在发生变化的时候修改,其他时候直接继承。
先考虑不变的时候如何继承。那么在 \(r\) 扩展的时候,\(s_i\) 增加的就是 \(\sum_{j=1}^ival(j,r+1)\) 因为 \(val(j,r)=val(j,r+1)\),所以直接设一个 \(add_i=\sum_{j=1}^ival(j,r+1)\),\(s_i\) 就可以表示为 \(add_i(r-t_i)+v_i\) 其中 \(t_i\) 表示上一次更新的值,\(v_i\) 表示更新的答案。这是随着 \(r\) 的变化自动变化的。
每次扩展暴力找那个不发生变化的位置,根据势能的思路,复杂度 \(\mathcal O(n\log n)\)。
其实势能就是变化的“机会”,操作的增多带来未来操作机会的减少,从而使得一些暴力的复杂度正确。
P5292 校园旅行
DP,删除无意义信息(生成树删边)
首先不难想到一个 \(30\) 分做法,令 \(f_{x,y}\) 表示是否存在 \(x\to y\) 的回文路径。则可以转移,总复杂度 \(\mathcal O(\sum_{x,y}in_x\times in_y)=\mathcal O(m^2)\)。
因为总状态数只有 \(n^2\),许多转移是无效的(即被continue)。转成DFS会WA(但我还不知道为什么,求助帖),考虑如何减少边数!!(一般使用生成树)
我们将所有转移分成两类:向相同编号的点转移(同色边),向不同编号的点转移(异色边)。
对于同色边。如果这些边构成的连通块(同色连通块)是个二分图,那么只保留一颗生成树是等价的,因为边可以来回走,所以一同色边可以选择来回走来等待另一个点的到达。因为在一条边来回走不能改变颜色长度的奇偶性,二分图也是,所以是等价的。
如果不是二分图,说明可以改变的奇偶性,加一条自环即可。
对于异色边。其异色连通块一定是一个二分图,其左右点颜色不同,此时直接生成一棵树一定是对的。
于是通过两次生成树,将边数缩小至 \(2n-2\) 以内(一次生成树有 \(n-1\) 条边)。
复杂度 \(\mathcal O(n^2)\)。
P5363 移动金币
博弈论,计数DP
可以发现这是一个变相的阶梯NIM,满足:
于是设 \(dp_{i,j,opl}\) 表示考虑前 \(i\) 个变量,和为 \(j\) ,异或结果为 \(opl\) 的方案数,分 \(i\) 的奇偶转移即可。复杂度 \(\mathcal O(n^3m)\)。
注意到两点:
-
变量是等价的,所以可以直接用组合数解决,不必要以\(\mathcal O(m)\)的复杂度枚举解决。
-
考虑不为 \(0\) 的,可以是总数减去为 \(0\) 的,这在 NIM 相关的组合数问题中常见。
因为异或和为 \(0\),其每一位都应该只有偶数个位置为 \(1\),确定哪些数的第 \(i\) 位为 \(1\),可以使用组合数计算。
设 \(f_{i,j}\) 表示考虑二进制前 \(i\) 位,元素和为 \(j\) 的方案数,有:
\(
\begin{aligned}
f_{i,j}\xleftarrow{+}f_{i-1,j-k\times 2^i}\times {\lfloor \frac{m+1}2\rfloor\choose k}&&2|k
\end{aligned}
\),最后用插板法在考虑偶数项, \(res\xleftarrow+f_{\log_2(n-m),i}\times {n-i-\lfloor \frac{m+1}2\rfloor\choose m-\lfloor \frac{m+1}2\rfloor}\),答案为\({n\choose m}-res\),复杂度 \(\mathcal O(n\log n)\)。
P3642 烟火表演
slope trick
以这道题为例探讨一般情况下 slope trick 做题思路。
列出方程
找到一个朴素的 DP 方程,并使得这个转移是一个状态被包含进绝对值。
这个函数一定形如下图:
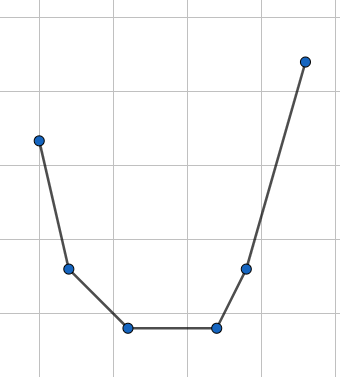
本题中,令 \(dp_{x,i}\) 表示以 \(x\) 为根的子树中,到所有叶子的时间为 \(i\) 时的最小代价,可以得到朴素方程 \(dp_{x,i}=\sum_{y\in \operatorname{son}(x)}\min_{j\le i}dp_{y,j}+|w-(i-j)|\),其中 \(w\) 表示 \(x\to y\) 的边权。
拆绝对值
以函数斜率为零的最低段 \([L,R]\) 入手,把绝对值拆成分段函数的形式,并直接确定函数的取值位置。
考虑从一个节点到父亲节点的转移。
-
当 \(i\le L\) 的时候,由于移动 \(j\to j-1\) 会使 \(dp_{y,j}\) 增加 \(\ge 1\) (斜率 \(\le-1\)),而\(|w-(i-j)|\) 无论如何增加的值 \(\le 1\)。所以 \(j=i\) 取到最小值,\(g(i)=f(i)+w\)。
-
当 \(L\le i\) 的时候,根据上文的分析,一定是 \(j\in [L,R]\) 的时候取到最小值,于是考虑后面的权值如何取到最小。很明显我们想让 \(w-(i-j)=0\) 即 \(j=i-w\)。
-
当 \(j=i-w\in [L,R]\) 即 \(i\in [L+w,R+w]\) 的时候,有 \(g(i)=f(L)\)
-
当 \(j=i-w<L\) 即 \(i\in [L,L+w)\) 的时候,\(|w-(i-j)|=w-i+j\),我们想让值最小,就要让 \(j\) 尽量小,所以 \(j=L,g(i)=f(L)+w-i+L\)。
-
当 \(j=i-w>R\) 即 \(i\ge R+w\) 的时候, \(|w-(i-j)|=i-w-j\),同理要让 \(j\) 尽量大,所以 \(j=R,g(i)=f(R)+i-w-R\)。
-
综上所述:
合并函数
函数直接相加,可以直接将端点合并,不去重,注意维护新的 \(L,R\)。
直接暴力的用 multiset 都可以,但一般情况下只需要用可并堆,因为我们并不想要随机访问,一般是从左到右或从右到左顺序遍历。
维护端点
根据得到的分段函数,维护斜率变化位置的横坐标,相邻段变化为 \(1\)。
首先要得到 \(L,R\) 的具体值,对于一般情况,可以手动维护,并将 \(L\) 左侧,与 \(R\) 右侧分开来,比如 NarrowRectangles 这道题。
但这里不用,观察性质,每一个处理的函数 \(R\) 右侧是无限远的斜率为 \(1\) 段。假设一个点有 \(k\) 个儿子,那么 \(R\) 右边总共有 \(k\) 个段,存储了 \(k-1\) 个端点。直接弹出即可(反正我们不需要,都要覆盖为斜率为 \(1\))。
计算答案
从 \(f(0)\) 算起,往右边走。
假设第 \(i\) 个端点为 \(a_i\), \(a_x=L,a_1=0\),则 \(ans=f(0)-\sum_{i=2}^x(a_i-a_{i-1})\times(x-i+1)=f(0)-\sum_{i=1}^xa_i\)。
对于本题, \(f(0)=\sum w\)。
P5445 路灯
树套树(二维数点),费用提前计算
首先可以注意到每次的 \(1\) 段构成了一段一段极大连续区间,每个秒对于一个极大连续区间的所有子区间加 \(1\)。于是我们可以进行维护,并转化为一个二位数点问题,每次相当于执行矩阵 \(+1\) ,单点查询,但是每次的举行可能太多了。
可以费用提前计算!
假设一个矩形在 \([t_1,t_2]\) 区间中存在,对于时间 \(t\in [t_1,t_2]\),我们可以对矩形加上了 \(t-t_1\) 于是可以在 \(t_1\) 时刻减去 \(t_1\),\(t_2\) 时刻加上 \(t_2\),对于中间的时候惊醒判断是否被包括在矩形中,如果是加上 \(t\) 即可。
P5336 成绩单
区间DP
很明显是一个区间DP,于是设 \(f_{l,r}\) 表示 \([l,r]\) 的最小答案,尝试转移,但发现区间不一定全部去除,可能留有一部分,于是记录 \(g_{l,r,mn,mx}\) 表示 \([l,r]\) 区间中,剩下最大值为 \(mn\),最小值为 \(mx\) 的最小权值,发现并不好枚举子区间进行转移,因为不知道还剩下那些数,不能选取一些数的同时保留另一些数。
既然不能同时取,那就分别处理,先合并,再计算贡献,有以下转移:
复杂度 \(\mathcal O(n^7)\)。
可以按照右端点的情况讨论:
-
\(r\) 已产生贡献:\(g_{l,r,mn,mx}=\min\limits_{l\le k<r}g_{l,k,mn,mx}+f_{k+1,r}\)
-
\(r\) 未产生贡献:\(g_{l,r,mn,mx}=\min\limits_{\min(mn',w_r)=mn,\max(mx',w_r)=mx}g_{l,r-1,mn',mx'}\)
-
这次产生贡献:\(f_{l,r}=\min_{mn,mx}(g_{l,r,mn,mx}+a+b(mx-mn)^2)\)
复杂度 \(\mathcal O(n^5)\)。
如何第二条转移的计算复杂度:,有 \(\mathcal O(n^2)\) 个状态需要 \(\mathcal O(n^2)\) 的代价转移,有 \(\mathcal O(n^3)\) 个状态需要 \(\mathcal O(n^3)\) 需要 \(\mathcal O(n)\) 的代价转移,有 \(\mathcal O(n^4)\) 个状态需要 \(\mathcal O(n)\) 的代价转移,所以总复杂度为 \(\mathcal O(n^4)\)。
其实第二条转移可以直接用刷表法简单转移:\(g_{l,r,mn,mx}\to g_{l,r+1,\min(mn,w_r),\max(mx,w_r)}\)
原因是最值操作不可逆,刷表法是顺向操作,自然更符合。
P4563 守卫
区间DP
首先注意到对于每个区间,右端点是必选的。
记 \(p\) 是 \(r\) 可以看见的最左端那么其将区间分成了两个部分,则 \(f_{l,r}=\min(f_{l,p},f_{l,p-1})+f_{p+1,r}\)。
我们可以更改枚举顺序,每次固定 \(r\),扩展 \(l\),那么 \(p\) 就能顺便扩展出来。
复杂度 \(\mathcal O(n^2)\)。
P2481 代码拍卖会
DP,拆分贡献
有一个朴素 DP:\(f_{i,j,p}\) 表示考虑第 \(i\) 个位置,上一个位置的值为 \(j\),数 \(\bmod P=p\) 的方案数,直接转移:\(f_{i,j,p}\xrightarrow{k\ge j}f_{i+1,k,(10p+k)\bmod P}\)。复杂度 \(\mathcal O(bnp),b=9\)
将转移看作 \(f_{j,p}\xrightarrow{k\ge j} f_{k,(10p+k)\bmod p}\) 的变化,并将 \(\{j,p\}\) 看作一维向量,那么这就可以手动打满转移矩阵(而不是手推),使用矩阵快速幂优化。
复杂度 \(\mathcal O(b^3p^3\log n),b=9\)。
发现转移的问题在于,我们不得不从左往右处理并记录上一位选择了什么,来限制这一位的转移,即数位的选择相互牵制,如果可以将贡献拆开,化为简单的情况,就可处理了(就像《成绩单》那道题,拆为选完与没选完两种)。
注意到对于任何一个方案,都可以看做 9 个以内的若干 “1 的后缀”相加而成!如下图:

于是我们只需要随便找九种并起来就好了,这样就没有了选择的限制。
考虑将 \(\bmod P\) 意义下相等的数看作同一类。记 \(g_i\) 为 \(\bmod P\) 意义下余数是 \(i\) 的“1 的后缀”的数量,这很明显是由循环节的,且长度不超过 \(P\)。
接着做一个背包就好了。设 \(dp_{i,j,p}\) 表示当前考虑到余数为 \(i\) 的 “1 的后缀”,此前已经放上了 \(j\) 个“1 的后缀”,此时构成的数字的 \(\bmod p\) 的余数是 \(p\) 的方案数。
有转移方程:\(dp_{i,j,p}\times {g_i+s-1\choose s}\to dp_{i+1,s+j,(p+s\times i)\bmod P}\)。
复杂度 \(\mathcal O(b^2p^2)\)。
P5385 须臾幻境
主席树,LCT
准备型离线(假离线):强制在线时,也可使用离线算法进行预处理,并并记录离线处理时的各个状态(本题是主席树),此时不是直接得到答案,而是为快速得到答案做准备。
其实点分树也是一种假离线,但莫队就不要想了。
如果可以离线,那么有 \(\mathcal O(n\sqrt n\log n)\) 的回滚莫队加并查集实现。
在不预处理的情况下,易得单次询问的时间复杂度不可能低于 \(\mathcal O(n)\) 。(因为最多可能有 \(n-1\) 条边“生效”)。
那么如何预处理呢?考虑假扫描线。
每次从右往左扫 \(r\),对于询问来说,\(r\) 一定的情况下,\(l\) 越靠左,所包括的边集严格更多。即出现环的时候,应该抛弃环上编号最靠前的边。这可以用 LCT 解决。
因为连通块的个数\(=\)点数\(-\) 生成森林的边数,所以可以用一个线段树动态维护那些边是在 LCT 中的,因为是假离线,需要主席树。
P5979 Druzyny
CDQ优化DP
使用场景:DP转移不连续,考虑贡献。
过程:利用分治,考虑 \(\forall j\in[l,mid],i\in [mid+1,r]\),考虑 \(j\to [mid+1,r]\) 与 \([l,mid]\to i\)。即分开考虑。
过程:\([l,mid],[l,mid]\to [mid+1,r],[mid+1,r]\) 重点在中间
不难得到一个朴素的 DP 方程:\(dp_{i}\) 表示以 \(i\) 作为结尾划分的最大值为多少,有 \(dp_{i}=1+\sum_{j\le i\land i-j\in[mx_{j+1,i},mn_{j+1,i}]}dp_j\)。其中\(mn_{l,r}=\min_{i=l}^rd_i,mx_{l,r}=\max_{i=l}^rc_i\)DP 求最值的方案数是套路的,这里的问题是, \(j\) 的转移并不连续,无法通过往常的方法优化。
考虑每个 \(j\) 对 \(i\) 的贡献,记为 \(j\to i\),那么可以使用 CDQ 将变为整体之间的贡献,加速计算。
考虑如何求出 \([l,mid]\to[mid+1,r]\)。我们将 \(mn_{j+1,i}\) 拆分为两块,即 \(mn_{j+1,mid+1},mn_{mid+1,i},mx\) 同理,这样就变为了一个一元变量。那么条件变为:
- \(mx_{j+1,mid+1}\le i-j\le mn_{j+1,mid+1}\implies i\in[mx_{j+1,mid+1}+j,mn_{j+1,mid+1}+j]\)
- \(mx_{mid+1,i}\le i-j\le mn_{mid+1,i}\implies j\in[i-mn_{mid+1,i},i-mx_{mid+1,i}]\)
需要同时满足。
第二个条件直接线段树维护,第一个条件可以使用类似扫描线的方法解决,即动态加入删除。
于是做到了复杂度 \(\mathcal O(nlog^2n)\)。
P7914 括号序列
区间DP
直接把所有情况列出来
-
**** -
(...) -
(...)...(...) -
***(...)...(...) -
(...)...(...)***
区间 DP 转移即可。
P3592 MYJ
区间DP
CDQ 与区间 DP
划分区间使得独立的问题不仅可以使用 CDQ,而且可以使用区间 DP
其中 CDQ 分治是考虑两侧元素之间的点对点贡献
而区间DP是只关心整体值
但他们使用前提相同——区间可划分 。
这道题想到了 CDQ 就应该也往区间 DP 想一想。
P10656 学习轨迹
扫描线,估计答案上下界
首先有一个暴力,如果枚举 \(a\) 的选择区间,那么这些数在 \(b\) 中的位置会将 \(b\) 分为若干段,我们应该选取最大的那一段,这个可以确定 \(l\),扩展 \(r\) 的同时用 set 维护,复杂度 \(\mathcal O(n^2\log n)\)。也可以反过来化添加为删除,用链表维护,复杂度 \(\mathcal O(n^2)\)。
因为是求最大值,可以尝试对答案估计下界,发现答案一定不会小于 \(\max(\sum a,\sum b)\)。那么在枚举区间处理的时候仅当 \(\sum_{i=l_1}^{r_1} a_i+\sum_{i=l_2}^{r_2}b_i>\max(\sum a,\sum b)\) 的时候答案可能产生贡献。那么 \(\sum_{i=l_1}^{r_1} a_i>\frac{\sum a}2\) 或 \(\sum_{i=l_2}^{r_2} b_i>\frac{\sum b}2\)。也就是说一定包含 \(a\) 或 \(b\) 的加权中点 \(p\)。
联系到上面的暴力算法,我们发现根本不需要用链表维护整个序列的选取情况,而仅仅只需要关心 \(p\) 所在的那一段。
于是将暴力算法改进为,对 \(a\) 扫描线,动态维护 \(s_l\) 表示 \([l,r]\) 的答案,发现 \(p\) 所在的段左边界递增,右边界递减,可以用单调栈加上区间赋值线段树解决。
复杂度 \(\mathcal O(n\log n)\)。
注意:线段树的区间修改的下传标记必须要使用一个 \(tag\) 实现,与父节点的信息进行“同步”的做法是错误的,因为父节点的信息本身就应该由叶子节点得到,不应该由此反推。
P10208 礼物交换
广义前驱后继:满足条件的元素中编号之左右最邻近点,以确定包含自己的区间中的其他点是否有满足条件的。就是将关心所有点变为关心最有可能满足条件的那个点
临界点思想:从关心所有点变为关心最容易使得条件成立或不成立的那个点。
比如这个“广义前驱后继”和 \(\forall i<a\implies \max _i<a\) 的方法
条件转化从简思想:区间中满足条件A的可以\(\implies\) 满足条件A中属于区间的
同时满足条件AB \(\iff\) 满足条件A中满足条件B的 \(\iff\) 满足条件B中满足条件A的
不难发现,组合是可行的当且仅当 \(\forall i\in [l,r],\exists j\in[l,i)\cup(i,r],B_j<A_i\land A_j>B_i\)。
讲条件转化为 \(\forall i\in [l,r],\sum_{A_j>B_i}1-\sum_{B_j>A_i}1>1\),这里 \(j\) 可以等于 \(i\),可以做到复杂度 \(\mathcal O(nq)\)。
但第二个条件似乎没有第一个条件“简洁”。其实,将每一个元素看作区间 \([B,A]\) ,第一个条件其实就是有区间与它相交!
\(\forall i\in[1,n]\) 求出 \(L_i:=\max_{j<i\land B_j<A_i\land A_j>B_i} j,R_i:=\min_{j>i\land B_j<A_i\land A_j>B_i}j\)。
那么条件一转化为:\(\forall i\in [l,r],L_i\ge l\lor R_i\le r\)。
即 \(\nexists i,L_i<l\le i\le r<R_i\),于是就变为了 \(l\in [L_1+1,i],r\in[i,R_i-1]\) 的二位数点问题,且没有了特别的对范围 \(i\in [l,r]\) 的考虑。
这个用树状数组解决,复杂度 \(\mathcal O(n\log n)\)。
还有一种暴力:
如果 \(x\) 可以给 \(y\) 那么连边 \(x\to y\)。最后判断是否每个点都在环上。
不难看出一个将序列按照 \(A\) 排序后,一个一定是向一个区间连边(即一个区间是可行的),差分即可,复杂度为 \(\mathcal O(nq\log n)\)。
这个方法也可以用同样的方法用广义前驱后继优化到 \(\mathcal O(n\log n)。\)
P10207 马拉松比赛 2
区间DP,DP剪枝,诈骗题
为了不负重折返跑,易得对于一个 \(G\) 来说,距离 \(G\) 远的一定比距离 \(G\) 近的先拿起来,即不论询问是什么,没有拿起来的一定形如一个区间 \([l,r]\),对于一个具体的询问 \(G\) 来说 \(l\le G\le r\)。
发现无论如何, \(S\) 一定要跑到最左或者最右边的时候,才开始捡起工作,且最后捡完后才走向 \(G\) 所以捡起顺序的选择及最小代价与 \(S,G\) 无关,最后加上即可。
发现在不断捡起的过程中区间的状态发生变化,于是考虑使用 DP 转移。
对 \(x\) 排序,设 \(f_{l,r,0/1,0/1}\) 表示区间 \([l,r]\) 的小球不捡,其余捡起,此时处于\(l/r\),且一开始先去到最左/右的小球,的最小代价,有转移:
边界:\(f_{1,n,c,c}=1,c\in\{0,1\}\)。
复杂度 \(\mathcal O(n^2+q)\)。
复杂度肯定过不了了,考虑剪枝。
假如对序列去重后有 \(k\) 个点,那么答案至少就是 \(\sum_{i=1}^ki=\frac{(k+1)k}2\),因为 \(t\le 5\times 10^5\),所以 \(k\ge10^3\) 的时候全部输出“NO”(诈骗题中的数据范围利用!)。然后就过了。
P4755 Beautiful Pair
CDQ 分治
尽量将关心的内容降到最少
因为是所有对数,并且一对关心的还是一个区间,所以考虑过扫描线,但是由于加上了 \(\times a_i\) 导致对于不同的位置有着不同的变化,很难统一考虑,失败了。
看似是关心一个区间,其实只关心区间内的最大值,当区间的最大值确定的时候,两边相互的限制就简单了。
并且这又是一个关心两两组合的问题,可以考虑 CDQ 分治。
每次找到一个区间的最大值,递归两边,并是两边分别有序,最后 upper_bound 进行查找就行。
复杂度 \(\mathcal O(n\log^2n)\)。
注意事项:在不完全二分中(即不是从中间剖开),\(\mathcal O(n)\) 遍历的复杂度是不受保障的。唯一正确的方法就是启发式分裂。
P4707 重返现世
容斥
首先根据 k-min-max 容斥,令 \(k\leftarrow n+1-k\),题目其实就是要求:
重点在如何计算这个容斥式子。
考虑增量法,即新添加一个 \(p_i\) 考虑系数变化。很明显要记录一个值 \(j\) 表示原来的 \(\sum p\) 值,\(j\leftarrow j+p_i\)
设 \(o=(-1)^{|T|+k}{|T|-1\choose k-1}\),发现当 \(|T|\leftarrow |T|+1\) 的时候,\(o\leftarrow -\frac{|T|+k-1}{|T|}o\) 发现这个值并不是一个定值,也就是说对于不同的 \(|T|\) 有着不同的转移系数,失败了。
考虑另一条路,即递推式,有 \((-1)^{|T|+k+1}{|T|\choose k-1}=-(-1)^{|T|+k}{|T|-1\choose k-1}+(-1)^{|T|+k-1}{|T|-1\choose k-2}\)
可以发现整个变化只与 \(k\) 有关,而这是 \(k\le 10\),所以完全可以记录,且对于不同的 \(|T|\),这样的转移都是成立的。
于是设 \(dp_{i,k,j}\) 表示加入考虑 \(p_i\), \(k,j\) 为状态时的转移系数。有转移:\(dp_{i,k,j}=dp_{i-1,k,j}+dp_{i-1,k-1,j-p_i}-dp_{i-1,k,j-p_i}\)。
关于边界,有结论:\(\forall i,dp_{i,0,0}=1\)。
证明:要考虑 \(T=\emptyset\) 时对 \(dp_{i,k,p_i}\leftarrow dp_{i-1,k-1,0}\) 的影响(组合意义为添加第一个数),很明显此时需要 \(dp_{k,i,p_i}\leftarrow (-1)^{k+1}{0\choose k-1}\) ,这个式子只在 \(k=1\) 的时候有值 \(1\),所以边界就需要使 \(dp_{i,1-1,0}=dp_{i,0,0}=1\) 其余的为 \(0\)。
本体可解的一个很大原因是 \(k\le 10\),不然就需要与 \(o\leftarrow -\frac{|T|+k-1}{|T|}o\) 记录一样的情况数 \(1000\)。一定要注意“小量”。
找到转移的统一性。
P9910 Dizalo
树状数组
研究生效时间
组合意义与表达式的转化
不难分析出,答案为对于所有后缀最小值的位置,前面比其大的数的个数之和,利用单调栈,可以做到 \(\mathcal O(nq)\) 。
首先考虑一个值什么时候成为后缀最小值,我们发现,只有当它后面比它小的数全部删除,并且自己没有被删除的时候,它是后缀最小值,于是我们发现一个值是后缀最小值的时间是一个区间!(研究生效时间!)
假设此时后缀最小值的集合为 \(S\),即 \(\sum_{j\in S,i\in U}[a_i>a_j\land i<j]\)。
这是一个二维数点问题,可以用数套树 \(\mathcal O(q\log^2n)\) 解决。
因为 \(\forall i>j,j\in S,a_i>a_j\),所以原式等于 \(\sum_{j\in S}[a_i>a_j]-[i>j]\),直接树状数组就可以了。复杂度 \(\mathcal O((q+n)\log n)。\)
尝试过单侧递归线段树,失败了,表现为无法与权值修改相结合,本质是没有对题目的性质进行进一步挖掘,改进方法为多角度的考虑问题,在多种性质间转化。
P10137 Walking in Manhattan G
倍增
只看结果,不问过程:如果变化的过程很复杂,那么尝试直接枚举+判定结果。
因为交点有 \(O(n^2)\) 个,所以一定要从线的角度考虑
需要发现一个性质,时间其实可以转化为线的奇偶性,如果线条的奇偶性相同,则不换方向,否则一定换方向。
并且换了方向后一定是一上一右交替,于是可以将奇偶性相同的线看作一段,我们枚举一上一右交替次数进行判定,这样就没必要知道到底经过了那些位置,直接可以处理出最终到哪里。发现这个枚举可以用倍增代替,复杂度 \(\mathcal O(n\log n)\)。
P10138 Cowmpetency G
首先发现线段不能完全重叠,然后剩下没什么难的。
可以考虑化为形式化语言,进行思考。
P10191 Test Tubes S
应该先找到结束情况
-
两个烧杯中各有一互异颜色(此时不用再倒向烧杯)
-
有一只没有颜色。
容易发现烧杯中只能放一种颜色,直接枚举放哪种,避免讨论。
然后模拟整个过程,需要注意当试管顶元素相同的时候,因为最后要减成各只有不超过一个颜色,所以应该是颜色多的向颜色少的倾倒。
P1052 过河
因为根据 \(\text{Theorem 1}\),一个点可以跳到里自己距离大于 \(71\) 的所有点,那么两个石子的距离超过 \(71\) 是没有必要的,于是 \(a_i-a_{i-1}\leftarrow \max(a_i,a_{i-1},71)\)。直接暴力DP即可。
还有一个想法是矩阵加速。
因为一个 \(i\) 状态可能由前面 \(i-t\sim i-s\) 状态得来,于是可以将\(i-t\sim i-1\) 这些状态压作一个向量,设计一个 \(t\times t\) 的矩阵,复杂度 \(\mathcal O(t^3m\log L)\)。
P2051 中国象棋
计数DP
一切无标号的东西都不用状压,而是计数,即等价不区分。
首先很容易想到一个状压的做法,但是列是无标号等价的,所以直接记录有列选了 \(1\) 个,几列选了 \(2\) 个,既可以转移了。
P2516 最长公共子序列
计数DP
小容斥,直接剪掉不合法
发现算重只会在 \((i,j-1)\) 与 \((i-1,j)\) 中,而重复区间为 \((i-1,j-1)\),所以减去即可。
P9871 天天爱打卡
离散化
离散化的值是需要的值,而不一定是真正存储的值。比如这道题,将l-1离散化,因为这是“需要的值”,一定要想清楚。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号