ABC 273 C (K+1)-th Largest Number
题意:
给予你一个长度是N的数组a,对于每一个k(0,1,2,... N - 1), 完成一下问题:
找到1 ~ N中的数字a[i],找到大于a[i]的数目恰好是k个不同数的个数
思路:通过二分找到的每一个元素a[i]在数组a中有多少个不同的元素大于a[i]
时间复杂度:O(nlogn)
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int a[N];
map<int, int> mp;
int st[N];
int main() {
int n;
cin >> n;
vector<int> vt;
int x;
for (int i = 1; i <= n; i ++ ) {
scanf("%d", &a[i]);
vt.push_back(a[i]);
}
sort(vt.begin(), vt.end());
vt.erase(unique(vt.begin(), vt.end()), vt.end());
// for (int i = 0; i < vt.size(); i ++ ) {
// cout << vt[i] << " ";
// }
// cout << endl;
for (int i = 1; i <= n; i ++ ) {
int ans = 0;
int l = 0, r = vt.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if(vt[mid] >= a[i]) r = mid;
else l = mid + 1;
}
ans = vt.size() - l - 1;
st[ans] ++ ;
}
for (int i = 0; i < n; i ++ ) {
cout << st[i] << "\n";
}
return 0;
}
ABC 273 D LRUD Instructions
题意:
在一个矩阵中,你在(r, s)的位置上,根据给定的指令输出你在一个指定指令上可以到达的位置,同时矩阵中存在一些障碍物,遇到障碍物无法再次移动
思路:用map<int, vector
时间复杂度:O(qlogn)
代码:
#include <bits/stdc++.h>
using namespace std;
int h, w, n, r, c, q;
map<int, vector<int> > amp, bmp;
//用于横向和纵向的记录每一个障碍物的位置
int main() {
cin >> h >> w >> r >> c >> n;
for (int i = 1; i <= n; i ++ ) {
int rr, cc;
cin >> rr >> cc;
amp[rr].push_back(cc), bmp[cc].push_back(rr);
}
//值得记忆
for (auto &p : amp) sort(p.second.begin(), p.second.end());
for (auto &p : bmp) sort(p.second.begin(), p.second.end());
cin >> q;
char d;
int l;
for (int i = 1; i <= q; i ++ ) {
cin >> d >> l;
if(d == 'L') {
auto it = amp.find(r);
int Ib = 0;
if(it != amp.end()) {
vector<int> &vec = it -> second;
auto it2 = lower_bound(vec.begin(), vec.end(), c);
if(it2 != vec.begin()) it -- , Ib = *it2;
c = max(c - 1, Ib + 1);
}
} else if(d == 'U') {
auto it = bmp.find(c);
int Ib = 0;
if(it != bmp.end()) {
vector<int> &vec = it -> second;
auto it2 = lower_bound(vec.begin(), vec.end(), r);
if(it2 != vec.begin()) it2 -- , Ib = *it2;
}
}
if(d == 'R') {
auto it = amp.find(r);
int ub = w+1;
if(it != amp.end()) {
vector<int> &vec = it->second;
auto it2 = upper_bound(vec.begin(), vec.end(), c);
if(it2 != vec.end()) ub = *it2;
}
c = min(c+l, ub-1);
}
if(d == 'D') {
auto it = bmp.find(c);
int ub = h+1;
if(it != bmp.end()) {
vector<int> &vec = it->second;
auto it2 = upper_bound(vec.begin(), vec.end(), r);
if(it2 != vec.end()) ub = *it2;
}
r = min(r+l, ub-1);
}
cout << r << " " << c << "\n";
}
return 0;
}
ABC 272 C Max Even
题意:
给予你一个长度为n的数组A,确定是否存在一个偶数是数组A中两个数的总和,如果存在就输出最大的偶数,如果不存在就输出-1
思路:将数组中的奇数和偶数分开,连个奇数可以合成一个偶数,两个偶数可以合成一个偶数,依次知道最大的偶数(此时的0可以归在偶数里)
时间复杂度;O(n)
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int a[N];
int n;
int b[N];
bool cmp(int a, int b) {
return a > b;
}
int main() {
cin >> n;
int ans = 0, res = 0;
int sum = 0;
for (int i = 1; i <= n; i ++ ) {
int x;
cin >> x;
if(x % 2 == 0) a[ ++ ans] = x;
else b[ ++ res] = x;
}
sort (a + 1, a + 1 + ans, cmp);
sort (b + 1, b + 1 + res, cmp);
if(ans <= 1 && res <= 1) cout << -1 << endl;
else {
if(ans <= 1 && res > 1) {
cout << b[1] + b[2] << endl;
}
else if(ans > 1 && res <= 1) {
cout << a[1] + a[2] << endl;
}
else {
cout << max((a[1] + a[2]), (b[1] + b[2])) << endl;
}
}
return 0;
}
ABC 272 D Root M Leaper
题意:在一个N * N的矩阵中,你在(1, 1)处,每次可以通过移动到达其他的点,但是每次所达到的点距离上一点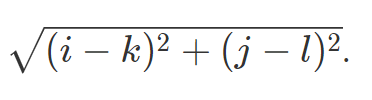
的距离,输出到达每个点最快是第几步,若无法到达则输出-1
思路:首先通过点(0, 0)计算出偏移量,然后直接进行一遍bfs即可
时间复杂度:O(n * n)
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 500;
int n, m;
int ans[N][N];
bool vis[N][N];
vector<PII> d;
void bfs(int x, int y) {
vis[x][y] = 1;
ans[x][y] = 0;
queue<PII> st;
st.push({x, y});
while (st.size()) {
auto p = st.front(); st.pop();
for (int i = 0; i < d.size(); i ++ ) {
int x = p.first + d[i].first, y = p.second + d[i].second;
if(x >= 1 && x <= n && y >= 1 && y <= n && !vis[x][y]) {
ans[x][y] = ans[p.first][p.second] + 1;
vis[x][y] = 1;
st.push({x, y});
}
}
}
}
int main() {
cin >> n >> m;
for (int i = 0; i <= n; i ++ ) {
for (int j = 0; j <= n; j ++ ) {
ans[i][j] = -1;
//计算偏移量
if(i * i + j * j == m) {
d.push_back({i, j});
d.push_back({i, -j});
d.push_back({-i, j});
d.push_back({-i, -j});
}
}
}
// for (auto i : d) {
// cout << i.first << " " << i.second << endl;
// }
bfs(1, 1);
for (int i = 1; i <= n; i ++ ) {
for (int j = 1; j <= n; j ++ ) {
cout << ans[i][j] << " ";
}
cout << endl;
}
return 0;
}
ABC 271 C Manga
题意:给予你个有n个数的数组,你可以使用数组中的两个数换成一个你想要的数,问从1开始最长你可以连续到多少
思路:二分查找,再给你个的数组中完成去重之后,通过二分查找可以得出,也可以通过模拟
时间复杂度:O(logn) (可能并不明确)
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 5;
int a[N];
int n, m;
bool check(int mid) {
int res = 0;
for (int i = 1; i <= m; i ++ ) {
res += (a[i] <= mid);
}
return (mid - res) * 2 <= (n - res);
}
int main() {
cin >> n;
for (int i = 1; i <= n; i ++ ) cin >> a[i];
sort(a + 1, a + 1 + n);
m = 1;
for (int i = 2; i <= n; i ++ ) {
if(a[i] != a[i - 1]) {
a[ ++ m] = a[i];
}
}
int l = 0, r = 1e9;
int ans = 0;
while (l < r) {
int mid = l + r + 1>> 1;
if(check(mid)) {
ans = mid;
l = mid;
}
else r = mid - 1;
}
cout << l << endl;
return 0;
}
ABC 271 D Flip and Adjust
题意:
有n个卡牌,每个卡牌的正反面都有数,你可以让其正面或者反面朝上,问是都有一个顺序可以使得所有朝上的卡牌的总值是S,若没有输出No,若存在输出Yes,并且输出顺序
思路:当时第一眼看到的就是使用dfs,但是n可以取到100,dfs就不行了(这里提醒一下,dfs最大也就是30,爆搜的时间复杂度是指数级别的),所以只能使用dp来解决,
dp (动态规划):
表示:dp[i][j]表示从前n个卡牌中选,总和正好是j的集合
属性:bool
状态转移式:
dp[i][j + a[i]] = dp[i - 1][j] (并且是dp[i - 1][j]状态存在的情况)
dp[i][j + b[i]] = dp[i - 1][j] (dp[i - 1][j]状态存在的情况)
判断dp[n][s]是都存在,若存在通过递归的方式得到摆放顺序
若不存在直接输出No
时间复杂度:O(n * 100000)
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10, M = N * 2;
int dp[110][N];
int a[N], b[N];
int n, s;
string ans;
void print(int u, int s) {
if(u == 0) return ;
if(dp[u - 1][s - a[u]]) {
print(u - 1, s - a[u]);
ans += 'H';
}
else {
print(u - 1, s - b[u]);
ans += 'T';
}
}
int main() {
cin >> n >> s;
for (int i = 1; i <= n; i ++ ) cin >> a[i] >> b[i];
//通过动态规划来确定存在状态
dp[0][0] = 1;
for (int i = 1; i <= n; i ++ ) {
for (int j = 0; j <= 10000; j ++ ) {
if(dp[i - 1][j]) {
dp[i][j + a[i]] = dp[i - 1][j];
dp[i][j + b[i]] = dp[i - 1][j];
}
}
}
cout << dp[n][s] << endl;
if(dp[n][s]) {
cout << "Yes" << endl;
print(n, s);
cout << ans << endl;
}
else {
cout << "No" << endl;
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号