【GZOI 2019】特技飞行
Problem
Description
公元 \(9012\) 年,Z 市的航空基地计划举行一场特技飞行表演。表演的场地可以看作一个二维平面直角坐标系,其中横坐标代表着水平位置,纵坐标代表着飞行高度。
在最初的计划中,这 \(n\) 架飞机首先会飞行到起点 \(x = x_{st}\) 处,其中第 \(i\) 架飞机在起点处的高度为 \(y_{i,0}\)。它们的目标是终点 \(x = x_{ed}\) 处,其中第 \(i\) 架飞机在终点处的高度应为 \(y_{i,1}\)。因此,每架飞机可以看作坐标系中的一个点,它的航线是从 \((x_{st},y_{i,0})\) 出发、到 \((x_{ed},y_{i,1})\) 结束的一条线段,如下图所示。
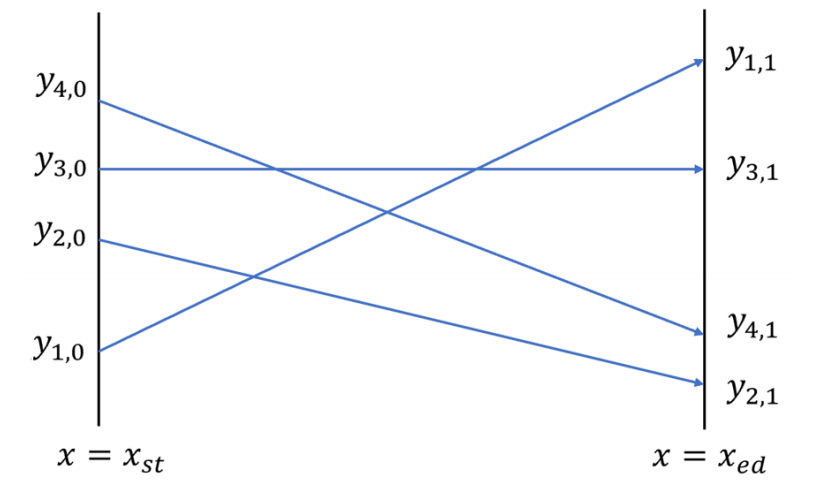
这 \(n\) 架飞机同时出发且始终保持一定的对地速度。因此,对于任意两条交叉的航线(线段),对应的两架飞机必然会同时到达交点处——这就是它们进行特技表演的时刻。它们将会偏转机翼,展现以极近的距离「擦身而过」特技,然后继续保持各自的航线。
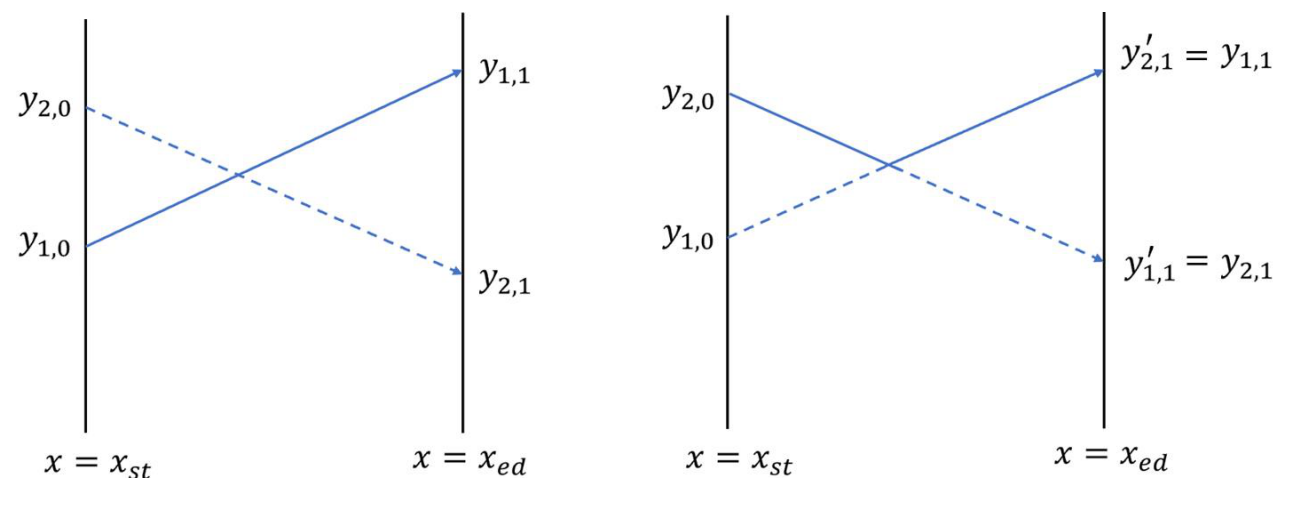
航空基地最近还研究了一种新的特技「对向交换」。当两架飞机到达交点处时,之前正在下降的那架立即转为执行抬升动作,之前正在上升的那架则执行一次空翻,两架飞机一上一下、机腹对机腹,同样以极近的距离经过交点,然后互相交换接下来的航线。
我们不必关心特技动作在物理上究竟是如何实现的,飞机仍然看作一个点,在两种特技动作下,航线的变化如下图所示(\(y_{i,1}'\) 表示交换航线后第 \(i\) 架飞机在终点的新高度)。容易发现,「对向交换」会使它们的航线变为折线,并保持它们在纵坐标上的相对顺序;而「擦身而过」会改变它们在纵坐标上的相对顺序。
现在,观看表演的嘉宾团提出了一个苛刻的要求——在终点 \(x = x_{ed}\) 处,按照高度排序,\(n\) 架飞机的相对顺序必须与 \(x = x_{st}\) 处的相对顺序一致。嘉宾团还给「对向交换」特技和「擦身而过」特技分别评定了难度系数 \(a\) 和 \(b\),每次「对向交换」特技可以获得 \(a\) 的分数,每次「擦身而过」特技可以获得 \(b\) 的分数。
除此以外,嘉宾团共有 \(k\) 名成员,第 \(i\) 名成员会乘热气球停留在位置 \((p_i,q_i)\) 处,具有 \(r_i\) 的观测距离,可以观测到区域 \(|x - p_i| + |y - q_i| \le r_i\) 里的所有特技。
若某个交点处的特技被一名或多名嘉宾观测到,则可以获得 \(c\) 的额外加分。
注意:特技无论是否被观测到,均可以获得 \(a\) 或者 \(b\) 的得分。
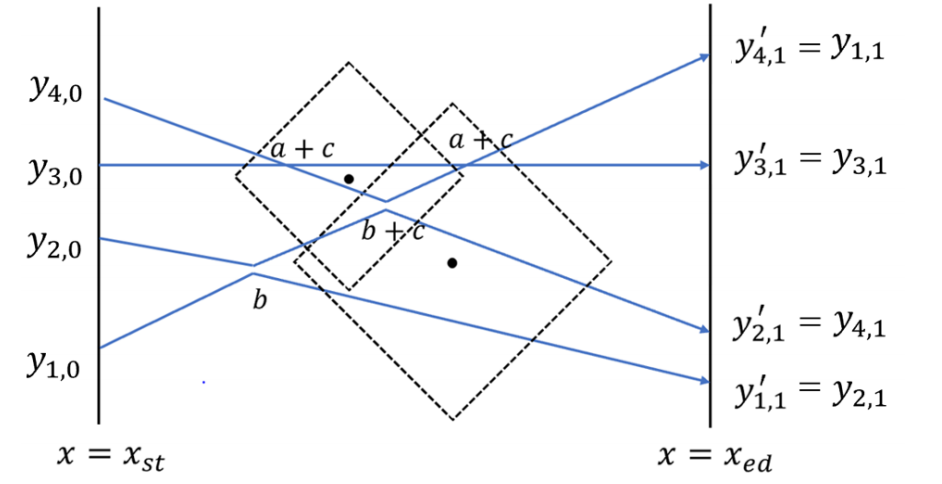
下图是对本题第一幅图 \(4\) 条航线 \(4\) 个交点的一种满足要求的安排,包括 \(2\) 次「对向交换」、\(2\) 次「擦身而过」,\(3\) 项特技被观测到,得分 \(2a + 2b + 3c\)。为了方便观察,图中展现「对向交换」特技的交点稍稍有些分离。
在这次的剧情里,你成为了 Z 市航空基地的规划员,你可以决定在每个交点处是执行「对向交换」还是「擦身而过」。你被要求在保证嘉宾团要求的前提下,计算整个特技表演的可能得到的最低和最高分数。
Input Format
第一行包含六个非负整数 \(n,a,b,c,x_{st},x_{ed}\),分别表示航线(线段)总数、「对向交换」特技的得分、「擦身而过」特技的得分、观测对表演的额外分、飞行起点的横坐标、飞行终点的横坐标。
第二行包含 \(n\) 个非负整数 \(y_{i,0}\),其中第 \(i\) 个数表示第 \(i\) 条航线起点的纵坐标,保证按照从低到高的顺序给出,即 \(y_{i,0} < y_{i + 1,0}\)。
第三行包含 \(n\) 个非负整数 \(y_{i,1}\),其中第 \(i\) 个数表示第 \(i\) 条航线终点的纵坐标。
第四行包含一个非负整数 \(k\),表示嘉宾的数量。
接下来 \(k\) 行每行三个非负整数 \(p_i,q_i,r_i\),分别表示第 \(i\) 名嘉宾所在位置的横、纵坐标与观测距离。
输入数据对于所有航线(线段)在直线 \(x = x_{st}\) 和 \(x = x_{ed}\) 之间的交点总数也有一些限制,详见「数据范围与提示」。
Output Format
输出只有一行,包含两个整数,表示整个特技飞行表演的可能得到的最低和最高分数,中间用一个空格隔开。
Sample
Input 1
4 1 2 3 1 6
1 2 3 4
4 1 3 2
2
3 3 1
5 2 2
Output 1
13 15
Input 2
10 73 28 13 0 100
2 9 16 25 29 34 43 46 52 58
8 25 35 52 41 5 16 3 19 48
5
46 40 1
37 27 5
67 34 1
65 28 4
29 38 1
Output 2
989 1619
Explainatioin for Input 1
该样例的航线就是题目描述的图中所画的情况,只是嘉宾所在的位置稍有不同。
最低得分的表演方案是在所有交点处均采用「对向交换」特技,得分 \(4a + 3c = 13\)。
最高得分的表演方案与题目描述的图中所画的情况一致,得分 \(2a + 2b + 3c = 15\)。
Range
不存在三条或三条以上的线段交于同一点。
所有坐标和 \(r_i\) 均为 \(5 \times 10^7\) 以内的非负整数。
\(y_{i,0} < y_{i + 1,0}\),\(y_{i,1}\) 各不相同。
\(x_{st} < p_i < x_{ed},1 ≤ a,b,c ≤ 10^3\)。
| 测试点编号 | \(n,k\) 的规模 | 交点数的规模 | 约定 |
|---|---|---|---|
| \(1\) | \(n,k \le 15\) | \(\le 40\) | 无 |
| \(2\) | \(n,k \le 15\) | \(\le 40\) | 无 |
| \(3\) | \(n,k \le 15\) | \(\le 40\) | 无 |
| \(4\) | \(n,k \le 15\) | \(\le 40\) | 无 |
| \(5\) | \(n \le 30.000,k \le 100\) | \(\le 200,000\) | 无 |
| \(6\) | \(n \le 30.000,k \le 100\) | \(\le 200,000\) | 无 |
| \(7\) | \(n \le 30.000,k \le 100\) | \(\le 200,000\) | 无 |
| \(8\) | \(n \le 30.000,k \le 100\) | \(\le 200,000\) | 无 |
| \(9\) | \(n,k \le 100,000\) | \(\le 500,000\) | \(a = b\) |
| \(10\) | \(n,k \le 100,000\) | \(\le 500,000\) | \(a = b\) |
| \(11\) | \(n,k \le 100,000\) | \(\le 500,000\) | \(a = b\) |
| \(12\) | \(n,k \le 100,000\) | \(\le 500,000\) | \(a = b\) |
| \(13\) | \(n,k \le 50,000\) | \(\le 250,000\) | 无 |
| \(14\) | \(n,k \le 50,000\) | \(\le 250,000\) | 无 |
| \(15\) | \(n,k \le 50,000\) | \(\le 250,000\) | 无 |
| \(16\) | \(n,k \le 50,000\) | \(\le 250,000\) | 无 |
| \(17\) | \(n,k \le 100,000\) | \(\le 500,000\) | 无 |
| \(18\) | \(n,k \le 100,000\) | \(\le 500,000\) | 无 |
| \(19\) | \(n,k \le 100,000\) | \(\le 500,000\) | 无 |
| \(20\) | \(n,k \le 100,000\) | \(\le 500,000\) | 无 |
Algorithm
向量,扫描线
Mentality
考场上打的全是麻烦的算法 .jpg 。
\(step1:\)
首先发现,由于交点数不多,显然先求交点。对于两条线段,它们相交当且仅当左端点纵坐标的大小关系和右端点相反。
由于题目按照左端点纵坐标单调递增给出,直接用一个 \(set\) 维护已给出的右端点纵坐标集合,对于新线段暴力扫一遍 \(set\) 中的线段,看是否相交。
求交点其实很简单,利用斜率就好了。
奈何我选择了叉积 \((???)\),我也觉得自己挺迷的。
\(step2:\)
对于每个嘉宾,直接将嘉宾和交点坐标转换成切比雪夫意义下的坐标,二维数点即可。
这里使用扫描线二维数点。
\(step3:\)
接下来剩下的是翻折操作。
不难发现,由于 \(a,b\) 有明确的大小关系,所以两个极端答案肯定是尽量多选 \(a\) 和尽量少选 \(a\) 。
对于尽量多选 \(a\) ,也就是翻折操作,我们发现其实可以所有操作全部翻折,最后到右边之后,一定会是有序的。
这个有两种理解方式:
一、交点数等价于逆序对数,一次翻折就相当于扭回去了一对逆序对,当我们将所有逆序对都扭回去之后,序列不存在逆序对,即结果有序。
二、题面中有提到:一次翻折操作会使两架飞机仍保持相对位置不变。那么我们每次都进行翻折,始终不会有任意两架飞机交换位置,所以最后结果有序。
对于尽量少选 \(a\) ,我们将每个飞机 \(i\) 和它的目的地 \(p_i\) 相连,就会得到一张只存在简单环的图。
不难发现,对于一个环,设其中元素分别为 \(a_1\sim a_n\) 它的形式如下:
\(\forall_{i=1}^{n-1}p_{a_i}=a_{i+1}\)
\(p_{a_n}=a_1\)
由于交换元素仅针对逆序对,所以要将环整体位移一位最少也就需要环长减一的次数。
所以 \(a\) 的最少选择次数为所有环的环长减一之和。
没了。
Code
考场的时候脑子比较乱,代码也就打得长了。我也不知道我为什么码出了 \(5k\)
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <iostream>
#include <set>
using namespace std;
#define LL long long
#define go(x, i, v) for (int i = hd[x], v = to[i]; i; v = to[i = nx[i]])
#define inline __inline__ __attribute__((always_inline))
inline LL read() {
LL x = 0, w = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') w = -1;
ch = getchar();
}
while (isdigit(ch)) {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar();
}
return x * w;
}
const int Max_n = 1e5 + 5;
int n, a, b, c, K, ans;
int cnt, cc;
LL Ans1, Ans2;
double xs, xe, ys[Max_n], ye[Max_n];
struct dots {
double x, y;
} k[Max_n * 5];
struct xl {
double x, y;
double operator*(const xl &b) { return x * b.y - b.x * y; }
};
set<pair<double, double> > s;
set<pair<double, double> >::iterator it;
inline bool cmp(dots a, dots b) { return a.x == b.x ? a.y < b.y : a.x < b.x; }
inline void part1() {
n = read(), a = read(), b = read(), c = read(), xs = read(), xe = read();
for (int i = 1; i <= n; i++) ys[i] = read();
double D = xe - xs;
for (int i = 1; i <= n; i++) {
ye[i] = read();
it = s.end();
if (s.size()) it--;
while ((*it).first > ye[i] && it != s.begin()) {
cnt++;
xl d1 = (xl){-D, ys[i] - (*it).first}, d2 = (xl){0, ye[i] - (*it).first};
double S1 = abs(d1 * d2);
d1 = (xl){D, ye[i] - (*it).second}, d2 = (xl){0, ys[i] - (*it).second};
double S2 = abs(d1 * d2);
double K = S2 / (S1 + S2), D1 = (*it).first - (*it).second;
k[cnt].x = xs + D * K, k[cnt].y = (*it).second + K * D1;
it--;
}
if (it == s.begin())
if ((*it).first > ye[i]) {
cnt++;
xl d1 = (xl){-D, ys[i] - (*it).first},
d2 = (xl){0, ye[i] - (*it).first};
double S1 = abs(d1 * d2);
d1 = (xl){D, ye[i] - (*it).second}, d2 = (xl){0, ys[i] - (*it).second};
double S2 = abs(d1 * d2);
double K = S2 / (S1 + S2), D1 = (*it).first - (*it).second;
k[cnt].x = xs + D * K, k[cnt].y = (*it).second + K * D1;
}
s.insert(make_pair(ye[i], ys[i]));
}
for (int i = 1; i <= cnt; i++) {
double X = k[i].x, Y = k[i].y;
k[i].x = X + Y, k[i].y = X - Y;
}
sort(k + 1, k + cnt + 1, cmp);
}
double z[Max_n << 4];
int C[Max_n << 3];
int cntr, hd[Max_n], nx[Max_n << 1], to[Max_n << 1];
struct que {
double pos;
double l, r, L, R;
int id, t;
} q[Max_n << 3];
struct person {
double x, y, r;
} p[Max_n];
inline bool cmp2(que a, que b) {
return a.pos == b.pos ? a.t < b.t : a.pos < b.pos;
}
inline void add(int k, int x) {
for (int i = k; i <= cc; i += i & -i) C[i] += x;
}
inline int query(int k) {
int ans = 0;
for (int i = k; i; i -= i & -i) ans += C[i];
return ans;
}
inline void part2() {
K = read();
for (int i = 1; i <= K; i++) {
p[i].x = read(), p[i].y = read(), p[i].r = read();
double X = p[i].x, Y = p[i].y;
p[i].x = X + Y, p[i].y = X - Y;
}
int Cnt = 0;
for (int i = 1; i <= K; i++) {
Cnt++;
q[Cnt].l = p[i].x - p[i].r, q[Cnt].r = p[i].x + p[i].r;
q[Cnt].L = p[i].y - p[i].r, q[Cnt].R = p[i].y + p[i].r;
q[Cnt].t = 1, q[Cnt + 1] = q[Cnt], q[Cnt + 1].t = 3;
q[Cnt].pos = q[Cnt].l, q[++Cnt].pos = q[Cnt].r;
z[++cc] = q[Cnt].L, z[++cc] = q[Cnt].R;
q[Cnt].id = q[Cnt - 1].id = i;
}
for (int i = 1; i <= cnt; i++) {
Cnt++, q[Cnt].pos = k[i].x, q[Cnt].l = k[i].y, q[Cnt].t = 2;
z[++cc] = q[Cnt].l;
}
sort(q + 1, q + Cnt + 1, cmp2);
sort(z + 1, z + cc + 1);
for (int i = 1; i <= Cnt; i++) {
if (q[i].t == 1) {
int x = lower_bound(z + 1, z + cc + 1, q[i].R) - z;
int y = lower_bound(z + 1, z + cc + 1, q[i].L) - z;
add(y, 1), add(x + 1, -1);
}
if (q[i].t == 3) {
int x = lower_bound(z + 1, z + cc + 1, q[i].R) - z;
int y = lower_bound(z + 1, z + cc + 1, q[i].L) - z;
add(y, -1), add(x + 1, 1);
}
if (q[i].t == 2) {
int x = lower_bound(z + 1, z + cc + 1, q[i].l) - z;
if (query(x)) ans++;
}
}
Ans1 += 1ll * ans * c, Ans2 += 1ll * ans * c;
Ans1 += 1ll * a * cnt;
}
int num[Max_n], P[Max_n];
int top, tim, dfn[Max_n], low[Max_n], vis[Max_n], stk[Max_n];
int size[Max_n], bel[Max_n], cir;
bool cmp3(int a, int b) { return ye[a] < ye[b]; }
void addr(int u, int v) {
cntr++;
nx[cntr] = hd[u], to[cntr] = v;
hd[u] = cntr;
}
void dfs(int x) {
stk[++top] = x, dfn[x] = low[x] = ++tim, vis[x] = 1;
go(x, i, v) if (!vis[v]) dfs(v), low[x] = min(low[x], low[v]);
else if (vis[v] == 1) low[x] = min(low[x], dfn[v]);
if (dfn[x] == low[x]) {
cir++;
while (stk[top] != x)
bel[stk[top]] = cir, size[cir]++, vis[stk[top--]] = -1;
top--, bel[x] = cir, size[cir]++;
}
}
void part3() {
for (int i = 1; i <= n; i++) num[i] = i;
sort(num + 1, num + n + 1, cmp3);
for (int i = 1; i <= n; i++) addr(num[i], i), addr(i, num[i]);
for (int i = 1; i <= n; i++)
if (!dfn[i]) dfs(i);
int tot = 0;
for (int i = 1; i <= cir; i++) tot += size[i] - 1;
Ans2 += 1ll * tot * a + 1ll * (cnt - tot) * b;
}
int main() {
#ifndef ONLINE_JUDGE
freopen("trick.in", "r", stdin);
freopen("trick.out", "w", stdout);
#endif
part1();
part2();
part3();
if (Ans1 > Ans2) swap(Ans1, Ans2);
cout << Ans1 << " " << Ans2;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号