数学选做
LCMSUM - LCM Sum
\(\begin{aligned}
ans_n&=\sum\limits_{i=1}^n\operatorname{lcm}(i,n)\\
&=\sum\limits_{i=1}^n\frac{i\times n}{\gcd(i,n)}\\
&=n\sum\limits_{i=1}^n\frac{i}{gcd(i,n)}\\
&=n\sum\limits_{d\mid n}\sum\limits_{i=1}^n\frac{i}{d}\left[\gcd(i,n)=d\right]\\
&=n\sum\limits_{d\mid n}\sum\limits_{i=1}^{\frac{n}{d}} i\left[\gcd(i,\frac{n}{d})=1\right]\\
&=n\sum\limits_{d\mid n}\sum\limits_{i=1}^di\left[\gcd(i,d)=1\right]\\
&=n+n\sum\limits_{d\mid n\text{且} d\not=1}\frac{\phi(d)\times d}{2}
\end{aligned}\)
因为当 \(d>1\) 时,若 \(a\perp d\),则 \((d-a)\perp d\),所以与 \(d\) 互质的数必然会两两成对,且和为 \(d\),这样的对数为 \(\frac{\phi(d)}{2}\)。所以当 \(d>1\) 时,\(\sum\limits_{i=1}^di\left[gcd(i,d)=1\right]=\frac{\phi(d)\times d}{2}\)。
预处理出所有 \(n\) 的答案即可。
点击查看代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define int long long
#define pdi pair<double,int>
#define pii pair<int,int>
#define pb push_back
#define mp make_pair
#define eps 1e-9
using namespace std;
namespace IO{
template<typename T>
inline void read(T &x){
x=0;
int f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-'){
f=-1;
}
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
x=(f==1?x:-x);
}
template<typename T>
inline void write(T x){
if(x<0){
putchar('-');
x=-x;
}
if(x>=10){
write(x/10);
}
putchar(x%10+'0');
}
template<typename T>
inline void write_endl(T x){
write(x);
putchar('\n');
}
template<typename T>
inline void write_space(T x){
write(x);
putchar(' ');
}
}
using namespace IO;
const int N=1e6+10;
int phi[N],ans[N],prime[N],cnt;
void init(int mx){
for(int i=2;i<=mx;i++){
if(!phi[i]){
prime[++cnt]=i;
phi[i]=i-1;
}
for(int j=1;j<=cnt&&prime[j]*i<=mx;j++){
if(i%prime[j]==0){
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
phi[i*prime[j]]=phi[i]*phi[prime[j]];
}
}
}
void get_ans(int mx){
for(int i=1;i<=mx;i++){
for(int j=1;i*j<=mx;j++){
ans[i*j]+=phi[i]*i/2;
}
}
for(int i=1;i<=mx;i++){
ans[i]=ans[i]*i;
}
for(int i=1;i<=mx;i++){
ans[i]+=i;
}
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
init(1e6);
get_ans(1e6);
int t;
read(t);
while(t--){
int n;
read(n);
write_endl(ans[n]);
}
return 0;
}
[国家集训队]Crash的数字表格 / JZPTAB
令 \(n<m\)
枚举 \(\gcd\)
令 \(i=\frac{i}{d},j=\lfloor\frac{j}{d}\rfloor\)
根据莫比乌斯函数的性质,若 \(\gcd(i,j)=1\),则 \(\sum\limits_{t\mid \gcd(i,j)}\mu(t)\) 为 \(1\),否则为 \(0\)。转化得:
转化一下
令 \(i=\frac{i}{t},j=\frac{j}{t}\)
令 \(T=dt\)
令 \(s(x)\) 表示 \(\sum\limits_{i=1}^x i,f(x)=\sum\limits_{y\mid x}\mu(x)x\)
因为 \(\mu(x)\) 和 \(x\) 均为积性函数,所以 \(\mu(x)x\) 是积性函数,他与 \(1\) 狄利克雷卷积后的函数也是积性函数,即 \(f(x)\) 为积性函数,可以通过线性筛预处理得到,\(s(x)=\frac{x(x+1)}{2}\),可以直接算。最后按照式子算下去即可(也可以使用整除分块)。
点击查看代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define int long long
#define pdi pair<double,int>
#define pii pair<int,int>
#define pb push_back
#define mp make_pair
#define eps 1e-9
using namespace std;
namespace IO{
template<typename T>
inline void read(T &x){
x=0;
int f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-'){
f=-1;
}
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
x=(f==1?x:-x);
}
template<typename T>
inline void write(T x){
if(x<0){
putchar('-');
x=-x;
}
if(x>=10){
write(x/10);
}
putchar(x%10+'0');
}
template<typename T>
inline void write_endl(T x){
write(x);
putchar('\n');
}
template<typename T>
inline void write_space(T x){
write(x);
putchar(' ');
}
}
using namespace IO;
const int N=1e7+10,mod=20101009;
int f[N],prime[N],is_prime[N],s[N],sum[N],cnt;
void init(int mx){
f[1]=1;
for(int i=2;i<=mx;i++){
if(!is_prime[i]){
f[i]=(1-i+mod)%mod;
prime[++cnt]=i;
}
for(int j=1;j<=cnt&&i*prime[j]<=mx;j++){
is_prime[i*prime[j]]=1;
if(i%prime[j]==0){
f[i*prime[j]]=f[i];
break;
}
f[i*prime[j]]=f[i]*f[prime[j]]%mod;
}
}
for(int i=1;i<=mx;i++){
sum[i]=(sum[i-1]+f[i]*i%mod)%mod;
s[i]=(s[i-1]+i)%mod;
}
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
init(1e7);
int n,m;
read(n),read(m);
if(n>m){
swap(n,m);
}
int ans=0;
for(int i=1,j;i<=n;i++){
ans=(ans+(f[i]+mod)%mod*i%mod*s[n/i]%mod*s[m/i]%mod)%mod;
}
write_endl(ans);
return 0;
}
[HAOI2011]Problem b
令 \(f(n,m)\) 表示 \(\sum\limits_{i=1}^n\sum\limits_{j=1}^m\left[gcd(i,j)=k\right]\)
令 \(i=\frac{i}{d},j=\frac{j}{d}\)
根据莫反性质得
因为 \(d\mid \gcd(i,j),\gcd(i,j)\mid i,\gcd(i,j)\mid j\),所以枚举 \(d\) 后满足条件的 \((i,j)\) 有 \(\lfloor\frac{n}{dk}\rfloor\lfloor\frac{m}{dk}\rfloor\) 对。最后像二维前缀和一样,\(ans=f(b,d)-f(b,c-1)-f(a-1,d)+f(a-1,c-1)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e4+10;
bool isprime[maxn];
int prime[maxn],mu[maxn],sum[maxn],cnt,n,a,b,c,d,k;
void init(int n){
mu[1]=1;
for(int i=2;i<=n;i++){
if(!isprime[i]){
prime[++cnt]=i;
mu[i]=-1;
}
for(int j=1;j<=cnt;j++){
if(i*prime[j]>n)break;
isprime[i*prime[j]]=1;
if(i%prime[j]==0){
break;
}
mu[i*prime[j]]=-mu[i];
}
}
for(int i=1;i<=n;i++){
sum[i]=sum[i-1]+mu[i];
}
}
int solve(int a,int b){
static int mn;
static int ans;
mn=min(a,b);
ans=0;
for(int l=1,r;l<=mn;l=r+1){
r=min(a/(a/l),b/(b/l));
ans+=(a/(k*l))*(b/(k*l))*(sum[r]-sum[l-1]);
}
return ans;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
init(50000);
cin>>n;
while(n--){
cin>>a>>b>>c>>d>>k;
cout<<solve(b,d)-solve(b,c-1)-solve(a-1,d)+solve(a-1,c-1)<<endl;
}
return 0;
}
[AGC019F] Yes or No
组合意义的巧妙运用
容易发现选择剩余多的答案的正确概率更高,所以最优策略肯定是优先选择剩余多的答案,如果两个答案数量相同,随意选。
可以将这个操作转到网格图上(这里借用一下粉兔的图)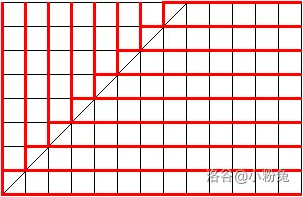
令 \(n>m\),横着的表示 YES 的个数,竖着的表示 NO 的个数,红色的线段表示回答正确的,答案相当于从 \((n,m)\) 走到 \((1,1)\) 时期望经过多少红色的线段。先忽略斜线上向左走的线段,那么斜线上方的部分可以通过翻折到达斜线下方,所以最少会回答对 \(n\) 道题。
再考虑斜线上的点,因为 \(n=m\),所以无论选什么正确率均为 \(50\%\)。考虑所有经过点 \((i,i)\) 的路径,边 \((i,i)\rightarrow(i,i-1)\) 和边 \((i,i)\rightarrow(i-1,i)\) 各有 \(50\%\) 的概率被染色,产生 \(1\) 的贡献。所以总答案为 \(n+\frac{1}{2}\sum\limits_{i=1}^m\frac{\binom{2i}{i}\binom{n+m-2i}{n-i}}{\binom{n+m}{m}}\)
点击查看代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define int long long
#define pdi pair<double,int>
#define pii pair<int,int>
#define pb push_back
#define mp make_pair
#define eps 1e-9
using namespace std;
namespace IO{
template<typename T>
inline void read(T &x){
x=0;
int f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-'){
f=-1;
}
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
x=(f==1?x:-x);
}
template<typename T>
inline void write(T x){
if(x<0){
putchar('-');
x=-x;
}
if(x>=10){
write(x/10);
}
putchar(x%10+'0');
}
template<typename T>
inline void write_endl(T x){
write(x);
putchar('\n');
}
template<typename T>
inline void write_space(T x){
write(x);
putchar(' ');
}
}
using namespace IO;
const int N=1e6+10,mod=998244353;
int n,m,fac[N],inv[N];
int qpow(int a,int b){
int res=1;
while(b){
if(b&1){
res=res*a%mod;
}
a=a*a%mod;
b>>=1;
}
return res;
}
void init(int mx){
fac[0]=1;
for(int i=1;i<=mx;i++){
fac[i]=fac[i-1]*i%mod;
}
inv[mx]=qpow(fac[mx],mod-2);
for(int i=mx-1;i>=0;i--){
inv[i]=inv[i+1]*(i+1)%mod;
}
}
int C(int n,int m){
return fac[n]*inv[n-m]%mod*inv[m]%mod;
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
init(1e6);
read(n),read(m);
if(n<m){
swap(n,m);
}
int ans=0;
for(int i=1;i<=m;i++){
ans=(ans+C(2*i,i)*C(n+m-2*i,m-i)%mod*qpow(C(n+m,n),mod-2)%mod)%mod;
}
write_endl((ans*qpow(2,mod-2)+n)%mod);
return 0;
}
[ABC205E] White and Black Balls
令 \(f_{i,j}\) 表示 \(i\) 个白球 \(j\) 个黑球的合法方案数。\(f_{i,j}=f_{i,j-1}+f_{i-1,j}\times [i\le j+k]\),这是 \(O(n^2)\) 的考虑优化。可以发现这个很像组合数学的式子。将它放到网格图上,可以发现它就是从 \((0,0)\) 到 \((n,m)\),且不穿过过直线 \(y=x+k\),即碰到 \(y=x+k+1\) 是不合法的。将 \((0,0)\) 延直线 \(y=x+k+1\) 对称过去,从 \((-k-1,k+1)\) 到 \((n,m)\) 的路径必然非法,答案为 \(\max(0,\dbinom{n+m}{m}-\dbinom{n+m}{m+k+1})\)。
点击查看代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define int long long
#define pdi pair<double,int>
#define pii pair<int,int>
#define pb push_back
#define mp make_pair
#define eps 1e-9
using namespace std;
namespace IO{
template<typename T>
inline void read(T &x){
x=0;
int f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-'){
f=-1;
}
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
x=(f==1?x:-x);
}
template<typename T>
inline void write(T x){
if(x<0){
putchar('-');
x=-x;
}
if(x>=10){
write(x/10);
}
putchar(x%10+'0');
}
template<typename T>
inline void write_endl(T x){
write(x);
putchar('\n');
}
template<typename T>
inline void write_space(T x){
write(x);
putchar(' ');
}
}
using namespace IO;
const int N=2e6,mod=1e9+7;
int n,m,k,fac[N+10],inv[N+10];
int qpow(int a,int b){
int res=1;
while(b){
if(b&1){
res=res*a%mod;
}
a=a*a%mod;
b>>=1;
}
return res;
}
int C(int n,int m){
if(m>n||m<0||n<0){
return 0;
}
return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
read(n),read(m),read(k);
inv[0]=fac[0]=1;
for(int i=1;i<=N;i++){
fac[i]=fac[i-1]*i%mod;
}
inv[N]=qpow(fac[N],mod-2);
for(int i=N-1;i>=0;i--){
inv[i]=inv[i+1]*(i+1)%mod;
}
if(min(n,m)<min(n-k-1,m+k+1)){
write_endl(0);
}
else{
write_endl((C(n+m,n)-C(n+m,m+k+1)+mod)%mod);
}
return 0;
}
Koishi Loves Construction
一道不错的数学题。
对于Task1,\(n\) 肯定是要放在第一个的,不然 \(s_{i-1}+n\equiv s_i\pmod n\)。因为 \(s_n=\frac{n(n+1)}{2}\),当 \(2\nmid n\) 时,\(s_n\equiv s_1\pmod n\),这是无解的。对于剩下的 \(n\),可以尝试构造一个 \(\mod n\) 为 \(0,1,n-1,2,n-2,\dots,\frac{n}{2}+1,\frac{n}{2}\) 的 \(s\) 数组,那么得到 \(a_i=\begin{cases}n-i+1&2\mid i\\i-1&2\nmid i\end{cases}\)。
对于Task2,\(1\) 肯定是放在第一个,\(n\) 肯定放在最后一个,不然 \(s_{i-1}\times 1\equiv s_i\pmod n,s_{i-1}\times n\equiv 0\pmod n,0\times a_i\equiv 0\pmod n\)。上述的式子启示我们不能凑出 \(0\),显然对于任何一个合数,必然存在 \(1<p,q<n\text{且}p\not=q,p\times q\equiv 0\pmod n\)。所以合数肯定是无解,但 \(4\) 例外,因为 \(4=2\times 2\),可以构造出 \(1 3 2 4\) 满足条件。对于质数,可以尝试构造 \(\mod n\) 为 \(1,2,3,\dots,n\) 的 \(s\) 序列,即对于 \(\forall 1<i<n\),\(a_i\equiv \frac{i}{i-1}\pmod n\),因为 \(n\) 是质数,所以是可以满足的。
虽然带点分类讨论,但总体来说这个数学题还是不错的。
点击查看代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define int long long
#define pdi pair<double,int>
#define pii pair<int,int>
#define pb push_back
#define mp make_pair
#define eps 1e-9
using namespace std;
namespace IO{
template<typename T>
inline void read(T &x){
x=0;
int f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-'){
f=-1;
}
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
x=(f==1?x:-x);
}
template<typename T>
inline void write(T x){
if(x<0){
putchar('-');
x=-x;
}
if(x>=10){
write(x/10);
}
putchar(x%10+'0');
}
template<typename T>
inline void write_endl(T x){
write(x);
putchar('\n');
}
template<typename T>
inline void write_space(T x){
write(x);
putchar(' ');
}
}
using namespace IO;
void solve1(int n){
if(n==1){
puts("2 1");
return;
}
if(n%2){
puts("0");
return;
}
write_space(2);
for(int i=1;i<=n;i++){
if(i%2){
write_space(n-i+1);
}
else{
write_space(i-1);
}
}
putchar('\n');
}
bool check_prime(int x){
if(x<4){
return 1;
}
for(int i=2;i*i<=x;i++){
if(x%i==0){
return 0;
}
}
return 1;
}
int qpow(int a,int b,int mod){
int res=1;
while(b){
if(b%2){
res=res*a%mod;
}
b>>=1;
a=a*a%mod;
}
return res;
}
void solve2(int n){
if(check_prime(n)){
write_space(2),write_space(1);
for(int i=2;i<n;i++){
write_space(i*qpow(i-1,n-2,n)%n);
}
write_endl(n);
return;
}
if(n==4){
puts("2 1 3 2 4");
return;
}
puts("0");
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
int opt,t;
read(opt),read(t);
while(t--){
int n;
read(n);
if(opt==1){
solve1(n);
}
else{
solve2(n);
}
}
return 0;
}
Make It One
ZZQ 和 xc 两人duel的题,最后xc花了一晚上将其拿下,质量还可以。
容易发现的是 \(2\times 3\times 5\times 7\times 11\times 13\times 17=510510>300000\),因为选的是子集,所以答案不会超过 \(7\)。\(7\) 就是一大常数,不足畏惧,所以我们考虑枚举答案,判断答案的可行性即可。
判断答案是否可行肯定不能枚举集合是吧,一般这种判断是否可行的题,我们会使用可行性dp,令 \(f_i\) 表示 \(\gcd\) 是否能为 \(i\),发现这样不好转移,于是将 dp 状态转移改为 \(\gcd\) 为 \(i\) 的方案数。可以发现 \(f\) 依然不是很好转移,但我们可以像二项式反演一样,令 \(g_i\) 表示 \(\gcd\) 为 \(i\) 的倍数的方案数,这个是好算的 \(g_i=\binom{cnt_i}{ans}\),其中 \(cnt_i\) 表示有多少个 \(i\) 的倍数的数同时 \(g_i=\sum\limits_{i\mid j}f_j\),将式子变化一下可得 \(f_i=g_i-\sum\limits_{j=2}^{\lfloor\frac{n}{i}\rfloor}f_{ij}\),从大往小做即可。
点击查看代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define pii pair<int,int>
#define pdi pair<double,int>
#define pb push_back
#define eps 1e-9
#define mp make_pair
using namespace std;
namespace IO{
template<typename T>
inline void read(T &x){
x=0;
int f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-'){
f=-1;
}
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
x=(f==1?x:-x);
}
template<typename T>
inline void write(T x){
if(x<0){
putchar('-');
x=-x;
}
if(x>=10){
write(x/10);
}
putchar(x%10+'0');
}
template<typename T>
inline void write_endl(T x){
write(x);
putchar('\n');
}
template<typename T>
inline void write_space(T x){
write(x);
putchar(' ');
}
}
using namespace IO;
const int N=3e5+10,mod=1e9+7;
int n,a[N],cnt[N],fac[N],inv[N],f[N],MX;
int qpow(int a,int b){
int res=1;
while(b){
if(b&1){
res=1ll*res*a%mod;
}
a=1ll*a*a%mod;
b>>=1;
}
return res;
}
void init(int mx){
fac[0]=1;
for(int i=1;i<=mx;i++){
fac[i]=1ll*fac[i-1]*i%mod;
}
inv[mx]=qpow(fac[mx],mod-2);
for(int i=mx-1;i>=0;i--){
inv[i]=1ll*inv[i+1]*(i+1)%mod;
}
}
int C(int n,int m){
return 1ll*fac[n]*inv[n-m]%mod*inv[m]%mod;
}
int work(int x){
for(int i=MX;i;i--){
f[i]=C(cnt[i],x);
for(int j=i*2;j<=MX;j+=i){
f[i]=(f[i]-f[j]+mod)%mod;
}
}
return f[1];
}
void solve(){
read(n);
init(3e5);
for(int i=1;i<=n;i++){
read(a[i]);
if(a[i]==1){
puts("1");
return;
}
cnt[a[i]]++;
MX=max(MX,a[i]);
}
for(int i=1;i<=MX;i++){
for(int j=i*2;j<=MX;j+=i){
cnt[i]+=cnt[j];
}
}
for(int i=2;i<=7;i++){
if(work(i)){
write_endl(i);
return;
}
}
puts("-1");
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
int t=1;
while(t--){
solve();
}
return 0;
}
Almost Perfect
先考虑一个排列的逆排列是什么,考虑将 \(p_i=j\) 表示为连一条从 \(i\) 到 \(j\) 的边,那么一个排列的逆排列就相当于将所有边都取反。基于这个,所有大小为 \(1\) 和大小为 \(2\) 的环都是可行的。那么还有更大的环可行吗?
对于大小为 \(3\) 的环,假设其三个点按照顺序分别为 \(b,c,a\),即存在边 \(a\rightarrow b,b\rightarrow c,c\rightarrow a\),那么逆排列对应的环为 \(c,a,b\)。根据定义可以得到 \(|b-c|\le 1,|a-c|\le 1,|a-b|\le 1\),显然不同的三个数是不可能满足这个条件的。
对于大小为 \(4\) 的环,假设其为 \(b,c,d,a\),逆排列对应的环为 \(d,a,b,c\)。可以得到 \(|c-a|\le 1,|d-b|\le 1\)。分类讨论一下,有 \(c>a,d>b;c>a,b>d;a>c,d>b;a>c,b>d\) 四种,但因为环可以旋转,将环旋转 \(180\text{°}\) 后可以得到第 \(1\) 种和第 \(4\) 中等价,第 \(2\) 种和第 \(3\) 种等价,所以只有两种不重的合法环。
归纳一下刚才的分析,可以发现环上任意两个距离为 \(2\) 的点都要求满足上述条件,在被要求满足条件的点对中连条边,可以发现会形成 \(1\sim 2\) 个连通块,至少会有一个连通块中有至少 \(3\) 个点,连续 \(n(n>2)\) 个自然数的极差一定大于 \(1\)。因此合法情况只有上述四种。
先将大小为 \(4\) 的环抛开,只考虑环的大小为 \(1\) 或 \(2\)。因为只有一种选法,所以可以直接dp,令 \(f_i\) 表示只包含大小为 \(1\) 或 \(2\) 的环的方案数。考虑大小为 \(4\) 的环怎么做,考虑将 \(i+1\) 和 \(i\) 绑定,假定选择 \(k\) 个大小为 \(4\) 的环。相当于将剩下的 \(n-4k\) 个点放在 \(2k\) 个点隔出来的的 \(2k+1\) 个间隔中(第一个点左侧可放,第 \(2k\) 个点右侧可放),根据插板法,共有 \(\binom{n-2k}{2k}\) 种选法。将所有的点随机排列,相邻的两个点组成一组,这个大小为 \(4\) 的环里面有为 \(i,j,i+1,j+1\),注意到这个是有序的,因为总共 \(i,j\) 位置不同,能组出两种不同的大小为 \(4\) 的环,共有 \((2k)!\) 种排法,但有重复,所以再除掉 \(k\) 个组自由排列的 \(k!\) 种排法。所以总答案为 \(\sum\limits_{k=1}^{\lfloor\frac{n}{4}\rfloor}\binom{n-2k}{2k}\frac{2k!}{k!}f_{n-4k}\)。
点击查看代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define pii pair<int,int>
#define pdi pair<double,int>
#define pb push_back
#define eps 1e-9
#define mp make_pair
using namespace std;
namespace IO{
template<typename T>
inline void read(T &x){
x=0;
int f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-'){
f=-1;
}
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
x=(f==1?x:-x);
}
template<typename T>
inline void write(T x){
if(x<0){
putchar('-');
x=-x;
}
if(x>=10){
write(x/10);
}
putchar(x%10+'0');
}
template<typename T>
inline void write_endl(T x){
write(x);
putchar('\n');
}
template<typename T>
inline void write_space(T x){
write(x);
putchar(' ');
}
}
using namespace IO;
const int N=3e5+10,mod=998244353;
int f[N],fac[N],inv[N];
int qpow(int a,int b){
int res=1;
while(b){
if(b&1){
res=1ll*res*a%mod;
}
a=1ll*a*a%mod;
b>>=1;
}
return res;
}
int C(int n,int m){
return 1ll*fac[n]*inv[m]%mod*inv[n-m]%mod;
}
void init(int mx){
f[1]=f[0]=1;
for(int i=2;i<=mx;i++){
f[i]=(f[i-1]+1ll*f[i-2]*(i-1)%mod)%mod;
}
fac[0]=1;
for(int i=1;i<=mx;i++){
fac[i]=1ll*fac[i-1]*i%mod;
}
inv[mx]=qpow(fac[mx],mod-2);
for(int i=mx-1;i>=0;i--){
inv[i]=1ll*inv[i+1]*(i+1)%mod;
}
}
void solve(){
int n;
read(n);
int ans=0;
for(int i=0;i*4<=n;i++){
ans=(ans+1ll*C(n-2*i,i*2)*fac[i*2]%mod*inv[i]%mod*f[n-4*i]%mod)%mod;
}
write_endl(ans);
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
init(3e5);
int t;
read(t);
while(t--){
solve();
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号