小白1-G铺垫（1-7需要dp所以先学了一下dp的）

原文

http://www.360doc.com/content/13/0601/00/8076359_289597587.shtml

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 然后就是这篇文章有点问题 换了另外一篇

 

—————————————————————————————————————————————————————

https://blog.csdn.net/qq_23826663/article/details/77581250

为CSDN博主「qq_23826663」的原创文章

 

以6 , 4 , 5 , 8 , 7 , 3 , 9为例，最长非降子序列为{4，5 , 8 , 9}和{4，5 , 7 , 9}，相应的其长度为4。
解题思路：
因为子序列的定义并不要求元素是数组中连续的数，我们也不得而知最长子序列将从哪一个地方开始，所以不能像连续子序列那样用遍历的方式去找到最长子序列的开始位置和结束位置。那么我们能考虑的就是针对数组中每一个元素去确定：当数组游标从开头走到某元素时，以该元素结尾的最长非降子序列的长度是多少。这样我们比较以每一个数组元素结尾的非降子序列的长度就可以得到最大长度。
1
解题过程：
声明一个与原数组arr长度一样的数组num, num[i]表示以arr[i]结尾的最长非降子序列的长度
分析得到动态规划的递推式
(1)num[0] = 1：以arr[0]=6结尾的子序列{6}的长度为1
(2)num[1] = 1 : 以arr[1]=4结尾的子序列{4}的长度为1
(3)num[2] = 2 : 以arr[2]=5结尾的子序列{4,5}的长度为2
(4)num[3] = 3 : 以arr[3]=8结尾的子序列{4,5,8}的长度为3
(5)num[4] = 3 : 以arr[4]=7结尾的子序列{4,5,7}的长度为3
(6)num[5] = 1 : 以arr[5]=3结尾的子序列{3}的长度为1
(7)num[6] = 4 : 以arr[6]=9结尾的子序列{4,5,8,9}和{4,5,7,9}的长度为4
(8)也就是说数组arr中任意元素i的num[i]等于它前面的、值比它小的元素j的num[j]的最大值加1，如果它前面没有值比它小的数那么num[i]=1;
即num[i] = max(1,num[j]+1) 其中j< i ,且arr[j] <= arr[i]
java实现
public class Main {
public static void main(String[] args) {
int [] arr = {6,4,5,8,7,3,9};
int[] num = new int[arr.length];
int length = 0;
for(int i = 0;i<num.length;i++){
num[i] = 1;
for(int j =0;j<i;j++){
if(arr[j]<=arr[i]&&Math.max(1,num[j]+1)>num[i]) num[i] = Math.max(1,num[j]+1);
}
if(num[i]>length) length = num[i];
}
System.out.println(length);
}
}
————————————————————————————————————————————————————

https://blog.csdn.net/weixin_34060299/article/details/88001901

• 解决思路：动态规划

1、首先使用邻接矩阵存储无向图

2、将找到结点1到节点N的最短路径分解成结点1到节点i的最短路径（1<i<节点数）

3、对于每一个未计算的结点i，考虑已经计算过的当前最短路径端点choice,如果结点i和结点j直接有边，则计算从结点choice到未计算结点的最短路径

代码不是c++的 但是原理是一样的 搞清楚原理是关键

d[i]=min{A[i][j]+A[j]}

源码

1.  
   import java.util.HashSet;
2.  
   import java.util.Iterator;
3.  
   import java.util.Scanner;
4.  
   import java.lang.Integer;
5.  
   import java.util.Set;
6.  
    
7.  
   public class NoPointerChart {
8.  
   public static void main(String[] args) {
9.  
   Scanner in = new Scanner(System.in);
10.  
    int V = in.nextInt(); //输入点数
11.  
    int E = in.nextInt(); //输入边数
12.  
     
13.  
    int[][] A = new int[V][V];
14.  
     
15.  
    for (int i = 0; i < V; i++) { //初始化所有边为无穷大
16.  
    for (int j = 0; j < V; j++) {
17.  
    A[i][j] = Integer.MAX_VALUE;
18.  
    }
19.  
    }
20.  
    for (int i = 0; i < E; i++) { //输入每一条边
21.  
    int j = in.nextInt();
22.  
    int k = in.nextInt();
23.  
    int v = in.nextInt();
24.  
    A[j - 1][k - 1] = v;
25.  
    A[k - 1][j - 1] = v;
26.  
    }
27.  
     
28.  
    Set<Integer> unVisited = new HashSet<>(V); //记录未访问节点
29.  
    Set<Integer> visitied = new HashSet<>(V); //记录已经访问的节点
30.  
    int[] d = new int[V];
31.  
    for (int i = 1; i < V; i++) { //初始化最优解都为无限大
32.  
    unVisited.add(i);
33.  
    d[i] = Integer.MAX_VALUE;
34.  
    }
35.  
    visitied.add(0);
36.  
    d[0] = 0;
37.  
     
38.  
    int choice = 0; //中间节点下标，每次选出当前结点到所有可达未标记结点的最短路径端点
39.  
    while (unVisited.size() > 0) { //当仍然有未标记结点的时候
40.  
    int tempMin = Integer.MAX_VALUE; //记录从中间节点到所有可达结点中的最小值（最短路径）
41.  
    int tempMinI = -1; //记录最短路径的端点下标
42.  
    Iterator<Integer> iti = unVisited.iterator();
43.  
    while (iti.hasNext()) { //对于所有未标记的结点
44.  
    int i = iti.next();
45.  
    if (A[choice][i] != Integer.MAX_VALUE) { //如果中间结点到此未标记结点有边
46.  
    if(d[i]>A[choice][i] + d[choice]) //计算中间结点到当前结点的最短路径
47.  
    d[i] = A[choice][i] + d[choice];
48.  
    if (d[i] < tempMin) { //计算当前结点到所有可达未标记结点的最短路径
49.  
    tempMin = d[i];
50.  
    tempMinI = i;
51.  
    }
52.  
     
53.  
    }
54.  
    }
55.  
    unVisited.remove(tempMinI);visitied.add(tempMinI); //将当前结点记录未已经标记
56.  
    choice = tempMinI; //重新定位中间结点
57.  
    }
58.  
     
59.  
    System.out.println(d[V-1]);
60.  
    }
61.  
    //测试用例 第一行输入结点数V和边数E ，以下E行输入每条边的端点和权值
62.  
    //6 9
63.  
    //1 2 6
64.  
    //1 3 3
65.  
    //2 3 2
66.  
    //2 4 5
67.  
    //3 4 3
68.  
    //3 5 4
69.  
    //4 5 2
70.  
    //4 6 3
71.  
    //5 6 5
72.  
    }
73.  

—————————————————————————————————————————————————————

 

 

 

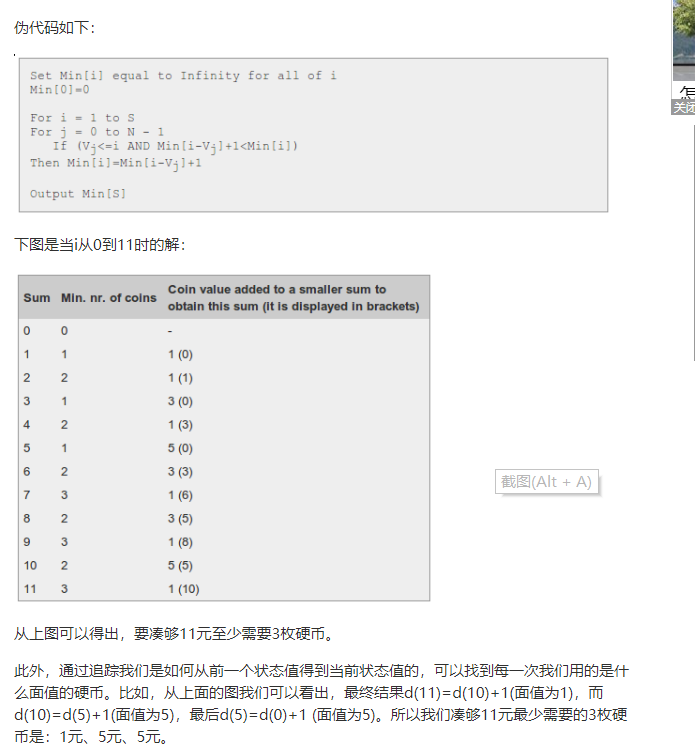
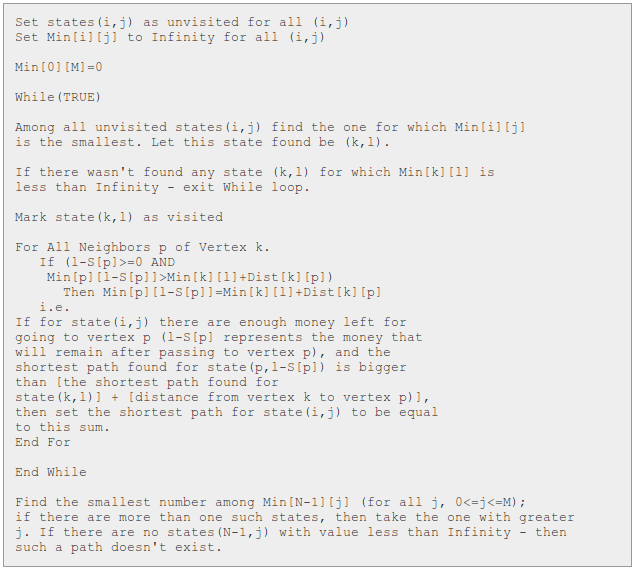
 伪代码如下

 

 

 1-6就是一个二维数组的dp问题了 只不过有一些技巧性 一开始将6边形转换为矩阵的形式 似乎是叫压缩

——————————————————————————————————————————————————————————

 

 

 

 

 ————————————————————————————————————————————————————————————————

 

 

——————————————————————————————————————————————————————————————————————————

上面是对dp大致的理解和介绍

下面是一些题目和代码的练习和参考

 https://www.bilibili.com/video/BV18x411V7fm

第一期

 

第一题

先是用斐波那契数列

我理解到的是

斐波那契有两种方法来求

第一种是从后往前用递归求解 由于重子问题 导致要用数组来实时记录数据 

第二种是从前往后用dp求解 填表式的方法 其实实质有点像递归的数组记录

但是我感觉我对递归和dp的关系有一点理解不到位

我觉得在这题斐波那契数列中

从后往前的求法 似乎是回溯的方法 也可以看作是dp只不过先dp从右到左 再从左到右 都是一个状态向另外一个状态转移 然后要计算最初始的f（0）和f（1）才能对后面的2345等求解就导致了这个题目从右向左来计算的时候自然回回溯

而dp呢 直接是从左向右进行 等于是直接进行回溯的那一个操作 

这么说的话

我们可以把回溯和dp当作两种思想 这两种思想有共同点也有不同点

而递归和迭代这两种东西 只不过是我们的方法 在我们用回溯和dp的基础上用的求解答案的方法 算法这样的概念

或许这才是斐波那契所包含的东西（我暂时理解到的）

也欢迎大佬们指出我的问题这是我的荣幸

 

第二题

在一定时间内去打工 如何赚的钱最多

 

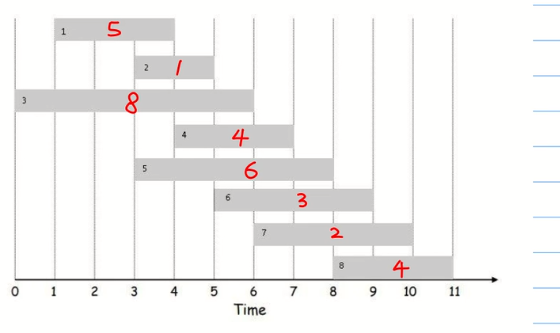
黑字代表工作的项目

红字代表每个项目对应的钱

因为项目之间有冲突 所以在面对一个项目的时候 可以采取选和不选 

实际也就是01背包的问题了

 

 vi表示项目对应的钱

 

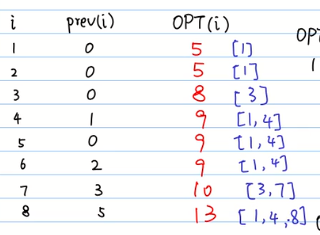
 prev（i）表示选了当前的i以后 还能选前面的最靠近的哪个项目

————————————————————————————————————————

https://www.bilibili.com/video/BV12W411v7rd?from=search&seid=5926982970687044032

第二期

题目一（将用递归和非递归的方式来实现）

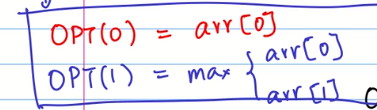
求数组中不相临的元素的和的最大值

 

a[0]+a[2]+a[4]+a[6]=1+4+7+3=15

和上一题一样 同样面临选和不选的情况

总结一下 这种都是相邻的元素之间有冲突不能连续选的时候 

都可以用这种01背包 选和不选

 

 

递归的角度看   出口就有两个   也就是递归的结束条件

 

 

 代码实现

#include<iostream>
using namespace std;
int max(int a, int b) {
if (a > b)return a;
else return b;
}
int rec_opt(int a[],int i) {
if (i == 0)return a[0];
else if (i == 1)return max(a[0], a[1]);
else {
int c = rec_opt(a, i - 2) + a[i];
int d = rec_opt(a, i - 1);
return max(c,d);
}
}
int main() {
int a[7] = { 1,2,4,1,7,8,3 };
int i = 7;
cout<< rec_opt(a,i);
}

 ——————————————————————————————————————

非递归的方法

 

#include<iostream>
using namespace std;
int max(int a, int b) {
if (a > b)return a;
else return b;
}
int dp_opt(int a[],int b[],int n) {
for (int i = 2;i <n;i++) {
int c = b[i-2] + a[i];
int d = b[i-1];
b[i] = max(c, d);
}
return b[n-1];
}

int main() {
int a[7] = { 1,2,4,1,7,8,3 };
int b[7] = { 0xc0c0c0};
int n = 7;
b[0] = a[0];
b[1] = max(a[0], a[1]);
cout << dp_opt(a,b,n) << endl;
}

————————————————————————————————————

第二题 （递归和迭代）

题目的意思大概是用dp然后在一个数组中 每个数字只能用一次 用户输入一个数字

看看输入的这个数字能不能由数组中的数字组成（相加）

内部已经规定了数组大小为6

元素为3,34,4,12,5,2

当然稍微改一下可以变成用户输入一个数组 然后再输入一个数字 看看这个数字能不能由数组中的数字组成（相加）

这里用的dp算法是递归实现的 然后是自后向前的

#include<iostream>
int t = 0;
using namespace std;
int rec_subset(int arr[], int i, int s) {
if (t == 1)return 0;
if (s == 0) { t = 1;return 0; }
else{
if (i == 0){
if (arr[i] == s) { t = 1;return 0; }
else { t = 0;return 0; }
}
else {
rec_subset(arr, i - 1, s);
rec_subset(arr, i - 1, s - arr[i]);
}
}
}
int main() {
int arr[6] = { 3,34,4,12,5,2 };
int i = 5;
int s;
cin >> s;
rec_subset(arr, i, s);
cout << t << endl;
return 0;
}

—————————————————————————————————————————

非递归实现

 用二维数组去记录他的dp的过程

 

 

#include<iostream>

using namespace std;

int max(int a,int b) {
if (a > b)return a;
else return b;
}
int dp_subset(int arr[], int len, int sum)
{
int dp[101][101];
for (int i = 1; i <= len; i++)
dp[0][i] = 0;
dp[0][0] = 1;
for (int i = 1; i <= 6; i++)
for (int j = 0; j <= 13; j++)
{
dp[i][j] = dp[i - 1][j];
if (j >= arr[i])
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - arr[i]]);
//dp【i - 1】[j] || dp【i - 1】【j - data[i】];
}
return dp[len][sum];
}

int main()
{
int data[] = { 0,3,34,4,12,5,2 };
int s;
cin >> s;
cout << dp_subset(data, 6, s);
return 1;
}