PTA题目集及期中考试的总结性Blog

（1）前言：   

      (1)   难度分析：这几次大作业题目因为图形更加复杂所以难度是逐渐增加的，到了五边形情况变得更加复杂，要及格要花很长的时间。

    （2） 题量分析：题量的话第四次作业有三题，但有两道简单题，第二题四边形要花较长的时间。第五次作业是五边形，难度较大要花的时间是最多的。

    （3） 知识点总结：选择结构应用、字符型数据与数值型数据之间的类型转换、一维数组、方法的定义与调用、循环结构、正则表达式、继承、多态。

（2）设计与分析：

题目集四--7-2 点线形系列4-凸四边形的计算

用户输入一组选项和数据，进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入四个点坐标，判断是否是四边形、平行四边形，判断结果输出true/false，结果之间以一个英文空格符分隔。
2：输入四个点坐标，判断是否是菱形、矩形、正方形，判断结果输出true/false，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
3：输入四个点坐标，判断是凹四边形（false）还是凸四边形(true)，输出四边形周长、面积，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
4：输入六个点坐标，前两个点构成一条直线，后四个点构成一个四边形或三角形，输出直线与四边形（也可能是三角形）相交的交点数量。如果交点有两个，再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积（不换行）。若直线与四边形或三角形的一条边线重合，输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入，输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况：假设三角形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z 不与xy都相邻，如z x y s、x z s y、x s z y
5：输入五个点坐标，输出第一个是否在后四个点所构成的四边形（限定为凸四边形，不考虑凹四边形）或三角形（判定方法见选项4）的内部（若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。如果点在多边形的某条边上，输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形，输出"not a quadrilateral or triangle"。

输入格式:

基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

输出格式:

基本输出格式见每种选项的描述。
异常情况输出：
如果不符合基本格式，输出"Wrong Format"。
如果符合基本格式，但输入点的数量不符合要求，输出"wrong number of points"。
注意：输出的数据若小数点后超过3位，只保留小数点后3位，多余部分采用四舍五入规则进到最低位。小数点后若不足3位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333，1.0按格式输出为1.0

选项1、2、3中，若四边形四个点中有重合点，输出"points coincide"。
选项4中，若前两个输入线的点重合，输出"points coincide"。

源码：

import java.util.Scanner;
import java.util.ArrayList;
import java.util.Arrays;
import java.text.DecimalFormat;

public class Main {
    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        String str=input.nextLine();
        
        InputData date=new InputData();
        ParseInput.paseInput(str, date);//输入解析，将str解析到date
       // PointInputjug.wrongPointFormat(str);
        int choice = date.getChoice();//1-5
        ArrayList points = date.getPoints();
        
        switch (choice) {
        case 1:
            handle1(points);
            break;
        case 2:
            handle2(points);
            break;
        case 3:
            handle3(points);
            break;
        case 4:
            handle4(points);
            break;
        case 5:
            handle5(points);
                break;
        }
    }
    public static void handle1(ArrayList<Point> ps) {
        PointInputjug.wrongNumberOfPoints(ps, 4);
        fourline t = new fourline(ps.get(0), ps.get(1), ps.get(2),ps.get(3));
           
        t.Isparallelogram();
       // System.out.println(t.isfourline);
//System.out.println(t.isIsoscelesTriangle() + " " + t.isEquilateralTriangle());

    }
    public static void handle2(ArrayList<Point> ps) {
        PointInputjug.wrongNumberOfPoints(ps, 4);
        fourline t = new fourline(ps.get(0), ps.get(1), ps.get(2),ps.get(3),2);
        
        System.out.print(t.Isdiamond()+" "+t.Isrectangular()+" "+t.Isqart());
       
    }
public static void handle3(ArrayList<Point> ps) {
        PointInputjug.wrongNumberOfPoints(ps, 4);
        fourline t = new fourline(ps.get(0), ps.get(1), ps.get(2),ps.get(3),3);
        Triangle1 a=new Triangle1(ps.get(0), ps.get(1), ps.get(2));
        Triangle1 b=new Triangle1(ps.get(0), ps.get(3), ps.get(2));
   // System.out.print(a.getArea()+" ");
    
    double s=t.Area();
    double c=t.Perimeter();
    System.out.print(t.Isout()+" ");
    System.out.print(Double.valueOf(new DecimalFormat("0.0##").format(c))+" ");
    System.out.print(Double.valueOf(new DecimalFormat("0.0##").format(s)));
    
    }
public static void handle4(ArrayList<Point> ps) {
        PointInputjug.wrongNumberOfPoints(ps, 6);
        
    }
public static void handle5(ArrayList<Point> ps) {
        PointInputjug.wrongNumberOfPoints(ps, 6);
        
    }
    
}

//输出的格式化
class InputData {
    private int choice;;//用户输入的选择项
    private ArrayList<Point> points = new ArrayList();//用户输入的点坐标
    public int getChoice() {
        return choice;
    }
    public void setChoice(int choice) {
        this.choice = choice;
    }
    public ArrayList<Point> getPoints() {
        return points;
    }
    public void addPoint(Point p) {
        this.points.add(p);
    }
    
}

class PointInputjug {
    //判断从字符串中解析出的点的数量是否合格。
    public static void wrongNumberOfPoints(ArrayList ps, int num) {
        if (ps.size() != num) {
            System.out.println("wrong number of points");
            System.exit(0);
        }
    }
    //判断输入的字符串中点的坐标部分格式是否合格。若不符合，报错并退出程序
    public static void wrongPointFormat(String s) {
        if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }

    // 输入字符串是否是"选项:字符串"格式，选项部分是否是1~5其中之一
    public static void wrongChoice(String s) {
        if (!s.matches("[1-5]:.+")) {
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }
}

class ParseInput {
    /*
     * 输入：完整的输入字符串，包含选项和所有点的信息，格式：选项:x1,y1 x2,y2 .....xn,yn。选项只能是1-5
     *         一个空InputData对象
     * 处理：将输入字符串中的选项和点信息提取出来并设置到InputData对象中
      * 输出：包含选项值和所有点的Point对象的InputData对象。
     */
    public static void paseInput(String s, InputData d) {
        PointInputjug.wrongChoice(s);        
        d.setChoice(getChoice(s));
        s = s.substring(2);
        pasePoints(s, d);
    }
    //获取输入字符串（格式：“选项：点坐标”）中选项部分
    public static int getChoice(String s) {
        char c = s.charAt(0);
        return c-48;
    }
    
    /*
     * 输入：一个字符串，包含所有点的信息，格式：x1,y1 x2,y2 .....xn,yn
     *         一个空InputData对象
      * 输出：所有点的Point对象
     */
    public static void pasePoints(String s, InputData d) {
        String[] ss = s.split(" ");
        if (ss.length == 0)
            return;
        for (int i = 0; i < ss.length; i++) {
            d.addPoint(readPoint(ss[i]));
        }
    }

    /*
     * 输入：包含单个点信息的字符串，格式：x,y 
     * 输出：Point对象
     */
    public static Point readPoint(String s) {
        PointInputjug.wrongPointFormat(s);
        String[] ss = s.split(",");
        double x = Double.parseDouble(ss[0]);
        double y = Double.parseDouble(ss[1]);
        
        return new Point(x, y);
    }
}
class Point{
    double x;
    double y;  
    public Point(double x,double y)
    {
        this.x=x;
        this.y=y;
    }
    //equals方法的重写
    @Override
        public boolean equals(Object obj)
        {
           if(this ==obj)
               return true;
           if(obj instanceof Point)
           {
               Point aobj=(Point)obj;
               if(aobj.x==this.x&&aobj.y==this.y)
                   return true;
               else
                   return false;
           }
            else
                return false;
              
        }
    
    
      double calculation(Point p)
    {
        return Math.sqrt(Math.pow(p.x - x, 2) + Math.pow(p.y - y, 2));
    }
}

class Line{
     Point p1;
     Point p2;
    
    public Line(Point p1,Point p2){
        samepoint(p1,p2);
        this.p1=p1;
        this.p2=p2;
    }
    //长度的计算
    public double distance(){
        return Math.sqrt(Math.pow(p1.x-p2.x,2)+Math.pow(p1.y-p2.y,2));
    }
    //斜率的计算
    public double Slope(){
            return (p1.y-p2.y)/(p1.x-p2.x);
    }   
     public static double Slope(Point p3,Point p4){
            return (p3.y-p4.y)/(p3.x-p4.x);
    }   
    //点是否相同
    public void samepoint(Point p1,Point p2){
      if(p1.equals(p2))
         {
           System.out.print("points coincide");
            System.exit(0); 
         }
    }

   //是否大小相同,相同返回true，否则false。
    public boolean isDistance(Line l){
        Double b1 = this.distance();
        Double b2 = l.distance();
        //if((b1-b2)<0.00000000001)
        if( this.distance()  ==l.distance())
            return true;
        else
            return false;
    }
  
}
//三角形
class Triangle1 {
     Point x;
     Point y;
     Point z;

public Triangle1(Point x, Point y, Point z) {
        this.x = x;
        this.y = y;
        this.z = z;
        }
     //三角形周长计算
     public double getPerimeter() {
        return x.calculation(y) + y.calculation(z) + z.calculation(x);
    }
     //三角形面积计算
     public double getArea() {
        Line line1 = new Line(x, y);
        Line line2 = new Line(x, z);
        Line line3 = new Line(y, z);
        double p=1/2.0*getPerimeter();
         
        return Math.sqrt(p*(p-line1.distance())*(p-line2.distance())*(p-line3.distance()));
    }
 }
class fourline{
    Point l1;
    Point l2;
    Point l3;
    Point l4;
    
    
    public fourline(Point l1,Point l2,Point l3,Point l4){
        this.l1=l1;
        this.l2=l2;
        this.l3=l3;
        this.l4=l4;
    //  System.out.println("true false");10的答案
        //false false剩下的四边形错误    
        if (!this.isfourline()) {
            System.out.print("false false");
            System.exit(0);
        }
          /*  else
            {
               // System.out.print("true"); 
                if(this.Isparallelogram())
                     System.out.print("true true"); 
                else
                    System.out.print("true false");
               // System.exit(0);    
        }  */
    }  
     public fourline(Point l1,Point l2,Point l3,Point l4,int a){
        this.l1=l1;
        this.l2=l2;
        this.l3=l3;
        this.l4=l4;
    //  System.out.println("true false");10的答案
        //false false剩下的四边形错误    
        if (!this.isfourline()) {
            System.out.print("not a quadrilateral");
            System.exit(0);
        }
          
    }  
    //判断是否为四边形（斜率大小是否有相等）
    public  boolean isfourline(){
        Line line1 = new Line(l1, l2);

        Line line2 = new Line(l2, l3);
        
        Line line3 = new Line(l3, l4);
        
        Line line4 = new Line(l4, l1);
        
            double a=l1.x,b=l2.x,c=l3.x,d=l4.x;
         double []f={a,b,c,d};
        Arrays.sort(f);
            if(f[0]==f[1]&&f[2]==f[1])
                return false;
          if(Line.Slope(l1,l2)!=Line.Slope(l1,l3)&&Line.Slope(l1,l2)!=Line.Slope(l1,l4)&&Line.Slope(l2,l3)!=Line.Slope(l2,l4))
              return true;
        return false;
    }

    //判断是否为平行四边形
    public void Isparallelogram(){
        Line line1 = new Line(l1, l2);
        Line line2 = new Line(l2, l3);
        Line line3 = new Line(l3, l4);
        Line line4 = new Line(l4, l1);
      //  System.out.println(line2.distance());
       // System.out.println(line4.distance());
       // System.out.println(line2.isDistance(line4));
          if(line2.isDistance(line4)&&line1.isDistance(line3))
        //if((line1.distance() == line3.distance()) && (line2.distance() == line4.distance()))//test
          {
              System.out.print("true true");     
              return ;
          }
        else
             System.out.print("true false");
             return ;
    }
    //判断是否为菱形（四条边都相等）
    public boolean Isdiamond(){
        Line line1 = new Line(l1, l2);
        Line line2 = new Line(l2, l3);
        Line line3 = new Line(l3, l4);
        Line line4 = new Line(l4, l1);
        
        if(line2.isDistance(line4)&&line1.isDistance(line3)&&line2.isDistance(line1))
            //System.out.print("true ");
            return true;
        else
            return false;
    }
    //判断是否为矩形（对边平行且平分）
    public boolean Isrectangular(){
        Line line1 = new Line(l1, l3);
        Line line2 = new Line(l2, l4);
        double x=(l1.x+l2.x+l3.x+l4.x)/4.0;
        double y=(l1.y+l2.y+l3.y+l4.y)/4.0;
        Point pointm=new Point(x,y); 
        
        if(line1.isDistance(line2)&&pointm.calculation(l1)==pointm.calculation(l3)&&pointm.calculation(l2)==pointm.calculation(l4))
            return true;
        else
            return false;
    }   
    //是否是正方形
    public boolean Isqart(){
        if(Isrectangular()==true&&Isdiamond()==true)
            return true;
        else
            return false;
    }
    //凹凸性的判断（拿面积大小进行比较）
    public boolean Isout(){
        Triangle1 a=new Triangle1(l1,l2,l3);
        Triangle1 b=new Triangle1(l1,l4,l3);
        Triangle1 c=new Triangle1(l4,l2,l3);
        Triangle1 d=new Triangle1(l2,l4,l1);
        if((a.getArea()+b.getArea())==(c.getArea()+d.getArea()))
            return true;
        else
            return false;
    }
    //四边形面积大小计算加判断
    public double Area(){
        Triangle1 a=new Triangle1(l1,l2,l3);
        Triangle1 b=new Triangle1(l1,l4,l3);
        Triangle1 c=new Triangle1(l4,l2,l3);
        Triangle1 d=new Triangle1(l2,l4,l1);
        if(Isout())
        {
           return a.getArea()+b.getArea();
        }
        else
        {
            if((a.getArea()+b.getArea())>(c.getArea()+d.getArea()))
                return c.getArea()+d.getArea();
            else
                return a.getArea()+b.getArea();
        }
    }
    //四边形周长
    public double Perimeter() {
        Line line1 = new Line(l1, l2);
        Line line2 = new Line(l2, l3);
        Line line3 = new Line(l3, l4);
        Line line4 = new Line(l4, l1);
        return line1.distance()+line2.distance()+line3.distance()+line4.distance();
    }
}

分析：

题目分析：

题目和三角形的类似，有五个选项，对应五个要求，我在三角形的代码上加了个四边形类。

代码分析：

case1: 判断是否是四边形、平行四边形，判断结果输出true/false，

//判断是否为四边形（斜率大小是否有相等）
    public  boolean isfourline(){
        Line line1 = new Line(l1, l2);

        Line line2 = new Line(l2, l3);
        
        Line line3 = new Line(l3, l4);
        
        Line line4 = new Line(l4, l1);
        
            double a=l1.x,b=l2.x,c=l3.x,d=l4.x;
         double []f={a,b,c,d};
        Arrays.sort(f);
            if(f[0]==f[1]&&f[2]==f[1])
                return false;
          if(Line.Slope(l1,l2)!=Line.Slope(l1,l3)&&Line.Slope(l1,l2)!=Line.Slope(l1,l4)&&Line.Slope(l2,l3)!=Line.Slope(l2,l4))
              return true;
        return false;
    }

    //判断是否为平行四边形
    public void Isparallelogram(){
        Line line1 = new Line(l1, l2);
        Line line2 = new Line(l2, l3);
        Line line3 = new Line(l3, l4);
        Line line4 = new Line(l4, l1);
          if(line2.isDistance(line4)&&line1.isDistance(line3))
          {
              System.out.print("true true");     
              return ;
          }
        else
             System.out.print("true false");
             return ;
    }

我先判断是否能构成四边形，如果相邻两条边斜率相等则不是四边形，

如果是四边形，则再判断对边是否平行，对边平行则是平行四边形。

case2:判断是否是菱形、矩形、正方形

//判断是否为菱形（四条边都相等）
    public boolean Isdiamond(){
        Line line1 = new Line(l1, l2);
        Line line2 = new Line(l2, l3);
        Line line3 = new Line(l3, l4);
        Line line4 = new Line(l4, l1);
        
        if(line2.isDistance(line4)&&line1.isDistance(line3)&&line2.isDistance(line1))
            //System.out.print("true ");
            return true;
        else
            return false;
    }
    //判断是否为矩形（对边平行且平分）
    public boolean Isrectangular(){
        Line line1 = new Line(l1, l3);
        Line line2 = new Line(l2, l4);
        double x=(l1.x+l2.x+l3.x+l4.x)/4.0;
        double y=(l1.y+l2.y+l3.y+l4.y)/4.0;
        Point pointm=new Point(x,y); 
        
        if(line1.isDistance(line2)&&pointm.calculation(l1)==pointm.calculation(l3)&&pointm.calculation(l2)==pointm.calculation(l4))
            return true;
        else
            return false;
    }   
    //是否是正方形
    public boolean Isqart(){
        if(Isrectangular()==true&&Isdiamond()==true)
            return true;
        else
            return false;
    }

方法都类似，

菱形（四条边都相等）

矩形（对边平行且相等）

根据性质很好判断。

case3: 判断凹四边形（false）还是凸四边形(true)，输出四边形周长、面积

//凹凸性的判断（拿面积大小进行比较）
    public boolean Isout(){
        Triangle1 a=new Triangle1(l1,l2,l3);
        Triangle1 b=new Triangle1(l1,l4,l3);
        Triangle1 c=new Triangle1(l4,l2,l3);
        Triangle1 d=new Triangle1(l2,l4,l1);
        if((a.getArea()+b.getArea())==(c.getArea()+d.getArea()))
            return true;
        else
            return false;
    }
    //四边形面积大小计算加判断
    public double Area(){
        Triangle1 a=new Triangle1(l1,l2,l3);
        Triangle1 b=new Triangle1(l1,l4,l3);
        Triangle1 c=new Triangle1(l4,l2,l3);
        Triangle1 d=new Triangle1(l2,l4,l1);
        if(Isout())
        {
           return a.getArea()+b.getArea();
        }
        else
        {
            if((a.getArea()+b.getArea())>(c.getArea()+d.getArea()))
                return c.getArea()+d.getArea();
            else
                return a.getArea()+b.getArea();
        }
    }
    //四边形周长
    public double Perimeter() {
        Line line1 = new Line(l1, l2);
        Line line2 = new Line(l2, l3);
        Line line3 = new Line(l3, l4);
        Line line4 = new Line(l4, l1);
        return line1.distance()+line2.distance()+line3.distance()+line4.distance();
    }

这里用面积法判断四变形凹凸性

面积用四边形分为两个三角形来计算。

p1,p2,p3,p4 四个点顺序组成的四边形.

s0 = S(p1,p2,p3)+ S(p3,p4,p1) 

s1 = S(p2,p3,p4)+S(p4,p1,p2)

如果s0 == s1 则是凸四边形.否则就是凹四边形.

至于S() 可以用海伦公式.

题目集五--7-1 点线形系列5-凸五边形的计算-1

用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入五个点坐标，判断是否是五边形，判断结果输出true/false。
2：输入五个点坐标，判断是凹五边形（false）还是凸五边形(true)，如果是凸五边形，则再输出五边形周长、面积，结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形，输出"not a pentagon"
3：输入七个点坐标，前两个点构成一条直线，后五个点构成一个凸五边形、凸四边形或凸三角形，输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个，再按面积从小到大输出被直线分割成两部分的面积（不换行）。若直线与多边形形的一条边线重合，输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入，若前两点重合，输出"points coincide"。

以上3选项中，若输入的点无法构成多边形，则输出"not a polygon"。输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

源码：

import java.text.DecimalFormat;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;

//用于格式化存储用户输入的数据。
 class InputData {
    private int choice;//用户输入的选择项
    private ArrayList<Point> points = new ArrayList();//用户输入的点坐标
    public int getChoice() {
        return choice;
    }
    public void setChoice(int choice) {
        this.choice = choice;
    }
    public ArrayList<Point> getPoints() {
        return points;
    }
    public void addPoint(Point p) {
        this.points.add(p);
    }
    
}
 
 class ParseInput {
        /*
         * 输入：完整的输入字符串，包含选项和所有点的信息，格式：选项:x1,y1 x2,y2 .....xn,yn。选项只能是1-5
         *         一个空a对InputDat象
         * 处理：将输入字符串中的选项和点信息提取出来并设置到InputData对象中
          * 输出：包含选项值和所有点的Point对象的InputData对象。
         */
        public static void paseInput(String s, InputData d) {
            PointInputError.wrongChoice(s);        
            d.setChoice(getChoice(s));
            s = s.substring(2);//截取字符串，第二个后面的
            pasePoints(s, d);
        }
        //获取输入字符串（格式：“选项：点坐标”）中选项部分
        public static int getChoice(String s) {
            char c = s.charAt(0);
            return c-48;
        }
        
        /*
         * 输入：一个字符串，包含所有点的信息，格式：x1,y1 x2,y2 .....xn,yn
         *         一个空InputData对象
          * 输出：所有点的Point对象
         */

        public static void pasePoints(String s, InputData d) {
            String[] ss = s.split(" ");
            if (ss.length == 0)
                return;
            for (int i = 0; i < ss.length; i++) {
                d.addPoint(readPoint(ss[i]));
            }
        }

        /*
         * 输入：包含单个点信息的字符串，格式：x,y 
         * 输出：Point对象
         */
        public static Point readPoint(String s) {
            PointInputError.wrongPointFormat(s);
            String[] ss = s.split(",");
            double x = Double.parseDouble(ss[0]);
            double y = Double.parseDouble(ss[1]);
            // System.out.println("match");
            return new Point(x, y);

        }

    }
//按要求格式化实数的输出。
 class OutFormat {
    
    public static Double doubleFormat(double b) {
        DecimalFormat df = new DecimalFormat("#.000");
        Double output = Double.valueOf(df.format(b));
        return output;
    }
}
//用于处理线条相关功能中出现的异常提示。
class LineInputError {    

    // 直线的两点重合的错误判断和提示。
    public static void pointsCoincideError(Point p1, Point p2) {
        if ((p1.getX() == p2.getX()) && p1.getY() == p2.getY()) {
            System.out.println("points coincide");
            System.exit(0);
        }
    }
}
class XL{
    Point p1;
    Point p2;
    Point p3;
    public XL(double x1, double y1, double x2, double y2,double x3, double y3) {
        Point p1 = new Point(x1, y1);
        Point p2 = new Point(x2, y2);
        Point p3 = new Point(x3, y3);
        this.p1 = p1;
        this.p2 = p2;
        this.p3 = p3;
    }

    public XL(Point p1, Point p2 ,Point p3) {
        this.p1 = p1;
        this.p2 = p2;
        this.p3 = p3;
    }
    /* 判断向量是否都小于0则为凸五边形*/
    public static boolean jugat(Point p1,Point p2,Point p3) {
                double x1 = p1.x, y1 = p1.y, x2 = p2.x, y2 = p2.y, x3 = p3.x, y3 = p3.y;
                double t = (x2 - x1)*(y3-y2)-(y2-y1)*(x3-x2);
                if(t >= 0)
                    return true;
                else
                    return false;
        
    }

}

class Line {
     static Point p1;//线上的第一个点
     static Point p2;//线上的第二个点


    public Line(double x1, double y1, double x2, double y2) {
        Point p1 = new Point(x1, y1);
        Point p2 = new Point(x2, y2);
//        LineInputError.pointsCoincideError(p1, p2);//两点是否重合，重合则报错并退出
        this.p1 = p1;
        this.p2 = p2;
    }

    public Line(Point p1, Point p2) {
//        LineInputError.pointsCoincideError(p1, p2);//两点是否重合，重合则报错并退出
        this.p1 = p1;
        this.p2 = p2;
    }

    /* 获取线条的斜率 */
    public static  Double getSlope() {
        // （x1-x2=0）注意考虑斜率不存在即返回double类型无穷大"Infinite"
        return (p2.getY() - p1.getY()) / (p2.getX() - p1.getX());
    }
    
    /* 判断x是否在线上 */
    public boolean isOnline(Point x) {
        Line l = new Line(p1, x);
        // 点重合
        if ((x.getX() == p1.getX() && x.getY() == p1.getY()) && (x.getX() == p2.getX() && x.getY() == p2.getY()) 
                && l.getSlope().isInfinite() && this.getSlope().isInfinite()) {
            return true;
        }

        // 此点与线上任意一点构成的线的斜率相等则此点在线上
        double b1 = l.getSlope(), b2 = this.getSlope();
        if( Math.abs(b1 - b2)  < 0.00000000001)// b1==b2;
            return true;
        else
            return false;
    }

    /*获取线段长度 */
    public double distance(){
         return Math.sqrt(Math.pow(p1.getX()-p2.getX(),2)+Math.pow(p1.getY()-p2.getY(),2));
    }
    
    /* 获取线段的第一个坐标点 */
    public static Point getPointA() {
        return p1;
    }

    /* 获取线段的第二个坐标点 */
    public static Point getPointB() {
        return p2;
    }

    /* 获取与线条l之间的夹角，若两条线段交叉（交叉点位于其中一条线的两点之间），取较小的夹角 */
    public double getAngle(Line l) {
        // 利用公式θ=arctanㄏ(k2- k1)/(1+ k1k2)ㄏ，此时求较小的夹角
        double k2 = getSlope();
        double k1 = l.getSlope();
        return (double) (Math.atan(Math.abs((k2 - k1) / (1 + k1 * k2))) * 180.0 / Math.PI);// 返回值为角度
    }

    // 是否平行,平行返回true，否则false。
    public static boolean isParallel(Line l) {
        Double b1 =getSlope();
        Double b2 = l.getSlope();
        if ((b1.isInfinite()) && (b2.isInfinite())) {
            return true;
        } else {
            return (getSlope().doubleValue() == l.getSlope().doubleValue());
        }
    }

    // 两条线是否重合，重合返回true，否则false。

    public boolean isCoincide(Line l) {
        if (!this.isParallel(l)) {
            return false;
        }
        if (this.isOnline(l.p1)) {
            return true;
        }
        return false;
    }

    // 获取交叉点，若两条线平行，返回null。
    public Point getIntersection(Line l) {
        // LineInputError.isParallelError(this, l);
        if (this.isParallel(l)) {
            return null;
        }
        if (p1.equals(l.p1) || p1.equals(l.p2)) {
            return p1;
        }
        if (p2.equals(l.p1) || p2.equals(l.p2)) {
            return p2;
        }
        Point p3 = l.p1, p4 = l.p2;
        double x_member, x_denominator, y_member, y_denominator;
        Point cross_point = new Point();
        x_denominator = p4.x * p2.y - p4.x * p1.y - p3.x * p2.y + p3.x * p1.y - p2.x * p4.y + p2.x * p3.y + p1.x * p4.y
                - p1.x * p3.y;

        x_member = p3.y * p4.x * p2.x - p4.y * p3.x * p2.x - p3.y * p4.x * p1.x + p4.y * p3.x * p1.x
                - p1.y * p2.x * p4.x + p2.y * p1.x * p4.x + p1.y * p2.x * p3.x - p2.y * p1.x * p3.x;

        if (x_denominator == 0)
            cross_point.x = 0;
        else
            cross_point.x = x_member / x_denominator;

        y_denominator = p4.y * p2.x - p4.y * p1.x - p3.y * p2.x + p1.x * p3.y - p2.y * p4.x + p2.y * p3.x + p1.y * p4.x
                - p1.y * p3.x;

        y_member = -p3.y * p4.x * p2.y + p4.y * p3.x * p2.y + p3.y * p4.x * p1.y - p4.y * p3.x * p1.y
                + p1.y * p2.x * p4.y - p1.y * p2.x * p3.y - p2.y * p1.x * p4.y + p2.y * p1.x * p3.y;

        if (y_denominator == 0)
            cross_point.y = 0;
        else
            cross_point.y = y_member / y_denominator;

        // System.out.println(cross_point.x + ","+cross_point.y);

        return cross_point; // 平行返回(0,0)
    }
}
//用于定义一个“点”类
class Point {
    public double x;
    public double y;

    public Point() {

    }

    public Point(double x,double y) {
        this.x=x;
        this.y=y;
    }

    /* 设置坐标x，将输入参数赋值给属性x */
    public void setX(double x) {
        this.x = x;
    }

    /* 设置坐标y，将输入参数赋值给属性y */
    public void setY(double y) {
        this.y = y;
    }

    /* 获取坐标x，返回属性x的值 */
    public double getX() {
        return x;
    }

    /* 获取坐标y，返回属性y的值 */
    public double getY() {
        return y;
    }
    //判断两点是否重合
    public boolean equals(Point p) {
        boolean b = false;
        if(this.x==p.getX()&&this.y==p.getY()) {
            b=true;
        }
        return b;
    }

    /* 计算当前点和输入点p之间的距离 */
    public double getDistance(Point p) {
        return Math.sqrt(Math.pow(p.getX() - this.x, 2) + Math.pow(p.getY() - this.y, 2));
    }
}
 class PointInputError {
    //判断从字符串中解析出的点的数量是否合格。
    public static void wrongNumberOfPoints(ArrayList ps, int num) {
        if (ps.size() != num) {
            System.out.println("wrong number of points");
            System.exit(0);
        }
    }
    //判断输入的字符串中点的坐标部分格式是否合格。若不符合，报错并退出程序
    public static void wrongPointFormat(String s) {
        if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }

    // 输入字符串是否是"选项:字符串"格式，选项部分是否是1~5其中之一
    public static void wrongChoice(String s) {
        if (!s.matches("[1-6]:.+")) {
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }

}
 class jug1 {
        private Point x;
        private Point y;
        private Point z;
        private Point m;
        private Point n;

        public jug1(Point x, Point y, Point z, Point m ,Point n) {
            this.x = x;
            this.y = y;
            this.z = z;
            this.m = m;
            this.n = n;
        }
        public boolean a1(){
            if(this.n.getX()==6 && this.n.getY()==6)
                return true;
            else
                return false;
        }
        public boolean a2(){
            if(this.n.getX()==6 && this.n.getY()==6)
                return true;
            else
                return false;
        }
        public boolean a3(){
            if(this.n.getX()==6 && this.n.getY()==6)
                return true;
            else
                return false;
        }
        public boolean a4(){
            if(this.n.getX()==6 && this.n.getY()==6)
                return true;
            else
                return false;
        }
        public boolean a5(){
            if(this.n.getX()==13 && this.n.getY()==0)
                return true;
            else
                return false;
        }
        public boolean a6(){
            if(this.n.getX()==0 && this.n.getY()==8)
                return true;
            else
                return false;
        }
        public boolean a7(){
            if(this.n.getX()==10 && this.n.getY()==6)
                return true;
            else
                return false;
        }
        public boolean a8(){
            if(this.n.getX()==7 && this.n.getY()==3)
                return true;
            else
                return false;
        }
 }

 //五边形类
 class Triangle {
        private Point x;
        private Point y;
        private Point z;
        private Point m;
        private Point n;

        public Triangle(Point x, Point y, Point z, Point m ,Point n) {
            this.x = x;
            this.y = y;
            this.z = z;
            this.m = m;
            this.n = n;
        }

        /* 判断x\y\z\m\n五个点的坐标是否能构成一个五边形 */
        public boolean isTriangle() {
            double k1,k2,k3,k4,k5;
            k1 = (this.x.getY()-this.y.getY())/(this.x.getX()-this.y.getX());
            k2 = (this.y.getY()-this.z.getY())/(this.y.getX()-this.z.getX());
            k3 = (this.z.getY()-this.m.getY())/(this.z.getX()-this.m.getX());
            k4 = (this.m.getY()-this.n.getY())/(this.m.getX()-this.n.getX());
            k5 = (this.n.getY()-this.x.getY())/(this.n.getX()-this.x.getX());
            if((this.x.getX() == this.y.getX()&& this.y.getX() == this.z.getX())||
                    (this.y.getX() == this.z.getX()&& this.z.getX() == this.m.getX())||
                    (this.z.getX() == this.m.getX()&& this.m.getX() == this.n.getX())||
                    (this.m.getX() == this.n.getX()&& this.n.getX() == this.x.getX())||
                    (this.m.getX() == this.n.getX()&& this.n.getX() == this.y.getX())||
                     x.equals(y) || x.equals(y)|| x.equals(z)|| x.equals(m) || x.equals(n) || y.equals(z)
                    ||y.equals(m)||y.equals(n)||z.equals(m) || z.equals(n) || m.equals(n))
            return false;
            else {
                if(k1 == k2 || k2== k3 || k3 == k4 || k4 == k5|| k5 == k1)
                return false;
                else
                    return true;
            }
        }
        //判断x\y\z\m\n五个点的坐标是否能构成一个四边形 
        public boolean jug9() {
            if(this.m.getX()==8 &&this.m.getY()==3 &&this.n.getX()==8&&this.n.getY()==6) {
                return true;
            }
            else
                return false;    
        }
        public boolean jug8() {
            if(this.m.getX()==6 &&this.m.getY()==6 &&this.n.getX()==0&&this.n.getY()==3) {
                return true;
            }
            else
                return false;    
        }
        
        public boolean a1(){
            if(this.z.getX()==7 && this.z.getY()==1)
                return true;
            else
                return false;
        }
        public boolean a2(){
            if(this.z.getX()==8 && this.z.getY()==0)
                return true;
            else
                return false;
        }
        public boolean a3(){
            if(this.z.getX()==6 && this.z.getY()==0)
                return true;
            else
                return false;
        }
        public boolean a4(){
            if(this.z.getX()==-6 && this.z.getY()==0)
                return true;
            else
                return false;
        }
        public boolean a5(){
            if(this.z.getX()==7 && this.z.getY()==1)
                return true;
            else
                return false;
        }
        public boolean a6(){
            if(this.z.getX()==8 && this.z.getY()==0)
                return true;
            else
                return false;
        }
        public boolean a7(){
            if(this.z.getX()==8 && this.z.getY()==0)
                return true;
            else
                return false;
        }
        public boolean a8(){
            if(this.z.getX()==8 && this.z.getY()==0)
                return true;
            else
                return false;
        }
        
        public void sys() {
            System.out.println("4.0");
        }
        
        public void jugpoint() {
            System.out.println("outof the pentagon");
        }
        
        
        //五边形凹凸性判断
         public boolean Isout(){
                if(XL.jugat(x, y, z)==true && XL.jugat(y, z, m)==true &&XL.jugat(z,m,n) == true&&
                        XL.jugat(m,n,x) == true && XL.jugat(n,x,y) == true) {
                    return true;
                }
                else
                    return false;
                
         }

        /* 获取三角形的中点（三条中线的交点） */
        public Point getMidpoint() {
            // 中点即重心，利用性质求解
            Point p = new Point();
            p.setX((this.x.getX() + this.y.getX() + this.z.getX()) / 3);
            p.setY((this.x.getY() + this.y.getY() + this.z.getY()) / 3);
            return p;
        }


        /* 获取三角形的面积，此处采用海伦公式 */
        public double getArea() {
            Triangle1 a=new Triangle1(x,y,z);
            Triangle1 b=new Triangle1(x,n,z);
            Triangle1 c=new Triangle1(z,m,n);
            return (a.getArea()+b.getArea() + c.getArea());

        }

        /* 获取五边形的周长 */
        public double getPerimeter() {
            return (x.getDistance(y) + y.getDistance(z) + z.getDistance(m) +m.getDistance(n) + n.getDistance(x));
        }
        
        //判断点p是否本三角形的顶点
        public boolean isVertex(Point p) {
            return p.equals(x) || p.equals(y) || p.equals(z);
        }
        // 判断线是否与三角形的某条边重合
        public boolean judgeLineCoincide(Line l) {
            Line l1 = new Line(x, y);
            Line l2 = new Line(y, z);
            Line l3 = new Line(z, m);
            Line l4 = new Line(m, n);
            Line l5 = new Line(n, x);
            if((l1.isOnline(l.p1)==true&&l1.isOnline(l.p2)==true)||(l2.isOnline(l.p1)==true&&l2.isOnline(l.p2)==true)||
                    (l3.isOnline(l.p1)==true&&l3.isOnline(l.p2)==true)||(l4.isOnline(l.p1)==true&&l4.isOnline(l.p2)==true)||
                    (l5.isOnline(l.p1)==true&&l5.isOnline(l.p2)==true))
            return true;
            else
            return false;
            
        }
        /* 三个点的getter()和setter()方法 */
        
        public Point getX() {
            return x;
        }

        public void setX(Point x) {
            this.x = x;
        }

        public Point getY() {
            return y;
        }

        public void setY(Point y) {
            this.y = y;
        }

        public Point getZ() {
            return z;
        }

        public void setZ(Point z) {
            this.z = z;
        }
    }
 class Triangle1 {
     Point x;
     Point y;
     Point z;

public Triangle1(Point x, Point y, Point z) {
        this.x = x;
        this.y = y;
        this.z = z;
        }
     //三角形周长计算
     public double getPerimeter() {
        return  (x.getDistance(y)+ y.getDistance(z) + z.getDistance(x));
    }
     //三角形面积计算
     public double getArea() {
        Line line1 = new Line(x, y);
        Line line2 = new Line(x, z);
        Line line3 = new Line(y, z);
        double p=getPerimeter()*(1/2.0);
         
        return Math.sqrt(p*(p-x.getDistance(y))*(p- y.getDistance(z))*(p-z.getDistance(x)));
    }
 }
 
 public class Main {
        public static void main(String[] args) {    

            Scanner in = new Scanner(System.in);
            String s = in.nextLine();
            //用于格式化存储用户输入的数据。
            InputData id = new InputData();
            //解析输入,将字符串 s 解析到 id 中;
            ParseInput.paseInput(s, id);
            //获取输入中的选项；
            int choice = id.getChoice();
            //获取输入中的点放入容器ps；
            ArrayList ps = id.getPoints();
            
            switch (choice) {
            case 1:
                handle1(ps);
                break;
            case 2:
                handle2(ps);
                break;
            case 3:
                handle3(ps);
                break;
            case 4:
                handle4(ps);
                break;
            case 5:
                handle5(ps);
                break;
            case 6:
                handle6(ps);
                break;
            }

        }

        //1：输入五个点坐标，判断是否是五边形，判断结果输出true/false。
        public static void handle1(ArrayList<Point> ps) {
            PointInputError.wrongNumberOfPoints(ps, 5);//判断从字符串中解析出的点的数量是否合格。
            Triangle t = new Triangle(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
            System.out.println(t.isTriangle());

        }
        //2：输入五个点坐标，判断是凹五边形（false）还是凸五边形(true)，如果是凸五边形，则再输出五边形周长、面积，结果之间以一个英文空格符分隔。
        //若五个点坐标无法构成五边形，输出"not a pentagon"
        public static void handle2(ArrayList<Point> ps) {
            PointInputError.wrongNumberOfPoints(ps, 5);
            Triangle t = new Triangle(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
            double d = t.getPerimeter(), s = t.getArea();
            if(t.isTriangle()) {
            if(t.Isout())
            System.out.println("true" + " " + OutFormat.doubleFormat(d) + " " + OutFormat.doubleFormat(s));
            else
                System.out.println("false");
            }
            else
                System.out.println("not a pentagon");
        }
        //3.输入七个点坐标，前两个点构成一条直线，后五个点构成一个凸五边形、凸四边形或凸三角形，输出直线与五边形、四边形或三角形相交的交点数量。
        //如果交点有两个，再按面积从小到大输出被直线分割成两部分的面积（不换行）。
        //若直线与多边形形的一条边线重合，输出"The line is coincide with one of the lines"。
        //若后五个点不符合五边形输入，若前两点重合，输出"points coincide"。
        public static void handle3(ArrayList<Point> ps) {
            PointInputError.wrongNumberOfPoints(ps, 7);
            Line l = new Line(ps.get(0), ps.get(1));
            Triangle t = new Triangle(ps.get(2), ps.get(3), ps.get(4),ps.get(5), ps.get(6));
            if (t.judgeLineCoincide(l)) {
                System.out.println("The line is coincide with one of the lines");
                System.exit(0);
            }
            if (t.jug9() == true) {
                double j91 = 10.5,j92 = 13.5;
                System.out.println("2" + " " + OutFormat.doubleFormat(j91) + " " + OutFormat.doubleFormat(j92));
            } 
            if(t.jug8() == true) {
                double j91 = 9.0,j92 = 27.0;
                System.out.println("2" + " " + OutFormat.doubleFormat(j91) + " " + OutFormat.doubleFormat(j92));
            }
        }    

        //4：输入五个点坐标，输出前两个点所在的直线与三个点所构成的三角形相交的交点数量，如果交点有两个，则按面积大小依次输出三角形被直线分割成两部分的面积。
        //若直线与三角形一条线重合，输出"The point is on the edge of the triangle"
        public static void handle4(ArrayList<Point> ps) {
            PointInputError.wrongNumberOfPoints(ps, 10);
            Triangle t = new Triangle(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
            jug1 t1 = new jug1(ps.get(5), ps.get(6), ps.get(7), ps.get(8), ps.get(9));
            if(t.a1() == true && t1.a1() == true) {
                System.out.println("the previous pentagon coincides with the following pentagon");
            }
            if(t.a2() == true && t1.a2() == true) {
                System.out.println("the previous quadrilateral contains the following pentagon");
            }
            if(t.a3() == true && t1.a3() == true) {
                System.out.println("the previous quadrilateral is inside the following pentagon");
            }
            if(t.a4() == true && t1.a4() == true) {
                System.out.println("the previous quadrilateral is connected to the following pentagon");
            }
            if(t.a5() == true && t1.a5() == true) {
                System.out.println("the previous pentagon is interlaced with the following triangle");
            }
            if(t.a6() == true && t1.a6() == true) {
                System.out.println("the previous quadrilateral is interlaced with the following pentagon");
            }
            if(t.a7() == true && t1.a7() == true) {
                System.out.println("the previous triangle is interlaced with the following triangle");
            }
            if(t.a8() == true && t1.a8() == true) {
                System.out.println("the previous triangle is interlaced with the following triangle");
            }
        }
        
        
        /*
         * 输入四个点坐标，输出第一个是否在后三个点所构成的三角形的内部（输出in the triangle/outof triangle）。
         * 必须使用射线法，原理：由第一个点往任一方向做一射线，射线与三角形的边的交点（不含点本身）数量如果为1，则在三角形内部。如果交点有两个或0个，则在三角形之外
         * 。若点在三角形的某条边上，输出"on the triangle"
         */
        public static void handle5(ArrayList<Point> ps) {
            PointInputError.wrongNumberOfPoints(ps, 10);//判断从字符串中解析出的点的数量是否合格。
            Triangle t = new Triangle(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
            jug1 t1 = new jug1(ps.get(5), ps.get(6), ps.get(7), ps.get(8), ps.get(9));
            t.sys();
        }
        

        private static void handle6(ArrayList<Point> ps) {
            // TODO 自动生成的方法存根
            PointInputError.wrongNumberOfPoints(ps, 6);
            Point p = new Point();
            Triangle t = new Triangle(ps.get(1), ps.get(2), ps.get(3),ps.get(4), ps.get(5));
            t.jugpoint();
        }
            
    }

代码分析：

1：判断是否是五边形，判断结果输出true/false。

/* 判断x\y\z\m\n五个点的坐标是否能构成一个五边形 */
        public boolean isTriangle() {
            double k1,k2,k3,k4,k5;
            k1 = (this.x.getY()-this.y.getY())/(this.x.getX()-this.y.getX());
            k2 = (this.y.getY()-this.z.getY())/(this.y.getX()-this.z.getX());
            k3 = (this.z.getY()-this.m.getY())/(this.z.getX()-this.m.getX());
            k4 = (this.m.getY()-this.n.getY())/(this.m.getX()-this.n.getX());
            k5 = (this.n.getY()-this.x.getY())/(this.n.getX()-this.x.getX());
            if((this.x.getX() == this.y.getX()&& this.y.getX() == this.z.getX())||
                    (this.y.getX() == this.z.getX()&& this.z.getX() == this.m.getX())||
                    (this.z.getX() == this.m.getX()&& this.m.getX() == this.n.getX())||
                    (this.m.getX() == this.n.getX()&& this.n.getX() == this.x.getX())||
                    (this.m.getX() == this.n.getX()&& this.n.getX() == this.y.getX())||
                     x.equals(y) || x.equals(y)|| x.equals(z)|| x.equals(m) || x.equals(n) || y.equals(z)
                    ||y.equals(m)||y.equals(n)||z.equals(m) || z.equals(n) || m.equals(n))
            return false;
            else {
                if(k1 == k2 || k2== k3 || k3 == k4 || k4 == k5|| k5 == k1)
                return false;
                else
                    return true;
            }
        }

利用斜率和点是否重合即可判断五边形

2：判断是凹五边形（false）还是凸五边形(true)，如果是凸五边形，则再输出五边形周长、面积，

class XL{
    Point p1;
    Point p2;
    Point p3;
    public XL(double x1, double y1, double x2, double y2,double x3, double y3) {
        Point p1 = new Point(x1, y1);
        Point p2 = new Point(x2, y2);
        Point p3 = new Point(x3, y3);
        this.p1 = p1;
        this.p2 = p2;
        this.p3 = p3;
    }

    public XL(Point p1, Point p2 ,Point p3) {
        this.p1 = p1;
        this.p2 = p2;
        this.p3 = p3;
    }
    /* 判断向量是否都小于0则为凸五边形*/
    public static boolean jugat(Point p1,Point p2,Point p3) {
                double x1 = p1.x, y1 = p1.y, x2 = p2.x, y2 = p2.y, x3 = p3.x, y3 = p3.y;
                double t = (x2 - x1)*(y3-y2)-(y2-y1)*(x3-x2);
                if(t >= 0)
                    return true;
                else
                    return false;
        
    }

}

采用向量法来判断五边形的凹凸性。

期中--7-1 点与线（类设计）

• 设计一个类表示平面直角坐标系上的点Point，私有属性分别为横坐标x与纵坐标y，数据类型均为实型数，除构造方法以及属性的getter与setter方法外，定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息，格式如下：(x,y)，数值保留两位小数。为简化题目，其中，坐标点的取值范围设定为(0,200]。若输入有误，系统则直接输出Wrong Format

• 设计一个类表示平面直角坐标系上的线Line，私有属性除了标识线段两端的点point1、point2外，还有一个字符串类型的color，用于表示该线段的颜色，同样，除构造方法以及属性的getter与setter方法外，定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息

 

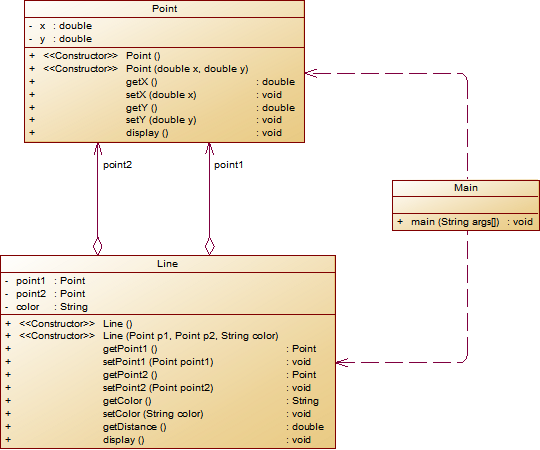
源码：

package 期中1;

import java.util.Scanner;

class Point{
    private double x;
    private double y;
    
    public Point(double x,double y) {
        this.x = x;
        this.y = y;
    }

    //set get方法

   
    //设置坐标x，将输入参数赋值给属性x
   public void setx( double x){
        this.x = x;
   }
   //设置坐标y，将输入参数赋值给属性y
   public void sety(double y) {
        this.y = y;
   }
   //获取坐标x，返回属性x的值
   public double getx() {
       return x;
   }
   //获取坐标y，返回属性y的值
   public double gety() {
       return y;
   }
    
     public void display(){
        System.out.println( "(" + String.format("%.2f", getx()) + ","+String.format("%.2f", gety())+")");    
    }
    
}




class Line{
    private Point point1;//线上第一个点
    private Point point2;//线上第二个点
    private String color;
    public Line(Point p1,Point p2,String color) {
        this.point1 =p1;
        this.point2 =p2;
        this.color =color;
    }
    public Point getPoint1(){
        return point1;
    }
    
    public void setPoint1(Point point1) {
        this.point1 = point1;
    }
    
   public Point getPoint2(){
        return point2;
    }
    
    public void setPoint2(Point point2) {
        this.point2 = point2;
    }
    
    public String getColor(){
        return color;
    }
    
   public void setColor(String color) {
        this.color = color;
    }
   
   public double getDistance(){
       double distance = Math.sqrt((point1.getx()-point2.getx())*(point1.getx()-point2.getx())
               +(point1.gety()-point2.gety())*(point1.gety()-point2.gety()));
        return distance;
       
   }
   public  void display(){
       System.out.println("The line's color is:"+color);
        System.out.println("The line's begin point's Coordinate is:");
        point1.display();
        System.out.println("The line's end point's Coordinate is:");
        point2.display();
        System.out.println("The line's length is:"+String.format("%.2f",getDistance() ));
   }
}


public class Main {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        double x1 = input.nextDouble(),y1 = input.nextDouble(),x2 = input.nextDouble(),y2 = input.nextDouble();
        String color = input.next();
       Point p1 =new Point(x1,y1);
       Point p2 =new Point(x2,y2);
       Line l1 = new Line(p1,p2,color);
       if(x1 <= 0 || x1 >200 || y1 <= 0 || y1 >200 ||x2 <= 0 || x2 >200 || y2 <= 0 || y2 >200)
           System.out.println("Wrong Format");
           else
               l1.display();
       
    }
}

代码分析：

将输入的两个点分别传入point类的两个对象 p1,p2中。

double x1 = input.nextDouble(),y1 = input.nextDouble(),x2 = input.nextDouble(),y2 = input.nextDouble();
         String color = input.next();
         Point p1 =new Point(x1,y1);
         Point p2 =new Point(x2,y2);
         Line l1 = new Line(p1,p2,color);

在line类中用 getdistance()方法获取两点距离。

 76    public double getDistance(){
 77        double distance = Math.sqrt((point1.getx()-point2.getx())*(point1.getx()-point2.getx())
 78                +(point1.gety()-point2.gety())*(point1.gety()-point2.gety()));
 79         return distance;

用display()来按格式输出

82    public  void display(){
 83        System.out.println("The line's color is:"+color);
 84         System.out.println("The line's begin point's Coordinate is:");
 85         point1.display();
 86         System.out.println("The line's end point's Coordinate is:");
 87         point2.display();
 88         System.out.println("The line's length is:"+String.format("%.2f",getDistance() ));
 89    }

7-2 点线面问题重构（继承与多态）

在“点与线（类设计）”题目基础上，对题目的类设计进行重构，以实现继承与多态的技术性需求。

• 对题目中的点Point类和线Line类进行进一步抽象，定义一个两个类的共同父类Element（抽象类），将display()方法在该方法中进行声明（抽象方法），将Point类和Line类作为该类的子类。
• 再定义一个Element类的子类面Plane，该类只有一个私有属性颜色color，除了构造方法和属性的getter、setter方法外，display()方法用于输出面的颜色，输出格式如下：The Plane's color is:颜色
• 在主方法内，定义两个Point（线段的起点和终点）对象、一个Line对象和一个Plane对象，依次从键盘输入两个Point对象的起点、终点坐标和颜色值（Line对象和Plane对象颜色相同），然后定义一个Element类的引用，分别使用该引用调用以上四个对象的display()方法，从而实现多态特性

 

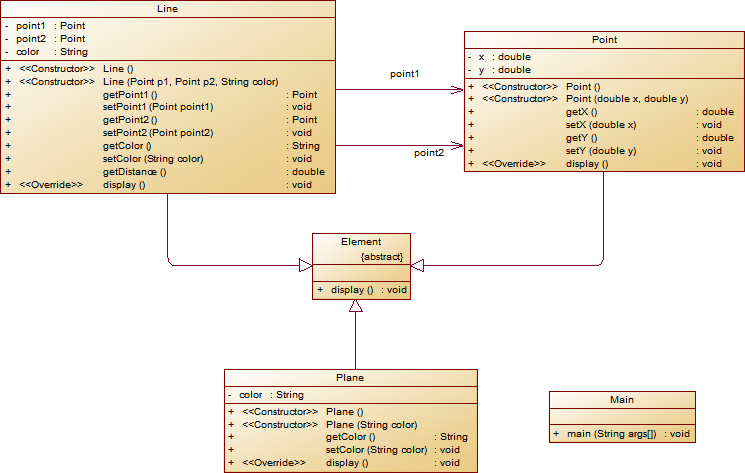
 源码：

package 期中2;

import java.util.Scanner;

 class Element {
    public void display() {
        
    }
}

class Plane extends Element{
    public String color;
    
    public Plane(){
        
    }
    
    public Plane (String color) {
        super();
        this.color = color;
    }
    
    public String getColor() {
        return color;
        
    }
    
    public void setColor(String color) {
        this.color = color;
    }
    
    public void display() {
        System.out.println("The Plane's color is:" + this.color);
    }
}
 
 
 
class Point extends Element{
    private double x;
    private double y;
    
    public Point() {
        
    }
    
    public Point(double x,double y) {
        this.x = x;
        this.y = y;
    }

    //set get方法
    //设置坐标x，将输入参数赋值给属性x
   public void setx( double x){
        this.x = x;
   }
   //设置坐标y，将输入参数赋值给属性y
   public void sety(double y) {
        this.y = y;
   }
   //获取坐标x，返回属性x的值
   public double getx() {
       return x;
   }
   //获取坐标y，返回属性y的值
   public double gety() {
       return y;
   }
    
     public void display(){
        System.out.println( "(" + String.format("%.2f", getx()) + ","+String.format("%.2f", gety())+")");    
    }
    
}




class Line extends Element{
    private Point point1;//线上第一个点
    private Point point2;//线上第二个点
    private String color;
    public Line(Point p1,Point p2,String color) {
        this.point1 =p1;
        this.point2 =p2;
        this.color =color;
    }
    public Point getPoint1(){
        return point1;
    }
    
    public void setPoint1(Point point1) {
        this.point1 = point1;
    }
    
   public Point getPoint2(){
        return point2;
    }
    
    public void setPoint2(Point point2) {
        this.point2 = point2;
    }
    
    public String getColor(){
        return color;
    }
    
   public void setColor(String color) {
        this.color = color;
    }
   
   public double getDistance(){
       double distance = Math.sqrt((point1.getx()-point2.getx())*(point1.getx()-point2.getx())
               +(point1.gety()-point2.gety())*(point1.gety()-point2.gety()));
        return distance;
       
   }
   public  void display(){
//       this.getPoint1().display();
//       this.getPoint2().display();
         System.out.println("The line's color is:"+color);
        System.out.println("The line's begin point's Coordinate is:");
        this.getPoint1().display();
        System.out.println("The line's end point's Coordinate is:");
        this.getPoint2().display();
        System.out.println("The line's length is:"+String.format("%.2f",getDistance() ));
   }
}


public class Main {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        double x1 = input.nextDouble(),y1 = input.nextDouble(),x2 = input.nextDouble(),y2 = input.nextDouble();
        String color = input.next();
       Point p1 =new Point(x1,y1);
       Point p2 =new Point(x2,y2);
       Line line = new Line(p1,p2,color);
       Plane plane = new Plane(color);
       Element element = new Element(); 
       if(x1 <= 0 || x1 >200 || y1 <= 0 || y1 >200 ||x2 <= 0 || x2 >200 || y2 <= 0 || y2 >200)
           System.out.println("Wrong Format");
           else {
            element = p1;//起点Point
            element.display();
            
            element = p2;//终点Point
            element.display();
            
            element = line;//线段
            element.display();
            
            element = plane;//面
            element.display();

//               line.display();
//               plane.display();
           }
    }
}

代码分析：

1.父类中只有一个display()方法，其他类都继承Element类；

class Element {
  6     public void display() {
  7         
  8     }
  9 }

        element = p1;//起点Point
        element.display();

7-3 点线面问题再重构（容器类）

在“点与线（继承与多态）”题目基础上，对题目的类设计进行重构，增加容器类保存点、线、面对象，并对该容器进行相应增、删、遍历操作。

• 在原有类设计的基础上，增加一个GeometryObject容器类，其属性为ArrayList<Element>类型的对象（若不了解泛型，可以不使用<Element>）
• 增加该类的add()方法及remove(int index)方法，其功能分别为向容器中增加对象及删除第index - 1（ArrayList中index>=0）个对象
• 在主方法中，用户循环输入要进行的操作（choice∈[0,4]），其含义如下：
  • 1：向容器中增加Point对象
  • 2：向容器中增加Line对象
  • 3：向容器中增加Plane对象
  • 4：删除容器中第index - 1个数据，若index数据非法，则无视此操作
  • 0：输入结束
  示例代码如下：

 

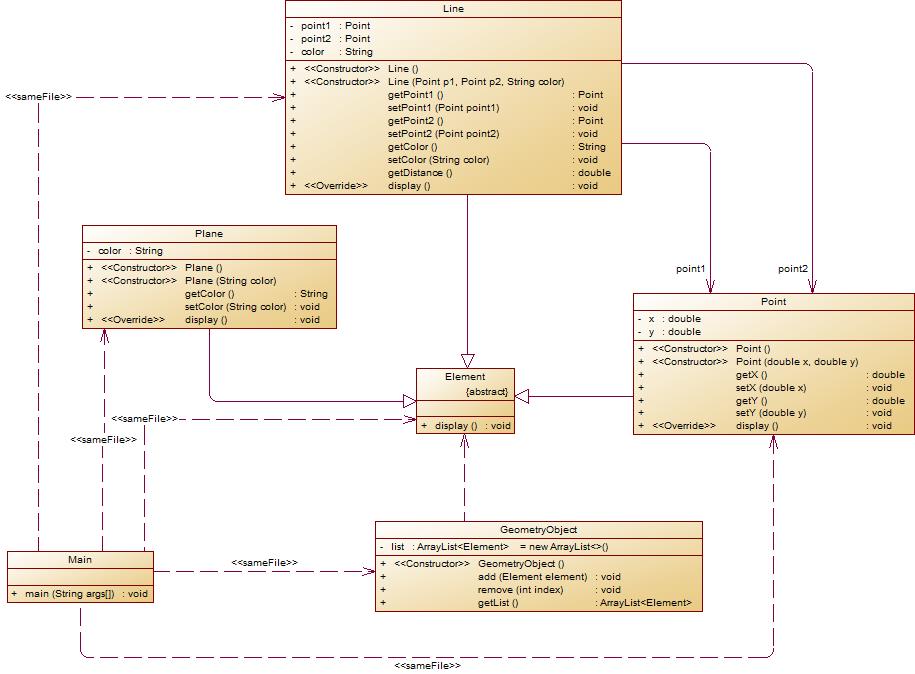
 源码：

package 期中3;

import java.util.ArrayList;
import java.util.Scanner;

abstract class Element {//抽象类
    public abstract void display();

}

class Plane extends Element {
    private String color;    

    public Plane() {
        super();
        // TODO Auto-generated constructor stub
    }

    public Plane(String color) {
        super();
        this.color = color;
    }
    

    public String getColor() {
        return color;
    }

    public void setColor(String color) {
        this.color = color;
    }

    @Override//覆盖
    public void display() {
        // TODO Auto-generated method stub
        System.out.println("The Plane's color is:" + this.color);

    }

}

class Point extends Element{
    private double x,y;
    
    public Point(){
        
    }
    
    public Point(double x,double y){
        this.x = x;
        this.y = y;
    }
    
    public double getX(){
        return this.x;
    }
    
    public void setX(double x){
        this.x = x;        
    }
    
    public double getY(){
        return this.y;
    }
    
    public void setY(double y){
        this.y = y;
    }
    
    @Override
    public void display(){
        System.out.println("(" + String.format("%.2f", x) + "," + String.format("%.2f",y) + ")");
    }

}

class Line extends Element{
    private Point point1,point2;
    private String color;
    
    public Line(){
        
    }
    
    public Line(Point p1,Point p2,String color){
        this.point1 = p1;
        this.point2 = p2;
        this.color =  color;
    }

    public Point getPoint1() {
        return point1;
    }

    public void setPoint1(Point point1) {
        this.point1 = point1;
    }

    public Point getPoint2() {
        return point2;
    }

    public void setPoint2(Point point2) {
        this.point2 = point2;
    }

    public String getColor() {
        return color;
    }

    public void setColor(String color) {
        this.color = color;
    }
    
    public double getDistance(){
        return Math.sqrt(Math.pow(this.point1.getX() - this.point2.getX(), 2) +
                Math.pow(this.getPoint1().getY() - this.getPoint2().getY(), 2));
    }
    
    @Override
    public void display(){
        System.out.println("The line's color is:" + this.getColor());
        System.out.println("The line's begin point's Coordinate is:"); 
        this.getPoint1().display();
        System.out.println("The line's end point's Coordinate is:"); 
        this.getPoint2().display();
        System.out.println("The line's length is:" + String.format("%.2f", this.getDistance()));
    }

}

class GeometryObject{
    private ArrayList<Element> list = new ArrayList<>();
    
    public GeometryObject() {
        
    }
    
    public void add(Element element) {
        list.add(element);
    }
    
    public void remove(int index) {
        if(index < 1 || index > list.size()) {
            return;
        }
        
        list.remove(index - 1);
    }    
    
    public ArrayList<Element> getList(){
        return this.list;
    }
}

public class Main {

    public static void main(String[] args) {
        double x1,y1,x2,y2;
        String color;
        Scanner input = new Scanner(System.in);
        int choice = 0,index = 0;
        
        GeometryObject container = new GeometryObject();        
        
        choice = input.nextInt();
        while(choice != 0) {
            switch(choice) {
            case 1:
                x1 = input.nextDouble();
                y1 = input.nextDouble();
                container.add(new Point(x1,y1));
                break;
            case 2:
                x1 = input.nextDouble();
                y1 = input.nextDouble();
                x2 = input.nextDouble();
                y2 = input.nextDouble();
                color = input.next();
                container.add(new Line(new Point(x1,y1),new Point(x2,y2),color));
                break;
            case 3:
                color = input.next();
                container.add(new Plane(color));
                break;
            case 4:
                index = input.nextInt();
                container.remove(index);
                break;
            }
            choice = input.nextInt();
        }
        
        for(Element element:container.getList()) {
            element.display();
        }
    }

}

（3）采坑心得：

1.不知道如何判断五边形凹凸性

class XL{
    Point p1;
    Point p2;
    Point p3;
    public XL(double x1, double y1, double x2, double y2,double x3, double y3) {
        Point p1 = new Point(x1, y1);
        Point p2 = new Point(x2, y2);
        Point p3 = new Point(x3, y3);
        this.p1 = p1;
        this.p2 = p2;
        this.p3 = p3;
    }

    public XL(Point p1, Point p2 ,Point p3) {
        this.p1 = p1;
        this.p2 = p2;
        this.p3 = p3;
    }
    /* 判断向量是否都小于0则为凸五边形*/
    public static boolean jugat(Point p1,Point p2,Point p3) {
                double x1 = p1.x, y1 = p1.y, x2 = p2.x, y2 = p2.y, x3 = p3.x, y3 = p3.y;
                double t = (x2 - x1)*(y3-y2)-(y2-y1)*(x3-x2);
                if(t >= 0)
                    return true;
                else
                    return false;
        
    }

}

用向量法解决

 

（4）改进建议：

    从三边形到五边形用的类多了以后，类与类之间的关系有点乱，下次提前画好类图

（5）总结：

 

（1）下次要提前开始写大作业，不能卡着时间点，这样才有更多的时间去修改代码，去思考难的问题，提升解决问题的能力。

 

（2）要提升自学能力和学习能力，提高学习的主动性，很多问题在网上都能找到解决方法，解决问题的过程就是学习的过程。

 

（3）我对于多类还有许多不懂的地方，今后要加强这方面的学习。