数据结构基础温故而知新(一)——线性表
基本概念：
什么是程序？
算法+数据结构=程序
数据和数据元素
数据时所有能被输入到计算机中，且能被计算机处理的符号（数字、字符等）的集合，它是计算机操作对象的总称。
数据元素是数据（集合）中的一个“个体”，在计算机中通常作为一个整体进行考虑和处理，是数据结构中讨论的“基本单位”。
两类数据元素
一类是不可分割的“原子”型数据元素，整数5，字符“N”等
另一类是由多个款项构成的数据元素，其中每个款项被称为一个“数据项”。
关键字与数据对象
关键字指的是能识别一个或多个数据元素的数据项。若能起唯一识别作用，则称之为“主”关键字，否则称之为“次”关键字。
数据对象是具有相同特性的数据元素的集合。它是数据的一个子集。
什么是数据结构？
数据结构是一堆数据元素和这些数据元素之间的关系的总和。
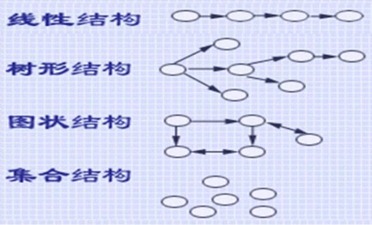
分类：线性结构、树形结构、图形结构、集合结构
数据结构的两个方面
逻辑结构 物理结构
什么是算法？
算法是对问题求解过程的一种描述，是为解决一个或一类问题给出的一个确定的有限长的操作序列。
算法的五个特征：有穷性 确定性 可行性 输入 输出
算法的评价标准
正确性 可读性 健壮性 时间与空间效率
线性表的顺序存储
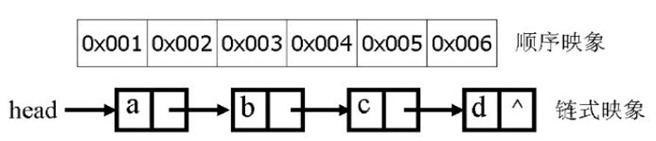
线性表的顺序存储是指用一组地址连续的存储单元依次存储线性表中的数据元素，从而使得逻辑上相邻的两个元素在物理位置上也相邻。在这种存储方式下，元素间的逻辑关系无须占用额外的空间来存储。
一般地，以LOC(ai)表示线性表中第一个元素的存储位置，在顺序存储结构中，第i个元素ai的存储位置为
LOC(ai)=LOC(ai)+(i-1)×L
其中，L是表中每个元素所占空间的大小。根据该计算关系，可以随机存取表中的任一个元素。
线性表采用顺序存储结构的优点是可以随机取表中的元素，缺点是插入和删除操作需要移动元素。插入元素前要移动元素以挪出空的存储单元，然后再插入元素；删除元素时同样需要移动元素，以填充被删除的元素空出来的存储单元。
在表长为n的线性表中插入新元素时，共有n+1个插入位置，在位置1（元素ai所在位置）插入新元素，表中原有的n个元素都需要移动，在位置n+1（元素an所在位置之后）插入新元素时不需要移动任何元素，因此，等概率下（即新元素在n+1个位置插入的概率相同时）插入一个新元素需要移动元素的个数Einsert
![clip_image002[7]](http://images.cnblogs.com/cnblogs_com/luoht/201107/201107091134197887.gif "clip_image002[7]"){kind=small}
其中，Pi表示在表中的位置i插入新元素的概率。
在表长为n的线性表中删除元素时，共有n个可删除的元素，删除元素a1时需要移动n-1个元素，删除元素an时不需要移动元素，因此，等概率下删除元素时需要移动元素的个数Edelete为
![clip_image002[5]](http://images.cnblogs.com/cnblogs_com/luoht/201107/201107091134208660.gif "clip_image002[5]"){kind=small}
其中，qi表示删除元素ai的概率
线性表的链式存储
线性表的链式存储是用节点来存储数据元素，基本的节点结构：数据域+指针域
其中，数据域用于存储数据元素的值，指针域则存储当前元素的直接前驱或直接后继信息，指针域中的信息称为指针（或链）。
存储各数据元素的节点的地址并不要求是连续的，因此存储数据元素的同时必须存储元素之间的逻辑关系。另外，节点空间只有在需要的时候才申请，无须事先分配。
节点之间通过指针域构成一个链表，若节点中只有一个指针域，则称为线性链表（或单链表）。
在链式存储结构中，只需要一个指针（称为头指针）指向第一个节点，就可以顺序访问到表中的任意一个元素。
在链表存储结构下进行插入和删除，其实质都是对相关指针的修改。
单链表节点类型定义
typedef struct node
{
int data; /*节点的数据域，此处假设为整型*/
struct node *link; /*节点的指针域 */
}NODE,*LinkList;
单链表查找操作
//在表中查找第k个元素，若找到，返回该元素节点的指针；否则，返回空指针NULL
LinkList Find_List(LinkList L,int k)
{
LinkList p;
int i;
i=1; //初始时，令p指向第一个元素节点，i为计数器
p=L->link;
while(p&&i<k) //顺时针链向后查找，直到p指向第k个元素节点或p指向空
{
p=p->link;
i++;
}
if(p&&i==k) //存在第k个元素且指针p指向该元素节点
return p;
return NULL; //第k个元素不存在
}
单链表插入操作
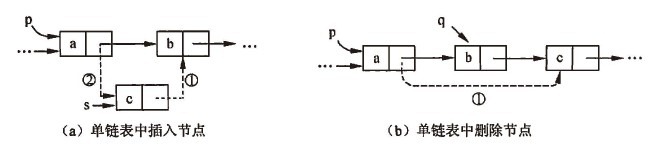
在单链表中，若在P所指节点后插入新元素节点（s所指节点，已经生成），其基本步骤如下。
1. s->link=p->link;
2. p->link=s;
即先将p所指节点的后继节点指针赋给s所指节点的指针域，然后将p所指节点的指针域修改为指向s所指节点。
//将元素newelem插入表中第k个元素之前，若成功则返回0；否则返回-1，
//该插入操作等同于将元素newelem插入在第k-1个元素之后
int Insert_List(LinkList L,int k,int newelem)
{
LinkList p,s;
if(k==1)
{
p=L;
}
else
{
p=Find_List(L,k-1);
}
if(!p) return -1;
s=(NODE*)malloc(sizeof(NODE));
if(!s) return -1;
s->data=newelem;
s->link=p->link;
p->link=s;
return 0;
}
单链表删除操作
同理，在单链表中删除p所指节点的后继节点时，步骤如下。
1． q=p->link;
2． P->link=p->link->link;
3． Free(q);
即先令临时指针q指向待删除的节点，然后修改p所指节点的指针域为指向p所指节点的后继的后继节点， 从而将元素b所在的节点从链表中删除，最后释放q所指节点的空间。
线性表采用链式表作为存储结构时，不能对数据元素进行随机访问，但是插入和删除操作不需要移动元素。
//删除表中的第k个元素节点，若成功返回0，否则返回-1
//删除第k个元素，相当于令第k-1个元素节点的指针域指向第k-1个元素所在节点
int Delete_List(LinkList L,int k)
{
LinkList p,q;
if(k==1) p=L;
else
p=Find_List(L,k-1);
if(!p||p->link) return -1;
q=p->link;
p->link=q->link;
free(q);
return 0;
}
根据节点中指针域的设置方式，还有其他几种链表结构。
双向链表。每个节点包含两个指针，分别指出当前节点元素的直接前驱和直接后继。其特点是可从表中任意的元素节点出发，从两个方向上遍历链表。
循环链表。在单向链表（或双向链表的基础上），令表尾节点的指针指向表中的第一个节点，构成循环链表。其特点是可从表中任意节点开始遍历整个链表。
静态链表。借助数组来描述线性表的链式存储结构。
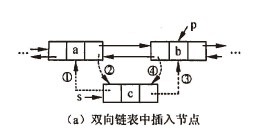
若双向链表中节点的front和next指针域分别指示当前节点的直接前驱和直接后继，双向链表中插入节点*s时指针的变化情况如图所示，其操作过程可表示为：
1.s->front=p->front;
2.p->front->next=s;或者表示为s->front->next=s;
3.s->next=p;
4.p->front=s;
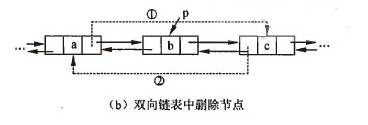
在双向链表中删除节点时指针的变化情况如图，其操作过程可表示为：
1.p->front->next=p->next;
2.p->next->front=p->front;
附：C#描述
class Program
{
static void Main(string[] args)
{
ListClass lc = new ListClass();
ListNode head = new ListNode(1);
lc.InsertNode(head, 0, 1);
lc.InsertNode(head, 1, 2);
lc.InsertNode(head, 2, 3);
lc.InsertNode(head, 3, 4);
lc.InsertNode(head, 4, 5);
lc.InsertNode(head, 5, 6);
lc.InsertNode(head, 6, 7);
lc.InsertNode(head, 4, 8);
Console.WriteLine("数据添加到链表末尾成功！");
ListNode p = new ListNode();
p = head;
while (p != null)
{
Console.WriteLine("链表的当前值为：" + p.Value.ToString());
p = p.NextNode;
}
lc.DeleteNode(head, 3);
Console.WriteLine();
Console.WriteLine("删除节点第4个节点后：");
p = head;
while (p != null)
{
Console.WriteLine("链表的当前值为：" + p.Value.ToString());
p = p.NextNode;
}
Console.ReadLine();
}
}
/// <summary>
/// 节点定义
/// </summary>
class ListNode
{
public ListNode NextNode = null;
public int Value;
public ListNode()
{
}
public ListNode(int NewValue)
{
Value = NewValue;
}
}
/// <summary>
/// 节点操作
/// </summary>
class ListClass
{
/// <summary>
/// 插入节点
/// </summary>
/// <param name="head"></param>
/// <param name="k"></param>
/// <param name="value"></param>
/// <returns></returns>
public int InsertNode(ListNode head, int k, int value)
{
ListNode p, s;
if (k == 0)
{
p = head;
return 0;
}
if (k == 1)
{
s = new ListNode(value);
head.NextNode = s;
return 0;
}
else
{
p = FindNode(head, k - 1);
}
if (p == null)
return -1;
s = new ListNode(value);
s.NextNode = p.NextNode;
p.NextNode = s;
return 0;
}
/// <summary>
/// 查找节点
/// </summary>
/// <param name="head"></param>
/// <param name="k"></param>
/// <returns></returns>
public ListNode FindNode(ListNode head, int k)
{
int i = 0;
ListNode p = new ListNode();
p = head;
while (p != null && i < k)
{
p = p.NextNode;
i++;
}
if (p != null && (i == k))
return p;
return null;
}
/// <summary>
/// 删除节点
/// </summary>
/// <param name="head"></param>
/// <param name="k"></param>
/// <returns></returns>
public int DeleteNode(ListNode head, int k)
{
ListNode p, q;
if (k == 0)
{
p = head;
}
else
{
p = FindNode(head, k - 1);
}
if (p == null || p.NextNode == null)
{
return -1;
}
q = p.NextNode;
p.NextNode = q.NextNode;
return 0;
}
}
浙公网安备 33010602011771号