题解:P2632 Explorer
下文用 \(l_1,l_2\) 代指两条直线。
Part1:解析式计算
已知 \((x_a,y_a),(x_b,y_b)\) 是 \(l_1\) 上的点。
那么易得 \(l_1:y=\dfrac{y_b-y_a}{x_b-x_a}x+\dfrac{x_by_a-x_ay_b}{x_b-x_a}\)。
同理 \(l_2:y=\dfrac{y_d-y_c}{x_d-x_c}x+\dfrac{x_dy_c-x_cy_d}{x_d-x_c}\)。
Part2:考虑暴力
我们还没有想到怎么做。
于是写个 0 分暴力。
对于同一直线上的点,连接最近的点即可。
对于不同直线上的点,暂不考虑,直接暴力连接。
\(O(n+m+nm)\),肯定过不了。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e4+10;
struct edge{
int u,v;
double w;
friend bool operator<(edge aa,edge bb){
return aa.w<bb.w;
}
};
int n,m;
vector<edge> G;
struct DSU{
int fa[maxn];
void reset(){
for(int i=1;i<maxn;i++)fa[i]=i;
}
int find(int x){
if(fa[x]==x)return x;
return fa[x]=find(fa[x]);
}
void merge(int x,int y){
int fx=find(x),fy=find(y);
fa[fx]=fy;
}
DSU(){reset();}
}d;
double kruskal(){
sort(G.begin(),G.end());
int tot=0;
double val=0;
for(auto i:G){
if(d.find(i.u)!=d.find(i.v)){
d.merge(i.u,i.v);
tot++;
val+=i.w;
}
if(tot==n+m-1){
return val;
}
}
}
struct dot{double x,y;};
double dis(dot aa,dot bb){return sqrt((aa.x-bb.x)*(aa.x-bb.x)+(aa.y-bb.y)*(aa.y-bb.y));}
vector<dot> la,lb;
struct node{
double x,y,t;
friend bool operator<(node aa,node bb){return aa.t<bb.t;}
};
vector<node> ea,eb;
int main(){
cin>>n>>m;
int xa,ya,xb,yb,xc,yc,xd,yd;
cin>>xa>>ya>>xb>>yb>>xc>>yc>>xd>>yd;
for(int i=1;i<=n;i++){
double t;
cin>>t;
ea.push_back({t*xa+(1.0-t)*xb,t*ya+(1.0-t)*yb,t});
}
for(int i=1;i<=m;i++){
double t;
cin>>t;
eb.push_back({t*xc+(1.0-t)*xd,t*yc+(1.0-t)*yd,t});
}
sort(ea.begin(),ea.end());
sort(eb.begin(),eb.end());
for(int i=0;i<ea.size();i++){
for(int j=0;j<eb.size();j++){
G.push_back({i,j+n,dis({ea[i].x,ea[i].y},{eb[j].x,eb[j].y})});
}
}
for(int i=0;i<ea.size()-1;i++){
G.push_back({i,i+1,dis({ea[i].x,ea[i].y},{ea[i+1].x,ea[i+1].y})});
}
for(int i=0;i<eb.size()-1;i++){
G.push_back({i+n,i+n+1,dis({eb[i].x,eb[i].y},{eb[i+1].x,eb[i+1].y})});
}
printf("%0.3lf",kruskal());
return 0;
}
Part3:优化
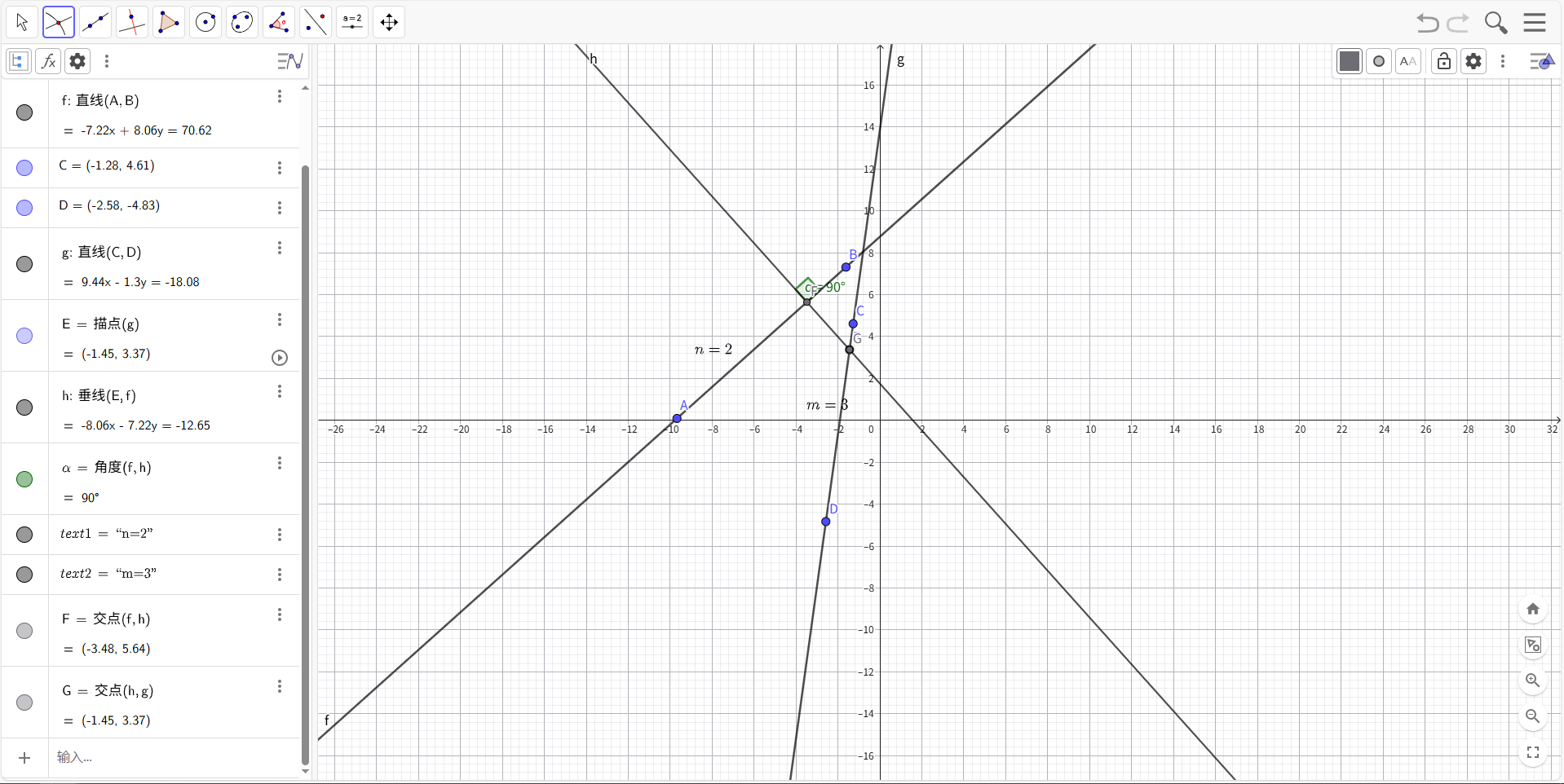
同样地,\(l_2\) 上的点也应该连接到 \(l_1\) 上最近的点。
作垂即可。
\(AG=\sqrt{FG^2+AF^2},BG=\sqrt{FG^2+BF^2}\)。
由于 \(AF>BF\),所以 \(AG>BG\)。
因此对于一个点,我们只需要找到直线上距离垂足最近的点,并与当前点连接即可。
这样边的个数为 \(O(n+m)\)。
本部分建议有兴趣的读者使用 MathDF 完成。
比如我们要过 \(G(x_g,\dfrac{y_d-y_c}{x_d-x_c}x_g+\dfrac{x_dy_c-x_cy_d}{x_d-x_c})\) 作 \(l_1\) 的垂线 \(GF\)。
\(GF: y=-\dfrac{x_b-x_a}{y_b-y_a}x+\left[\left( \dfrac{y_d-y_c}{x_d-x_c}+\dfrac{x_b-x_a}{y_b-y_a}\right)x_g+\dfrac{x_dy_c-x_cy_d}{x_d-x_c}\right]\)
设交点 \(F(x_f,y_f)\)。
\[\begin{cases}
y_f=\dfrac{y_b-y_a}{x_b-x_a}x_f+\dfrac{x_by_a-x_ay_b}{x_b-x_a}\\
\\
y_f=-\dfrac{x_b-x_a}{y_b-y_a}x_f+\left[\left( \dfrac{y_d-y_c}{x_d-x_c}+\dfrac{x_b-x_a}{y_b-y_a}\right)x_g+\dfrac{x_dy_c-x_cy_d}{x_d-x_c}\right]
\end{cases}\]
解得:
\[\begin{cases} x_f = \dfrac{ \big[ x_g (y_b - y_a)(y_d - y_c) + x_g (x_b - x_a)(x_d - x_c) + (y_b - y_a)(x_d y_c - x_c y_d) \big](x_b - x_a) - (y_b - y_a)(x_b y_a - x_a y_b)(x_d - x_c) }{(x_d - x_c)\left[ (y_b - y_a)^2 + (x_b - x_a)^2 \right]}\\
y_f = \dfrac{y_b - y_a}{x_b - x_a} \cdot x_f + \dfrac{x_b y_a - x_a y_b}{x_b - x_a}\end{cases}\]
#include<bits/stdc++.h>
#define ly1(x) (k1*x+b1)
#define ly2(x) (k2*x+b2)
using namespace std;
const int maxn=4e5+10;
struct edge{
int u,v;
double w;
friend bool operator<(edge aa,edge bb){
return aa.w<bb.w;
}
};
int n,m;
vector<edge> G;
struct DSU{
int fa[maxn];
void reset(){
for(int i=1;i<maxn;i++)fa[i]=i;
}
int find(int x){
if(fa[x]==x)return x;
return fa[x]=find(fa[x]);
}
void merge(int x,int y){
int fx=find(x),fy=find(y);
fa[fx]=fy;
}
DSU(){reset();}
}d;
double kruskal(){
sort(G.begin(),G.end());
int tot=0;
double val=0;
for(auto i:G){
if(d.find(i.u)!=d.find(i.v)){
d.merge(i.u,i.v);
tot++;
val+=i.w;
}
if(tot==n+m-1){
return val;
}
}
return 0.0;
}
struct dot{double x,y;};
double dis(dot aa,dot bb){return sqrt((aa.x-bb.x)*(aa.x-bb.x)+(aa.y-bb.y)*(aa.y-bb.y));}
double dis(double x1,double y1,double x2,double y2){return dis({x1,y1},{x2,y2});}
vector<dot> la,lb;
struct node{
double x,y,t;
friend bool operator<(node aa,node bb){return aa.t<bb.t;}
};
vector<node> ea,eb;
vector<pair<double,int>> l1x,l2x;
double k1,k2,b1,b2;
double xa,ya,xb,yb,xc,yc,xd,yd;
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
cin>>xa>>ya>>xb>>yb>>xc>>yc>>xd>>yd;
for(int i=1;i<=n;i++){
double t;
cin>>t;
ea.push_back({t*xa+(1.0-t)*xb,t*ya+(1.0-t)*yb,t});
}
for(int i=1;i<=m;i++){
double t;
cin>>t;
eb.push_back({t*xc+(1.0-t)*xd,t*yc+(1.0-t)*yd,t});
}
if(xb-xa>1e-5)k1=(yb-ya)/(xb-xa)*1.0;else k1=1e18;
if(xd-xc>1e-5)k2=(yd-yc)/(xd-xc)*1.0;else k2=1e18;
b1=(xb*ya-xa*yb)/(xb-xa);
b2=(xd*yc-xc*yd)/(xd-xc);
sort(ea.begin(),ea.end());
sort(eb.begin(),eb.end());
for(int i=0;i<ea.size();i++)l1x.push_back({ea[i].x,i});
for(int i=0;i<eb.size();i++)l2x.push_back({eb[i].x,i});
for(int i=0;i<ea.size()-1;i++){
G.push_back({i,i+1,dis({ea[i].x,ea[i].y},{ea[i+1].x,ea[i+1].y})});
}
for(int i=0;i<eb.size()-1;i++){
G.push_back({i+n,i+n+1,dis({eb[i].x,eb[i].y},{eb[i+1].x,eb[i+1].y})});
}
#define L1 l1x.begin(),l1x.end()
#define L2 l2x.begin(),l2x.end()
sort(L1);sort(L2);
#define mp(x,y) make_pair(x,y)
for(int i=0;i<m;i++){//l2
double xg=eb[i].x,yg=eb[i].y;
double czx=((xg*(yb-ya)*(yd-yc)+xg*(xb-xa)*(xd-xc)+(yb-ya)*(xd*yc-xc*yd))*(xb-xa)-(yb-ya)*(xb*ya-xa*yb)*(xd-xc))/((xd-xc)*((yb-ya)*(yb-ya)+(xb-xa)*(xb-xa)));//套公式这一块
int id=lower_bound(L1,mp(czx,-1))-l1x.begin();
for(int d=-1;d<=1;d++){//也看它左边和右边的哪个近,不过直接全部连接更好
int id2=id+d;//delta id
if((0<=id2&&id2<n)){//isid
id2=l1x[id2].second;//点的id
G.push_back({i+n,id2,dis(xg,yg,ea[id2].x,ea[id2].y)});
}
}
}
for(int i=0;i<n;i++){//l1
double xg=ea[i].x,yg=ea[i].y;
double czx=((xg*(yd-yc)*(yb-ya)+xg*(xd-xc)*(xb-xa)+(yd-yc)*(xb*ya-xa*yb))*(xd-xc)-(yd-yc)*(xd*yc-xc*yd)*(xb-xa))/((xb-xa)*((yb-ya)*(yb-ya)+(xb-xa)*(xb-xa)));
int id=lower_bound(L2,mp(czx,-1))-l2x.begin();
for(int d=-1;d<=1;d++){
int id2=id+d;//delta id
if((0<=id2&&id2<m)){//isid
id2=l2x[id2].second;//点的id
G.push_back({i,id2+n,dis(xg,yg,eb[id2].x,eb[id2].y)});
}
}
}
printf("%0.3lf",kruskal());
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号